Нечаев Моделирование процессов ядерной технологии 2007

3. СТАЦИОНАРНОЕ СОСТОЯНИЕ. КРАЕВЫЕ ЗАДАЧИ

3.1. Стационарныйтеплообменводнослойнойстенке

Стационарное состояние процессов теплопереноса в неподвижной среде. Решение уравнения теплопроводности для одного слоя с учетом зависимости коэффициента теплопроводности от температуры.

Рассмотрим простейший с математической точки зрения случай тепловой задачи – стационарную теплопередачу через одну стенку толщиной s, причем заданы значения температуры на ее обеих сторонах. Строгое задание температур бывает оправдано, например, тем, что более высокая температура – это та, что необходима для проведения технологического процесса, и она задается как необходимое условие; наименьшая температура часто определяется условиями мощного теплосьема, например потоком воды с определенной температурой. В математической физике такие задачи называются задачами с граничным условием I рода, когда считается заданным значение самой искомой функции на внешней границе тела. По физическому смыслу граничные условия первого рода часто называют условиями с источником бесконечной мощности на поверхности тела – потеря всей субстанции (тепла, вещества, количества движения и т.п. за счет ухода в глубь тела) мгновенно компенсируется некоторыми внешними силами.

Практическая задача, соответствующая рассматриваемому случаю, может быть сформулирована так: определить мощность нагревателя для обеспечения требуемой температуры в муфельной электропечи с водоохлаждаемым кожухом.

Построим физическую, и, одновременно, математическую модели нашего теплового устройства. Постоянство температуры во времени – стационарность задачи – означает, что мощность нагревателя равна тепловым потерям через стенки печи за счет теплопроводности. Следовательно, наше явление в целом описывается законом Фурье (2.1.1). Для простоты рассмотрим одномерный вариант – потери тепла только через одну стенку единичной площади. Тогда, с учетом зависимости коэффициента теплопроводности от температуры, закон Фурье запишется:

31

q = – (b + kT)·(dT/dx).

(3.1.1)

Температура внутри печи (при х = 0) строго задана – определена техническим заданием и равна Т1. Следовательно, здесь по опреде-

лению выполняется граничное условие первого рода:
Т|х = о = Т1.	(3.1.2)

Кожух печи охлаждается потоком воды, температура которого Т2 известна и незначительно меняется при прохождении через наше устройство. Т.е., будем считать, что и на второй границе выполня-

ется граничное условие первого рода:
Т|х = s = Т2.	(3.1.3)

Система уравнений (3.1.1) – (3.1.3) является математической моделью поставленной задачи о стационарном потоке тепла в однослойной стенке. Для ее решения разделим переменные в (3.1.1) и, используя (3.1.2), (3.1.3), запишем определенные интегралы:

s	T2
∫ q dx = − ∫(b + k T )dT .		(3.1.4)
0	T1

Из условия сохранения энергии тепло нигде не рождается внут-

ри тела – если только там не идут химические реакции – в ста-

ционарном состоянии поток постоянен на всем пути от 0 до s. Тогда, после выполнения интегрирования, получаем формулу для

расчета величины потока тепла:

q·s = –b·(T2 – T1) – 0.5·k·(T22 – T12) , q = b·(T1 – T2)/s + 0.5·k·(T12 – T22)/s .

Для построения графика зависимости Т(x) внутри слоя перепишем (3.1.4) в виде интегралов-параметров как функций верхнего предела:

x	T
∫qdx =	∫(b + k T )dT ,
0	T1

откуда после интегрирования получаем неявную функцию Т(x):

q·х = -b·(T – T1) –	0.5·k·(T2 – T12),
линейная часть	квадратичное отклонение

из которой легко получить явную функцию x(T):

x = [(bT1+0.5·kT12) – bT – 0.5·kT2]/q, (3.1.5)

которая есть уравнение квадратичной параболы. Из математического анализа известно, что если k > 0, то парабола расположена ветвями вниз, если k < 0 – ветвями вверх. Отсюда следует картина,

32

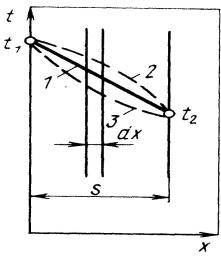
показанная на рис. 2.3.1, иллюстрирующая вогнутости кривых x(T) для разных знаков при k.

Рис. 2.3.1. Стационарное распределение температуры водиночном плоском слое:

1 – теплопроводность не зависит от температуры (k = 0 );

2 – k > 0; 3 – k < 0

На практике, в прикладных расчетах, обычно вычисляют поток при постоянном значении λ, равном среднему значению коэффициента теплопроводности, которое вычисляют при среднем значении температуры в слое. Покажем это теоретически.

Поскольку λ − линейная функция температуры, то, согласно определению среднеарифметического, имеем:

_		1		T		1		T
λ =				∫2λ(T )dT =				∫2(b + k T )dT		= b+k·(T1+T2)/2.
	T	−T			T	−T
	1		2 T		1		2 T
				1				1
Или, что и требовалось доказать:
								_	_	(3.1.6)
								λ = λ(T )

Здесь и далее черта над буквой означает ее среднее значение, в соответствии с принятой в теоретической физике символике.

33

3.2. Многослойнаястенка. Граничноеусловие1-города

Устройство муфельной печи. Многослойная стенка с граничным условием первого рода. Математическая модель и алгоритм решения.

Рассмотрим теперь более сложный, но очень распространенный случай многослойной теплоизолирующей стенки. Такие стенки делают практически у всех нагревательных муфельных печей, устройство которых схематично показано на рис 3.2.1.

1

2

3

4

5

Рис. 3.2.1. Принципиальная схема трубчатой муфельной печи: 1 - муфель; 2 - нагреватель вкерамике; 3 - слой огнеупорного материала; 4 - слои теплоизоляционного материала; 5 - кожух

В печах рассматриваемого типа технологическую камеру образует муфель, выполненный из химически и термостойких материалов. Часто муфелем установки является кварцевая труба. Использование трубы (реактора), изготовленной из высокочистого кварца, исключает загрязнение материала от стенок аппаратуры при их непосредственном контакте или через газовую среду. Поэтому в муфелях подобного типа материал может помещаться в открытом контейнере, если нет технологической необходимости защиты нагреваемого образца от воздействия атмосферного воздуха, или нужно создать регулируемое давление пара одного из компонентов

34

(например, при синтезе и направленной кристаллизации разлагающихся соединений). В таких случаях процессы часто осуществляют в откачанной и запаянной кварцевой ампуле, помещенной в технологическую тепловую зону. Кварц обладает очень малой газопроницаемостью даже при высоких температурах, поэтому в кварцевом муфеле можно проводить процессы в токе водорода или инертного газа. Если муфель изготовлен из огнеупорного, но газопроницаемого материала, например корунда (SiC) или алунда (Al2O3), то часто обрабатываемый термически материал помещают в кварцевую ампулу.

Поверх муфеля располагается резистивный нагреватель. Выделяемая им теплота распространяется не только внутрь образуемой реактором технологической камеры, но и стремится распространиться в противоположном направлении – в окружающее муфель пространство. Поэтому поверх нагревателя необходимо располагать материалы, препятствующие этому явлению, т.е. уменьшить тепловые потери. Так как температура нагревателя и вблизи его, определяемая технологическими параметрами процесса, обычно высока, то поверх нагревателя располагается слой огнеупорного материала, выдерживающего высокие температуры. Однако их высокая теплопроводность вынуждает, для уменьшения тепловых потерь, поверх слоя огнеупорного материала укладывать один или несколько слоев материалов с низкой теплопроводностью (теплоизоляционных материалов). Несколько слоев из разных материалов используются из экономических соображений – обычно более низкотемпературные материалы более дешевы и одновременно более эффективны как теплоизоляторы.

Вся описанная выше система муфеля, нагревателя, огнеупорных и теплоизоляционных материалов помещается в металлический кожух. Кожух может быть водооохлаждаемым или охлаждаемым воздухом. Водяное охлаждение более интенсивно, дает более низкие температуры кожуха – они практически равны температуре охлаждающей воды (граничное условие 1-го рода), и тем самым обеспечивает более комфортные условия работы. Воздушное охлаждение менее эффективно (граничное условие 3-го рода), дает более высокие температуры кожуха, но поэтому обеспечивает меньшие теплопотери и большую экономическую эффективность.

Сначала для упрощения математической задачи примем, что заданы обе температуры – на внутренней стенке муфеля и на кожухе печи. Т.е., будем рассматривать первую краевую задачу математической физики.

35

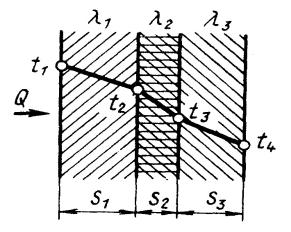
На рис. 3.2.2 показан вариант теплообмена в трехслойной стенке. В общем случае каждый слой имеет свою толщину Si, площадь внешней поверхности Fi, и коэффициент теплопроводности λi. В каждом из N слоев можем записать уравнение для стационарной теплопроводности через всю стенку:

Qi = – λi ·dT/dx·Fi(x) (i = 1,2,..N), (3.2.1)

где Qi – полный поток через всю стенку реальной площадью Fi.

Рис. 3.2.2. Схематическое изображение стационарного состояния теплообмена в трехслойной стенке

Если принять значения теплопроводности и сечения слоя не зависящими от температуры и координаты, и считать их равными среднеарифметическим величинам, то интегрирование дает:

_

Q =

Fi

λ

i (Ti−1 −Ti )

(i =1,2,......N ) ,

_

si

Ti−1 −Ti

Fi−1 − Fi

где

λi = λ(

);

F

=

2

2

иТi – температура на внешней границе i-го слоя. Введем теперь понятие теплового сопротивления:

(3.2.2)

(3.2.3)

Ri (Ti ) =			si			(3.2.5)
		λ	i	F	i

и учтем, что в стационарном состоянии в силу закона сохранения энергии потоки тепловой энергии Qi во всех слоях равны между

36

собой и имеют некоторое значение Q. Это дает возможность переписать систему (3.2.2) в виде:

Ti-1 – Ti = Q·Ri (i = 1,2,…N). (3.2.6)

Уравнений в системе (3.2.6) равно N – числу слоев. Неизвестных величин в ней тоже N, а именно: N-1 значений температур на промежуточных границах плюс 1 (одно) значение потока. Просуммировав (3.2.6) по всем слоям, т.е. по индексу i от 1 до N,

получим:	T −T		N		(3.2.7)
			= Q Σ R ,
	0	N	i=1	i
или:		Q =	T0 −TN	.	(3.2.8)
			ΣR
			i

Если коэффициенты теплопроводности не зависят от температуры (а с ними и тепловые сопротивления), то по формулам (3.2.5) и (3.2.8) сразу вычисляется значение потока Q. Далее, используя уравнения (3.2.6), можно последовательно, начиная с первого, рассчитать промежуточные температуры Ti на границах слоев:

Ti =Ti−1 −Q(Ti ) Ri (Ti ) (i =1,2......N ). (3.2.9)

Промежуточные температуры необходимо знать, кроме соблюдения математической полноты задачи, и для чисто практических целей. Ведь только исходя из них можно проверить и уточнить выбор теплоизоляционных материалов по их соответствию максимальным температурам эксплуатации.

Выше специально, для упрощения задачи, не учитывалось, что коэффициент теплопроводности зависит от температуры. В реальности, до установления значений температур на границах слоев, мы не можем рассчитать методами классической математики фактические значения величин коэффициентов теплопроводности для всех слоев. Выход из создавшегося положения предоставляет прикладная математика, наука, специализирующаяся на решении задач

численными, прежде всего итерационными методами.

Заметим теперь, что поскольку Ri = f(Ti), то уравнения (3.2.9) являются классической формой рекуррентной записи для их решения методом последовательных приближений (или простых итераций),

когда неизвестная величина является функцией самой себя. Т.е.

форма записи функциональной зависимости имеет вид:
Хi = f(Хi).	(3.2.10)
Алгоритм решения системы (3.2.6) следующий.

Сначала, вне цикла вычисляем постоянные величины – средние площади сечения слоев:

37

Ri(m)

F = Fi−1 − Fi

2

иназначаем начальные значения Ti(0) и потока Q(0), т.е. выбираем по какому-либо правилу нулевое приближение для всех неизвестных величин.

Во всех итерационных методах всегда имеются две фундаментальные проблемы:

1)как выбрать начальное (нулевое) приближение, исходя из которого итерационный процесс всегда сходился бы;

2)что считать решением?

иодна техническая – какая форма записи рекуррентного уравнения более удобна или логична для построения итерационного цикла, и обеспечивает ли она сходимость этого цикла.

В нашем случае сходимость решения абсолютная, и за нулевое

приближение можно принять любые числа. Например, положить все температуры Тi(0) равными (То+ТN)/2, а поток Q(0) равным нулю.

Начало итерационного цикла.

1. Рассчитываем значения коэффициентов теплопроводности:

λi(m) = bi + ki·(Ti-1(m)+Ti(m))/2 ,

где (m) – номер итерации, равный последовательно 1, 2,..., m,...

2. Рассчитываем значения тепловых сопротивлений по (3.2.5):

= Si/(λi(m) · Fi).

3. Рассчитываем приближенное значение Q(m) по (3.2.8):

N

Q(m) = (То – ТN)/ Σ Ri(m). i=1

4. Сравниваем значения Q(m) и прежнего Q, и выполняем логические действия:

а) если Q(m) и Q отличаются не более чем на несколько процентов (например, 2 %), прекращаем вычисления;

б) если расхождение больше – запомним новое численное зна-

чение потока Q(m), выполнив операцию:

Q = Q(m).

5. Рассчитываем уточненные значения температур Тi(m+1) на

внутренних стенках по (3.2.9):

Ti(m+1) = Ti-1(m) – Q·Ri(m).

6. Повторяем итерацию, переходя к этапу 1, т.е. повторяя действия для вычисления нового уточненного значения потока Q(m+1).

38

3.3. Стационарныйтеплообмен. Граничноеусловие3-города

Многослойная стенка с граничным условием третьего рода. Математическая модель и алгоритм решения. Пример компьютерной программы.

Выше была рассмотрена математическая модель с граничным условием первого рода, а именно жесткого задания температуры на внешней стенке (кожухе) печи. Реально этот вариант соответствует мощному теплоотводу, например, сильным потоком воды в кожухе. Однако такое охлаждение достаточно сложно и дорого, и на практике чаще используют воздушное охлаждение, которое значительно менее интенсивно, чем водяное. При воздушном охлаждении температура кожуха достаточно высока и сильно меняется от изменения окружающих условий. В математическом плане наша задача, по сравнению с предыдущей, также усложняется: появляется еще одна неизвестная величина – температура кожуха ТN. Но одновременно возникает дополнительное к системе (3.2.5), (3.2.8) уравнение, отражающее связь температуры кожуха с потоком тепла и температурой окружающей среды.

Из условий связи на границе значения функции (температуры Т в нашем случае) и ее первой производной (потока тепла) наиболее простым является условие линейной связи потоков внутри стенки и

во внешней среде, предложенное И.Ньютоном:
Q = –λ·dT/dx	= α· (T – Tсреды),	(3.3.1)
внутри стенки	во внешней среде

где α – эмпирический коэффициент теплоотдачи. Ньютон считал этот коэффициент постоянным, но на практике коэффициент теплоотдачи чаще всего является функцией температуры. В случае воздухоохлаждаемой печи эта зависимость имеет вид:

α = A·(T – Tсреды)0,25 + ε ·σ· (T 4 – T 4среды)/(T – Tсреды) (3.3.2)

Подставляя (3.3.2) в (3.3.1), получаем формулу для вычисления потока тепла во внешнюю среду со стенки печи:

Qвнешн = A·(Tстенки – Tсреды)1 · (Tстенки – Tсреды)0,25		+
теплопроводность	конвекция
+ ε·σ· (T 4стенки – T 4среды) ,		(3.3.3)
лучистый теплообмен

которое является трансцендентным уравнением относительно температуры, и заведомо не имеющим аналитического решения.

Подписи под формулой (3.3.3) раскрывают физический смысл ее членов: первое слагаемое отражает теплопроводящую и конвек-

39

тивную составляющую теплосъема с кожуха, второе – теплоотдачу излучением. "А" – эмпирический коэффициент, отражающий геометрию системы. Для горизонтальной нижней стенки прямоугольной печи "А" равно 1.63, для верхней стенки – 3.26, для боковой – 2.56. Для цилиндрической печи "А" равно 2.40.

Через ε в (3.3.1) обозначена безразмерная величина – степень черноты кожуха, через σ – постоянная Стефана-Больцмана, равная

5.67·10-8 Вт/м/К4.

Уравнение (3.3.1) устанавливает связь между неизвестной величиной (температурой) и ее первой производной. Этот вариант краевого условия носит название третьей краевой задачи. Решение таких задач значительно сложнее первой краевой.

Нахождение алгоритма численного решения получаемых уравнений является одним из важнейших вопросов в математическом моделировании. Как общую рекомендацию для облегчения поиска алгоритма можно учесть, что очень часто процесс решения третьей краевой задачи сводится к поиску его в классе решений первой краевой. В том числе и при использовании численных методов.

Очень часто выбору алгоритма помогает мысленное исследование физической модели с привлечением математического описания. Например, для выбора алгоритма решения системы уравнений (2.14), (3.2.10), (3.3.1) поставим мысленный эксперимент для определения характера зависимости от температуры TN кожуха печи

двух потоков тепла:
Qвнутр = (То – TN)/ΣRi	внутри твердой стенки и
Qвнешн = α· (TN – Tсреды)	во внешнюю среду

при фиксированных температурах в пространстве печи и окружающей среды.

Из физических соображений очевидно, а из (3.2.8) строго вытекает, что при мысленном увеличении ТN поток из центра печи к наружной стенке Qвнутр уменьшается. Обратная картина наблюдается

для потока Qвнешн с этой стенки во внешнюю среду: согласно (3.3.3), он увеличивается. Следовательно, варьируя ТN, можно подобрать

такое ее значение, при котором расчетные значения потоков в стенке и в среде будут равны, что и соответствует стационарному состоянию (рис. 3.3.1).

40