Михайлов Аналитическая геометрия Учебно-методическое пособие по курсу высшей математики для вечернего фак. 2009

векторов равно нулю. Тогда, используя выражение (4.19), можно произвести следующее преобразование

S

S

S

h

V .

(4.20)

([a b]

c ) = d

c

e

c

Пр c

d

d

(Знак + берем в случае, если тройка векторов правая.)

d

c

Ïð d c

h

e

d

b

a

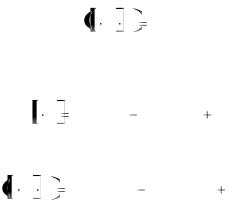
Рис. 4.1

Если же вектора

и

компланарны,

то вектор

лежит в

a, b

c

c

плоскости

векторов

a

и

b ,

следовательно,

h

Прd c

0 и

V S h

0 .

Теорема доказана.

Следствие 1. Справедливо равенство

V

(4.21)

a

b

c

a

b

c

a

b

c

Объѐм параллелепипеда не зависит от того, какая пара векторов из тройки перемножается векторно. Знак произведения не изменяется, так как сохраняется порядок векторов и ориентация тройки векторов.

Следствие 2. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения.

Теорема 4.7. Если три вектора представлены разложениями

по базису i , j , k :
a	i X1	jY1	kZ1, b i X 2			jY2	kZ2 , c i X3			jY3	kZ3 ,

то их смешанное произведение равно следующему определителю:

80

			X1	Y1	Z1
a	b	c	X 2	Y2	Z2	.	(4.22)
			X3	Y3	Z3

Доказательство. Из формулы (4.15) следует, что:

Y Z

X

Z

X

Y

.

a

b

i

1

1

j

1

1

k

1

1

Y2

Z2

X 2

Z2

X 2

Y2

Умножив скалярно этот вектор на вектор c , получим,

			X		Y	Z		Y	X		Z		Z		X		Y	.	(4.23)
a	b	c			1		1			1		1				1	1
				3	Y	Z	2	3	X	2	Z	2		3	X	2	Y
					2												2

Полученное выражение (4.23) есть разложение определителя (4.22) по элементам третьей строки.

Теорема доказана.

Задачи для самостоятельного решения [2]: № 795, 800, 803, 812, 818,

820, 829, 834, 840, 847, 851, 858, 875, 877.

Вопросы для повторения

1.Скалярное произведение, определение. Геометрические и алгебраические свойства.

2.Скалярное произведение в декартовых координатах, (доказать).

3.Угол между векторами, условия перпендикулярности векторов.

4.Проекция одного вектора на другой или на произвольную ось.

5.Определение векторного произведения. Тройка векторов. Геометрические и алгебраические свойства векторного произведения.

6.Векторное произведение в декартовых координатах (доказать).

7.Условия коллинеарности векторов (доказать)

8.Смешанное произведение трех векторов. Геометрическая интерпретация (доказать). Условие компланарности трех векторов.

9.Смешанное произведение трех векторов в декартовых координатах (доказать).

81

			X1	Y1	Z1
a	b	c	X 2	Y2	Z2	.	(4.22)
			X3	Y3	Z3

Доказательство. Из формулы (4.15) следует, что:

Y Z

X

Z

X

Y

.

a

b

i

1

1

j

1

1

k

1

1

Y2

Z2

X 2

Z2

X 2

Y2

Умножив скалярно этот вектор на вектор c , получим,

			X		Y	Z		Y	X		Z		Z		X		Y	.	(4.23)
a	b	c			1		1			1		1				1	1
				3	Y	Z	2	3	X	2	Z	2		3	X	2	Y
					2												2

Полученное выражение (4.23) есть разложение определителя (4.22) по элементам третьей строки.

Теорема доказана.

Задачи для самостоятельного решения [2]: № 795, 800, 803, 812, 818,

820, 829, 834, 840, 847, 851, 858, 875, 877.

Вопросы для повторения

10.Скалярное произведение, определение. Геометрические и алгебраические свойства.

11.Скалярное произведение в декартовых координатах, (доказать). 12.Угол между векторами, условия перпендикулярности векторов. 13.Проекция одного вектора на другой или на произвольную ось.

14.Определение векторного произведения. Тройка векторов. Геометрические и алгебраические свойства векторного произведения.

15.Векторное произведение в декартовых координатах (доказать). 16.Условия коллинеарности векторов (доказать)

17.Смешанное произведение трех векторов. Геометрическая интерпретация (доказать). Условие компланарности трех векторов.

18.Смешанное произведение 3-х векторов в декартовых координатах (доказать).

82

5.ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ

5.1.Общее уравнение прямой

Определение 5.1. Уравнение

F x, y 0

(5.1)

называется уравнением линии на плоскости относительно заданной системы координат, если ему удовлетворяют координаты точек, принадлежащих некоторой линии L, и не удовлетворяют координаты точек, не принадлежащих этой линии.

Определение 5.2. Линия называется алгебраической, если в некоторой прямоугольной системе координат F(x,y) есть полином некоторой степени.

Алгебраическая линия называется линией n-го порядка если F(x,y) − полином степени n.

Теорема 5.1. Если линия в некоторой прямоугольной системе координат определяется алгебраическим уравнением степени п, то и в другой прямоугольной системе координат степень уравнения будет равна п.

Без доказательства.

В трехмерном пространстве определения 5.1 и 5.2 и утверждение теоремы 5.1 можно повторить, заменив слово «линия» словом «поверхность».

Теорема 5.2. Если на плоскости фиксирована прямоугольная система координат Оху, то любая прямая L, принадлежащая плоскости, определяется в этой системе координат уравнением первой степени.

Доказательство. При специальном выборе системы координат, если ось Ох совпадает с прямой, уравнение прямой у = 0 совпадает с уравнением оси Ох. В соответствии с утверждением теоремы 5.1 в любой другой прямоугольной системе координат степень уравнения сохранится.

Пусть уравнение прямой имеет вид:

A x B y C 0 ,	A		B	0 .	(5.1)
83

Пусть задана точка М0(х0, у0), координаты которой удовлетво-

ряют уравнению

A x0

B y0

C

0 .

(5.2)

Вычитая (5.2) из (5.1), получаем

A

x

x0

B

y

y0

0 .

(5.3)

Дадим векторное истолкование уравнения (5.3).

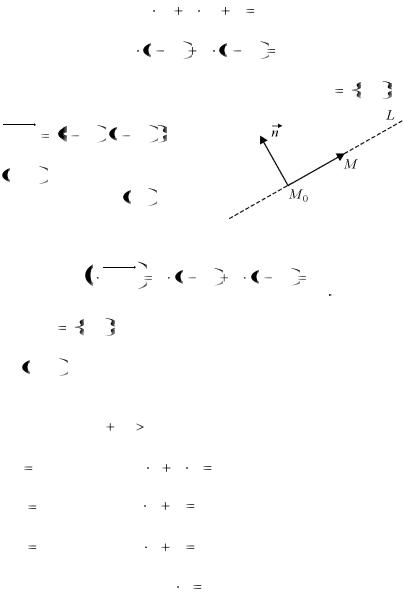
Пусть

А и

В − координаты

некоторого

вектора

A, B , а

n

(х – х0) и (у – у0) − компоненты векто-

ра M0M

x

x0 ,

y

y0

, начало

которого

совпадает

с

точкой

M0 x0 , y0

, а конец совпадает с про-

извольной

точкой

M x, y ,

принад-

лежащей прямой (рис. 5.1).

Рис. 5.1

Очевидно, что скалярное произве-

дение

n M0M A x x0

B y y0 0

является условием ортогональности векторов

n и M 0M .

A, B называется нормальным вектором прямой.

Вектор n

Уравнение (5.3) есть уравнение прямой, проходящей через точ-

ку M0 x0 , y0 перпендикулярно вектору n . Уравнение (5.3) экви-

валентно уравнению (5.1), которое называется общим уравнением

прямой.

При условии		A		B	0 рассмотрим неполные уравнения пря-
мой.
1) C	0 . Уравнение				A x	B	y 0 определяет прямую, прохо-
дящую через начало координат.
2) A	0 . Уравнение B y					C	0 определяет уравнение прямой,
параллельной оси Ox .
3) B	0 . Уравнение A x					C	0 определяет уравнение прямой,
параллельной оси Oy .
4) А = 0, С = 0. Уравнение B y							0 определяет уравнение оси Ох.
						84

5) В = 0, С = 0. Уравнение Ax 0 определяет уравнение оси Оу. Из уравнения (5.1) можно получить уравнение прямой в отрез-

ках:
		x				y		1 .	(5.4)
		a				b
В самом деле, уравнение
	x					y		1	(5.5)
	C					C

A B

получено из уравнения (5.1) с помощью элементарных алгебраиче-

ских преобразований. Обозначив a 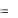CA , b 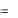CB , получим урав-

нение (5.4).

Чтобы найти координаты точки пересечения прямой с осью Ox , решим систему уравнений, состоящую из уравнения (5.4) и уравнения оси Ox .

	x		y	1,	x
						1 x a .	(5.6)
	a		b
					a
		y		0

Аналогично можно получить, что y b координата точки пересечения с осью Oy .

Определение 5.3. Любой ненулевой вектор, параллельный данной прямой, будем называть направляющим вектором прямой.

Пример 5.1. Составить уравнение прямой L, проходящей через

точку M1 x1, y1 параллельно вектору q l, m .

Решение. Рассмотрим вектор

M1M 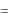x x1 , y y1, начало которого совпадает с точкой M1 , а конец − в произвольной точке M x, y

(рис. 5.2).

Чтобы точка M лежала на прямой

Рис. 5.2

L , вектор M1M должен быть парал-

85

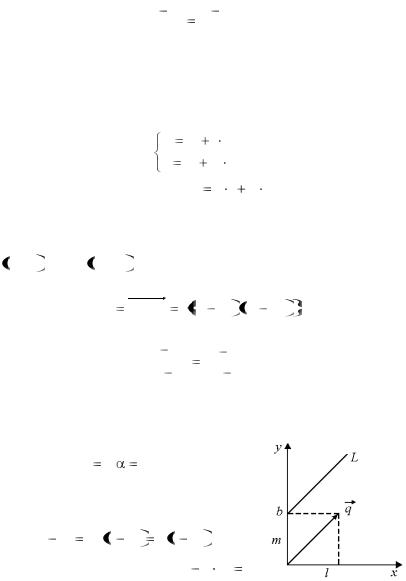
лелен вектору q . Условие параллельности векторов состоит в пропорциональности сходственных координат, из чего следует

x x1		y y1	.	(5.7)
l		m

(Нуль в знаменателе в этой пропорции означает, что соответствующий числитель тоже обращается в нуль.)

Это уравнение называется каноническим уравнением прямой.

Приравняв выражение (5.7) параметру t , получим параметри-

ческие уравнения прямой:

	x		x1	l	t,	(5.8)
	y	y1		m t.
	Если принять что, t − время, а					вектор скорости, то
			v	i	l j m

уравнения (5.8) определяют две проекции уравнения движения точки на координатные оси.

Уравнение прямой,	проходящей						через		две заданные точки
M1 x1, y1 и M2 x2 , y2 ,	получим из уравнения (5.7),									приняв, что
направляющий вектор
q M1M 2				x2			x1 y2		y1 ,	(5.9)
и подставив выражение (5.9) в (5.7):
		x	x			y	y1	.		(5.10)
		x2	x1 y2				y1
Уравнение прямой с угловым коэффициентом										k получим,

приняв, что угловой коэффициент равен тангенсу угла наклона на-

правляющего вектора q (рис. 5.3):
	k			tg		m	.		(5.11)
						l
Умножив выражение (5.7) на число m и
подставив в него (5.11), получим:
y y		m		x	x k x			x .	(5.12)
1			l		1			1
Если принять обозначение y1								k	x1 b ,
уравнение примет вид									Рис. 5.2
					86

y k x b .

(5.13)

Здесь y b координата точки пересечения прямой L с осью Oy, в чем легко убедиться, подставив в (5.13) уравнение оси Oy − x = 0.

Косинус угла между прямыми, а также условия перпендику-

лярности и параллельности прямых очевидным образом связаны с соответствующими соотношениями между векторами: нормаль-

, и направляющим −

ным − n

q .

cos

n1

n2

A1

A2

B1

B2

,

(5.14)

n1

n2

A12

B12

A22 B22

cos

q1 q2

l1

l2

m1 m2

.

(5.15)

q1

q2

l12

m12

l22

m22

Условия перпендикулярности двух прямых:

A1

A2

B1

B2 l1 l2

m1

m2 0 .

(5.16)

Условия параллельности прямых:

A1

B1

, или

l1

m1

(5.17)

A2

B2

l2

m2

(ноль в знаменателях этих пропорций означает, что соответствующие числители тоже обращаются в ноль).

В случае двух прямых с угловым коэффициентом

						2		1,
tg	tg	2	1			tg 2			tg	1		k2	k1	.	(5.18)
				1		tg		1 tg			1		k1k2
										2
Условие параллельности
				k2		k1 ,									(5.19)
условие перпендикулярности
				k2				1	.						(5.20)
							k1

Чтобы получить нормальное уравнение прямой из начала ко-

ординат опустим перпендикуляр на прямую L (рис. 5.4). Пусть Р − точка пересечения перпендикуляра с прямой L, длина отрезка

OP	p , орт нормали en	cos ,sin . Чтобы точка M x, y ле-
		87

жала на прямой, необходимо и достаточно, чтобы проекция вектора

OM 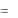x, y на нормаль равнялась р:

			y sin p .
Прn OM en	OM	x cos
Уравнение
x cos		y sin	p 0

есть нормальное уравнение прямой.

Пусть d − расстояние от точки M0 x0 , y0 до прямой. Отклонение

точки от прямой 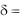d , если точка и начало координат лежат по разные стороны от прямой, и 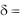d , если точка и начало координат лежат по одну сторону от прямой.

PQ	OQ	p			(5.23)
x0 cos	y0	sin		p.		Рис. 5.2
Здесь
OQ Прn OM0			en	OM0 x0		cos y0 sin .

(5.21)

(5.22)

(5.24)

Очевидно, что общее уравнение	прямой Ax	By	C 0 и
нормальное уравнение прямой x cos	y sin	p 0	определя-

ют одну и ту же прямую. Следовательно, существует такое число , что

A cos	,	B	sin	,	C p , p			0 .			(5.25)
cos2 sin2	1	2	A2	B2	1					.	(5.26)
							A2	B2
Из третьего равенства выражения (5.25) следует, что знак											про-
тивоположен знаку С.		Число	называется нормирующим мно-

жителем.

Для получения нормального уравнения прямой достаточно умножить общее уравнение на нормирующий множитель .

Определение 5.3. Множество прямых, принадлежащих плоскости , пересекающихся в точке S0, называется пучком прямых.

88

Теорема 5.3. Уравнение
A1x B1y C1	A2x B2 y C2	0	(5.27)
есть уравнение пучка прямых, пересекающихся в точке S, если и
не обращаются в нуль одновременно, а уравнения
A1x B1y C 0 и	A2x B2 y C	0	(5.28)

суть уравнения двух прямых, пересекающихся в точке S0. Любая прямая, проходящая через точку S0, определяется уравнением

(5.27) при некоторых значениях чисел				и .
Доказательство. Преобразуем уравнение к следующему виду:
A1	A2 x	B1	B2 y	C1	C2 0 .	(5.29)

Это уравнение прямой, если выражения в скобках не равны нулю одновременно. Предположим противное: пусть обе первые скобки равны нулю. Тогда

из	A1	A2	0	следует	A1			,
					A2
из	B1	B2	0	следует	B1			.
					B2

В итоге

A1		B1	.	(5.30)
A2		B2

Это условие параллельности прямых (5.28) противоречит условиям теоремы. Тем самым доказано, что уравнение (5.27) всегда определяет некоторую прямую.

Эта прямая проходит через точку S0 x0 , y0 , так как подстанов-

ка еѐ координат обращает в нуль каждое из уравнений (5.28), а следовательно, и уравнение (5.27).

A1x0 B1y0	C1	A2x0 B2 y0	C2	0 .	(5.31)
Покажем, что любая прямая, принадлежащая пучку определя-
ется уравнением (5.27) при некоторых значениях чисел				и	. Фик-
сируем точку M1 x1, y1 ,	отличную от точки		S0 x0 , y0 .		Эти две

точки определяют прямую, принадлежащую пучку, единственным образом.

89