Михайлов Аналитическая геометрия Учебно-методическое пособие по курсу высшей математики для вечернего фак. 2009

Подставив координаты точки				M1 в уравнение (5.27), получим
уравнение относительно неизвестных					и	:
A1x1	B1y1		C1	A2x1			B2 y1	C2 0 .	(5.32)
В этом уравнении круглые скобки не могут обратиться в нуль
одновременно, так как точка M1				не может принадлежать двум раз-
личным прямым, так как не совпадает с точкой S0								(5.28).
Пусть
	A1x1		B1y1 C1		0 ,
Тогда
		A2 x1		B2 y1	C2		.		(5.33)
			A1x1	B1y1	C1
Из (5.33) значения	и		определяются с точностью до произ-

вольного общего множителя.

Можно представить уравнение пучка прямых в другом виде,

разделив (5.27) на		0 и положив				:
	A1x B1y C1			A2x B2 y		C2 0 .	(5.34)
Уравнение (5.34) не эквивалентно (5.27), так как не позволяет
получить прямую A2x		B2 y	C2	0 .
Случай	0 предоставляется рассмотреть читателю.
	5.4. Примеры решения типовых задач
Пример 5.1. Дана прямая			A1x	B1y C1		0 и точка M0	x0 , y0 .

Составить уравнение прямой, походящей через данную точку параллельно заданной прямой.

Решение. Нормальный вектор прямой n1			A1, B1 , он же будет
нормальным вектором искомой прямой.
Чтобы «свободная точка»		M x, y принадлежала искомой пря-
мой, вектор M0M	x x0 ,	y y0 должен быть перпендикуля-

рен вектору n1 . Условие перпендикулярности векторов

90

n1	M0M A1	x x0	B1	y y0 0
есть искомое уравнение. Раскрыв скобки				и введя обозначение
C2 A1x0 B1y0	запишем найденное уравнение в общем виде
	A1x B1y C2		0 .
Пример 5.2. Дана прямая		A1x B1y	C1	0 и точка M0 x0 , y0 .

Составить уравнение прямой, походящей через данную точку перпендикулярно заданной прямой.

Решение. Нормальный вектор прямой n1								A1, B1 будет направ-
ляющим вектором для искомой прямой.
Чтобы «свободная точка»			M x, y			принадлежала искомой пря-
мой, вектор M0M	x x0 ,		y	y0		должен быть параллелен век-
тору n1 . Условие параллельности векторов
		x	x0		y	y0		(5.35)
		A1			B1

есть искомое уравнение в каноническом виде. Умножив (5.35) на

произведение A1 B1 0 и введя обозначение C3	B1x0 A1y0 за-
пишем искомое уравнение в общем виде
B1x A1y C3 0 .	(5.36)

Условия A1 0 или B1 0 означают, что соответствующие чис-

лители обращаются в нуль.

Заметим, что в случае перпендикулярности прямых коэффициенты при переменных x и y меняются местами, а у одного из них

меняется знак.
Пример 5.3. Заданы уравнение пучка прямых
A1x B1y C1	A2x	B2 y C2 0 ,	(5.37)
и прямая L3
A3x	B3 y C3	0 .

Составить уравнение прямой, принадлежащей пучку, парал-

лельной прямой L3 .
Решение. Преобразуем уравнение (5.37)
A1	A2 x B1	B2 y C1	C2 0 ,
		91

Нормальный вектор n		A1		A2 , B1		B2		параллелен векто-
ру n3	A3, B3 . Условие параллельности векторов
		A1	A2 B1			B2
		A3			B3
содержит единственную неизвестную величину								. Определив и

подставив его в уравнение (5.37), получим искомое уравнение.

Задачи для самостоятельного решения [2]: № 213, 223, 234, 236, 248,

261, 271, 292, 310, 312, 313, 315, 323, 334, 337, 349, 354.

Вопросы для повторения

1.Общее уравнение прямой линии на плоскости. Векторное истолкование уравнения прямой. Нормальный вектор прямой. Уравнения прямых частного положения. Уравнение прямой «в отрезках». Геометрическая интерпретация. Основные задачи, решаемые с помощью уравнений этих типов.

2.Направляющий вектор прямой. Каноническое и параметрические уравнения прямой. Уравнение прямой с угловым коэффициентом. Основные задачи, решаемые с помощью уравнений этих типов.

3.Угол между прямыми. Условия параллельности и перпендикулярности прямых.

4.Нормальное уравнение прямой. Нормирующий множитель. Отклонение точки от прямой. Основные задачи для нормального уравнения прямой.

5.Определение пучка прямых. Уравнение пучка прямых. Основные задачи для уравнения пучка.

6.ПЛОСКОСТЬ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ

6.1. Общее уравнение плоскости

Теорема 6.1. Если в пространстве выбрана некоторая прямоугольная система координат, то уравнение первой степени относительно переменных x, y, z

A x B y C z D 0	(6.1)
92

определяет в этой системе координат некоторую плоскость (при условии, что коэффициенты А, В, С не обращаются в нуль одновременно).

Найдется точка M0 x0. y0 , z0 , координаты которой удовлетворяют уравнению (6.1):

A x0	B y0	C z0	D	0 .	(6.2)
Вычитая уравнение (6.2) из (6.1), получим уравнение,					эквива-
лентное исходному уравнению.
A x x0	B y	y0	C z	z0 0 .	(6.3)

Это уравнение есть условие ортогональности нормального век-

тора n A, B, C и вектора

M0M x x0 , y y0 , z z0 ,

начало которого в фиксированной точке M0 x0 , y0 , z0 , а конец в свободной точке М с произвольными координатами x, y и z (рис.

6.1).

		Рис. 6.1
	Вектор M 0M может изменять длину и вращаться вокруг векто-
ра		, оставаясь перпендикулярным к нему. Свободная точка
	n

M x, y, z , являющаяся концом вектора, будет при этом переме-

щаться по плоскости,	проходящей через точку M0 x0 , y0 , z0 пер-
пендикулярно вектору
	n .
Следовательно, уравнение (6.3) есть уравнение плоскости с
нормальным вектором
	n , проходящей через фиксированную точку

M0 . Теорема доказана.

Уравнение (6.1), эквивалентное уравнению (6.3), называется общим уравнением плоскости.

93

Рассмотрим неполные уравнения

плоскости при

условии

A

B

C

0 :

1)

D

0 .

Уравнение

A x

B

y

C

z

0 определяет плос-

кость, проходящую через начало координат.

2)

A

0 . Уравнение

B y

C z

D

0 определяет плоскость,

0, B, C

параллельную оси Ox, так как еѐ нормальный вектор n

перпендикулярен оси Ox.

3)

A

0, B

0 .

Уравнение

C z

D

0 определяет плоскость,

перпендикулярную

оси

Oz ,

так

как

еѐ

нормальный

вектор

n 0, 0, C параллелен оси Oz .

Остальные неполные уравнения плоскости рассматриваются аналогично.

Уравнение плоскости «в отрезках» легко получить из уравнения (6.1), если перенести свободный член D направо от знака равенства, разделить на него левую часть уравнения и сделать очевидные

алгебраические преобразования:

x

y

z

1.

(6.4)

D

D

D

A

B

C

Введем обозначения

D

a,

D

b,

D

c ,

уравнение (6.4)

A

B

C

примет вид

x

y

z

1 .

(6.5)

a

b

c

Здесь числа a, b и c равны коорди-

натам точек пересечения плоскости с

осями координат (рис. 6.2).

Уравнение (6.5) имеет смысл при

B

C

0 .

условиях D 0 и

A

Убедиться в этом можно, решив

систему уравнений, состоящую из

уравнения плоскости (6.5) и уравнений

осей координат, например оси Ox:

Рис. 6.2

94

x		y		x	1
a		b		c		x
		y	0				1 x a .	(6.6)
						a
		z	0

Доказательства для точек b и с проводятся аналогично.

Угол между плоскостями и условия параллельности и пер-

пендикулярности плоскостей очевидным образом связаны с соответствующими условиями для их нормальных векторов

Пусть заданы уравнения двух плоскостей

	1 : A1x B1 y C1z D1	0,	(6.7)
	2 : A2 x B2 y C2 z D2	0.

Угол между плоскостями равен углу между нормальными векторами этих плоскостей. В данном случае это вектора

n1	A1, B1, C1 и n2	A2 , B2 , C2 .

Косинус угла между векторами можно найти исходя из определения скалярного произведения

n1	n2	n1		n2	cos

cos

n1

n2

A1 A2

B1

B2

C1

C2

.

(6.8)

n1

n2

A12 B12

C12

A22

B22 C22

Условие ортогональности плоскостей следует из условия ортогональности их нормальных векторов, то есть равенства нулю их скалярного произведения:

n1	n2	0	A1 A2 B1 B2 C1 C2 0 .	(6.9)

Условия параллельности плоскостей следуют из условия колли-

неарности их нормальных векторов:
	A1		B1		C1	.	(6.10)
	A2		B2		C2

Пример 6.1. Составить уравнение плоскости, проходящей через три заданные точки.

Решение. Пусть заданы точки M1 x1, y1, z1 , M2 x2 , y2 , z2 , M3 x3, y3, z3 , не принадлежащие одной прямой. Тогда вектора

95

и M1M 3

M1M 2 x2 x1; y2 y1; z2 z1 ,	M1M3 x3		x1; y3 y1; z3 z1
не будут коллинеарными. Пусть точка		M x, y, z	«свободная точ-
ка» с произвольными координатами x,		y, z , а вектор

M1M x x1; y y1; z z1

– «свободный» вектор. Чтобы точка М (х, у, z) принадлежала плоскости, определяемой векторами M1M 2 необходимо и

достаточно, чтобы все три вектора были компланарны, а их смешанное произведение равнялось нулю:

					x	x1	y	y1	z	z1
M1M	M1M 2 M1M3				x2	x1	y2	y1	z2	z1	0 . (6.11)
					x3	x1	y3	y1	z3	z1
Уравнение (6.11) есть уравнение искомой плоскости.
	6.2. Нормальное уравнение плоскости.
	Отклонение точки от плоскости
Рассмотрим плоскость				(рис 6.3). Из
начала координат проведем нормаль к
этой плоскости. Точку пересечения нор-
мали с плоскостью обозначим Р. Вели-
чину отрезка ОР обозначим р. Орт нор-
мали OP обозначим en :
en	cos	; cos	; cos .
Чтобы свободная			точка M x,				y, z
принадлежала плоскости ,				необходимо						Рис. 6.3
и достаточно чтобы проекция радиуса-
вектора OM	x	0, y	0, z	0		x, y, z		точки М на нормаль OP
равнялась числу р.

Прn OM OM en x cos y cos z cos p . (6.12)

Нормальное уравнение плоскости получим, если в (6.12) перенесем влево от знака равенства число р:

96

x cos

y cos

z cos

p 0

(6.13)

Отклонение точки от плоскости. Пусть число d PQ −

расстояние от точки M0 x0 , y0 , z0 до плоскости. Отклонение точки от плоскости 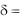d , если точка и начало координат лежат по разные стороны от плоскости, и d , если точка и начало координат лежат по одну сторону от плоскости:

PQ OQ	p	x0	cos	y0	cos	z0 cos p .		(6.14)
Здесь
							z0 cos .	(6.15)
OQ Прn OM0	en OM0		x0 cos		y0 cos
Нормальное уравнение плоскости (6.13)
x cos		y cos		z cos		p	0
и общее уравнение плоскости (6.1)
	A x	B y		C z	D	0

определяют одну и ту же плоскость, следовательно, существует

такое число , что

A cos ,

B

cos ,

C

cos ,

D

p ,

(6.16)

cos2

cos2

cos2

1

2

A2

B2

C 2

1

.

(6.17)

A2

B2

C 2

Из четвертого равенства выражения (6.16) следует, что знак

противоположен

знаку

D.

Число

называется

нормирующим

множителем. Для получения нормального уравнения плоскости достаточно умножить общее уравнение на нормирующий множитель .

Отклонение точки от плоскости получим, подставив координаты точки M0 x0 , y0 в уравнение (6.14).

6.3. Уравнение пучка плоскостей

Определение 6.1. Множество плоскостей, пересекающихся по одной прямой L, называется пучком плоскостей.

97

Теорема 6.2. Уравнение
A1x B1y C1z D1			A2x	B2 y C2z		D2	0	(6.18)
есть уравнение пучка плоскостей, если				и не обращаются в нуль
одновременно, а уравнения
A1x B1y C1z D1		0 и A2x		B2 y C2z		D2	0	(6.19)
суть уравнения двух плоскостей, пересекающихся по прямой L.
Любая плоскость, проходящая через прямую L, определяется
уравнением (6.19) при некоторых значениях чисел						и .
Доказательство. Преобразуем уравнение к виду
A1	A2	x	B1	B2	y			(6.20)
C1	C2	z	D1	D2	0.

Это – уравнение плоскости, если выражения в скобках не равны нулю одновременно. Предположим противное. Тогда

из

A1

A2

0

следует

A1

,

A2

из

B1

B2

0

следует

B1

,

B2

из

D1

D2

0

следует

D1

.

D2

В итоге

A1

B1

D1

.

(6.21)

A2

B2

D2

Это – условие параллельности плоскостей (6.19), что противоречит условиям теоремы. Тем самым доказано, что уравнение (6.18) всегда определяет некоторую плоскость.

Покажем, что любая плоскость, принадлежащая пучку определяется уравнением (6.18) при некоторых значениях чисел и . Фиксируем точку M1 x1, y1, z1 , не принадлежащую прямой L. Точ-

ка M1 и прямая L определяют плоскость, принадлежащую пучку,

единственным образом.
Подставив координаты точки M1	в уравнение (6.18), получим
уравнение относительно неизвестных	и :
98

A1x1	B1y1 C1z1			D1		A2x1	B2 y1		C2z1 D2	0 .
В этом уравнении выражения в круглых скобках не могут обра-
титься в нуль одновременно,					так как точка M1				не может принад-
лежать двум различным плоскостям (6.19).
Пусть A1x1	B1y1	C1z1		D1 0 , тогда
			A2 x1		B2 y1	C2 z1	D2		.	(6.22)
			A1x1		B1y1	C1z1	D
Из (6.22) значения			и		определяются с точностью до произ-

вольного общего множителя.

Можно представить уравнение пучка плоскостей в другом виде,

разделив (6.18) на и положив			:	0 .	(6.23)
A1x B1y C1z D1	A2x B2 y C2z D2
6.4. Примеры решения типовых задач
Пример 6.2. Дана плоскость	A1x B1y C1z D1 0			и	точка

M0 x0 , y0 , z0 . Составить уравнение плоскости, походящей через

данную точку параллельно заданной плоскости.

Решение.

Нормальный

вектор

заданной

плоскости

n1

A1, B1,C1

, он же будет нормальным вектором искомой плос-

кости.

Чтобы «свободная точка»

M x, y, z принадлежала искомой

плоскости,

вектор

M0M

x

x0 ,

y

y0 ,

z z0

должен

быть

перпендикулярен вектору

n1 . Условие перпендикулярности векто-

ров

n1

M0M

A1

x

x0

B1

y

y0

C1 z z1

0

(6.24)

есть

искомое

уравнение.

Раскрыв скобки и введя обозначение

D2

A1x0

B1y0 C1z0

запишем найденное уравнение в общем

виде A1x

B1y

C2 z

D2

0 .

99