Е.Н. Грибанов Теория вероятностей и математическая статистика. Методические указания для студентов специальности 230500 - Социальный сервис и туризм

-50-

большая или равная половине всех наблюдений (≥ 0,5); meнак (ωенак )-

частота (частость), накопленная к началу медианного интервала; me (ωe )- частота (частость) медианного интервала.

(~ )

О.2. Модой Mo называют такое значение признака, которое

наблюдалось наибольшее число раз. Нахождение моды для дискретного вариационного ряда не требует каких-либо вычислений, так как ей является вариант, которому соответствует наибольшая частота.

В случае интервального вариационного ряда мода вычисляется по следующей формуле:

	M0 = a0 + h	m0 − m0′	или M0 = a0 + h	ω0 −ω0′	,
		2m0 − m0′ − m0′′		2ω0 −ω0′ −ω0′′

где a0 - начало модального интервала, то есть такого, которому соответствует наибольшая частота (частость); m0 (ω0 ) - частота (частость) модального интервала; m0′ (ω0′ ) - частота (частость) интервала, предшествующего модальному; m0′′ (ω0′′) - частота (частость) интер-

вала, следующего за модальным.

Моду используют в случаях, когда нужно ответить на вопрос, какой товар имеет наибольший спрос, каковы преобладающие в данный момент уровни производительности труда, себестоимости. Модальные производительность и себестоимость помогают вскрыть ресурсы, имеющиеся в экономике.

Пример 37. Вычислить моду и медиану для интервального ряда

Интервалы

3 - 7

7 - 11

11 - 15

15 - 19

19 - 23

23 – 27

Частоты

6

9

11

12

8

4

,

или

Решение. Найдём объём выборки по формуле

n = ∑mi

n = 6 +9 +11+12 +8 +4 = 50. Вычислим накопленные частоты

тнак = 6; т

нак = 6 +9 =15; тнак = 6 +9 +11 = 26 , следовательно,

ме-

1

2

3

дианным является интервал [11−15]. Тогда ае =11, тенак =15 ,

те =11

~

25 −15

≈14,36.

и Ме =11+ 4

11

[15 −19],

a0 =15,

Модальным

является

интервал

следовательно,

~

12 −11

m0 =12, m0′ =11, m0′′ =8 . Тогда M0 =15 + 4

=15,8 .

24 −11−8

-51-

34. Показатели вариации Средние величины, характеризуя вариационный ряд числом, не

отражают изменчивости наблюдавшихся значений признака, то есть вариацию. Простейшим показателем вариации является вариационный размах R0 , равный разности между наибольшим и наименьшим

вариантами: R0 = xmax − xmin .

Вариационный размах – приближённый показатель вариации, так как почти не зависит от изменения вариантов, а крайние варианты которые используются для его вычисления, как правило, ненадёжны.

Более содержательными являются меры рассеяния наблюдений вокруг средних величин. Средняя арифметическая является основным видом средних, поэтому ограничимся рассмотрением мер рассеяния наблюдений вокруг средней арифметической.

Средним линейным отклонением (d ) называют среднюю ариф-

метическую абсолютных величин отклонений результатов наблюде-

ний от их средней арифметической d =	1	n		xi − x
		∑				.
	n i =1

Эмпирической дисперсией (S 2 )называют среднюю арифметическую квадратов отклонений результатов наблюдений от их средней

				1	n
	арифметической	S 2	=		∑(xi − x)2 .	Если по результатам наблюде-
				n i =1
	ний построен	вариационный ряд,				то эмпирическая дисперсия

S2 = n1 ∑(xi − x)2 mi .

Вместо эмпирической дисперсии в качестве меры рассеяния наблюдений вокруг средней арифметической часто используют эмпирическое среднее квадратическое отклонение, равное арифметическому значению корня квадратного из дисперсии и имеющее ту же размерность, что и значения признака. Для вариационного ряда среднее квадратическое отклонение:

S = 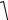n1 ∑(xi − x)2 mi .

-52-

Свойства эмпирической дисперсии

1.Дисперсия постоянной величины равна нулю.

2.Если все результаты наблюдений уменьшить (увеличить) на одно и то же число, то дисперсия не изменится.

3.Если все результаты наблюдений уменьшить (увеличить) в одно и то же число k раз, то дисперсия уменьшится (увеличится) в k2 раз.

4.Эмпирическая дисперсия равна разности между средней арифметической квадратов наблюдений и квадратом средней ариф-

метической S 2 = x2 −(x)2 .

Пример 38. Найти эмпирическую дисперсию и выборочное среднее квадратическое отклонение для следующего интервального вариационного ряда

Интервалы

3 – 7

7 - 11

11 - 15

15 - 19

19 - 23

23 – 27

Частоты

6

9

11

12

8

4

Решение.

Эмпирическую

дисперсию

найдём

по формуле

S2 =

−(x)2 и

= n1 ∑ xi2mi где xi - середины интервалов

x2

x2

mi

- соответствующая частота, тогда

=

1

(52 6 +92 9 +132 11+172 12 + 212 8 + 252 4)=

12234

x2

=

50

50

= 244,6,

x =14,52,

S 2 = 244,68 −14,522 = 33,8496.

35. Эмпирические центральные и начальные моменты Средняя арифметическая и дисперсия вариационного ряда яв-

ляются частными случаями более общего понятия о моментах вариационного ряда.

О.1. Эмпирическим начальным моментом (νk ) порядка k назы-

вают взвешенную среднюю арифметическую k-х степеней вариантов

ν~k = xk = n1 ∑ xik mi .

~ )

О.2. Эмпирическим центральным моментом (µk порядка k на-

зывают взвешенную среднюю арифметическую k-х степеней откло-

нений		вариантов				от	их	средней	арифметической
~				1		k
		k					mi .
µk = (x − x) =				n	∑(xi − x)

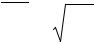
-53-

Эмпирический

1

центральный

момент

нулевого

порядка

равен

~

0

0

=

µ0

= (x − x)

n

∑(xi − x) mi =1.

Эмпирический

центральный

момент

первого

порядка

равен

1

~

1

1

µ1

= (x − x) =

n

∑(xi − x) mi = 0 .

Эмпирический

центральный

момент

второго

порядка

равен

1

~

2

~

~2

2

2

=

=

S

.

µ2

= (x − x)

n

∑(xi − x) mi =ν2

−ν1

Эмпирический

центральный

момент

третьего

порядка

равен

1

~

3

~

~ ~

~3

3

µ3

= (x − x)

= n

∑(xi − x) mi

=ν3

−3ν2ν1

+

2ν1 .

Эмпирический

1

центральный

момент

четвёртого

порядка

равен

~

4

~

~ ~

~ ~2

~4

4

=

µ4

= (x − x)

n

∑(xi − x) mi =ν4

−4ν

3ν1 +6ν2ν1

−3ν1 .

Рассмотрим свойства центральных моментов, которые позволяют значительно упростить их вычисление.

1. Если все варианты уменьшить (увеличить) на одно и то же число, то центральный момент k-го порядка не изменится.

2. Если все варианты уменьшить (увеличить) в одно и то же число q раз, то центральный момент k-го порядка уменьшится (увеличится) в qk раз.

36. Эмпирические асимметрия и эксцесс

(~)

Эмпирическим коэффициентом асимметрии A называют от-

ношение центрального момента третьего порядка к кубу среднего
	~	~			~
		µ	3		µ	3
квадратического отклонения	A =			=			.
					~3
		S	3
					µ2

Если полигон вариационного ряда скошен, то есть одна из его ветвей, начиная от вершины, зримо длиннее другой, то такой ряд называют асимметричным. Если в вариационном ряду преобладают варианты, меньшие x , то эмпирический коэффициент асимметрии отрицателен, и в этом случае имеет место левосторонняя асимметрия. Если же в вариационном ряду преобладают варианты, большие x , то эмпирический коэффициент асимметрии положителен, и в этом случае имеет место правосторонняя асимметрия. При левосторонней

-54-

асимметрии левая ветвь длиннее правой. При правосторонней, более длинной является правая ветвь.

Эмпирический коэффициент асимметрии не имеет ни верхней, ни нижней границы, что снижает его ценность как меры асимметрии. Практически коэффициент асимметрии редко бывает особенно велик,

а для умеренно асимметричных рядов он обычно меньше единицы.

(~)

Эмпирическим эксцессом или коэффициентом крутости E

называют уменьшенное на три единицы отношение центрального

момента четвёртого порядка		к		четвёртой степени среднего
~		~			~
		µ	4		µ	4
квадратического отклонения: E	=			−3 =			−3.
		S	4		~2
					µ	2

За стандартное значение эксцесса принимают нуль-эксцесс нормальной кривой распределения. Кривые, у которых эксцесс отрицательный, по сравнению с нормальной менее крутые, имеют более плоскую вершину и называются «плосковершинными». Кривые с положительным эксцессом более крутые по сравнению с нормальной кривой, имеют более острую вершину и называются «островершинными».

Т. Коэффициенты асимметрии и эксцесса не зависят от выбора

начало отсчёта и единицы измерения, то есть для любых постоянных
a ≠ 0 и b,	~	~	~	~	(x).
	A(ax +b)= A(x), E			(ax +b)= E

Доказательство. По свойствам эмпирических центральных моментов

~

~

(ax +b)

a

3

~

(x)

~

имеем

µ

3

=

µ

=

и

A(ax +b)=

3

µ

2

(x)

A(x)

(µ(ax +b))

a

~

3

~3

~

~

(ax +b)

a

4

~

(x)

~

(x)

~

(ax +b)=

µ

4

µ

4

µ

4

(x).

E

−3

=

−3

=

−

3 = E

~2

(ax +b)

a

4

~2

(x)

µ

2

(x)

µ

2

µ

2

2

37. Метод условных вариантов для расчёта основных числовых характеристик вариационного ряда

Значения вариантов могут быть достаточно большими, и, следовательно, вычисление числовых характеристик достаточно трудоёмко. Поэтому для дискретного вариационного ряда при вычислении коэффициентов асимметрии и эксцесса желательно перейти к услов-

ным вариантам по формуле ui = xi h−C , где h- шаг вариационного

-55-

ряда, С- ложный ноль, то есть вариант, имеющий либо наибольшую частоту, либо равноудаленный от максимального и минимальных вариантов. Тогда основные числовые характеристики для вариантов x и

u	связаны	~	соотношениями x = hu +C ; S 2		(x)= h2S 2 (u) и
~	~		~	(u).
A(x)= A(u); E			(x)= E

Пример 39. Перейдя к условным вариантам, вычислить эмпирические коэффициенты асимметрии и эксцесса для интервального вариационного ряда.

Интервалы	[3 – 7)	[7 – 11)	[11 – 15)	[15 – 19)	[19 – 23)	[23 – 27)
Частоты	6	9	11	12	8		4	h=4.
Решение. Шаг интервального вариационного ряда равен
Если интервал имеет наибольшую частоту [15;19[, то за							условный

ноль примем его середину С=17. Перейдём к условным вариантам по

формуле u										=				xi −17								. Тогда получим дискретный вариационный ряд.
								i						4
ui				-3				-2					-1					0					1		2
mi				6					9					11							12		8		4	моменты:
Найдём эмпирические начальные
ν~		=		1 ∑u m							i			=	1				(−3 6 −2 9 −11+8 + 2 4)= − 31 = −0,62 ;
1				n				i						50										50
ν~		=		1 ∑u2m								i		=			1				((−3)2			6 +(−2)2 9 +(−1)2 11+8 + 22 2)=
2				n				i						50
=	125				= 2,5;
																				((−3)3 6 +(−2)3 9 +(−1)3 11+8 + 23 2)=
		50
ν~3 = n1 ∑ui3mi =																1
																50
= −			205				= −4,1;
		50																			((−3)4			6 +(−2)4 9 +(−1)4 11+8 + 24 2)=
ν~		=		1 ∑u4m								i		=			1
4				n				i						50

= 71350 =14,26.

Найдём эмпирические центральные моменты:

~	~	~2	2
µ2	=ν2	−ν1	= 2,5 − (− 0,62) = 2,1156;

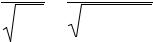
-56-

~	~	~ ~2	~3			3
µ3	=ν3	−3ν2ν1	+ 2ν1 = −4,1+3 2,5 0,62			+ 2(−0,62)	≈ −1,1554;
~	~	~ ~	~ ~2	~4	=14,26 + 4	4,1 0,62 +
µ4	=ν4	−4ν3ν1	+6ν2ν1	−3ν1

+6 2,5 (−0,62)2 −3 (−0,62)4 ≈ 7,1956.

Тогда среднее арифметическое равно

x = hu +C = hν~1 +C = 4 (−0,62)+17 =14,52.

Эмпирическая дисперсия равна

S	2	(x)= h	2	S	2	(u)= h	2	~	=16 2,1156 = 33,8496 .
								µ2

Эмпирический коэффициент асимметрии равен

~

~

−1,1554

=

µ

3

=

≈ −0,375.

A

2,11563

µ3

2

Эмпирический коэффициент эксцесса равен

~

~

7

,1956

µ

4

E

=

−3

=

−3

≈ −1,392.

~2

2,1156

2

µ

2

38. Статистическое оценивание параметров распределения

В самом общем смысле содержание этой темы можно сформулировать как совокупность методов, позволяющих делать научно обоснованные выводы о числовых параметрах распределения генеральной совокупности по случайной выборке из неё. Если, например, нас интересует математическое ожидание генеральной совокупности, то задача статистической оценки параметров заключается в том, чтобы найти такую выборочную характеристику, которая позволила бы получить по возможности более точное и надёжное представление об интересующем нас параметре (в данном случае о математическом ожидании). Состав выборки случаен, поэтому выводы о параметрах генеральной совокупности, сделанные по выборочным данным, могут быть ложными. С возрастанием числа элементов выборки вероятность правильного вывода увеличивается. Поэтому всякому решению, принимаемому при статистической оценке параметров, стараются поставить в соответствие вероятность, характеризующую степень достоверности принимаемого решения.

Сформулируем задачу оценки параметров в общем виде. Пусть X - случайная величина, подчиненная закону распределения

-57-

F (X ,Θ), где Θ - параметр распределения, числовое значение которо-

го неизвестно. Исследовать все элементы генеральной совокупности для вычисления параметра Θ не представляется возможным, поэтому об этом параметре пытаются судить по выборкам из генеральной совокупности.

Всякую однозначно определённую функцию результатов наблюдений, с помощью которой судят о значении параметра Θ , называют оценкой (или статистикой) параметра Θ . Рассмотрим некоторое множество выборок, объёмом п каждая. Выборочную оценку параметра Θ , вычисленную по i -й выборке, обозначим Θni . Так как

состав выборки случаен, то можно сказать, что Θni примет неизвест-

ное заранее числовое значение, то есть является случайной величиной.

Известно, что случайная величина определяется законом распределения и числовыми характеристиками, следовательно, и выборочную оценку можно также описывать законом распределения и числовыми характеристиками.

Для того чтобы отразить случайный характер выборки объёмом п из генеральной совокупности, обозначим её (X1, X2 ,K, Xn), а вы-

борочную оценку параметра Θ - через ~ . Следовательно, можно за-

Θn

писать ~n f (X1 , X2 ,K, Xn ). Выбор оценки, позволяющей полу-

Θ =

чить хорошее приближение оцениваемого параметра, – основная задача теории оценивания.

39. Основные свойства оценок

~

О.1. Оценку Θn параметра Θ называют несмещённой, если её

математическое ожидание равно оцениваемому параметру Θ , то есть

(~ ) ~

M Θn =Θ . Если это равенство не выполняется, то оценка Θn может

либо завышать значение Θ , либо занижать его. В обоих случаях это приводит к систематическим ошибкам в оценке параметра. Требование несмещённости гарантирует отсутствие систематических ошибок

при оценке параметров.

~

О.2. Несмещённую оценку Θn , которая имеет наименьшую

дисперсию среди всех несмещённых оценок параметра Θ , вычисленных по выборкам одного и того же объёма, называют эффективной

оценкой.

-58-

О.3. Оценку ~ параметра Θ называют состоятельной, если

Θn

она подчиняется закону больших чисел, то есть при достаточно

большом числе независимых наблюдений п с вероятностью, близкой

~

к единице, можно утверждать, что разность между Θn и Θ по абсо-

лютной величине окажется меньше сколь угодно малого числа τ , или
~	−η, где η- положительное число, близкое к нулю.
p{Θn −Θ <τ}>1

На практике при оценке параметров не всегда удаётся удовлетворить одновременно требованиям несмещённости, эффективности и состоятельности оценки. Так, например, может оказаться, что для простоты расчётов целесообразно использовать незначительно смещённую оценку. Однако выбору оценки всегда должно предшествовать её критическое рассмотрение со всех точек зрения.

40. Оценка математического ожидания и дисперсии Наиболее важными числовыми характеристиками случайной

величины являются математическое ожидание и дисперсия. Рассмотрим вопрос о том, какие выборочные характеристики лучше всего в смысле несмещённости, эффективности и состоятельности оценивают математическое ожидание и дисперсию.

Т.1. Средняя арифметическая x , вычисленная по п независимым наблюдениям над случайной величиной Х, которая имеет математическое ожидание µ, является несмещённой оценкой этого пара-

метра.

Доказательство. Пусть X1 , X2 ,K, Xn независимые наблюдения

										1	n
над случайной			величиной. По			определению			x =		∑Xi . Найдём
1		n		1 n						n i=1
						1
M(x)= M		∑Xi =			∑M(Xi )=			µn = µ.			Следовательно:
						n
n i=1				n i=1
M (x)= µ .

Т.2. Средняя арифметическая x , вычисленная по п независимым наблюдениям над случайной величиной, которая имеет матема-

тическое ожидание µ и дисперсию σ 2, является состоятельной оценкой этого параметра.

-59-

Доказательство. Вычислим

~

венство p{Θn −Θ <τ}>1−η, определяющее свойство состоятельно-

1 n

1

n

1

n

1

nσ 2

σ 2

D(x)= D

∑ Xi

=

∑D(Xi )=

∑σ 2 =

n2

=

n

.

n i=1

n2 i=1

n2 i=1

Запишем неравенство

Чебышева для

средней арифметической x ,

p{x −µ <τ}>1− D(x)

или

p{x −µ <τ}>1− σ 2

. При

достаточно

τ 2

σ 2

nτ 2

большом числе испытаний величина nτ2

является числом, близким

к нулю. Поэтому для сколь угодно малого числа τ

выполняется нера-

сти выборочных оценок.

Получение эффективных оценок - сложное дело. Приведём без доказательства важный для практики факт. Если случайная величина

Х распределена по нормальному закону с параметрами (µ,σ 2 ), то несмещённая оценка x математического ожидания µ имеет минималь-

ную дисперсию σ 2 n , поэтому средняя арифметическая x в этом

случае является эффективной оценкой математического ожидания µ.

Т.3. Если случайная выборка состоит из п независимых наблюдений над случайной величиной Х с математическим ожиданием µ и

дисперсией σ 2, то выборочная дисперсия S2	=	1	n
			∑(Xi − x)2
		n i=1

ляется несмещённой оценкой генеральной дисперсии.

			Доказательство.			По условию M (Xi )= µ				и D(Xi )=σ 2
				1	n	1	n		1	n
S 2		=			∑(Xi − x)2 =		∑((Xi	−µ)−(x −µ))2 =		∑(X i −µ)2 −
				n i =1		n i =1			n i =1
−	2	(x −µ)∑n (X i −µ)+(x −µ)2
	n
					i =1

не яв-

тогда