Е.Н. Грибанов Теория вероятностей и математическая статистика. Методические указания для студентов специальности 230500 - Социальный сервис и туризм

-60-

	n	n		2
Упростим выражение				=n(x −µ) ,
	(x −µ)∑(Xi −µ)=(x −µ) ∑Xi −nµ
	i=1	i=1

подставив полученное в выражение для эмпирической дисперсии по-

S2 =

1

∑n (Xi − µ)2 −

2

n(x − µ)2 +

(x − µ)2 =

1

∑n (Xi − µ)2 −

лучим

n i=1

n

n i=1

−(x − µ)2 .

1

n

2

2

2

σ

2

Но так как

M

∑(Xi

− µ)

=σ

и

M (x − µ)

= D(x)=

n

то

M (S

n i=1

2

2

1

n

2

2

2

σ

n −1

2

=σ

−

=

σ

. То

есть

)= M

∑(Xi − µ)

−(x − µ)

n

n

n i=1

S 2 является смещённой оценкой дисперсии генеральной совокупности.

Несмещённой оценкой дисперсии генеральной совокупности

	является S)2 =	1	n
			∑(Xi − x)2 . Обычно	эту		оценку называют ис-
		n −1 i=1			n
	правленной выборочной дисперсией. Дробь							называют поправкой
					n −1

Бесселя. Тогда имеем равенство S)2 = nn−1 S2 . При малых значениях

п поправка Бесселя довольно сильно отличается от единицы, с увеличением п она быстро стремится к единице. При n > 50 практически

нет разницы между S 2 и S)2 . Можно показать, что оценки S 2 и S)2 являются состоятельными оценками σ 2.

Несмещённой, состоятельной и эффективной оценкой σ 2 явля-

ется оценка S2 1 n (X )2 , для вычисления которой необходи-

x = n i∑=1 i − µ

мо знать математическое ожидание. Заметим, что оценка Sx2 эффективна лишь при условии нормальности распределения случайной ве-

личины Х в генеральной совокупности. Оценки S 2 и S)2 не являются эффективными. В том случае, когда значение математического ожи-

X1 , X2 ,K, Xn

-61-

дания неизвестно, то для оценки дисперсии σ 2 используют состоятельную и несмещённую оценку S)2 .

41. Метод максимального правдоподобия Основным способом получения оценок параметров генеральной

совокупности по данным выборке является метод максимального правдоподобия. Основная идея метода заключается в следующем.

Пусть X1 , X2 ,K, Xn - результаты независимых наблюдений над

случайной величиной Х, которая может быть как дискретной, так и непрерывной; f (X ,Θ)- вероятность значения (если случайная вели-

чина дискретна) и плотность вероятности (если случайная величина непрерывна). Функция f (X ,Θ) зависит от неизвестного параметра

Θ , который требуется оценить по выборке.

Если X1 , X2 ,K, Xn - независимые случайные величины, то

функцией	правдоподобия	называется	выражение
L = f (X1 ,Θ)f (X2 ,Θ)K f (Xn ,Θ).		В качестве оценки	неизвестного

параметраΘ берется такое значение Θ , при подстановке которого вместо параметра Θ получаем максимальное значение функции L.

Оценку Θ обычно называют оценкой максимального правдоподобия.

Оценка Θ зависит от количества и числовых значений случайных величин Xi , следовательно, сама является случайной величиной.

При максимизации функции L подразумевается, что значения фиксированы, а переменной является параметр Θ

(иными словами, максимум отыскивается в предположении, что Xi

заменены их числовыми значениями). Если Lдифференцируема относительно параметра Θ , то для отыскания максимума надо решить

уравнение ∂∂ΘL = 0 . В качестве оценки Θ выбрать решение, которое

обращает функцию L в максимум. Иногда удобно рассматривать уравнение ∂∂lnΘL = 0.

Согласно методу максимального правдоподобия для нормально распределенной генеральной совокупности в качестве оценок математического ожидания и дисперсии нужно брать соответственно

среднюю арифметическую и эмпирическую дисперсию S 2 .

-62-

Пример 40. Найти методом максимального правдоподобия по выборке X1 , X2 ,K, Xn точечную оценку неизвестного параметра λ

показательного распределения, плотность которого

f (x)= λe−λ x (x ≥ 0).

Решение.	Составим	функцию	правдоподобия
L = (λe−λX1 )(λe−λX2 )K(λe−λXn )= λne−λ∑ Xi .			Найдём логарифми-

ческую функцию правдоподобия ln L = n ln λ −λ∑ Xi . Найдём пер-

вую производную по λ

∂ln L = n

−∑ Xi .

Отсюда λ =

1

или

1

∂λ

λ

∑ Xi

∂2 ln L

n

1

. Так как

n

= −n(x)2 < 0

в силу положительности

λ =

∂λ2

= −

x

λ2

Xi то оценкой метода максимального правдоподобия параметра λ является величина, обратная среднему арифметическому.

42. Метод наименьших квадратов Изложенный ранее метод максимального правдоподобия всегда

приводит к состоятельным оценкам, хотя иногда смещённым. Известно, что этот метод использует наилучшим образом всю информацию о неизвестном параметре, содержащуюся в выборке. Однако часто его применение связано с необходимостью решения сложных систем уравнений.

Другим способом, имеющим большое практическое применение в задачах оценивания неизвестных параметров генеральной совокупности по выборке и часто приводящим к более простым выкладкам,

является метод наименьших квадратов.

Пусть, как и прежде, Х- случайная величина (дискретная или непрерывная) с законом распределения f (X ,Θ), (где Θ - неизвест-

ный параметр генеральной совокупности, который нужно оценить по выборке). X1 , X2 ,K, Xn - независимые наблюдения, Θ - оценка па-

раметра Θ , зависящая от количества наблюдений и их числовых значений.

Основная идея метода наименьших квадратов в приложении к оцениванию параметров сводится к тому, чтобы в качестве оценки неизвестного параметра принимать значение, которое минимизирует

-63-

сумму квадратов отклонений между оценкой и параметром для всех наблюдений. То есть находится минимум функции

n ( )( ))2

F = ∑ Θ −Θ Xi .

i=1

Если исходная случайная величина имеет нормальный закон распределения, то метод максимального правдоподобия и метод наименьших квадратов дают одинаковые результаты.

Особенно часто метод наименьших квадратов применяется в задачах выравнивания или сглаживания. Пусть в результате наблюдений получен ряд точек с координатами (x1; y1), (x2 ; y2 ),K,(xn ; yn ).

Если заранее известно, что зависимость между переменными имеет вид y = f x;a1;a2 , то необходимо определить числовые параметры

a1 ,a2 , которые наилучшим образом, в смысле наименьших квадратов, описывали бы зависимость, полученную при наблюдении. То

есть найти минимум функции F n (yi − f (xi ;a1;a2 ))2 . Для этого

= ∑

i =1

нужно решить систему уравнений

∂F = 0;∂a1

∂F = 0.∂a

2

Пример 41. Найти методом наименьших квадратов коэффициенты линейной зависимости y = ax +b по полученным эмпирическим

точкам с координатами (x1; y1), (x2 ; y2 ),K,(xn ; yn ).

n

Решение. Функция F имеет вид F = ∑(yi −axi −b)2 система

i=1

уравнений

∂F∂a

∂F∂b

n				−b)x			n				n
= −2 ∑(y	i	−ax	i		i	= 0;	∑ y	i	x	i	− a ∑
i=1							или i =1				i =1
n		−axi		−b)= 0.			n				n
= −2 ∑(yi							∑ yi		− a ∑xi
i=1							i =1				i =1

xi2	n
	− b ∑xi	= 0;
	i =1

− nb = 0.

-64-

	1		n	n
Выражая из второго уравнения b имеем b =			∑ yi −a ∑ xi , под-
	n i=1			i=1

n	n	n	n	n	2	=0. Отсю-
ставляя в первое получим n∑y x	−an∑x2	−∑x	∑y	+a ∑x
i i	i	i	i		i
i=1	i=1	i=1 i=1		i=1

	n		n		n
	n ∑yi xi		− ∑xi ∑yi
да a =	i=1		i=1		i=1	, подставляя полученное в выражение для b,
	n				2
				n
	n ∑ x2		−	∑x
	i=1	i			i
			i=1

находим его. Используя понятие средней арифметической результат можно записать гораздо компактней

a = xy − x y и b = y −ax . x2 −(x)2

43. Распределение средней арифметической для выборок из нормальной совокупности.

Распределение Стьюдента Выборочная средняя, вычисленная по конкретной выборке, есть

определённое число. Так как состав выборки случаен, то средняя арифметическая, вычисленная для элементов другой выборки того же объёма из той же генеральной совокупности, определяется числом, как правило, отличным от первого, то есть средняя меняется от выборки к выборке.

Следовательно, выборочную среднюю можно рассматривать как случайную величину, что позволяет говорить о законе распределения выборочной средней. Приведём без доказательства следующую теорему.

Т. Если случайная величина Х подчиняется нормальному закону распределения с параметрами (µ,σ 2 ), а X1 , X2 ,K, Xn - ряд незави-

симых наблюдений над случайной величиной Х, каждое из которых имеет те же характеристики, что Х, то выборочная средняя

					-65-
	1	n
x =		∑ Xi также подчиняется нормальному закону распределения с
	n i=1			2
			µ,σ
параметрами				.
				n	(x − µ)
	Нормированное отклонение					n	подчиняется нормально-
					σ

му закону распределения со средним значением, равным нулю, и дисперсией, равной единице. Действительно, используя свойства математического ожидания, а также тот факт, что x и µ независимы,

имеем:

(x - µ)

n

n

n

=

(M (x)− µ)=

(µ − µ)= 0 и

M

σ

σ

σ

2

(x − µ)

n

n

(D(x)+ D(µ))=

n

σ

=1.

D

σ

=

σ

2

n

σ 2

Пример 42. Автомат штампует детали. Контролируется длина детали которая подчиняется нормальному закону распределения. Найти вероятность того, что средняя длина x деталей, отобранных случайным образом, отклонится от математического ожидания более

чем на 2 мм, если дисперсия случайной величины Х равна σ 2 = 9 мм2, а количество деталей в выборке п=16.

Решение. Случайная величина Х имеет нормальное распределе-

ние с математическим ожиданием

2

σ 2

9

µ и дисперсией σ x

=

n

=

или

16

3

σ x =

.

Найдём вероятность

того, что при

x − µ

< 2

она

равна

4

2

8

p{

x − µ

= 2Ф

= 0,9982 ,

следовательно:

< 2}= 2Ф

σ x

3

p{x − µ ≥ 2}=1−0,9982 = 0,078, то есть практически можно быть

уверенным, что наблюдаемая средняя длина детали отклонится от заданной не более чем 2 мм.

Итак, если случайная величина Х имеет нормальное распреде-

ление, то нормированное отклонение (x − µ) n также подчиняется

σ

-66-

нормальному закону распределения. Однако дисперсия генеральной

совокупности σ 2 почти всегда оказывается неизвестной, поэтому вызывает большой практический интерес изучение распределения

статистики t = (x −)µ) n , где S)2 - несмещенная и состоятельная

S 2

оценка дисперсии, вычисленная по выборочным данным. Распределение статистики t не зависит ни от математического ожидания µ

случайной величины Х, ни от дисперсии σ 2, а лишь зависит от объёма выборки п. Закон распределения статистики t называют распределением Стьюдента. Распределение Стьюдента табулировано во всех учебниках по математической статистике.

Из анализа распределения Стьюдента при п>50 видно, что оно мало отличается от нормального.

44. Распределение дисперсии в выборках из нормальной генеральной совокупности.

Распределение 2 Пирсона Рассмотрим закон распределения выборочной дисперсии, рас-

считанной для наблюдений, взятых из нормальной генеральной совокупности. Так как состав выборки подвержен случайности, то выборочную дисперсию, как и x , следует рассматривать как случайную величину и говорить о законе распределения выборочной дисперсии. При анализе распределения выборки следует иметь в виду два случая: 1) математическое ожидание случайной величины известно; 2) математическое ожидание неизвестно.

Случай 1. Предположим, что математическое ожидание случайной величины известно. Условимся считать, что случайная величина

Хподчиняется нормальному закону распределения с параметрами

µ,σ 2 , а X1 , X2 ,K, Xn - ряд независимых наблюдений, каждое из которых подчиняется нормальному закону распределения с математи-

ческим ожиданием µ и дисперсией σ 2. Тогда выборочная дисперсия

			1	n
	вычисляется по формуле	Sx2 =		∑(Xi − µ)2 .	Разделим обе	части
		σ 2	n i=1
	этого равенства на			и умножим	на п.	Имеем

											-67-
	nS 2		n				X	i	− µ 2		n
	x	= ∑									= ∑ti2 . Статистика t имеет нормальный закон
	σ 2							σ
			i=1								i=1
распределения										с	параметрами M (t )= 0 и D(t )=1. Пусть
		2						n
2 =			nS x			= ∑ti2 .
			σ 2
							i=1

Случайная величина, представляющая собой сумму квадратов независимых случайных величин, каждая из которых подчиняется

нормальному закону распределения с параметрами (µ = 0,σ 2 =1), на-

зывается случайной величиной с распределением 2 и k = n степеня-

ми свободы.

Распределение статистики 2 не зависит ни от математического

ожидания µ случайной величины Х, ни от дисперсии σ 2, а зависит лишь от объёма выборки п. Найдём математическое ожидание рас-

пределения 2 :

M ( 2 )= M n ti2 =

∑

i=1

n	n	X		i	− µ 2			1		n
∑M (ti2 )= ∑M							=			∑σ 2 = n.
				σ
i=1	i=1							σ 2 i=1

Следовательно, математическое ожидание случайной величины

с распределением 2 и k = n степенями свободы равно числу степеней свободы. В специальной литературе можно найти доказательство

того, что дисперсия распределения 2 равна удвоенному числу сте-

пеней свободы. Дифференциальная функция распределения 2 сложна, и интегрирование её является весьма трудоёмким процессом,

поэтому составлены таблицы распределения 2 .

Случай 2. Рассмотрим закон распределения выборочной дисперсии, когда математическое ожидание случайной величины неизвестно. Как и прежде, случайная величина подчиняется нормальному за-

кону распределения с параметрами µ,σ 2 , а X1 , X2 ,K, Xn - ряд не-

зависимых наблюдений, каждое из которых подчиняется нормальному закону распределения с математическим ожиданием µ и диспер-

сией σ 2. Тогда дисперсия выборки вычисляется по формуле

					-68-
	S)2 =	1		n	(Xi − x)2 . Примем без доказательства тот факт, что слу-
				∑
			n −1 i=1
					)2
	чайная величина					nS	имеет распределение 2 с k = n −1 степенями
						σ 2
	свободы.
					45. Понятие доверительного интервала.
						Доверительная вероятность
		Оценку неизвестного параметра генеральной совокупности од-

ним числом называют точечной оценкой. Наряду с точечным оцениванием статистическая теория занимается вопросами интервального оценивания. Задачу интервального оценивания в самом общем случае можно сформулировать так: по данным выборки построить числовой интервал, относительно которого с заранее выбранной точностью можно сказать, что внутри находится числовой параметр. Интервальное оценивание особенно необходимо при малом числе наблюде-

ний, когда точечная оценка мало надёжна.

[~(1) ~(2)]

О.1. Доверительным интервалом Θn ;Θn для параметра Θ

называют такой интервал, относительно которого можно с заранее выбранной вероятностью p =1 −α , близкой к единице, утверждать,

что	содержит неизвестное значение параметра Θ , то	есть
~	~
p{Θn(1) <Θ <Θn(2)}=1−α .		~(1)
	~(2)		,
	Чем меньше для выбранной вероятности разность Θn	−Θn

тем точнее оценка неизвестного параметра Θ , и на оборот, если этот

интервал велик, то оценка, произведенная с его помощью, мало при-
~(1)	~(2)	за-
годна для практики. Концы доверительного интервала Θn	и Θn

висят от элементов выборки, поэтому их значения могут меняться от выборки к выборке. Вероятность p =1−α принято называть довери-

тельной вероятностью, а число α - уровнем значимости.

46. Доверительный интервал для математического ожидания при известной дисперсии генеральной совокупности Пусть случайная величина Х распределена нормально, причём

среднее квадратическое отклонение σ этого распределения известно.

-69-

Требуется построить доверительный интервал для неизвестного математического ожидания µ с заданным уровнем значимости α . Ранее

показано, что выборочное среднее распределено нормально с пара-

метрами

(x − µ)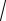n

σ

M (x −σµ)

отклонения

M (x)=

µ, D(x)=

σ 2

,

нормированное

отклонение

n

распределено

также

нормально с

параметрами

n

− µ)

n

= 0 и

(x

=1. Поэтому вероятность любого

D

σ

x − µ

может

быть

вычислена

по формуле

p (x − µ)

n < zкр = 2Ф(zкр). Для заданной доверительной вероят-

σ

или Ф(zкр)=

ности имеем p =1−α = 2Ф(zкр)

1−α

затем по таблице

2

функции Ф(х) находим zкр. Преобразуем формулу к удобному виду

z

σ

p x

− µ <

кр

= 2Ф(zкр)или

σ z

n

σ z

кр

− x <

кр

= 2Ф(zкр),

p −

< µ

n

n

+σ zкр

откуда p x −σ zкр < µ

< x

= 2Ф(zкр).

n

n

Таким образом, с вероятностью (надёжностью) 1−α можно ут-

верждать,

что интервал

z

σ

z

σ

x −

кр

; x +

кр

является доверитель-

n

n

ным для оценки математического ожидания.

Пример 43. Случайная величина Х имеет нормальное распределение с известным средним квадратическим отклонением σ =12. Найти доверительный интервал для оценки математического ожидания µ по выборочной средней x = 45 , если объём выборки n = 36 и

доверительная вероятность p = 0,95.

Решение. Используя соотношение Ф(zкр)=1−2α =0,295=0,475,