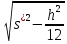Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Сибирский государственный индустриальный университет»
Кафедра техногенных и вторичных ресурсов
УТВЕРЖДАЮ
Зав. кафедрой техногенных и
вторичных ресурсов
проф., д.т.н.
___________ Е.П. Волынкина «___»______ 2012 г
КОНСПЕКТ ЛЕКЦИЙ
УЧЕБНОЙ ДИСЦИПЛИНЫ
«Планирование эксперимента и математическая статистика»
для специальности 150109
«Металлургия техногенных и вторичных ресурсов»
Составил:
доцент, к.т.н. Л.А. Самигулина
Новокузнецк
2012
СОДЕРЖАНИЕ
Введение.
Лекция 1. Классификация ошибок измерения.
Лекция 2. Распределение случайных ошибок измерения.
Лекция 3. Методы исключения грубых ошибок.
Лекция 4. Средние значения, методы их вычисления.
Лекция 5. Оценки истинного значения измеряемой величины.
Лекция 6. Сравнение средних значений.
Лекция 7. Оценки точности измерений.
Лекция 8. Сравнение дисперсий.
Лекция 9. Проверка нормальности распределения.
Лекция 10. Основные понятия планирования эксперимента.
Лекция 11. Общие требования к плану эксперимента. О критериях планирования эксперимента.
Лекция 12. Планы для моделей, описываемых полиномами первого порядка.
Лекция 13. Планы для моделей, содержащих линейные члены и взаимодействия различного порядка.
Лекция 14. Планы для квадратичных моделей.
Лекция
Введение.
Общие представления о методах статистической обработки экспериментальных данных, методах планирования эксперимента.
В курсе теории вероятностей изучаются закономерности случайных явлений. Отправной точкой при этом является вероятностная модель случайного явления (Q, F, P), где Q - пространство элементарных событий рассматриваемого явления, F - ст-алгебра наблюдаемых событий и P - вероятностная мера на ней, которая предполагается известной. Однако, на практике почти всегда приходится сталкиваться со случайными явлениями, в которых вероятностная мера неизвестна. Возникает вопрос, можно ли, и если можно, то каким образом исследовать закономерности случайных явлений в этих ситуациях?
Положительный ответ на поставленный вопрос дает математическая статистика; эта дисциплина занимается разработкой научно обоснованных методов исследования закономерностей случайных явлений в случаях, когда вероятностная мера заранее неизвестна. Таким образом, математическая статистика является инструментом измерения вероятностей, а ее задачи - в некотором смысле обратными по отношению к задачам теории вероятностей.
Решение этих задач строятся на основе обработки статистических данных, которые получаются путем проведения активного или пассивного эксперимента над исследуемым явлением. В связи с этим возникает второй вопрос: как организовать (если это возможно) проведение эксперимента наилучшим, в некотором смысле, образом, например, с наименьшими затратами? Решением этих вопросов занимается раздел математической статистики, который носит название планирование эксперимента.
Итак, математическая статистика занимается изучением случайных явлений в условиях неопределенности вероятностной модели, планирование эксперимента решает задачу наилучшей, в некотором смысле, организации эксперимента.
В настоящее время математическую статистику можно определить как науку о принятии решений в условиях неопределенности.
Статистические выводы относятся к процессу получения какого-либо заключения относительно генеральной совокупности по свойствам выборки из этой совокупности. Обычно совокупность характеризуется одним или несколькими параметрами. Параметры генеральной совокупности будем обозначать греческими буквами, например, μ — среднее совокупности, σ 2 — дисперсия совокупности, σ2 — среднее квадратическое отклонение совокупности. Величины, вычисленные по выборочным значениям, взятым из совокупности, называются оценками, выборочными статистиками или просто статистиками.
Математическая статистика основывается на допущении, что выборки, взятые из генеральной совокупности, являются случайными, т. е. каждый элемент совокупности может с одинаковой вероятностью оказаться включенным в выборку, и что извлечение п элементов не влияет на модель изменчивости совокупности.
Понятие статистического вывода можно разделить на две части:
1) оценка параметров генеральной совокупности
2) проверка статистических гипотез.
Лекция 1
Классификация ошибок измерения.
Грубые ошибки. Систематические ошибки. Случайные ошибки.
Численное значение физической величины получается в результате ее измерения, т.е. сравнения ее с другой величиной того же рода, принятой за единицу. При выбранной системе единиц результаты измерений выражаются определенными числами. Известно, что при достаточно точных измерениях одной и то же величины результаты отдельных измерений отличаются друг от друга, и, следовательно, содержат ошибки.
Ошибкой измерения называется разность x - a между результатом измерения x и истинным значением a измеренной величины. Ошибка измерения обычно неизвестна, как неизвестно и истинное значение измеряемой величины (исключения составляют измерения известных величин, проведенные со специальной целью исследования ошибок измерения, например для определения точности измерительных приборов). Одной из основных задач математической обработки результатов эксперимента как раз и является оценка истинного значения измеряемой величины по получаемым результатам. Другими словами, после неоднократного измерения величины a и получения ряда результатов, каждый из которых содержит некоторую неизвестную ошибку, ставиться задача вычисления приближенного значения a с возможно меньшей ошибкой. Для решения этой задачи ( при данном уровне точности измерения) надо знать основные свойства ошибок измерений и уметь ими воспользоваться.
Грубые ошибки. Прежде всего, при математической обработке результатов измерений не следует учитывать заведомо неверные результаты (промахи), или, как говорят, результаты, содержащие грубые ошибки. Грубые ошибки возникают вследствие нарушения основных условий измерения или в результате недосмотра экспериментатора (например, при плохом освещении вместо «3» записывают «8»). При обнаружении грубой ошибки результат измерения следует сразу отбросить, а само измерение повторить(если это возможно). Внешним признаком результата, содержащего грубую ошибку, является его резкое отличие по величине от результатов остальных измерений. На этом основаны некоторые критерии исключения грубых ошибок по их величине, однако самым надежным и эффективным способом браковки неверных результатов остается браковка их непосредственно в процессе самих измерений. Всюду в настоящем справочном руководстве считается, что оставленные для математической обработки результаты измерений не содержат грубых ошибок.
Систематические ошибки. Ошибки измерения вызываются большим количеством разнообразных причин (факторов). Иногда в проведенной серии измерений удается выделить такие причины ошибок, эффект действия которых может быть рассчитан. Например, если после измерений обнаружена неправильная регулировка приборов, которая привела к смещению начала отсчета, то все снятые показания будут смещены либо на постоянную величину, если шкала прибора равномерна, либо на величину, изменяющуюся по определенному закону, если шкала прибора неравномерна. Другим примером может служить изменение внешних условий, например, температуры, если известно влияние этих изменений на результаты измерений. К названным причинам можно также отнести некоторое несовершенство измерительных приборов на границе области их применимости, вызывающее известных ошибок.
Принято говорить, что каждая из таких причин вызывает систематическую ошибку. Выявление систематических ошибок, вызываемых каждым отдельным фактором, требует специальных исследований (например, измерений одной и той же величины разными методами или измерений одним и тем же прибором некоторых эталонов, известных величин). Но как только систематические ошибки обнаружены и их величины рассчитаны, они могут быть легко устранены путем введения соответствующих поправок в результате измерения. Поэтому в настоящем справочном руководстве мы будем считать, что к началу математической обработки результатов измерений все систематические ошибки уже выявлены и устранены. Подчеркнем, что при этом общая ошибка каждого результата остается неизвестной, так что речь идет не о выделении из общей ошибки некоторой части в виде систематической ошибки, а лишь о введении поправок на известный эффект действия тех факторов, которые удалось выявить.
Случайные ошибки. Ошибки измерения, остающиеся после устранения всех выявленных систематических ошибок, т.е. ошибки результатов измерений, исправленных путем введения соответствующих поправок, называются случайными. Случайные ошибки вызываются большим количеством таких факторов, эффекты действия которых столь незначительны, что их нельзя выделить и учесть в отдельности (при данном уровне техники и точности измерений). Случайную ошибку можно рассматривать как суммарный эффект действия таких факторов.
Случайные ошибки являются неустранимыми, их нельзя исключить в каждом из результатов измерений. Но с помощью методов теории вероятности можно учесть их влияние на оценку истинного значения измеряемой величины, что позволяет определить значение измеряемой величины со значительно меньшей ошибкой, чем ошибки отдельных измерений. Учет влияния случайных ошибок основан на знании законов их распределения.
Лекция 2
Распределение случайных ошибок измерения.
Вероятностная модель. Нормальный закон распределения. Показатели точности измерения.
Вероятностная
модель. Случайные
ошибки измерения характеризуются
определенным законом их распределения.
Существование такого закона можно
обнаружить, повторяя много раз в
неизменных условиях измерение некоторых
величины и подсчитывая число m
тех результатов измерения, которые в
любой выделенный (отмеченный) интервал:
отношение этого числа к общему числу n
произведенных
измерений (относительная
частота попадания в отмеченный интервал)
при достаточно большом числе измерений
оказывается близким к постоянному числу
(разумеется, своему для каждого интервала).
Это обстоятельство позволяет применить
к изучению случайных ошибок измерения
методы теории вероятности. В
теоретико-вероятностной модели случайные
ошибки
z
= x
- a
(а
значит, и сами результаты измерения x
= a
- z)
рассматриваются как случайные
величины,
которые могут принимать любые
действительные значения, причем каждому
интервалу ( )
соответствует вполне определенное
число, называемое вероятностью
попадания случайной величины z
в этот интервал и
обозначаемое через Р(
)
соответствует вполне определенное
число, называемое вероятностью
попадания случайной величины z
в этот интервал и
обозначаемое через Р( <
z
<
<
z
<
 )
или
)
или
Р(z
Є ( )).
Эта вероятность выступает как
идеализированная относительная частота
попадания в интервал (
)).
Эта вероятность выступает как
идеализированная относительная частота
попадания в интервал (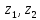 ),
т.е. на практике именно к этой вероятности
близки упомянутые выше относительные
частоты:
),
т.е. на практике именно к этой вероятности
близки упомянутые выше относительные
частоты:
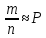 (
(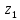 <
z
<
<
z
<
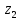 ).
).
Правило,
позволяющее для любых интервалов ( )
находить вероятности Р(
)
находить вероятности Р(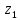 <
z
<
<
z
<
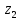 ),
называются законом
распределения вероятностей случайной
величины z.
Во
всех задачах, рассматриваемых в настоящем
справочном руководстве, закон распределения
записывается с помощью интеграла
),
называются законом
распределения вероятностей случайной
величины z.
Во
всех задачах, рассматриваемых в настоящем
справочном руководстве, закон распределения
записывается с помощью интеграла
 <
z <
<
z <
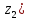 =
=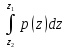 ,
(1)
,
(1)
где p(z) – некоторая неотрицательная функция, нормированная условием
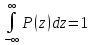 ;
;
эта функция полностью определяет соответствующий закон распределения вероятностей и называется плотностью распределения.
Нормальный закон распределения. В качестве закона распределения случайных ошибок измерения чаще всего принимают нормальный закон распределения ( закон Гаусса). Плотность нормального распределения равна
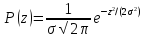 ,
(2)
,
(2)
где
параметр
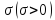 характеризует точность измерений.
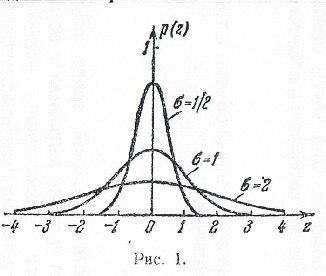
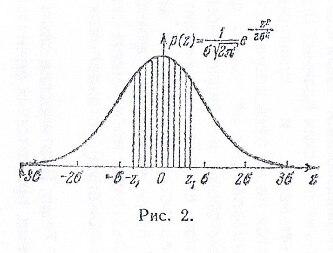
График плотности распределения
вероятностей называется кривой
распределения.
На рис.1 показаны кривые
нормального распределения
при различных значениях
характеризует точность измерений.
График плотности распределения
вероятностей называется кривой
распределения.
На рис.1 показаны кривые
нормального распределения
при различных значениях
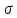 ;
из этого рисунка видно, что при уменьшении
параметра
;
из этого рисунка видно, что при уменьшении
параметра
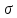 кривая нормального распределения
сжимается вдоль оси Oz
и вытягивается вдоль оси p(z);
и, следовательно, чем меньше
кривая нормального распределения
сжимается вдоль оси Oz
и вытягивается вдоль оси p(z);
и, следовательно, чем меньше
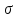 ,
тем быстрее убывает плотность распределения
p(z)
с возрастанием
,
тем быстрее убывает плотность распределения
p(z)
с возрастанием
 .
.
Вероятность
(2) попадания в интервал
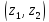 графически изображается площадью
соответствующей криволинейной трапеции
под кривой распределения вероятностей.
В частности, вероятность попадания в
симметричный
интервал
графически изображается площадью
соответствующей криволинейной трапеции
под кривой распределения вероятностей.
В частности, вероятность попадания в
симметричный
интервал
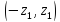
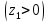 изображается площадью фигуры,
заштрихованной на рис. 2. Отсюда также
видно, что чем меньше
изображается площадью фигуры,
заштрихованной на рис. 2. Отсюда также
видно, что чем меньше
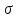 ,
тем меньше разброс ошибок около нуля.
,
тем меньше разброс ошибок около нуля.
Вероятность
попадания случайной ошибки в симметричный
интервал
 при нормальном распределении вычисляется
по формуле
при нормальном распределении вычисляется
по формуле
 ,
(3)
,
(3)
где
 (t
> 0). (4)
(t
> 0). (4)
Функция Ф(t) называется интегралом вероятностей, ее значения приведены в специальных таблицах. В этой таблице значения Ф(t) приведены лишь для положительных значений аргумента; для отрицательных значений аргумента функция Ф(t) продолжается нечетным образом:
Ф(t)=-Ф(t).
Вероятность
попадания случайной ошибки в любой
интервал
 в случае нормального распределения
вычисляется по формуле
в случае нормального распределения
вычисляется по формуле
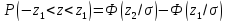 .
(5)
.
(5)
Наконец,
вероятность того, что случайная ошибка
выйдет за границы
 ,
равна
,
равна
 .
(6)
.
(6)
Для
удобства расчетов значения вероятностей
1-2Ф(t)
при значения t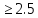 приведены в таблице Там же даны значения
и обратной функции t
= t(
приведены в таблице Там же даны значения
и обратной функции t
= t(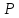 ),
для которой 1-
),
для которой 1-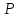 =1-2Ф(t),
т.е.
=1-2Ф(t),
т.е.
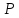 =
2Ф(t).
При больших значениях t
вероятность (6) очень мала. Например,
=
2Ф(t).
При больших значениях t
вероятность (6) очень мала. Например,
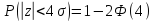 =6
=6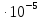 ,
,
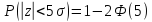 =6
=6 .
Уже вроятность выхода за трехсигмовые
пределы
.
Уже вроятность выхода за трехсигмовые
пределы
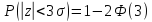 =0,0027
(7)
=0,0027
(7)
настолько
мала, что выход случайной ошибки измерения
за трехсигмовые пределы считают
практически невозможным (правило
трех сигм).
Другими словами, принимается, что
случайные ошибки измерения ограничены
по абсолютной величине значением
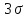 (хотя рассматриваемая математическая
модель допускает в принципе любые
значения ошибок).
(хотя рассматриваемая математическая
модель допускает в принципе любые
значения ошибок).
Нормальный закон распределения случайных ошибок обычно достаточно хорошо согласуется с опытом, что может быть проверено путем измерений известных величин (эталонов), когда можно точно подсчитать величины ошибок. В частности, нормальный закон отражает известное свойство симметрии случайных ошибок (случайные ошибки разных знаков встречаются примерно одинаково часто) и свойство концентрации (малые по абсолютной величине случайные ошибки встречаются чаще, чем большие).
Если в некоторой задаче возникает сомнение в нормальности закона распределения случайных ошибок (например, если случайные ошибки выходят за трехсигмовые пределы или если нарушается симметрия их распределения), то результаты измерения следует подвергнуть обработке.
Если
случайные ошибки
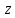 имеют нормальный закон распределения
с плотностью (2), то распределение
результатов измерения x
= a+z
имеет плотность,
имеют нормальный закон распределения
с плотностью (2), то распределение
результатов измерения x
= a+z
имеет плотность,
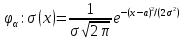 ,
(8)
,
(8)
которая
только сдвигом на величину a
отличается
от плотности (2). Этот закон распределения
называется общим
нормальным законом с центром a.
Плотность (2) может быть записана, как
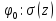 .
Для случайных ошибок всегда предполагается,
что центр их распределения равен нулю.
.
Для случайных ошибок всегда предполагается,
что центр их распределения равен нулю.
Показатели
точности измерения. Параметр
 («сигма») называется средней квадратической
ошибкой измерения, стандартной ошибкой
или просто стандартом. Квадрат величины
(«сигма») называется средней квадратической
ошибкой измерения, стандартной ошибкой
или просто стандартом. Квадрат величины
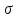 называется дисперсией ошибки. Связь
дисперсии с распределением вероятностей
указана (4).
называется дисперсией ошибки. Связь
дисперсии с распределением вероятностей
указана (4).
Кроме названных, иногда применяются и другие показатели точности измерений. Соотношения между различными показателями точности в случае нормального распределения ошибок следующие:
Вероятная ошибка
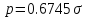 ,
2Ф
,
2Ф (9)
(9)
Средняя абсолютная ошибка
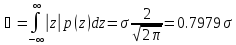 (10)
(10)
Мера точности
 .
(11)
.
(11)
Лекция 3
Методы исключения грубых ошибок. Метод исключения при известной σ. Метод исключения при неизвестной σ.
При получении результата измерения, резко отличающегося от всех других результатов, естественно возникает подозрение, что допущена грубая ошибка. В этом случае необходимо сразу же проверить, не нарушены ли основные условия измерения.
Если же такая проверка не была сделана вовремя, то вопрос о целесообразности браковки одного «выскакивающего» значения решается путем сравнения его с остальными результатами измерения. При этом применяются различные критерии, в зависимости от того, известна или нет средняя квадратическая ошибка σ измерений (предполагается, что все измерения производятся с одной и той же точностью и независимо друг от друга).
Метод исключения при известной σ. Обозначим «выскакивающее» значение через х* а все остальные результаты измерения через х1 х2, …хп. Подсчитаем среднее арифметическое значение
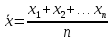
и
сравним абсолютную величину разности
х*
с величиной
 Для
полученного отношения
Для
полученного отношения
 ,
(1)
,
(1)
подсчитаем вероятность 1—2Ф(t) с помощью (Приложение, стр. 172). Это даст вероятность того, что рассматриваемое отношение случайно примет значение, не меньшее чем t, при условии, что значение х* не содержит грубой ошибки (что ошибка результата х* только случайна). Если подсчитанная указанным образом вероятность окажется очень малой, то «выскакивающее» значение содержит грубую ошибку и его следует исключить из дальнейшей обработки результатов измерений.
Какую именно вероятность считать очень малой, зависит от конкретных условий решаемой задачи: если назначить слишком низкий уровень малых вероятностей, то грубые ошибки могут остаться, если же взять этот уровень неоправданно большим, то можно исключить результаты со случайными ошибками, необходимые для правильной обработки результатов измерения. Обычно применяют один из трех уровней малых вероятностей:
5 % - уровень (исключаются ошибки, вероятность появления которых меньше 0,05);
1 % уровень (исключаются ошибки, вероятность появления которых меньше 0,01);
0,1% уровень (исключаются ошибки, вероятность появления которых меньше 0,001).
При
выбранном уровне α малых вероятностей
«выскакивающее» значение х*
считают содержащим грубую ошибку, если
для соответствующего отношения
t
(1) вероятность 1 - 2Ф(t)
< α. Чтобы подчеркнуть вероятностный
характер этого заключения, говорят, что
значение Х* содержит грубую ошибку
с надежностью вывода
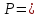 1
- α. Значение
t
= t(
1
- α. Значение
t
= t( ),
для которого 1- 2Ф(t) = α и,
значит,
2Ф(t)
=
),
для которого 1- 2Ф(t) = α и,
значит,
2Ф(t)
=
 ,
называется
критическим значением отношения
(1) при надежности
,
называется
критическим значением отношения
(1) при надежности
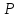 .
Так, если α = 0,01 (1% уровень), то
.
Так, если α = 0,01 (1% уровень), то
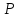 = 0,99, критическое значение t
= t(
= 0,99, критическое значение t
= t(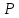 )
= 2,576 (прилож
II), и как только отношение (1) превзойдет
это критическое значение, мы можем
браковать «выскакивающее» значение х*
с надежностью вывода 0,99.
)
= 2,576 (прилож
II), и как только отношение (1) превзойдет
это критическое значение, мы можем
браковать «выскакивающее» значение х*
с надежностью вывода 0,99.
Пример.
Пусть среди 41 результата независимых
измерений, произведенных со средней
квадратической ошибкой α = 0,133, обнаружено
одно «выскакивающее» значение х*
= 6,866, в то время как среднее из остальных
40 результатов составляет
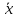 = 6,500, Можно ли считать, что «выскакивающее»
значение содержит грубую ошибку, и
исключить его из дальнейшей обработки?
= 6,500, Можно ли считать, что «выскакивающее»
значение содержит грубую ошибку, и
исключить его из дальнейшей обработки?
Решение.
Разность между «выскакивающим» значением
и средним составляет x*
-
 = 0,366, поэтому отношение (1) равно
= 0,366, поэтому отношение (1) равно
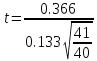 =
2.72
=
2.72
По (прилож. II) для t = 2,72 оцениваем вероятность 1 --2Ф (t) = 0,0066
<
0,007. Следовательно, с надежностью вывода
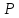 > 0,993 можно считать, что значение
содержит грубую ошибку, и исключить это
значение из дальнейшей обработки
результатов измерения.
> 0,993 можно считать, что значение
содержит грубую ошибку, и исключить это
значение из дальнейшей обработки
результатов измерения.
Подчеркнем, что указанный прием применяется только тогда, когда величина о средней квадратической ошибки точно известна заранее.
Метод исключения при неизвестной σ. Если величина σ заранее неизвестна, то она оценивается приближенно по результатам измерений, т. е. вместо нее применяют эмпирический стандарт
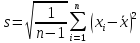 ,
(2)
,
(2)
При
этом абсолютную величину разности
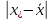 между
«выскакивающим» значением x*
и средним значением
между
«выскакивающим» значением x*
и средним значением
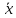 остальных
(приемлемых) результатов делят на
эмпирический стандарт и полученное
отношение
остальных
(приемлемых) результатов делят на
эмпирический стандарт и полученное
отношение
t
=
 s (2)
s (2)
сравнивают
с критическими значениями
tn( )
из (прилож. стр. 173). Если при данном числе
n
приемлемых результатов отношение (2)
оказывается между двумя критическими
значениями при надежностях
)
из (прилож. стр. 173). Если при данном числе
n
приемлемых результатов отношение (2)
оказывается между двумя критическими
значениями при надежностях
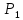 и
и
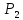 (
(
 то
с надежностью вывода, большей
то
с надежностью вывода, большей
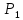 можно считать, что «выскакивающее»
значение содержит грубую ошибку, и:
исключить его из дальнейшей обработки
результатов.
можно считать, что «выскакивающее»
значение содержит грубую ошибку, и:
исключить его из дальнейшей обработки
результатов.
Заметим, что если надежность вывода окажется недостаточной, то это свидетельствует не об отсутствии грубой ошибки, а лишь об отсутствии достаточных оснований для исключения «выскакивающего» значения.
Пример. Пусть для п результатов независимых равноточных измерений некоторой величины среднее значение равно x* = 6,500, а эмпирический стандарт s = 0,133, и пусть (n + 1)-е измерение дало результат x* = 6,866. Можно ли исключить этот результат из дальнейшей обработки?
Решение.
Здесь отношение (2) равно
t
=
0,366/0,133 = 2,75. Если число приемлемых
результатов n
== 40, то полученное отношение превосходит
критическое значение 2,742 при надежности
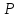 = 0,99 и значение x*можно
исключить с надежностью вывода, большей
0,99. Если же число приемлемых результатов
п
=
6, то полученное отношение меньше
критического значения 2,78 даже при
надежности
= 0,99 и значение x*можно
исключить с надежностью вывода, большей
0,99. Если же число приемлемых результатов
п
=
6, то полученное отношение меньше
критического значения 2,78 даже при
надежности
 =0,95 и значение x*,
исключать не следует.
=0,95 и значение x*,
исключать не следует.
Лекция 4
Средние значения, методы их вычисления.
Вычисление средних значений. Вычисление средних значений для интервального ряда данных. Теоретические средние значения (моменты распределения).
Любой эксперимент, связанный с измерением величин, сопровождается погрешностями измерений, вносящими элемент неопределенности в результат эксперимента. В связи с этим порядок проведения опытов должен быть выбран таким, чтобы имелась возможность оценить случайную ошибку эксперимента и избежать влияния возможных систематических ошибок. Постановка повторных или параллельных опытов полностью не исключает неопределенность, так как они проводятся также с погрешностью воспроизводимости. Выделить ошибку эксперимента, оцениваемую с помощью дисперсии ошибки, возможно только при дублировании опытов повторением m раз каждой строки матрицы планирования.
Сделать случайными мешающие факторы, действие которых может иметь систематический характер, позволяет принцип рандомизации, применяемый при реализации матрицы планирования эксперимента.
Перед проведением опытов на объекте следует определить возможные факторы, мешающие исследованию, и провести рандомизацию порядка проведения опытов с тем, чтобы эти факторы влияли на результаты эксперимента случайным образом.
Рандомизацию следует проводить следующим образом: в таблице равномерно распределенных случайных чисел выбирается некоторый столбец, из которого в порядке их следования берутся числа от 1 до 4m и записываются в столбцы, определяющие порядок следования опытов kim матрицы планирования. Пусть, например, при i=2 k21=4. Это значит, что вторая строка варьирования реализуется четвертой по порядку. При этом мешающий фактор при случайном порядке проведения опытов не будет вызывать систематической ошибки.
Например, для двухфакторного эксперимента
|
№ опы та |
Порядок проведения |
Матрица планирования |
Результаты проведения |
|||||||||||||||||
|
i |
ki1 |
ki2 |
… |
kil |
… |
kim |
x0 |
x1 |
x2 |
x1 x2 |
yi1 |
yi2 |
… |
yil |
… |
yim |
|
|
||
|
1 |
k11 |
k12 |
… |
k1l |
… |
k1m |
+1 |
–1 |
–1 |
+1 |
y11 |
y12 |
… |
y1l |
… |
y1m |
|
|
||
|
2 |
k21 |
k22 |
… |
k2l |
… |
k2m |
+1 |
+1 |
–1 |
–1 |
y21 |
y22 |
… |
y2l |
… |
y2m |
|
|
||
|
3 |
k31 |
k32 |
… |
k3l |
… |
k3m |
+1 |
–1 |
+1 |
–1 |
y31 |
y32 |
… |
y3l |
… |
y3m |
|
|
||
|
4 |
k41 |
k42 |
… |
k4l |
… |
k4m |
+1 |
+1 |
+1 |
+1 |
y41 |
y42 |
… |
y4l |
… |
y4m |
|
|
||
Почему рандомизация опытов важна, мы попытаемся показать на следующем примере.
Рассмотрим матрицу 23, полученную из матрицы 22 обычным способом: два раза повторен план 22, причем в первых четырех опытах x3 имеет верхнее значение, а в последних четырех опытах – нижнее значение. Допустим, что экспериментатор может поставить в первый день четыре опыта и во второй день также четыре опыта.
Можно ли опыты ставить подряд и в первый день реализовать опыты № 1, 2, 3 и 4, а во второй – 5, 6, 7 и 8? Ставя опыты подряд, вы разбиваете матрицу на две части или на два блока: в первый блок – входят опыты № 1, 2, 3 и 4, во второй – № 5, 6, 7 и 8. Если внешние условия первого дня каким-то образом отличались от внешних условий второго дня, то это способствовало возникновению некоторой систематической ошибки. Обозначим эту ошибку ε. Тогда четыре значения параметра оптимизации сдвинуты на величину ε по сравнению с истинными значениями. Пусть это будут параметры, входящие в первый блок: y1+ε, y2+ε, y3+ε, y4+ε. Однако матрица построена так, что в первом блоке значения х3 находятся на верхнем уровне, а во втором – на нижнем уровне. Тогда при подсчете b3 получится следующая картина:
b3= [(y1+ε)+(y2+ε)+(y3+ε)+(y4+ε)–y5–y6–y7–y8]→β3+
[(y1+ε)+(y2+ε)+(y3+ε)+(y4+ε)–y5–y6–y7–y8]→β3+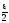 .
.
где β3 – истинное значение коэффициента при х3. Таким образом, возможное различие во внешних условиях смешалось с величиной линейного коэффициента b3 и исказило это значение. В такой последовательности опыты ставить нельзя. Опыты нужно рандомизировать во времени, т.е. придать последовательности опытов случайный характер.
Приведем простой пример рандомизации условий эксперимента. В полном факторном эксперименте 23 предполагается каждое значение параметра оптимизации определять по двум параллельным опытам. Нужно случайно расположить всего 16 опытов. Присвоим параллельным опытам номера с 9 по 16, и тогда опыт № 9 будет повторным по отношению к первому опыту, десятый – ко второму и т. д. Следующий этап рандомизации – использование таблицы случайных чисел. Обычно таблица случайных чисел приводится в руководствах по математической статистике. В случайном месте таблицы выписываются числа с 1 по 16 с отбрасыванием чисел больше 16 и уже выписанных. В нашем случае, начиная с четвертого столбца, можно получить такую последовательность:
2; 15; 9; 5; 12; 14; 8; 13; 16; 1; 3; 7; 4; 6; 11; 10.
Это значит, что первым реализуется опыт № 2, вторым – опыт № 7 и т.д. Выбранную случайным образом последовательность опытов не рекомендуется нарушать.
Если экспериментатор располагает сведениями о предстоящих изменениях внешней среды, сырья, аппаратуры и т. п., то целесообразно планировать эксперимент таким образом, чтобы эффект влияния внешних условий был смешан с определенным взаимодействием, которое не жалко потерять. Так, при наличии двух партий сырья матрицу 23 можно разбить на два блока таким образом, чтобы эффект сырья сказался на величине трехфакторного взаимодействия. Тогда все линейные коэффициенты и парные взаимодействия будут освобождены от влияния неоднородности сырья (табл.).
В этой матрице при составлении блока 1 отобраны все строки, для которых х1х2х3=+1, а при составлении блока 2 – все строки, для которых х1х2х3=–1. Различие в сырье можно рассматривать как новый фактор x4. Тогда матрица 23, разбитая на два блока, представляет собой полуреплику 24–1 с определяющим контрастом 1=х1х2х3x4.
|
№ |
x0 |
x1 |
х2 |
х3 |
х1х2 |
х1х3 |
х2х3 |
х1х2х3 |
y |
|
1 |
+ |
– |
– |
+ |
+ |
– |
– |
+ |
y1+ε |
|
+ |
+ |
– |
– |
– |
– |
+ |
+ |
y2+ε |
|
|
+ |
– |
+ |
– |
– |
+ |
– |
+ |
y3+ε |
|
|
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
y4+ε |
|
|
2 |
+ |
– |
– |
– |
+ |
+ |
+ |
– |
y5 |
|
+ |
+ |
– |
+ |
– |
+ |
– |
– |
y6 |
|
|
+ |
– |
+ |
+ |
– |
– |
+ |
– |
y7 |
|
|
+ |
+ |
+ |
– |
+ |
– |
– |
– |
y8 |
Эффект сырья отразился на подсчете свободного члена b0 и эффекта взаимодействия второго порядка b123. Аналогично можно разбить на два блока любой эксперимент типа 2k. Главное – правильно выбрать взаимодействие, которым можно безболезненно пожертвовать. При отсутствии априорных сведений выбирают взаимодействие самого высокого порядка.
При необходимости разбиения матрицы на большее количество блоков применяют блочное планирование, например планирование по типу латинского квадрата и пр.
Результаты эксперимента для каждой строки опытов записываются в столбцы yim таблицы и производится их осреднение
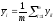 .
.
То есть, среднее арифметическое у равно сумме всех m отдельных результатов, деленной на количество параллельных опытов m
Отклонение
результата любого опыта от среднего
арифметического можно представить как
разность yq
–
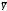 ,
где yq
– результат отдельного опыта. Наличие
отклонения свидетельствует об
изменчивости, вариации значений повторных
опытов. Для измерения этой изменчивости
чаще всего используют дисперсию.
,
где yq
– результат отдельного опыта. Наличие
отклонения свидетельствует об
изменчивости, вариации значений повторных
опытов. Для измерения этой изменчивости
чаще всего используют дисперсию.
Дисперсией называется среднее значение квадрата отклонений величины от ее среднего значения. Дисперсия обозначается s2 и выражается формулой
 .
.
где (m–1) – число степеней свободы, равное количеству опытов минус единица. Одна степень свободы использована для вычисления среднего.
Корень квадратный из дисперсии, взятый с положительным знаком, называется средним квадратическим отклонением, стандартом или квадратичной ошибкойю
Дисперсия и с.к.о. – это меры рассеяния, изменчивости. Чем больше дисперсия и стандарт, тем больше рассеяны значения параллельных опытов около среднего значения.
Ошибка опыта является суммарной величиной, результатом многих ошибок: ошибок измерений факторов, ошибок измерений параметра оптимизации и др. Каждую из этих ошибок можно, в свою очередь, разделить на составляющие.
Все ошибки принято разделять на два класса: систематические и случайные. Систематические ошибки порождаются причинами, действующими регулярно, в определенном направлении. Чаще всего эти ошибки можно изучить и определить количественно. Систематические ошибки находят, калибруя измерительные приборы и сопоставляя опытные данные с изменяющимися внешними условиями. Если систематические ошибки вызываются внешними условиями (переменной температуры, сырья и т.д.), следует компенсировать их влияние с помощью рандомизации. Случайными ошибками называются те, которые появляются нерегулярно, причины возникновения которых неизвестны и которые невозможно учесть заранее.
Систематические и случайные ошибки состоят из множества элементарных ошибок. Для того чтобы исключать инструментальные ошибки, следует проверять приборы перед опытом, иногда в течение опыта и обязательно после опыта.
Очень важно исключить из экспериментальных данных грубые ошибки, так называемый брак при повторных опытах. Ни в коем случае, конечно, нельзя вносить поправки самовольно, Для отброса ошибочных опытов .существуют правила (критерий Стьюдента, трехсигмовый критерий и др.).
Мы нашли, как подсчитывается дисперсия в каждом опыте, т.е. в каждой горизонтальной строке матрицы планирования.
Матрица планирования состоит из серии опытов, и дисперсия всего эксперимента получается в результате усреднения дисперсий всех опытов. По терминологии, принятой в планировании эксперимента, речь идет о подсчете дисперсии параметра оптимизации или, что то же самое, дисперсии воспроизводимости эксперимента (или дисперсии ошибки эксперимента).
 ,
или
,
или

Дисперсию воспроизводимости проще всего рассчитывать, когда соблюдается равенство числа повторных опытов во всех экспериментальных точках. На практике часто приходится сталкиваться со случаями, когда число повторных опытов различно. Это происходит вследствие отброса грубых наблюдений, неуверенности экспериментатора в правильности некоторых результатов (в таких случаях возникает желание еще и еще раз повторить опыт) и т.п.
Тогда при усреднении дисперсий приходится пользоваться средним взвешенным значением дисперсий, взятым с учетом числа степеней свободы. Число степеней свободы средней дисперсии в таком случае принимается равным сумме чисел степеней свободы дисперсий, из которых она вычислена.
Формулами для расчета дисперсии воспроизводимости можно пользоваться только в том случае, если дисперсии однородны. Последнее означает, что среди всех суммируемых дисперсий нет таких, которые бы значительно превышали все остальные.
Одним из требований регрессионного анализа является однородность дисперсий.
Проверка однородности дисперсий производится с помощью различных статистических критериев. Простейшим из них является критерий Фишера, предназначенный для сравнения двух дисперсий. Критерий Фишера (F-критерий) представляет собою отношение большей дисперсии к меньшей. Полученная величина сравнивается с табличной величиной F-критерия.
Если сравниваемое количество дисперсий больше двух и одна дисперсия значительно превышает остальные, можно воспользоваться критерием Кохрена. Этот критерий пригоден для случаев, когда во всех точках имеется одинаковое число повторных опытов.
В
терминах дисперсионного анализа задача
заключается в проверке нулевой гипотезы
о равенстве дисперсий
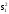 =
=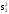 =
=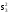 =
= =
=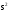 во всех вариантах эксперимента.
во всех вариантах эксперимента.
Критерий Кохрена – это отношение максимальной дисперсии к сумме всех дисперсий
 .
.
С этим критерием связаны числа степеней свободы f1=m–1 и f2=N.
Гипотеза об однородности дисперсий подтверждается, если вычисленное значение G окажется меньше значения Gкрит, найденного по таблице для выбранного уровня значимости α. Тогда говорят, что данные эксперимента не противоречат проверяемой гипотезе об однородности дисперсий. Тогда можно усреднять дисперсии и пользоваться формулой для определения дисперсии воспроизводимости

с N(m–1) степенями свободы.
Если проверка воспроизводимости дала отрицательный результат, то остается признать невоспроизводимость эксперимента вследствие наличия в объекте источников неоднородности, для выделения которых следует обратиться к приемам дисперсионного анализа.
После проверки воспроизводимости эксперимента можно перейти к определению модели эксперимента в виде уравнений регрессии.
Статистики разработали много разнообразных методов обработки результатов эксперимента. Но, пожалуй, ни один из них не может конкурировать по популярности, по широте приложений с методом наименьших квадратов (МНК), который был развит усилиями Лежандра и Гаусса более 150 лет назад.
Давайте попробуем разобраться в этом методе. Начнем с протого случая: один фактор, линейная модель. Интересующая нас функция отклика (которую мы будем также называть уравнением регрессии) имеет вид
y=b0+b1x1.
Это хорошо известное вам уравнение прямой линии. Наша цель – вычисление неизвестных коэффициентов b0 и b1. Мы провели эксперимент, чтобы использовать при вычислениях его результаты.
Если бы все экспериментальные точки лежали строго на прямой линии, то для каждой из них было бы справедливо равенство
yi–b0–b1x1i=0,
где i=1, 2, . . . , N – номер опыта. Тогда не было бы никакой проблемы. На практике это равенство нарушается и вместо него приходится писать
yi–b0–b1x1i=εi.
где εi – разность между экспериментальным и вычисленным по уравнению регрессии значениями у в i-й экспериментальной точке. Эту величину иногда называют невязкой.
Действительно, невязка возникает по двум причинам: из-за ошибки эксперимента и из-за непригодности модели. Причем эти причины смешаны и мы не можем, не получив дополнительной информации, сказать, какая из них преобладает. Можно постулировать, что модель пригодна. Тогда невязка будет порождаться только ошибкой опыта. (Еще можно, конечно, постулировать, что ошибка опыта равна нулю. Тогда невязка будет связана только с пригодностью модели, и пригодной будет такая модель, для которой все невязки равны нулю.)
Конечно, мы хотим найти такие коэффициенты регрессии, при которых невязки будут минимальны. Это требование можно записать по-разному. В зависимости от этого мы будем получать разные оценки коэффициентов. Вот одна из возможных записей
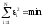 ,
,
которая приводит к методу наименьших квадратов.
Когда мы ставим эксперимент, то обычно стремимся провести больше (во всяком случае не меньше) опытов, чем число неизвестных коэффициентов. Поэтому система линейных уравнений оказывается переопределенной и часто противоречивой (т.е. она может иметь бесконечно много решений или может не иметь решений). Переопределенность возникает, когда число уравнений больше числа неизвестных; противоречивость – когда некоторые из уравнений несовместимы друг с другом.
Только если все экспериментальные точки лежат на прямой, система становится определенной и имеет единственное решение.
МНК обладает тем замечательным свойством, что он делает определенной любую произвольную систему уравнений. Он делает число уравнений равным числу неизвестных коэффициентов.
Наше уравнение регрессии имеет вид y=b0+b1x1.
В нем два неизвестных коэффициента. Значит, применяя МНК, мы получим два уравнения.
Давайте
попробуем их получить. Мы записали
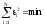 .
.
Это
соотношение можно записать иначе
 .
.
Вы, конечно, помните из курса математики, что минимум некоторой функции, если он существует, достигается при одновременном равенстве нулю частных производных по всем неизвестным.
Вот откуда берутся наши уравнения для определения коэффициентов.
Проверка значимости каждого коэффициента проводится независимо.
Ее можно осуществлять двумя равноценными способами: проверкой по t-критерию Стьюдента или построением доверительного интервала. При использовании полного факторного эксперимента или регулярных дробных реплик доверительные интервалы для всех коэффициентов (в том числе и эффектов взаимодействия) равны друг другу.
Прежде
всего надо, конечно, найти дисперсию
коэффициента регрессии s2{bj}.
Она определяется в нашем случае по
формуле
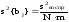
По сути при проверке значимости оценок коэффициентов уравнения регрессии требуется проверить нулевую гипотезу H0: βj=0 относительно конкурирующей H1: βj≠0. Проверка гипотезы проводится с помощью t–статистики Стьюдента, которая вычисляется по формуле:
 ,
,
где s{bj} – среднеквадратичное отклонение оценки коэффициентов bj.
Если найденная величина tj превышает критическое значение, определяемое по таблице для числа степеней свободы f=N(m–1) и заданной значимости α, то нулевая гипотеза H0 отвергается и коэффициент bj считается значимым. В противном случае (при tj≤tкрит) нуль–гипотеза принимается и коэффициент bj считают статистически незначимым.
Незначимость некоторого коэффициента показывает, что в выбранном диапазоне варьирования переменных xj отсутствует статистически значимое влияние данного фактора на выходную переменную y. Поскольку вычисленные оценки коэффициентов являются независимыми, то фактор с незначимым коэффициентом может быть выброшен из уравнения регрессии без пересчета остальных значимых коэффициентов.
После исключения факторов с незначимыми коэффициентами производится проверка адекватности полученной модели.
Для характеристики среднего разброса относительно линии регрессии вполне подходит остаточная сумма квадратов. Неудобство состоит в том, что она зависит от числа коэффициентов в уравнении: введите столько коэффициентов, сколько вы провели независимых опытов, и получите остаточную сумму, равную нулю.
Числом степеней свободы в статистике называется разность между числом опытов и числом коэффициентов (констант), которые вычислены по результатам этих опытов независимо друг от друга.
Если, например, вы провели полный факторный эксперимент 23 и нашли линейное уравнение регрессии, то число степеней свободы f=N–(k+1)=8–(3+1)=4.
Остаточная
сумма квадратов, деленная на число
степеней свободы, называется остаточной
дисперсией
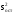 ,
или дисперсией адекватности и характеризует
рассеяние результатов эксперимента
относительно подобранного уравнения
регрессии. Дисперсия адекватности
находится следующим образом:
,
или дисперсией адекватности и характеризует
рассеяние результатов эксперимента
относительно подобранного уравнения
регрессии. Дисперсия адекватности
находится следующим образом:
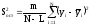
где т – число параллельных опытов; L – число оцениваемых коэффициентов в уравнении регрессии. Остаточная дисперсия оценивается с числом степеней свободы f=N–L.
Рассмотрим
пример. Требуется найти число степеней
свободы для
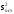 в следующем случае: план 23–1
и четыре параллельных опыта в нулевой
точке для вычисления ошибки опыта;
модель линейная.
в следующем случае: план 23–1
и четыре параллельных опыта в нулевой
точке для вычисления ошибки опыта;
модель линейная.
Один из возможных ответов – семь степеней свободы – осован на следующих предположениях. Вероятно, вы рассуждали так. Проделано 12 опытов: 24–1=8 плюс 4 нулевых. В уравнение входит 5 коэффициентов. Следовательно, f=12–5=7. Здесь не учтено, что параллельные опыты нельзя считать самостоятельными, так как они дублируют друг друга. Поэтому они все дают одну степень свободы. Другой неправильный ответ – 4 степени свободы. Этот неправильный ответ получился, вероятно, из следующего рассуждения. Проделано 12 опытов: восемь по матрице планирования и четыре нулевых. Так как все нулевые опыты тождественны, то они дают одну степень свободы. Число коэффициентов в модели равно пяти. Следовательно, f=9–5=4. Вы не обратили внимание на то, что опыты в нулевой точке не используются при вычислении коэффициентов и- не могут поэтому входить в число степеней свободы.
Правильный ответ – три степени свободы. Действительно, мы провели 12 опытов, но четыре опыта в нулевой точке были проведены для других целей и в вычислении коэффициентов не участвовали, поэтому они не входят в число степеней свободы. (А если бы входили – такие случаи возможны, то давали бы не четыре, а только одну степень свободы.) Число коэффициентов модели – пять. Следовательно, f = 8 – 5 = 3.
Запомните правило: в планировании эксперимента число степеней свободы для дисперсии адекватности равно числу различных опытов, результаты которых используются при подсчете коэффициентов регрессии, минус число определяемых коэффициентов.
Для проверки гипотезы об адекватности можно использовать F-критерий (Фишера).
Тогда для проверки адекватности выясняется соотношение между остаточной дисперсией и дисперсией ошибки эксперимента.
Если
остаточная дисперсия (или дисперсия
адекватности) не превышает ошибки
эксперимента, то считается, что модель
адекватно представляет результаты
эксперимента: если остаточная дисперсия
больше дисперсии ошибки эксперимента,
то модель нельзя признать пригодной.
Следовательно, проверяется нулевая
гипотеза Н0:
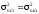 против Н1:
против Н1:
 с помощью F–отношения:
F=
с помощью F–отношения:
F=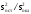 .
Если вычисленное отношение меньше
Fкрит,
найденного по таблице для соответствующих
степеней свободы числителя fост=N–L,
знаменателя fош=N(m–1)
и выбранной вероятности 1–α, то
нуль–гипотеза принимается. В противном
случае гипотеза отвергается и модель
признается не пригодной для представления
выборочных данных эксперимента.
.
Если вычисленное отношение меньше
Fкрит,
найденного по таблице для соответствующих
степеней свободы числителя fост=N–L,
знаменателя fош=N(m–1)
и выбранной вероятности 1–α, то
нуль–гипотеза принимается. В противном
случае гипотеза отвергается и модель
признается не пригодной для представления
выборочных данных эксперимента.
Таблица критерия Фишера построена следующим образом. Столбцы связаны с определенным числом степеней свободы для числителя f1, а строки – для знаменателя f2. На пересечении соответствующих строки и столбца стоят критические значения F-критерия. Как правило, в технических задачах используется уровень значимости 0,05.
Лекция 5.
Оценки истинного значения измеряемой величины.
Типы оценок и их свойства. Точечные оценки. Доверительные оценки при равноточных измерениях. Доверительные оценки при неравноточных измерениях. Необходимое количество измерений.
Оценка. Целью статистической оценки является отыскание оценки параметра генеральной совокупности на основе выборочной статистики, взятой из этой совокупности. Обычно требуются два типа оценок: точечные оценки и интервальные оценки.
Точечная оценка — это численное значение статистики, используемое для оценки параметра распределения генеральной совокупности. Например, выборочное среднее x — точечная оценка математического ожидания генеральной совокупности μ. Обычно предполагается, что точечные оценки имеют определенные свойства.
Оценки должны удовлетворять следующим требованиям:
- оценка должна быть состоятельной, т. е. с увеличением объема выборки она должна сходиться к оцениваемому параметру по вероятности;
- оценка должна быть эффективной, т. е. при данном объеме выборки иметь минимальную дисперсию.
- оценка должна быть несмещенной, т. е. математическое ожидание оценки должно равняться оцениваемому параметру.
Общий метод нахождения оценок с нужными свойствами это метод максимума правдоподобия. Практическое значение имеют следующие выборочные характеристики, которые удовлетворяют вышеперечисленным требованиям:
1) в качестве оценки математического ожидания – среднее арифметическое выборки:
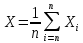 ,
(1)
,
(1)
2) в качестве оценки дисперсии случайной величины х - значение, определяемое формулой:
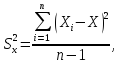 (2)
(2)
3) в качестве оценки дисперсии среднего арифметического x - значение, определяемое формулой:
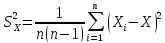 ,
(3)
,
(3)
Точечные оценки. Если все n измерений величины а произведены с одинаковой точностью (равноточные измерения), то в качестве оценки истинного значения а измеряемой величины применяют среднее арифметическое значение результатов измерений:
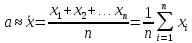 ,
(4)
,
(4)
Эта оценка является несмещенной и состоятельной. При дополнительном предположении, что случайные ошибки измерения подчинены нормальному закону распределения вероятностей, эта оценка является эффективной.
Если измерения не являются равноточными, но известны веса измерений, т.е. числа p1, p2, ….pn, обратно пропорциональные дисперсиям ошибок σ1, σ2 …. σn:
p1
:
p2
:
…:pn
=
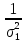 :
:
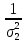 :……
:……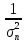
то в качестве оценки истинного значения a измеряемой величины применяют взвешенное среднее арифметическое значение:
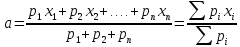 ,
(5)
,
(5)
Эта оценка обладает теми же свойствами, что и оценка (4). Полезно обратить внимание на то, что взвешенное среднее арифметическое значение (5) зависит не от самих весов p1 p2 ..рп, а только от их отношений.
Например, часто обрабатываемые результаты xl x2, хп представляют собой не результаты непосредственных измерений, а средние в п сериях измерений, произведенных с одной и той же точностью (т. е. с одинаковой средней квадратической ошибкой σ), но при разных количествах измерений в каждой серии. В этом случае каждому значению хi можно приписать в качестве веса количество измерений в соответствующей серии:
pi = mi (i=1, 2, п),
где
тi
— количество измерений в серии со
средним значением xi.
Это связано с тем, что при указанных
условиях дисперсий
 средних значений
xt
обратно пропорциональны количествам
измерений
тi
в соответствующих сериях:
средних значений
xt
обратно пропорциональны количествам
измерений
тi
в соответствующих сериях:
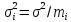
и, значит,
 :
:
 :……
:……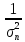 = m1:
m2
: ....mn
= m1:
m2
: ....mn
Среднее арифметическое значение для интервального ряда данных является смещенной оценкой для а. Величина смещения имеет порядок h2, если длина интервала h достаточно мала (в 2—3 раза меньше, чем σ).
Доверительные оценки при равноточных: измерениях. Приводимые ниже доверительные оценки истинного значения а измеряемой величины даются в предположении, что случайные ошибки измерения подчинены нормальному закону распределения вероятностей, Здесь рассматриваются только симметричные доверительные оценки, которые имеют вид неравенств
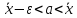
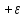
или
|а
-
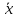 | <
ε
(6)
| <
ε
(6)
где
 -
среднее арифметическое значение (4).
-
среднее арифметическое значение (4).
Величина
ε определяется по заданной доверительной
вероятности (надежности оценки)
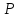 ;
обычно надежность
;
обычно надежность
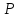 задается в виде
одного из трех уровней 0,95, 0,99 или 0,999.
задается в виде
одного из трех уровней 0,95, 0,99 или 0,999.
Доверительная оценка при известной точности измерений.
Если заранее известна средняя квадратическая ошибка а (или другая связанная с ней характеристика точности измерений), то доверительная оценка (6) имеет вид
|а—х|
<
t(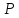 )σ/
)σ/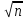 , (7)
, (7)
где
п —
число измерений, а значение
t
= t(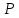 )
определяется по заданной доверительной
вероятности <
)
определяется по заданной доверительной
вероятности <
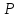 из условия
из условия
2Ф
(t)
=
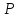 (8)
(8)
т. е. находится по (прилож. стр. 172).
Таким образом, здесь
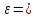 t
(
t
(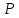 )
)
Пример
1.
Пусть для десяти измерений, результаты
которых приведены в примере (предыдущей
лекции), известно, что σ = 0,28; требуется
оценить истинное значение измеряемой
величины а
с надежностью
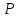 = 0,99.
= 0,99.
Решение.
По (прилож. С. 172) для
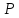 = 2Ф (t)
= 0,99, т. е. для 1 -
= 2Ф (t)
= 0,99, т. е. для 1 -
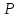 = 0,01, находим t
= 2,576. Подсчитанное среднее значение
результатов измерения равно
= 0,01, находим t
= 2,576. Подсчитанное среднее значение
результатов измерения равно
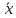 =
36,06. Следовательно, с надежностью 0,99
можно считать, что
=
36,06. Следовательно, с надежностью 0,99
можно считать, что
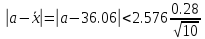 =
0.23
=
0.23
т. е. что значение а лежит в интервале (35,83; 36,29)
Доверительная оценка при неизвестной точности измерений. Если средняя квадратическаи ошибка σ заранее неизвестна, то вместо нее используют эмпирический стандарт
![]()
который служит оценкой параметра σ. При этом доверительная оценка (6) принимает вид
|а
-
 |
<
t(
|
<
t( )
)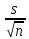 (9)
(9)
где
множитель
t
( )
зависит уже не только от доверительной
вероятности
)
зависит уже не только от доверительной
вероятности
 ,
но и от числа измерений n
(k
= n
- 1). Значения этого множителя для пяти
уровней надежности
,
но и от числа измерений n
(k
= n
- 1). Значения этого множителя для пяти
уровней надежности
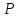 и для различных значений числа приведены
в (прилож, стр. 174). Таблица составлена
с помощью так называемого
распределения Стьюдента,
т. е. распределения вероятностей отношения
и для различных значений числа приведены
в (прилож, стр. 174). Таблица составлена
с помощью так называемого
распределения Стьюдента,
т. е. распределения вероятностей отношения
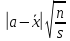 :
значения
t
= t(
:
значения
t
= t( )
определены так, что
)
определены так, что
![]()
Распределение Стьюдента зависит от одного параметра k, который называется числом степеней свободы; для рассматриваемой задачи число степеней свободы k связано с числом измерений п соотношением k = n - 1.
Пример
2. Пусть для десяти измерений, результаты
которых приведены в примере (тот же
самый), величина σ не известна. Требуется
оценить истинное значение измеряемой
величины а
с надежностью
 = 0,99.
= 0,99.
Решение.
Для результатов измерений среднее
значение и среднее квадратическое
отклонение подсчитаны и составляют
соответственно
х = 36,06
и s*
= 0,25. По заданной надежности
 = 0,99
и числу измерений n
= 10 находим по табл. IV множитель t
(0,99; 9) = 3,250 и получаем доверительную
оценку истинного значения а
в виде
= 0,99
и числу измерений n
= 10 находим по табл. IV множитель t
(0,99; 9) = 3,250 и получаем доверительную
оценку истинного значения а
в виде
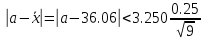 =
0,27
=
0,27
таким образом, с надежностью 0,99 можно считать, что значение а заключено в интервале (З5,79; 36,33).
Правило трех сигм. Так как выбор надежности доверительной опенки допускает некоторый произвол, в практике обработки результатов эксперимента широкое распространение получило правило трех сигм;
Отклонение истинного значения измеряемой величины от среднего арифметического значения результатов измерений не превосходит, утроенной средней квадратической ошибки этого среднего значения.
Таким образом, правило трех сигм представляет собой доверительную оценку
|а—х
| < 3σ/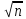
в
случае известной величины σ или
доверительную оценку |а—х|
<
3s/ в
случае неизвестной величины σ.
в
случае неизвестной величины σ.
Необходимое
количество измерений. Увеличивая
количество измерений n
даже при неизменной их точности, можно
увеличить надежность доверительных
оценок (7) и (9) или сузить доверительный
интервал для истинного значения
измеряемой величины. Необходимое
количество измерений для достижения
требуемой точности е и требуемой
надежности
 можно определить заранее только в том
случае, когда известна средняя
квадратическая ошибка измерений
(измерения предполагаются равноточными
и независимыми). В этом случае количество
измерений для получения доверительной
оценки точности ε:
можно определить заранее только в том
случае, когда известна средняя
квадратическая ошибка измерений
(измерения предполагаются равноточными
и независимыми). В этом случае количество
измерений для получения доверительной
оценки точности ε:
|а
-
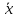 |
< ε, с
заданной надежностью
|
< ε, с
заданной надежностью
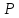 определяется с помощью формулы (7),
откуда
определяется с помощью формулы (7),
откуда
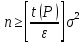
где
t
= t
( )
находится из равенства 2Ф(t)*=
)
находится из равенства 2Ф(t)*=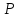 по (прилож/, стр. 172)/
по (прилож/, стр. 172)/
Если
средняя квадратическая ошибка измерений
заранее неизвестна, но известен хотя
бы ее порядок, то необходимое количество
измерений можно определить в зависимости
от надежности
(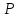 )
и
от отношения
q
=
ε/s,
где s
будущий эмпирический стандарт ошибки.
Для определения количества
п
в зависимости
от
t
(
)
и
от отношения
q
=
ε/s,
где s
будущий эмпирический стандарт ошибки.
Для определения количества
п
в зависимости
от
t
(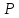 )
и
q
применяется табл. 2.
)
и
q
применяется табл. 2.
Таблица 2
|
( |
0,90 |
0,95 |
0,98 |
0,99 |
0,999 |
|
1,0 |
5 |
7 |
9 |
11 |
17 |
|
0,5 |
13 |
18 |
25 |
31 |
50 |
|
0,4 |
19 |
27 |
37 |
46 |
74 |
|
0,3 |
32 |
46 |
64 |
78 |
127 |
|
0,2 |
70 |
99 |
139 |
171 |
277 |
|
0,1 |
273 |
387 |
545 |
668 |
1089 |
|
0,05 |
1084 |
1540 |
2168 |
2659 |
4338 |
Например,
чтобы гарантировать получение
доверительной оценки с надежностью
 = 0,99 и точностью до 0,1s,
надо произвести 688 измерений. На практике
часто можно ограничиться меньшим числом
измерений, если применить следующий
прием. Сначала нужно произвести
Сравнительно небольшое количество
измерений (в 3
- 4 раза меньше
указанного в таблице). По результатам
этих измерений рассчитать доверительный
интервал. Затем уточнить необходимое
количество измерений из тех соображений,
что уменьшение доверительного интервала
в
= 0,99 и точностью до 0,1s,
надо произвести 688 измерений. На практике
часто можно ограничиться меньшим числом
измерений, если применить следующий
прием. Сначала нужно произвести
Сравнительно небольшое количество
измерений (в 3
- 4 раза меньше
указанного в таблице). По результатам
этих измерений рассчитать доверительный
интервал. Затем уточнить необходимое
количество измерений из тех соображений,
что уменьшение доверительного интервала
в
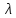 раз обеспечивается увеличением количества
измерений в
раз обеспечивается увеличением количества
измерений в
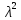 раз (например, уменьшение доверительного
интервала в 2 раза обеспечивается
увеличением количества измерений в
4
раза).
раз (например, уменьшение доверительного
интервала в 2 раза обеспечивается
увеличением количества измерений в
4
раза).
Пример. Приведенная доверительная оценка истинного значения а некоторой величины по результатам n = 10 ее измерений дала точность 0,27 с надежностью 0,99. Если при той же надежности мы хотим оценить а с точностью до 0,1, т. е. уменьшить доверительный интервал в 2,7 раза, то мы должны довести число измерений до 10 (2,7)2 = 73 (на самом деле немного меньше, так как при этом и t (0,99; k) уменьшится с 3,25 до 2,65).
Заметим, что больший эффект дает увеличение точности отдельных измерений
Лекция 6.
Сравнение средних значений.
Сравнение средних при известных дисперсиях. Сравнение средних при неизвестной дисперсии. Проверка гипотезы о равенстве средних значений.
Целью эксперимента нередко бывает выявление различий между значениями определенного параметра в разных объектах исследования. Например, при создания нового материала (или прибора) может быть обнаружено, что значение какого-либо его параметра отличается от значений того же параметра у ранее созданного материала (или прибора), но отличие незначительно; при этом возникает подозрение, не вызвано ли это отличие лишь
случайными ошибками эксперимента. Аналогичный вопрос возникает в промышленности, когда в разных условиях (например, на разном оборудовании или при разной технологии) изготовляются изделия с одними и теми же заданными номинальными значениями какого-либо параметра, а проверка обнаруживает расхождение между средними значениями этих параметров; здесь важно выяснить, имеем ли мы дело с различным качеством изделий или со случайными отклонениями.
Для
выяснения вопроса о случайном или
неслучайном расхождении значений
некоторого параметра х проводят две
серии экспериментов (измерений) и для
каждой из них подсчитывают среднее
значение параметра, скажем,
 и
и
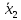 .
Вопрос сводится к тому, когда считать
разность между этими средними достаточно
большой для того, чтобы иметь практическую
уверенность в неслучайном происхождении
обнаруженных различий.
.
Вопрос сводится к тому, когда считать
разность между этими средними достаточно
большой для того, чтобы иметь практическую
уверенность в неслучайном происхождении
обнаруженных различий.
Ниже излагается решение этого вопроса в терминах результатов измерений. Измерения предполагаются независимыми и, по крайней мере, в пределах каждой серии, равноточными; распределение ошибок измерения предполагается нормальным.
Сравнение
средних при известных дисперсиях.
Пусть произведено n1,
независимых равноточных измерений в
первой серии и
п2
- во второй, причем заранее известны
дисперсии ошибок в первой и во второй
сериях (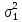 и
и
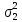 |
соответственно). Средние значения
результатов измерений в первой и во
второй сериях обозначим соответственно
через
|
соответственно). Средние значения
результатов измерений в первой и во
второй сериях обозначим соответственно
через
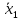 и
и
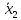 .
Для решения вопроса о случайном или
неслучайном расхождении этих средних
значений подсчитываем отношение
.
Для решения вопроса о случайном или
неслучайном расхождении этих средних
значений подсчитываем отношение
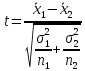 ,
(1)
,
(1)
Далее
задаем желаемую вероятность вывода
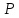 и по ней находим (прилож, стр. 172)
соответствующее значение
t
(
и по ней находим (прилож, стр. 172)
соответствующее значение
t
(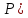 (например,
при
(например,
при
 = 0,99 находим
t
= 2,576).
= 0,99 находим
t
= 2,576).
Если
абсолютная величина отношения (1)
превосходит найденное значение
t
(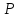 ),
то расхождение средних значений можно
считать неслучайным
(значимым) с
надежностью вывода
),
то расхождение средних значений можно
считать неслучайным
(значимым) с
надежностью вывода
 .
В противном случае нет оснований считать
расхождение значимым (т. е. оно может
быть объяснено случайными отклонениями).
.
В противном случае нет оснований считать
расхождение значимым (т. е. оно может
быть объяснено случайными отклонениями).
На
практике иногда поступают следующим
образом. Подсчитав отношение (1), находят
по табл. ближайшее к нему
меньшее
значение
t
(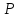 ).
Тогда вывод о значимости расхождения
средних значений имеет надежность
).
Тогда вывод о значимости расхождения
средних значений имеет надежность
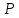 .
Если эта надежность достаточна, то
указанный вывод принимается, в противном
случае — отбрасывается. Если надежность
вывода недостаточна, а сомнение в
неслучайности расхождения средних
осталось, то может оказаться целесообразным
увеличить число измерений в каждой
серии для более надежного решения
вопроса.
.
Если эта надежность достаточна, то
указанный вывод принимается, в противном
случае — отбрасывается. Если надежность
вывода недостаточна, а сомнение в
неслучайности расхождения средних
осталось, то может оказаться целесообразным
увеличить число измерений в каждой
серии для более надежного решения
вопроса.
Если
дисперсии ошибок для обеих серий
измерений одинаковы:

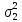 =
σ2, то отношение (1) сводится к
=
σ2, то отношение (1) сводится к
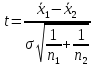 ,
(2)
,
(2)
Сравнение
средних при неизвестной дисперсии.
Если дисперсии ошибок заранее не
известны, то сравнение средних производится
только при добавочном предположении,
что
дисперсии ошибок в обеих сериях измерений
одинаковы (это
предположение либо принимается без
проверки, например, когда две серии
измерений производятся одним и тем же
прибором, Пусть с одной и той же точностью
произведены две серии независимых
измерений, причем
п1
измерений в первой серии дали среднее
значение
 и эмпирическую
где
и эмпирическую
где
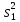 и
п2
измерений во второй серии дали
соответственно
и
п2
измерений во второй серии дали
соответственно
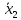 и
и
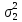 .
Для решения вопроса о случайном или
неслучайном расхождении средних значений
подсчитываем отношение
.
Для решения вопроса о случайном или
неслучайном расхождении средних значений
подсчитываем отношение
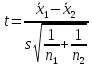 ,
(3)
,
(3)
где
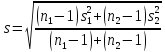 ,
(4)
,
(4)
Далее
задаем желаемую вероятность вывода
 и в (приложение, стр. 174) находим значение
t
(
и в (приложение, стр. 174) находим значение
t
(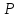 k),
соответствующее заданной вероятности
k),
соответствующее заданной вероятности
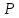 и числу степеней свободы
k
= n1
+ n2
- 2.
и числу степеней свободы
k
= n1
+ n2
- 2.
Если
абсолютная величина отношения (3)
превосходит найденное значение
t
(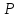 ;
k),
то расхождение средних значений можно
считать неслучайным (значимым) с
надежностью вывода
;
k),
то расхождение средних значений можно
считать неслучайным (значимым) с
надежностью вывода
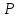 .
В противном случае нет оснований считать
расхождение значимым.
.
В противном случае нет оснований считать
расхождение значимым.
Заметим,
что если отношение (3) оказывается лишь
немного меньшим значения
t
(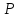 ;
k)
при заданной вероятности
;
k)
при заданной вероятности
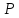 ,
то может быть целесообразным увеличить
число измерений для получения более
надежного вывода (тем более, что значения
t
(
,
то может быть целесообразным увеличить
число измерений для получения более
надежного вывода (тем более, что значения
t
(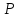 k)
уменьшаются с увеличением k).
k)
уменьшаются с увеличением k).
Величина определяемая по формуле, (4), служит оценкой неизвестной дисперсии s2 . Ее можно представить также через средние квадратические отклонения от средних значений
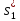 =
=
 ,
,
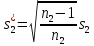
А именно
 ,
(5)
,
(5)
Проверка
гипотезы о равенстве средних значений.
Методы сравнения средних значений можно
применять и для решения задачи проверки
гипотезы о равенстве средних. Задача
эта ставится следующим образом. Имеются
две совокупности элементов, различающихся
некоторым признаком х.
Считается установленным (или проверенным
заранее), что распределения признака в
обеих совокупностях достаточно хорошо
описываются общими нормальными
распределениями вероятностей с одинаковой
дисперсией σ2
(она может быть и неизвестной). Проверяется
гипотеза о равенстве центров этих
нормальных распределений
(что вместе с уже принятыми предположениями
означает теперь полное совпадение
законов распределения). Проверяемая
гипотеза обычно называется
нуль-гипотезой.
Для ее проверки из каждой совокупности
берут случайную выборку, т. е. случайным
образом (как в лотерее) отбирают некоторое
количество элементов. Пусть количество
отобранных элементов (объем,
выборки)
из первой совокупности есть
n1
а
из второй — n2.
Подсчитываем средние значения признака
в каждой выборке, пусть эти средние
равны
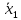 и
и
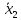 .
Если дисперсия
σ2
неизвестна, то подсчитываем еще и
эмпирические дисперсии
.
Если дисперсия
σ2
неизвестна, то подсчитываем еще и
эмпирические дисперсии
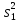 и
и
 .
.
В
предположении, что нуль-гипотеза верна,
отношения (2) и (3) представляют собой
случайные величины с вполне определенными
законами распределения. Поэтому, задавая
желаемую вероятность вывода
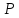 (например
0,99), мы
можем найти симметричный интервал (-
(например
0,99), мы
можем найти симметричный интервал (-
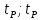 ), вероятность попадания в который равна
), вероятность попадания в который равна
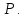 Другими словами, при справедливости
всех высказанных выше предположений и
нуль-гипотезы отношение (2) или (3) может
попасть в интервал(-
Другими словами, при справедливости
всех высказанных выше предположений и
нуль-гипотезы отношение (2) или (3) может
попасть в интервал(-
 ) случайно с вероятностью
) случайно с вероятностью
 Точки, лежащие вне этого интервала,
образуют
критическую область
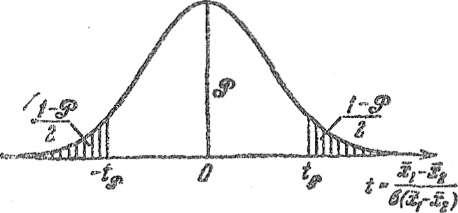
(заштрихованную на рис.),
Точки, лежащие вне этого интервала,
образуют
критическую область
(заштрихованную на рис.),
вероятность
попадания в которую составляет 1 -
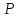 .
Значения
.
Значения
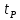 = t(
= t(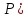 (при известной дисперсии) или
(при известной дисперсии) или
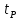 = t(
= t(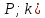 (при неизвестной дисперсии), определяющие
границы указанной доверительной области,
называются
критическими;
именно эти значения приведены в
(приложение, стр. 172 и 174).
(при неизвестной дисперсии), определяющие
границы указанной доверительной области,
называются
критическими;
именно эти значения приведены в
(приложение, стр. 172 и 174).
Если
отношение (2) или (3), подсчитанное по
значениям признака в выборках, попадет
в критическую область (т. е. если абсолютная
величина соответствующего отношения
превзойдет критическое значение из
табл. II или табл. IV), то нуль-гипотезу
отвергают
с надежностью
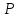 ,
т. е. считают, что результаты эксперимента
противоречат
нуль-гипотезе. В противном случае
нуль-гипотезу
принимают,
т. е. считают, что результаты эксперимента
не
противоречат
нуль-гипотезе (но, разумеется, не могут
служить и доказательством этой гипотезы).
,
т. е. считают, что результаты эксперимента
противоречат
нуль-гипотезе. В противном случае
нуль-гипотезу
принимают,
т. е. считают, что результаты эксперимента
не
противоречат
нуль-гипотезе (но, разумеется, не могут
служить и доказательством этой гипотезы).
Заметим,
что мы выбрали симметричный интервал
(-
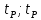 ) и, значит, симметричную критическую
область в связи с симметрией распределения
отношений (2) и (3) относительно нуля.
Возможен выбор и несимметричных
критических областей, например, в
задачах, где проверяемая гипотеза
a1
= a2
конкурирует
с гипотезой
а1
> а2
(а1
и
а2
- центры соответствующих распределений).
) и, значит, симметричную критическую
область в связи с симметрией распределения
отношений (2) и (3) относительно нуля.
Возможен выбор и несимметричных
критических областей, например, в
задачах, где проверяемая гипотеза
a1
= a2
конкурирует
с гипотезой
а1
> а2
(а1
и
а2
- центры соответствующих распределений).
Лекция 7.
Оценки точности измерений.
Точечные оценки дисперсии. Доверительные оценки средней квадратической ошибки.
Всюду
в дальнейшем предполагается, что ошибки
измерения являются случайными и
распределены по нормальному закону. В
качестве показателя точности измерений
(точности прибора) здесь оценивается
дисперсия этого закона σ2
или средняя квадратическая ошибка σ =
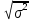 .
Измерения
предполагаются независимыми и равноточными
(с одной и тай же дисперсией).
.
Измерения
предполагаются независимыми и равноточными
(с одной и тай же дисперсией).
Точечные оценки дисперсии.
А. Если производятся измерения известной величине а (эталона), то в качестве эффективной оценки дисперсия применяют средний квадрат отклонения результатов измерений х1, х2, … хп от значения а:
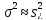 =
=
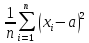 ,
(1)
,
(1)
Б. Если измеряют неизвестную величину, то в качестве оценки дисперсии применяют эмпирическую дисперсию
 ,
(2)
,
(2)
где
 -
среднее
арифметическое значение результатов
измерений. Оценка (2) является несмещенной
и состоятельной, но не является эффективной
(она является лишь асимптотически
эффективной, т. е. ее рассеяние стремится
к минимальному при неограниченном
увеличении числа измерений
п).
-
среднее
арифметическое значение результатов
измерений. Оценка (2) является несмещенной
и состоятельной, но не является эффективной
(она является лишь асимптотически
эффективной, т. е. ее рассеяние стремится
к минимальному при неограниченном
увеличении числа измерений
п).
В. Если одним и тем же прибором производят m серий измерений (вообще говоря, различных величин), то в качестве оценки дисперсии применяют взвешенное среднее из эмпирических дисперсий
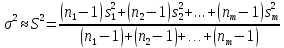 ,
(3)
,
(3)
где n1, n2, ... , nm — количества измерений в сериях;
 -
соответствующие
эмпирические дисперсии.
-
соответствующие
эмпирические дисперсии.
Оценка (3) обладает теми же свойствами, что и оценка (2), но практически позволяет использовать большее количество информации, что делает ее более надежной.
В частном случае, когда число измерений в каждой серии одно и то же: ni = n (i=l, ... ,т), оценка (3) принимает вид
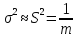
 (4)
(4)
т. е. здесь в качестве оценки дисперсии принимается среднее арифметическое значение эмпирических дисперсий.
Г. Если для m серий измерений одной и той же величины известны только количества измерений пх, пг пт и средние арифметические результаты х1, х2, ... , хт в каждой серии, то в качестве оценки дисперсии применяют эмпирическую дисперсию из средних
 =
=
 , (5)
, (5)
где
 ,
N
= n1
+ n2
+….+ nm
,
N
= n1
+ n2
+….+ nm
Эта
оценка является несмещенной и состоятельной
(а также асимптотически эффективной
при m
 ).
).
Д. Для интервального ряда данных (для группированных данных) величина среднего квадрата отклонения s*2 является смещенной оценкой дисперсии, причем ее смещение зависит от длины интервала h. Если длина интервала h достаточно мала (составляет не более десятой доли всего диапазона результатов измерений), то в качестве оценки дисперсии применяют исправленную эмпирическую дисперсию

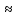 s*2
=
s*2
=
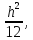 (6)
(6)
Здесь поправка -
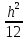 (поправка
Шеппарда) устраняет
главную часть смещения, так что оценку
(6) можно считать практически несмещенной.
(поправка
Шеппарда) устраняет
главную часть смещения, так что оценку
(6) можно считать практически несмещенной.
Пример. Для интервального ряда данных, был подсчитан средний квадрат отклонений от среднего значения s*2 = 0,052 6,58. Учитывая поправку Шеппарда - h2/12= = - 0,052/12 = - 0,052 0,08, получаем следующее значение исправленной эмпирической дисперсии:
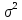
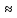 s*2
=
s*2
=
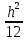 = 0,052 6,58
= 0,052 6,58
Во
всех указанных выше случаях
эмпирический стандарт
s =
 -
(эмпирическая средняя квадратическая
ошибка) дает
смещенную (несколько
преуменьшенную) оценку средней
квадратической ошибки
-
(эмпирическая средняя квадратическая
ошибка) дает
смещенную (несколько
преуменьшенную) оценку средней
квадратической ошибки
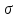 .
Смещение этой оценки зависит от числа
измерений n и уменьшается
с увеличением числа
п (так, при
п = 16 это смещение
составляет 2 %, а при n = 26
оно менее 1 %).
.
Смещение этой оценки зависит от числа
измерений n и уменьшается
с увеличением числа
п (так, при
п = 16 это смещение
составляет 2 %, а при n = 26
оно менее 1 %).
Доверительные
оценки средней квадратической ошибки.
При
большом числе измерений
доверительную оценку средней квадратической
ошибки σ записывают в виде оценки
относительного отклонения оцениваемого
значения σ от подходящего эмпирического
стандарта
s
(или s*,
S,
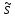 ,).
Такая оценка имеет вид
,).
Такая оценка имеет вид
|(σ - s)/s| < q,
или
s(1 - q) < σ < s(l + q), (7)
|
|
А |
Б |
В |
Г |
Д |
|
Эмпирический |
|
|
|
|
|
|
стандарт |
s* |
s |
S |
|
|
|
Число степеней свободы k |
n |
n - 1 |
N— т |
m - 1 |
п — 1 |
где значение коэффициента
q
= q( k)
находится по (приложение, стр. 175) в
зависимости от доверительной вероятности
k)
находится по (приложение, стр. 175) в
зависимости от доверительной вероятности
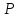 (надежности оценки)
и от
числа степеней свободы k.
Число степеней свободы равно числу
обрабатываемых результатов измерений,
уменьшенному на число связывающих их
линейных соотношений, т. е. оно зависит
не только от числа измерений, но и от
вида эмпирического стандарта, применяемого
для оценки σ. Число степеней свободы
определяется по табл. 1.
(надежности оценки)
и от
числа степеней свободы k.
Число степеней свободы равно числу
обрабатываемых результатов измерений,
уменьшенному на число связывающих их
линейных соотношений, т. е. оно зависит
не только от числа измерений, но и от
вида эмпирического стандарта, применяемого
для оценки σ. Число степеней свободы
определяется по табл. 1.
Здесь N = n1 + n2 +….+ nm число всех измерений в случае В.
Доверительная оценка для случая Д является весьма приближенной и может применяться только при достаточно большом числе n (не менее 50) и достаточно малой длине интервала h (не более 0,5 s*).
Заметим еще, что при достаточно большом числе k можно пользоваться и правилом трех сигм, которое в данном случае имеет вид
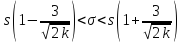 ,
,
надежность такой доверительной оценки превосходит
0,99 при k > 47,
0,992 при k > 100,
0,995 при k > 200.
При малом числе измерений симметричная оценка вида (7) приводит к неоправданно большим доверительным интервалам в силу резкой асимметрии распределения эмпирического стандарта (см. рис.).
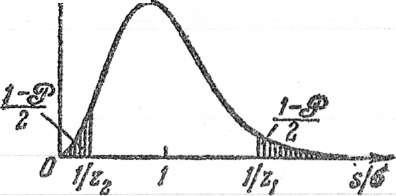
Поэтому
при малом числе измерений применяют
асимметричные доверительные оценки
вида sZl
< о < sZ2; значения
коэффициентов Z1
=Z1
(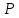 ,
k)
и
Zг
= Z2 (
,
k)
и
Zг
= Z2 (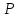 ,
k)
находятся
(приложение, стр. 176) в зависимости от
доверительной вероятности
,
k)
находятся
(приложение, стр. 176) в зависимости от
доверительной вероятности
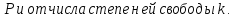
Лекция 8.
Сравнение дисперсий.
Сравнение двух дисперсий. Выделение большей дисперсии из многих.
При выполнении измерений в различных условиях возникает задача сравнения точности измерений. В частности, возникает задача сравнения точности различных измерительных приборов. Важность этой задачи особенно подчеркивается тем обстоятельством, что доверительные интервалы для средних квадратических ошибок оказываются обычно весьма широкими. Отметим также, что и в задачах сравнения средних иногда приходится сначала проверять равенство дисперсий.
Сравнение двух дисперсий. Пусть по результатам двух рядов измерений получены эмпирические дисперсии:
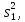 при
числе степеней свободы k1
при
числе степеней свободы k1
 при
числе степеней свободы
k2
при
числе степеней свободы
k2
Будем считать, что индекс 1 относится к большей эмпирической дисперсии.
Для решения вопроса о случайном или неслучайном расхождений дисперсий рассматривают отношение большей эмпирической дисперсии к меньшей
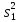 /
/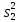 = F > l. (1)
= F > l. (1)
Затем
задают желаемую надежность вывода
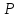 = 0,95 или
= 0,95 или
 = 0,99 по (прилож. стр. 177) находят критическое
значение отношения
F,
соответствующее данным числам степеней
свободы и k1 и k2
(напомним, что число степеней свободы
kt
относится к большей
эмпирической
дисперсии).
= 0,99 по (прилож. стр. 177) находят критическое
значение отношения
F,
соответствующее данным числам степеней
свободы и k1 и k2
(напомним, что число степеней свободы
kt
относится к большей
эмпирической
дисперсии).
Если
отношение (1), подсчитанное по результатам
измерений, оказывается больше критического
значения, то расхождение дисперсий
считают неслучайным
(значимым)
с надежностью
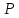 .
Другими словами, в этом случае точность
измерений существенно различна для
двух рядов измерений. В противном случае
для такого утверждения нет достаточных
оснований.
.
Другими словами, в этом случае точность
измерений существенно различна для
двух рядов измерений. В противном случае
для такого утверждения нет достаточных
оснований.
Точно так же поступают при проверке гипотезы о равенстве дисперсий. Если отношение (1), подсчитанное для двух выборок, оказывается больше критического значения, то гипотезу о равенстве дисперсий отвергают, в противном случае - принимают.
Пример.
Пусть старый измерительный прибор, на
котором произведено 200 измерений, имеет
точность, определяемую эмпирической
дисперсией
 =
3,82 (кв. единиц). Новый измерительный
прибор при первых пятнадцати измерениях
дал эмпирическую дисперсию
=
3,82 (кв. единиц). Новый измерительный
прибор при первых пятнадцати измерениях
дал эмпирическую дисперсию
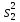 = 2,00 (кв. единиц). Можно ли считать, что
новый прибор дает существенно лучшую
точность, чем старый?
= 2,00 (кв. единиц). Можно ли считать, что
новый прибор дает существенно лучшую
точность, чем старый?
Решение.
Сравнение дисперсий по формуле (1) дает
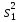 /
/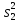 = F
= 1,91, причем числа степеней свободы
соответственно равны
= F
= 1,91, причем числа степеней свободы
соответственно равны
h1 = 200-1 = 199 и h2=15 - 1 = 14.
Так как полученное здесь отношение меньше критического даже при надежности 0,95 (что по табл. VII составляет более 2,13), те приведенные данные не дают оснований считать точность нового прибора лучшей, чем точность старого.
Для
окончательного решения вопроса надо
произвести большее число измерений
новым прибором. Если, например, при трех
сериях по пятнадцати измерений среднее
значение дисперсии останется тем же,
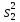 = 2,00, то, учитывая увеличение числа
степеней свободы до k2
= 3 14 = 42, мы найдем, что с надежностью 0,99
дисперсия нового прибора существенно
меньше дисперсии старого, т. е. точность
нового прибора выше.
= 2,00, то, учитывая увеличение числа
степеней свободы до k2
= 3 14 = 42, мы найдем, что с надежностью 0,99
дисперсия нового прибора существенно
меньше дисперсии старого, т. е. точность
нового прибора выше.
Выделение
большей дисперсии из многих.
Пусть среди нескольких приборов
(нескольких серий измерений) обнаружен
прибор (серия измерений), эмпирическая
дисперсия которого
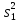 заметно больше остальных. Задача
заключается в том, чтобы выяснить, можно
ли считать отличие выделенной дисперсии
заметно больше остальных. Задача
заключается в том, чтобы выяснить, можно
ли считать отличие выделенной дисперсии
 от
остальных случайным или это отличие
следует считать существенным (значимым).
Для решения задачи поступают следующим
образом, Производят каждым из m
испытуемых приборов одинаковое число
n
измерений, подсчитывают эмпирические
дисперсии
от
остальных случайным или это отличие
следует считать существенным (значимым).
Для решения задачи поступают следующим
образом, Производят каждым из m
испытуемых приборов одинаковое число
n
измерений, подсчитывают эмпирические
дисперсии
 ,
,
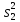 …
…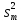 (
(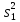 >
>
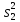 )
при i
> 1и сравнивают наибольшую дисперсию
)
при i
> 1и сравнивают наибольшую дисперсию
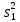 с
суммой всех
дисперсий
по формуле
с
суммой всех
дисперсий
по формуле
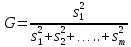 , (2)
, (2)
Если отношение (2) оказывается больше критического значения, приведенного в (прилож, стр. 178), то отличие первой дисперсии от остальных считается существенным, т. е. считают первый прибор (первую серию измерений) менее точным, чем остальные. В противном случае для такого утверждения нет достаточных оснований.
В
табл. критические значения отношения
G
приведены
для двух доверительных вероятностей
 = 0,95 и
= 0,95 и
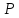 = 0,99 и для различных сочетаний чисел m
(числа приборов, серий измерений) и k
=n
-1
(числа степеней свободы).
= 0,99 и для различных сочетаний чисел m
(числа приборов, серий измерений) и k
=n
-1
(числа степеней свободы).
Пример. Пусть на шести приборах произведено по семи измерений, которые дали эмпирические дисперсии
3,82; 1,70; 1,30; 0,92; 0,78 и 0,81.
Сравнивая первую дисперсию с суммой всех дисперсий, вычисляем отношение (2): G = 0.41
Это
отношение оказывается меньше критического
значения при т
=
6 и k
= n
- 1 = 6
даже для доверительной вероятности
0,95 (таблица дает критическое значение
0,418). Поэтому нет оснований считать
дисперсию
 = 3,82 существенно больше остальных.
Заметим, что если бы такие же данные
встретились при
n
= 11
измерениях, то с надежностью, большей
0,99, можно было бы считать первую дисперсию
существенно больше остальных
(соответствующее критическое значение
при n
=10
и
= 3,82 существенно больше остальных.
Заметим, что если бы такие же данные
встретились при
n
= 11
измерениях, то с надежностью, большей
0,99, можно было бы считать первую дисперсию
существенно больше остальных
(соответствующее критическое значение
при n
=10
и
 = 0,99 составляет 0,408).
= 0,99 составляет 0,408).
Описанный
выше критерий применяется также и для
проверки
однородности
ряда дисперсий, т. е. для проверки того,
что все эмпирические дисперсии
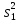 ,
,
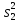 …
…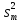 относятся
к выборкам из совокупностей с одной и
той же теоретической дисперсией σ2.
Если отношение (2) оказывается больше
критического значения, то надо считать,
что гипотеза об однородности ряда
дисперсий не согласуется с эмпирическими
данными,
относятся
к выборкам из совокупностей с одной и
той же теоретической дисперсией σ2.
Если отношение (2) оказывается больше
критического значения, то надо считать,
что гипотеза об однородности ряда
дисперсий не согласуется с эмпирическими
данными,

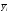
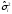
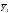
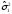
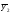

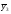
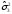
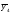
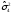
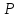 )/
q
)/
q