Анализ данных отчеты Катков / Analiz_dannykh_Lektsii_4

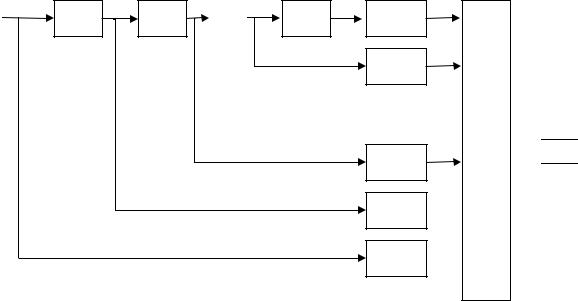
Чем старее данное, тем меньше её весовой коэффициент. Её отличительной осоденностью является то, что она включает в себя значения всего предыдущего периода, а не только скользящего интервала.

Не рекурсивный оператор СЭС

L−1

xсэс (l) =α∑β λ x(l −λ)

λ=0

L−1
Acac(Z) =α∑β λ Z −λ
λ=0
Z-1	Z-1	…	Z-1	BL-1
				BL-2

.

.

B2

B1

B0

M

α

Взвешенное скользящее среднее

Это ВСС отличается от простого САС тем, что каждому значению рассматриваемого интервала сглаживания придается вес, увеличивающийся к текущему значению, т.е. у первого значения вес равен 1 у следующего на единицу больше и т.д.

Произведение, полученное: в результате умножения величины на весовые коэффициенты суммируются и общие значения делятся на сумму весов.

			L
x		=	∑x(l) W (l)
	взв		l=`	, где
			L
			∑W (l)
			l=`

L- интервал сглаживания.

W(ℓ)-вес ℓ-того компонента.

В случае линейно взвешенных скользящих W=ℓ. Более позднему значению придается более больший вес.

Примеры взвешенного арифметического среднего и десятичными весами:

~

1

1

3

8

xl

=

xl

+

xl−1

+

xl−1

+

xl−3

2

4

16

16

~

= 0,4xl + 0,3xl−1

+ 0,2xl−1

+ 0,1xl−3

xl

Сумма всех весов должна быть равна единице

Рассеянно-экспоненциальное сглаживание

~	~		~		~				≤	β
			α[x(l) − xрэс (l−1)],		x(l) − xрэс (l−1)
x	рэс (l) = xрэс (l−1)	+	~				~			> β
		αβsign[x(l) − xрэс (l−1)],					x(l) − xрэс (l−1)

11

Х(ℓ)

β

α

~xрэс (l)

Z-1

α– аналогичен экспоненциальному среднему

α≈ L2+1;

β≈│∆х│+ (2÷3) δ

δ≈0,25D; D=xmax-xmin

│∆х│- максимальное приращение полезного сигнала на соседних отсчетах. При определение диапазона D выбросы не учитываются.

Медианное среднее

Медианна в качестве оценивания средних используется только в том случае, если закон распределения случайной величины близок к нормальному т.е предпосылка использования нормальный закон распределения.

Для любой монотонной последовательности (т.е.для любого вариационного ряда х(ℓ),ℓ=1..L) медианой или центральной величиной называют число М, смысле, что число членов предшествующих М, оказывается равным, числу следующих за ним членов.

Алгоритм оценивания медиан:

1)Проводится упорядочивание отсчетов по возрастанию или убыванию их значений т.е. выстраивается вариационный ряд;

2)При нечетных L выбирается центральное (срединное) значение из упорядоченной последовательности т.е.

xмс = x L2+1

3) При четных L определяется полу сумма из 2х средних членов вариационного ряда:

	1			L			L +1
xмс =		x				+ x
	2						2
				2

Этот алгоритм помехозащищенный

Зачем надо САС, СЭС, РЭС, МЭС?

САС запоминает данные всего ряда данных ,а для СЭС и РЭС только прошлое и вновь поступившее. Для нестационарных рядов данных САС сильно обращает внимание на прошлое. СЭС для нестационарных рядов данных. РЭС для нестационарных рядов данных при наличае помех импульсного типа. Релейная - это помеха защищенная. МЭС – при наличае групповых аномальных помех.

Сопоставляя, например оценки САС и оценки СЭС можно судить о степени не стационарности ряда данных по их статистическим характеристикам.

Виды случайных процессов

Ряд данных называется стационарным (в узком смысле слова) если его характеристики не меняются со временем.

12

На начальном этапе анализа рядов данных виз-на может предположить является исследуемый ряд стационарным по среднему и по дисперсии.

Выбор настроечного параметра α для СЭС, РЭС

4)Экспертная оценка;

5)Через расчет: двухкомпонентного критерия качества сглаживания и воспроизводимую оценку. Осуществляется по итерационной схеме:

a.Задается конкретное значение α = 0.1, 0.2, .. 0.9;

b.Исходный ряд х(ℓ) сглаживается с этим α;

c.Рассчитывается глаткостная составляющая двухкомпонентного критерия Q1:

		1	L		~	~	~
Q1	=		∑		x(l) −2x(l−1)		+ x(l−2)		- дискретный аналог второй производной.
		L −2 l=3

d.Расчет точностной составляющей двухкомпонентного критерия, которая характеризует близость тренда к исходному сигналу.

1

L

~

Q2 =

∑

x(l) − x(l)

L l=1

e. Расчет нормированных значений гладкостной составляющей и точностной составляющей.

max

1

L

~

~

~

Гладкостная: Q1

=

∑

x(l) − 2x(l −1) + x(l − 2)

L −

2 l=3

max

1 L

~

~

Точностная: Q2

=

∑

x(l) − xcp

, где

xcp - обще выборочное среднее.

L l=1

f. Осуществляется свертка гладкостной и точностной составляющих.

(1)Q = b Q * +b Q *,

Q * =

Q1

,

Q * =

Q2

Q max

1 1

2 2

1

Q max

2

1

2

b1,b2 – весовые коэффициенты, b1+b2 =1

b1=b2 =0.5

k = 1-Q

Q → min, k → max

Расчет по приведенному алгоритму приводится для всех значений α.

α

k

Из всех k выбирается максимальное и для соотвествующего α проводится серия расчетов по

0.1

k1

алгоритму с шагом 0.1

0.2

k2

Α=0.2 В качестве наилучшего параметра выбираем то значение, для которого получено мак-

*

*

*

*

симальное значение k по второй терации

0.9

k9

α

k

α

k

0.19

k1

0.21

k1

0.18

k2

0.22

k2

*

*

*

*

*

*

*

*

0.11

k9

0.29

k9

k

Хотелось бы

Реально

получить

k

(часть

α α

α

13

Если значение не удается определить наилучшим α по формуле (1), то можно использовать другие спо-
собы свертки.
Q2 = b1Q1* + b2 (Q2 * )2
Q3	= b1 Q1* + b2 (Q2* )3
Q4	= b	3 Q *	+ b		Q *
	1	1		2	2
Q5	= b	Q *	+ b	2	Q	*
	1	1			2
Q6	= b	4 Q *	+ b		Q *
	1	1		2	2

Статистические характеристики(II)

Коэффициент ковариации

Коэффициент взаимной ковариации – это показатель характеризующий наличие линейной связи между двумя статистическими величинами(?) при различных сдвигах между отсчетами.

		1	~	~
	Rxy (λ) =		[(x(l − λ) − x) − ( y(l) − y)]
		L − 2

х(ℓ),у(ℓ) – отсчеты временных рядов данных ~x, ~y - обще выборочные средние.

λ – сдвиг между отсчетами.

Если линейные связи между статистическими величинами отсутствуют, то коэффициент ковариации равен 0, но равенство нулю коэффициента ковариации не означает независимость статистических величин, т.к. статистические величины могут быть связанны по нелинейному закону.

-∞<Rxy<∞

т.к. диапазон широкий, то по значению Rxy можно судить только о наличие линейной связи и о её характере (+, -), но ничего неизвестно о силе этой связи.

Определив коэффициент ковариации с различными сдвигами λ = 0, ±1, ±2, ±3.

-4 -3 -2 -1 0 1 2 3 4	λ

Это набор коэффициентов ковариации определенных с различным сдвигом.

Коэффициент автоковариации

Коэффициент автоковариации – это показатель, характеризующий линейные связи между различными отсчетами одного ряда данных при различных сдвигах:

		1	~	~
	Rx (λ) =		[(x(l − λ) − x) − (x(l) − x)]
		L − 2

λ = 0 Rx(0 ) = Dx дисперсия.

14

Набор коэффициентов автокорреляции, определенных с различным сдвигом позволяет построить автокорреляционную функцию, она симметрична поэтому строится только для положительного λ.

Dx

1 2 3 4 λ

Коэффициент корреляции

Коэффициент взаимной корреляции – это показатель, характеризующий наличие линейных связей между двумя статистическими величинами (это нормированный коэффициент ковариации). Это мера тесноты линейной связи между статистическими величинами.

По его значению можно судить не только о наличие связи, но и о силе этой связи.

						1			~	~
rxy		(λ) =						[(x(l − λ) − x) − ( y(l) − y)]
					L − 2				δxδ y
λ – сдвиг между отсчетами.
L – объем выборки
δ		= D				=	1 L		~	2
	x		x					∑(x(l) − x )
							L l=1			- это СКО для статических величин х и у.
δ		= D				=	1 L		~	2
	y			y				∑	(y(l) − y )
							L l=1

−1 ≤ rxy ≤1

Для независимых статистических величин rxy= 0 – это не означает независимость статических величин. Чем сильнее │ rxy │→1, тем линейная связь сильнее.

При │ rxy │=1 наличие функциональной линейной связи между статическими величинами.

Если rxy > 0, то говорят о положительной корреляции, т.е. при увеличение одной статической величины другая СВ в среднем так же увеличивается. А при уменьшении – уменьшается.

Если rxy < 0, то говорят о отрицательной корреляции, т.е. при увеличение одной статической величины другая СВ в среднем убывает и наоборот.

Для выявления корреляционной связи между статистическими величинами на первом этапе можно построить корреляционное поле.

По коэффициентам корреляции, определяем с различными сдвигами λ можно построить взаимно корреляционную функцию.(ВКФ)

15

ВКФ позволяет также выявить наличие колебательной составляющей.

Коэффициент автокорреляции

Коэффициент автокорреляции – это мера тесноты линейной связи между различными отсчетами одного ряда данных.

				1				~	~
r		(λ) =					[(x(l− λ) − x)		−(x(l) − x)]
xy				L − 2				δx
λ – сдвиг между отсчетами.
L – объем выборки
δ		= D			=		1 L	~	2
	x		x				∑(x(l) − x )		- это СКО для статической величины х.
							L l=1

По набору коэффициентов автокорреляции определенных с различным сдвигом можно построить автокорреляционную функцию(АФК).

При λ = 0 rx(0 ) = 1

Если │ r │<0.3, то линейные связи практически отсутствуют. Если 0.3<│ r │<0.7;0.8, то говорят о линейной связи средней силы. │ r │>0.8 – сильная линейная связь.

Пример: Найти rx(ℓ) при λ = 2

х1) Определить обще выборочное среднее:

3	~		1
	x	=			37			= 3 . 7
1
			10
4						1		10
		2)		Dy =					∑(xl − 3.7)
2
					10 l=1
5
								~		~	~	~	~	~
6							1 (x1 − x)(x3			− x) + (x2	− x)(x4	− x) + (x3	− x)(x5	− x)
		3)		r(2) = 8							Dx
4
2
3
7

По виду АФК можно определить период колебательной составляющей статистической величины.

16

лог Rii Rjj.

Корреляционная матрица для совокупности n СВ представляет собой матрицу размерностью n x m, состоящую из парных коэффициентов корреляции единичной главной диагональю

Rii Rjj

, где Rij – алгебраическое дополнение элемента rij корреляционной матрицы, ана-

Если совокупность СВ содержит n рядов данных(n>3), тогда :

− Rij

rij /1,2,..,n =

Корреляционный анализ

Корреляционный анализ – это совокупность методов исследования параметров многомерной генеральной совокупности. Он позволяет с помощью выборки делать статистические выводы о различных мерах статистической линейной зависимости между признаками или различными отсчетами признака.

Z = f (x, y), y = f (x1 , x2 ,.., xn )

Частные и множественные коэффициенты корреляции

Частные коэффициенты корреляции

Частные коэффициенты корреляции – это мера линейной зависимости между двумя статистическими величинами(СВ) из некоторой совокупности статистических величин (x1, x2 ,.., xn ) при исключении

влияния остальных СВ.

Если у нас 3 ряда данных, n=3 х1, х2, х3. Надо определить:

1) Все парные коэффициенты корреляции ( r12, r23, r31);

2)	Частный коэффициент корреляции между 1 и 2 СВ, но без влияния 3:			r12	− r13 r23
				(1 − r		2 )(1 − r	2 )
				13		23
3)	r23 − r13 r12
	(1 − r	2 )(1 − r	2 )
	13	12
4)	r13 − r12 r23
	(1 − r	2 )(1 − r	2 )
	12	23

Для определения алгебраических дополнений Rij к элементу rij из исходной корреляционной матрицы вычеркивается i строка и j столбец.

Для получения матрицы размерностью n-1 x n-1 рассчитывается определитель, полученная результат домножают на (-1)ij.

1+r12r23r34r41+r13r24r31r42+r14r21r32r43-r41r32r23r14-r42·1r24·1-r43r34r21r12-1r31·1r13

−1 ≤ rчастн ≤1

Если СВ, входящие в совокупность попарно некорреляциированы, то все частные коэффициенты корреляции равны нулю.

Множественный коэффициент корреляции

Множественный коэффициент корреляции – это мера линейной зависимости между одной статистической величиной xi и линейной комбинацией из набора остальных СВ.

x1, x2, x3

17

r1/23 x1=ax2+bx3+c – линейная комбинация

Если n=3 (в совокупности 3 статистических величины), то

r			=	r	2	+ r	2	− 2r	r	r
	1			12		13		12	13	23
		23						2
						1	− r23
r			=	r	2	+ r	2	− 2r	r	r
				12		23		12	13	23 Диапазон изменения от 0 до 1.
2		13						2
						1	− r13
r			=	r	2	+ r	2	− 2r	r	r
	3			13		23		12	13	23
								2
		12				1	− r12
Если n > 3 rj/1,2,..,n = 1 -										∆
									R jj

∆ – определитель корреляционной матрици Rij – дополнение;

Множественный коэффициент корреляции не может быть меньше абсолютной величинв парного коэффициента корреляции или частного коэффициента корреляции с таким же первичным индексом. С увеличением набора исходных данных, входящих в совокупность, относительно которых определяется зависимость xj, его значение не уменьшается.

Если множественный коэффициент корреляции равен 1, то имеет место функция вида :

		n
x j	= ∑ai xi+b где аi, b - const
	1,2,..,n	i=1
		i≠ j
Если r j		= 0 , то вес СВ, входящей в совокупность попарно некоррелированны.
		1,2,..,n

Условное средние

Если в рассматриваемой системе существует связь между величинами, то из этих величин можно выделить зависимую переменную (определяемую) и независимую (определяющую).

В этом случае можно найти условное среднее для зависимой переменной внутри q-го интервала группированного по независимой переменной.

1)Определяется диапазон изменения независимой переменной.

2)Этот диапазон делится на интервалы.

3)Определяется значение независимой переменной, попавшие в данный интервал. Эти значения и есть условные средние.

	~		1	Lqx
	y	(qx ) =		∑ y( j, qx )
			Lqx
				j =1

qx =1, q

Lqx – количество данных, попавших в q интервал. y(j,qx) – j-ое значение переменной, попавшее в q группу.

Пример:

	x(ℓ)	y(ℓ)	0.97÷1.1
	1.02	23.5
	1.07	25
	1.1	24	0.97	0.99	1.1
	0.99	23.5
	0.97	29

qx =1				qx =2
[0.97÷0.99]				[0.99÷1.1]
23.5				23.5
29				25
				24
~		23.5 + 29		~		23.5	+ 25	+ 24
y(1)	=			y(2)	=
		2					3

18

Алгоритм определения корреляционного отношения через межгрупповую выборочную дисперсию.

Корреляционное отношение

Корреляционное отношение – это показатель тесноты связи между признаками при наличие между ними криволинейной (и линейной и нелинейной) зависимости.

Корреляционное отношение определяется по данным, сгруппированным по независимой переменной:

1)Выделяется зависимая и независимая переменная;

2)По зависимой переменной определяется средняя и обще выборочная дисперсия

				1			L	~	2
Dy		=					∑(y(l) − y )
					L l=1				L – объем выборки
~		1				L
y	=				∑y(l)
			L l=1

Dy - дисперсия.

~y - обще выборочное среднее.

3)Осуществляется группировка зависимой переменной по независимой переменной

4)Внутри каждой группы определяется условие среднее.

	~	1	Lqx
	y(λ, qx ) =		∑ y( j, qx )
		Lqx
			j =1

Lqx – количество данных попавших в q-ю группу

У(j,qx) – это j – e значение зависимой переменной в q-й группе. λ – сдвиг между отсчетами.

х	у
х1	у1
х2	у2
..	..
..	..

5)Определяется межгрупповая выборочная дисперсия, которые характеризует рассеивание условных средних ~y(λ, qx ) отнотельно обще выборочной среднего зависимой переменной

						2
	1	qx
					~	~
Dy (λ) =		∑			(y	(λ, qx ) − y ) Lqx
	L qx =1

q x - это общее количество групп

L - общее количество данных

6) Определяется корреляционное отношение .

	ηxy (λ) =	Dy (λ)	Это взаимо корреляционное отношение.
		Dy

Для корреляционного отношения, определяется с различным сдвигом, можно построить функцию. И из межгрупповой выборочной дисперсии, определенным с различным сдвигом можно построить взаимодисперсионную функцию.

Автокорреляционное отношение

Автокорреляционное отношение характеризует наличие криволинейной зависимости между различными отсчетами одного ряда данных.

1) Определяется общевыборочное среднее и общевыборочная дисперсия:

19

~		1				L
x	=				∑x(l)
			L l=1					~		L – объем выборки
					1		L		2
Dx		=					∑(x(l) − x )
					L l=1

2) Проводится группировка и определение условных средних:

	~		1	Lqx
	x	(λ, qx ) =		∑ x( j, qx )
			Lqx
				j =1

3) Определяется межгрупповая выборочная дисперсия:

						2
	1	qx
					~	~
Dx (λ) =		∑(x				(λ,qx ) − x ) Lqx
	L qx =1

4) Определяется автокорреляционное отношение:

D(λ)

ηx (λ) = Dx x

По значениям межгрупповой выборочной дисперсии, определенных с различным сдвигом, можно построить автодисперсионную функцию.

Свойства

Корреляционное отношение не симметрично по отношению к исследуемой переменной:

ηxy ≠ηyx

Корреляционное отношение изменяется от 0 до 1: 0 ≤η ≤1

Если η =1, то существует функциональная зависимость и если η = 0 , то это говорит об всякой связи

между СВ.

Корреляционное отношение не может быть меньше модуля коэффициента корреляции:

η = r

Если η ≈ r это свидетельствует о линейной связи.

Данный алгоритм позволяет получить правдоподобные оценки, если исходные выборки СВ достаточно велики (несколько сотен, тысяч) и количество интервалов не менее 8-10.

20