Анализ данных отчеты Катков / Analiz_dannykh_Lektsii_4

Элементы структурного анализа

Структурный анализ направлен на вскрытие внутреннего строения динамического сигнала путем его разделения на простые и структурно-однородные составляющие либо на построение таких характеристик ряда, анализ которого позволил бы своевременно распознать его особенности.

Структурный анализ опирается на динамическое оценивание разнообразных трендов с их наглядным представлением.

Критериальное определение тренда строится из следующих соображений:

1). Качественным показателем гладкости является сумма квадратов дискретного аналога 2ой производ-

ной. Для исходного ряда x(l) определяется вторые разности x(l)-x(l-1)-((x(l-1)-x(l-2)))=x(l)-2x(l-1)+x(l-2). 2). На ряду с гладкостью тренд должен отражать свойства исходного динамического сигнала. Количественной характеристикой близости тренда к исходному ряду может служить среднемодульное отклоне-

		1			L	~		1	L	~
	ние смо =				∑	x(l) − x(l)	либо среднеквадратичное отклонение СКО=		∑(x(l) − x(l))2
			l
					l =1			L l =1

Основные задачи структурного анализа

1). Выделение трендовой (низкочастотной составляющей ряда), наилучшим образом удовлетворяющим критерию, включающему 2 показателя (гладкости и точности). Эта трендовая составляющая называется условно-образующей кривой, играет роль учителя, а сглаженный ряд с выделением на нём особых точек нужен для отыскания оптимального настроечного параметра для различных алгоритмов структурного анализа.

Для построения условно-образцовой кривой можно использовать любые алгоритмы сглаживания (СЭС,РЭС,САС..)

Особая точка – точка, фиксирующая момент времени изменения направления основной тенденции сигнала, т. е. тренда.

2). Выбор методов структурного анализа и поиск их оптимальных настроечных параметров, т.е. таких значений, при которых координаты выделяемых особых точек на контрольных реализациях совпадали бы с координатами особых точек, построенных на условно-образующей кривой в смысле их СМО или СКО.

3). Проверка работоспособности методов с выбранными оптимальными настройками на других реализациях этой же исследуемой переменной и подготовка методов к испытанию в оперативном режиме.

Методы структурного анализа:

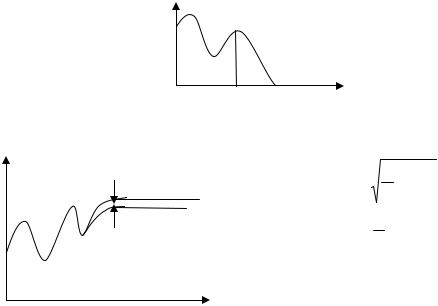
1). Разнотемповые сглаживатели. Основан на испытании двух или 3х разнотемповых скользящих средних. Рассмотрим два настроечных параметра α 1 и α 2, отличающиеся друг от друга в 2-4 и более раз.

0 ≤ α ≤1

В момент начала изменения тенденции разнотемповые сглаживатели дают расходящиеся сглаженные кривые; менее инерционная (меньше 2) быстро следует за изменением ряда, а более инерционная начинает отставать от исходного ряда и точка их пересечения позволяет выявить координату особой точки. Основной недостаток: выявление особых точек с запаздыванием.

2). Осцилляторы (колеблющаяся система)

а). момент – это осциллятор скорости рынка, в каждый момент времени он вычисляется, как разность между ценой закрытия сегмента дня и ценой закрытия m дней назад. M(l)=x(l)-x(l-m), осциллятор типа момент является опережающим индикатором, т.е. он перестаёт расти (падать), когда цены всё ещё растут при повышающимся тренде. (падают при понижающемся) и график момента меняет своё направление, когда тенденция начинает замедляться.

Т.к. тренды обычно снижают скорость перед тем, как изменить своё направление, осциллятор скор. Рынка, даёт предупреждение о том, что, возможно, надвигается смена изменения тенденции. Сигналами к действию служат понижения или повышения значений момента, относительно нуля. Положительный говорит об относительном росте цен. Отрицательный- о снижении цен.

21

Локальный Анализ:

Описание однородности структуры случ сигналов во времени осуществляется путём фиксирования особых точек, которые соотносятся с моментом наиболее значит. Изменения конкретных свойств случайных сигнала. Алгоритмы локального анализа позволяют определить моменты изменения свойств сигнала на основе анализа реализации соответствующих функционалов отличия: Ф(l)=F(l,l+l/2)-F(l-l/2,l).

Представляет собой разность значений некоторых характеристик объёмом в l/2значений. Введение функционалов отличия позволяет получить реализации информативных признаков, в том

смысле, что локальные экстремумы на графиках Ф(l), превышающие по своёму значению Зоны нечувствительности, позволяет определить местоположение и вид особых точек на реализации первичных данных.

при определении особых точек с помощью функционала отличия очень важно правильно выбрать длину скользящего окна L, эквивалентного двум смежным интервалам, длительностью L/2.

Алгоритм определения особых точек:

1). Постановка задачи исследования.

2). Выбор функционала отличия.

3). Расчёт реализации функционала.

4). Определение координат особых точек по реализации функционала.

5). Сравнение локальных экстремумов функционала с зоной нечувствительности. 6). Запоминание координат особых точек.

Конкретные алгоритмы функционала отличия:

1). Выделение момента ступенчатого изменения уровня сигнала x(l) можно осуществить на основе сравнения средних значений двух соседних участков x(l)

Разность средних уравнений ( или значений на соседних участках имеет более плавный характер по сравнению с графиком x(l), т.к. интегральный характер частично отфильтровать сильн. Колебания x(l) около среднего.

2). Моменты времени, когда происходит изменение тенденции и определ. Путем сопоставления углов наклона кусочно-линейн. Опроксимаций сигнала x(l) на соседних участках:

3). Скачкообразное изменение степени колебания исследуемой величины x(l) около тенденции может выглядеть следующим образом:

Этот информативный признак F3 представляет собой оценку дисперсии сигнала x(l) относительно его линейн. Аппроксимации уравнением: x(l)=a +bl на интервале L/2. Коэффициенты a и b определяются методом наименьших квадратов по L/2 точкам.

4). В качестве показателя гладкости отрезков сигнала x(l) можно использовать аналоги характеристик, примененных в теории сплайнов:

При построении функционала отличия Ф(l) можно их подвергнуть сглаживанию, исключив высокочастотную составляющую. Разложенные реализации исходного сигнала x(l) и функционалов отличия Ф(L), а также раздельное описание их структуры повышает эффективность определения координат особых точек:

Исходные алгоритмы определения информативности признаков и функционалов отличия можно усовершенствовать, рассматривая их в виде разности скользящих средних с вариантностью по объёму вы-

22

борки и путём перекрытия анализирующих участков, примыкающих к текущему моменту времени, т.е. берутся частично перекрывающиеся выборки, длительностью L и L/2.

В этом случае можно воспользоваться также экспоненциальным средним и РЭС, тогда:

Остальные аналогично.

Задача анализа временных рядов:

1.Идентификация 0 определение параметров систем, породившей этот временной ряд. В качестве параметров могут рассматриваться статистические характеристики, спектральные свойства и тд.

2.Прогнозпо данным наблюдений предсказать будущие значения систем.

Статистические модели

В основе многих статистических методов обработки лежит понятие статистичекой модели – это динамическая система с шумом. На такую систему действует некорреляционный шум ( с равномерным или нормальным значением распределения).

Т.к. предполагается, что известен только временной ряд для данных x1 x2 x3…xn,а шум можно создавать и представить в виде ряда данных S1…Sn, то можно предполагать, что i-ый элемент ряда данных есть некоторая функция от m предшествующих значений самой величины и шумовых величин.

Уравнение линейной авторегрессии:

A и b определяются методом наименьших квадратов.

Полученные a и b можно рассматривать, как решение задачи идентификации, а уравнение 2 можно использовать для прогноза будущих значений по m предыдущих. В качестве прогнозируемой величины можно использовать среднее значение, тогда уравнение 2 имеет вид:

При этом предполагается, что предшествующие значения известны точно. Шум является необходимой частью таких линейных моделей. В отсутствии шума поведение модели чаще всего абсолютно не похоже на исследуемый ряд, поэтому подобные модели можно использовать на малое число шагов вперед. В уравнении 1 функция F может быть и нелинейной, но в этом случае построение модели требует существенных затрат. Кроме того, нелинейные модели сами по себе могут порождать сложные временные последовательности. Нелинейные модели делятся на 2 типа:

1). Параметрические – такие модели, у которых функция F(X,S,A) одна и та же на всём диапазоне изменения величины x с постоянными коэффициентами А и задача состоит а том, чтобы эти коэффициенты наиболее точнее.

2). Непараметрические используют локальные аппроксимации в окрестности некоторого набора точек {Xk, Ek}. В этом случае функция F есть набор касочных аппроксимаций в окрестностях заданных узлов.

Алгоритмы прогнозирования таких моделей называются дискретными нелинейными предикторами.

Основной недостаток этих моделей (тип 1) : неясно имеют ли они отношения к действительным уравнениям динамических систем.

23

~		~			~		~	То для прогнозирования будущих значений можно использовать различные
xl	= xl−1				+ α(xl		− xl−1 )
					14243			формы (САС, СМС, СЭС, РЭС)
{СЭС}							εl
-ошибка прогноза.
~		~		−αεl
xl	= xl−1
ˆ	+λ	=	~	,	λ =	1,2,3
xl			xl

λ*

В качестве оценки точности прогноза чаще всего используется СКО или СМО

CKO =

1

L

ε

фактиче-

∑l=1

l

L

~

прогноз

ε

l =xl −xl

CMO =

1

∑L

εl

L l=1

Прогнозирование нестационарных показателей

Характеристика тренда

1)Тренд бывает линейным – это такой закон изменения среднего, при котором среднее возрастание или убывание со временем происходит по линейным зависимости.

2)Сезонный тренд – это такой закон изменения среднего, при котором среднее изменяется циклически в соответствие с некоторым временным циклом. При этом среднее за некоторый период по сравнению с со средним всего ряда может падать и подниматься.

3)Смешанные сезонно-линейные тренды

Линейные функции:
xl = µ + bl +εl	µ- среднее значение
b – скорость роста µ

εℓ- случайная ошибка с нулевым средним

Типы тренда

1) Аддитивный тренд В аддитивных трендах фактические значения отклоняются от среднего в положительную и отрица-

тельную сторону на одинаковый ω. 2) Мультипликативный тренд

Уменьшение или увеличение значения составляет приближенно одинаковый % относительно среднего определяемого характером среднего.

3) Комбинация аддитивного и мультипликативного тренда.

Алгоритмы:

Метод Холта

Метод Холта основан на оценке параметра мере степени линейного роста или падения показателя во времени. Фактор роста b оценивается как экспоненциальное среднее ~xl и предыдущее ~xl−1

Особенности метода.

24

				~	включает в себя значение прошлого показателя
Вычисление текущего экспоненциального среднего xl
роста bℓ-1, адаптируясь таким образом к предыдущему значению линейного тренда:
~	~	−bl−1 )		0 < A ≤1
xl = Ax + (1 − A)(xl−1			А-α вСЭС
~	~	+ B)bl−1		0 < B ≤1
bl = B(xl	− xl−1 ) + (1

После оценки значения показателя роста bℓ можно определить прогноз на τ моментов времени вперед xˆl+τ = ~xl + blτ τ называется горизонт прогноза

Недостаток: Два настроечных параметра (B должен быть ≈ 0.1А).

Модифицированный метод Холта

Доказано, что значение показателя роста bℓ совпадают с оценкой коэффициента линейного тренда по методу наименьшего квадрата, т.е. bℓ минимизирует сумму квадратов отклонений фактических значений xl от его тренда.

Если прогноз делается на достаточно большом промежутке времени, то

~	= Axl +					~
xl				(1 − A)xl−1
ˆ		= ~	+	bl (	1	+τ −	1)
					A
xl	+τ	xl

Метод двойного сглаживания Брауна

При линейном тренде простое экспоненциальное среднее всегда меньше на величину lag = 1 −a a b (за-

держка), где b – коэффициент роста в процессе. Дважды сглаженная оценка:

~	~	~
xl	= αxl	+ (1 − α ) xl−1
xˆl	= 2 xl	~
		− xl
В условиях устойчивости разность			~		~	можно считать постоянной и равной ≈	1−a	b , тогда
			x	−	x l
							a

прогноз на τ моментов времени вперед:

ˆ

=

ˆ

+

bl

τ

xl+τ

xl

α

~

~

bl =

(x

− xl )

1 −α

ˆ

=

~

− ~

+

α

~ − ~

τ

1

−α

xl+τ

2x x

(x xl )

Метод адаптивного сглаживания Брауна.

При прогнозировании необходимо учитывать старение данных, поэтому более свежие данные следует брать с большим весом, и тогда:

xl+τ = a0 + a1τ + a2τ 2 +εl

Следовательно εl - помеха, и а0, а1, а2 надо выбирать так, чтобы СКО фактического и прогнозируемого

значения был минимальным.

∑∞ γ i (xl−i − xˆl−i )2 → min

i=0

Т.е., а0, а1, а2 на момент времени ℓ выбираются так, чтобы взвешенная сумма квадратов значений стремилась к минимуму.

Для модели линейноаддитивного тренда оценка по взвешенному методу наименьших квадратов определялся:

25

xˆl +τ = xˆl + blτ

xl = xl−1 + bl−1 + (1 −γ 2 )εl

εl =xl − xˆl+τ

bl =bl−1 + (1 −γ)2εl

Достоинства:

Минимизируется взвешенная сумма квадратов ошибок прогнозирования. Один параметр γ=1-α

Коэффициент прогностической модели оценивается совместно, поэтому уменьшается их корреляция.

Метод Бикса-Дженкенса

~	~	+γ−1	(ε		−ε		) +γ0ε		+γ	0
xl	= xl−1					l−1				∑ε
				l				l		1l=−∞l

Член γ0 интерпретируется как коэффициент пропорциональный параметру управления; γ1- параметр управления; γ−1 - дифференциальный параметр управления (рекомендуется не использовать).

Метод Холта и Брауна является частным случаем метода Бокса-Дженкенся и все они совпадают, если

значения A , B , γ 0 , γ				1	, γ	− 1 связаны следующим образом:
A=γ0 =α(2 −α)
B =		α
	2	−α

γ0 =α2

Линейномультипликативная модель тренда

Метод Муира

Если среднее зависит от времени нелинейно, а пропорционально самому значению среднего, тогда

xl = (xl−1 +εl−1)ρ +εl
~						~
xl	= x + (1 −α)re xl −1
r	=α		xl		+ (1	−α)r
			~
e			xl−1			e −1
ˆ		= ˆ		τ
xl	+τ	xlre

re -несмещенная оценка мультипликативного коэффициента тренда.

Комбинация линейных и сезонно-аддитивных моделей тренда

При прогнозировании такого рода трендов используется декомпозиция сигнала, т.е. стационарность, линейность и сезонность разделяется и отдельно друг от друга. А окончательный прогноз осуществляется сложением прогнозов различных элементов.

При прогнозировании сезонного ряда необходимо определить как изменяется значение переменной в данный момент связанно с изменением значения этой переменной отстоящей на сезонный цикл. Каждый момент времени принадлежит одному циклу и задача заключается в установлении формы сезонной зависимости. Сезонные колебания описываются коэффициентом сезонностиэто отношение ожидаемо-

26

го значения величины к ее среднему значению, (соответствующие моменты времени лежащим внутри цикла).

Сезоннодекомпозиционная модель Холта-Виннера.

Основана на применении метода экспоненциального среднего: 1) Оценка стационарного фактора

Здесь используется то же уравнение, что и в методе Холта, при этом предполагается, что фактическое значение хℓ «очищено» от сезонной составляющей, делением его на коэффициент сезонности, соответствующее моменту времени ℓ-L

	~		xl	~	Fl−L - коэффициент сезонности.
	xl	= A		+ (1 − A)(xl−1bl−1 )
			Fl−L

2)Оценка линейного роста осуществляется на основе модели Холта: bl = B(~xl − ~xl −1) + (1 + B)bl −1

3)Оценка сезонного фактора:

		x					x
F	=	l		;	удобнее F	= C	l		+ (1 − C)F	0 < C ≤1
		~					~
l		x	l		l		x	l	l − L

4)Прогноз строится из трех элементов: оценки линии роста, оценки стационарного фактора, оценки сезонности.

xˆl +τ = (xˆl + blτ)Fl − L +τ

27