Konspekt

Лекция 1

Система отсчета. Материальная точка. Радиус-вектор и вектор перемещения, их связь с координатами точки. Траектория. Средняя и мгновенная скорости. Ускорение. Закон равноускоренного движения.

Положение тела в пространстве, так же как и перемещение может быть задано только

относительно какого-либо другого тела или системы тел. Так, например, относительно стенок вагона сидящий пассажир покоится, а относительно перрона двигается. Тело относительно, которого происходит определение положения рассматриваемого нами тела, называется телом отсчета. В действительности же помимо задания тела отсчета необходимо определить систему координат связанную с телом отсчета. Обычно принято выбирать декартову систему координат. Так как движение происходит не только в пространстве, но и во времени, то необходимо учитывать время при описании положения тела в пространстве. Это делается с помощью часов. Таким образом, совокупность тела отсчета, связанной с ним координатной системы и синхронизированных между собой часов образует систему отсчета.

Определив систему отсчета, можно приступать к описанию движения тела. Реальные движения тел настолько сложны, что, изучая их, необходимо отвлечься от несущественных для данного процесса деталей. Для этого применяется упрощение справедливость, которого определяется от конкретного рассматриваемого нами случая, от необходимой степени точности описания. Это бывает при рассмотрении ситуаций, когда размеры тела во много раз меньше прочих размеров, с которыми приходится иметь дело в условиях данной задачи. Тело размерами, которого можно пренебречь в условиях данной задачи называется материальной точкой. Вопрос можно ли рассматривать данное тело, как материальную точку определяется не самими размерами тела, а условиями задачи. Даже Землю в некоторых задачах можно рассматривать как материальную точку.

Положение материальной точки в пространстве можно определить с помощью радиус вектора. Радиус вектор r – это вектор проведенный из начала координат системы отсчета в место где находится материальная точка в данный момент времени.

При движении радиус вектор материальной точки изменяется как по модулю, так и по направлению r(t). Геометрическое место концов радиуса вектора r называется траекторией движения материальной точки. Пусть при своем движении материальная точка двигалась вдоль траектории из начального положения в конечное, тогда длина траектории называется путем s пройденным материальной точкой. Разница радиус векторов начального и конечного положений материальной токи называется перемещением Δr₁₂. Перемещение характеризует помимо самой величины еще и направление.

Всякое движение можно разложить на два вида: поступательное и вращательное. Поступательное движение – это движение, при котором любая прямая связанная с движущимся телом остается параллельной самой себе. В случае вращательного движения все точки тела движутся по окружностям центры, которых лежат на одной прямой, называемой осью вращения. Ось вращения может находиться и вне тела. В зависимости от формы траектории выделяют прямолинейное движение, движение по окружности и криволинейное движение. Поскольку, говоря о каком-либо теле как о материальной точки, мы пренебрегаем его размерами то понятие о вращении вокруг проходящей через него оси к таком телу не применимо.

При движении материальной точки за время Δt из начального положения в конечное ее перемещение составляет величину Δr. Тогда отношение Δr/Δt называют средним вектором скорости <v> за время Δt. Оказывается, что при достижении Δt достаточно малого значения средний вектор скорости <v> за этот промежуток времени перестает изменяться. Это означает, что при стремлении Δt к нулю средний вектор скорости <v> стремится к определенному пределу – этот предел называется скоростью материальной точки в данный момент времени v.

Модуль вектора скорости v определяется следующим способом:

Элементарный отрезок пути Δs не равен по величине модулю элементарного перемещения |Δr|, однако если брать эти величины за достаточно короткий промежуток времени, то различие между ними будет не велико и при стремлении Δt к нулю совсем исчезнет. Таким образом:

.

Путь, пройденный материальной точкой за промежуток времени от t1 до t2 равен определенному интегралу:

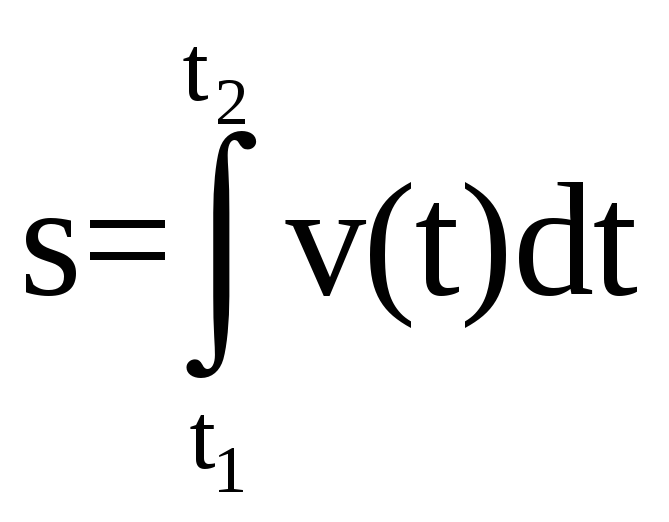
Если построить график зависимости модуль вектора скорости от времени то пройденный путь графически изображается, как площадь под графиком между двумя моментами времени.

Движение материальной точки характеризуется также ускорением. Вектор ускорения w определяет скорость изменения вектора скорости материальной точки со временем, т.е равен производной от вектора скорости по времени:

Направление вектора w совпадает с направлением вектора dv – приращением вектора v за время dt. Прямолинейное движение с постоянным ускорением называется равнопеременным. В зависимости от поведения скорости со временем различают равномерно-ускоренное и равномерно-замедленно движения.

Запишем проекции радиус вектора r(t) на оси X, Y, Z декартовой системы координат связанной с телом отсчета: x=x(t), y=y(t), z=z(t), тогда координатное представление радиус вектора выглядит следующим образом:

,

где е_x, e_y и e_z – единичные орты в направлении координатных осей. Зная зависимость этих координат от времени – закон движения, можно найти положение точки в каждый момент времени, ее скорость и ускорение. Действительно, взяв производную по времени от выражения для радиус вектора, получим:

.

Аналогично получаем координатное выражение для ускорения w:

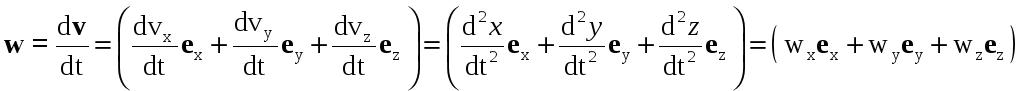
Из эти формул видно, что проекции векторов скорости и ускорения равны соответственно первой и второй производным координат по времени. Таким образов, зависимости x(t), y(t), z(t) по существу полностью определяют движение точки. Зная их можно найти не только положение точки но и проекции ее скорости и ускорения а следовательно, модуль и направление векторов v и w в любой момент времени. Например, модуль вектора скорости:

.

Кроме того, можно решить и ряд других вопросов: найти траекторию точки, зависимость пройденного ею пути от времени, зависимость скорости от положения точки и т.д.

Возникает и обратная задача: можно ли найти v(t) и r(t) зная зависимость от времени ускорения w(t). Оказывается, что для получения однозначного решения этой задачи недостаточно только зависимости w(t), необходимо так же знать начальные условия. Начальные условия определяют скорость v₀ и радиус-вектор r₀ материальной точки в начальный момент времени t=0. Рассмотрим случай движения материальной точки с постоянным ускорением w=const.

Сначала определим скорость материальной точки v(t). За промежуток времени dt элементарное приращение скорости dv=wdt. Проинтегрировав это выражение по времени от t=0 до t, найдем приращение вектора скорости за это время:

.

Но величина Δv – это еще не искомая скорость v. Чтобы найти v, необходимо знать скорость v₀ в начальный момент времени. Тогда v=v₀+Δv, или

.

Аналогично решается вопрос и о радиус-векторе r(t) материальной точки. За промежуток времени dt элементарное приращение радиус-вектора dr=vdt. Интегрируя это выражение с учетом найденной зависимости v(t), определим приращение радиус-вектора за время от t=0 до t:

.

Для нахождения самого радиус-вектора r(t) необходимо знать еще положение точки r0 в начальный момент времени. Тогда r=r₀+Δr, или

.

Итак, для полного решения задачи о движении материальной точки – определения ее скорости v и положения r в зависимости от времени – не достаточно знать зависимость w(t), еще необходимо знать и начальные условия.

Лекция 2

Движения тела по окружности. Угловая скорость, нормальное и тангенциальное ускорение. Движение по криволинейной траектории.

Введем единичный вектор τ, связанный с движущейся материальной точкой и направленный по касательной к траектории в сторону скорости. Таким образом, определенный вектор будет изменяться в зависимости от времени и координаты. Вектор скорости v материальной точки направлен по касательной к траектории, поэтом его можно определить следующим образом:

.

где v_τ – проекция вектора v на направление вектора τ, причем v_τ – величина алгебраическая. Величина v_τ равна модулю вектора v. Тогда ускорение материальной точки:

.

Последний член этого выражения можно преобразовать следующим образом:

.

где l – расстояние вдоль траектории от выбранного начала отсчета. Можно строго доказать, что при стремлении начальной и конечной точек траектории друг к другу отрезок траектории между ними стремится к дуге окружности с центром в некоторой точке. Эту точку называют центром кривизны траектории в данной точке, а радиус R соответствующей окружности - радиусом кривизны траектории в данной точке. Кривизна плоской линии в какой-либо ее точке равна кривизне окружности, сливающейся в данном месте с кривой на бесконечно малом ее участке.

,

причем при dl0 dτ_┴τ. Введя единичный вектор n нормали к траектории в точке, направленный к центру кривизны последнее выражение преобразуется к векторному виду следующим образом:

.

Окончательно получаем выражение для ускорения материальной точки:

.

Первое слагаемое в этом выражении называется тангенциальным ускорением w_τ, второе нормальным w_n:

.

Таким образом, полное ускорение w материальной точки может быть представлено как сумма двух векторов тангенциального и нормального ускорений. Один из, которых w_n перпендикулярен к вектору скорости v, а второй w_τ направлен по касательной к траектории. Если скорость растет по величине, то w_τ направлен в сторону движения материальной точки, если скорость убывает то w_τ направлен в сторону противоположную движению материальной точки. Тангенциальное ускорение характеризует изменение скорости по величине. Если скорость по величине не изменяется, тангенциальное ускорение равно нулю. Нормальное ускорение характеризует изменение скорости по направлению. Если направление скорости не изменяется, движение происходит по прямолинейной траектории. Кривизна прямой равна нулю, т.е. радиус кривизны R равен бесконечности, следовательно, нормальное ускорение равно нулю. Чем больше искривлена траектория, тем больше нормальное ускорение при той же величине скорости. Очевидно, что ускорение материальной точки, движущейся по произвольной кривой, также будет зависеть от кривизны траектории, которая в разных точках будет различна. Модуль полного ускорения:

,

где - производная модуля скорости по времени.

Предположим, что материальная точка движется вокруг неподвижной в данной системе отсчета оси по окружности радиуса r. Изменение положение материальной точки в пространстве можно определить по углу поворота за промежуток времени dt. Соответствующий угол поворота будем характеризовать вектором dφ, модуль которого равен углу поворота, а направление совпадает с осью вращения, причем так, что направление поворота отвечает правилу правого винта по отношению к направлению вектора dφ. Тогда элементарное перемещение материальной точки при таком повороте связано с углом поворота соотношением:

,

или в векторном виде

.

Данное равенство справедливо только, для бесконечно малого поворота dφ. При рассмотрении таких величин, как радиус-вектор, скорость, ускорение не возникал вопрос о выборе их направления: оно вытекало естественным образом из природы самих величин. Такие векторы называются полярными. В отличие от них векторы типа dφ, направление которых связывают с направлением вращения, называют аксиальными.

называется угловой скоростью тела. Вектор ω направлен вдоль оси, вокруг которой движется материальная точка, в сторону, определяемую правилом правого винта, и представляет собой аксиальный вектор. Модуль вектора угловой скорости равен. Вращение с постоянной угловой скоростью называется равномерным, при этом ω=φ/t. Таким образом, при равномерном вращении ω показывает, на какой угол поворачивается тело за единицу времени. Равномерное вращение можно характеризовать периодом обращения Т, под которым понимают время, за которое тело делает один оборот, т.е. поворачивается на угол 2π. Поскольку промежутку времени Т соответствует угол поворота 2π,

,

откуда период Т равен:

.

Число оборотов в единицу времени ν, равно:

.

Из предыдущего соотношения следует, что угловая скорость равна 2π, умноженное на число оборотов в единицу времени:

.

Понятие периода обращения и числа оборотов в единицу времени можно сохранить и для неравномерного вращения, понимая под мгновенным значением Т то время, за которое материальная точка совершила бы один оборот, если бы она равномерно двигалась по окружности с данным мгновенным значением угловой скорости, а под частотой понимая то число оборотов, которое совершила бы материальная точка за единицу времени при аналогичных условиях.

Вектор угловой скорости может изменяться, как по величине, так и по направлению. В первом случае изменяется значение вектора линейной скорости материальной точки, тогда как во втором случае изменяется ось вращения. Изменение вектора угловой скорости со временем характеризуют величиной называемой угловым ускорением:

.

Направление вектора β совпадает с направлением dω – приращения вектора ω. Вектор β, как и ω, является аксиальным. Единицей угловой скорости в СИ является радиан в секунду (рад/с), а единицей углового ускорения радиан на секунду в квадрате (рад/с²).

Очевидно что, зная радиус окружности, по которой движется материальная точка, угловую скорость, можно определить линейную скорость движения материальной точки по окружности. Для этого разделим в формуле, определяющей перемещения материальной точки, левую и правую части на dt. Так как dr/dt=v и dφ /dt=ω, то

т.е. скорость v материальной точки, вращающейся вокруг некоторой оси с угловой скоростью ω, равна векторному произведению ω на радиус вектор r материальной точки относительно центра окружности, по которой вращается материальная точка. Модуль вектора v равен v=ωr. Продифференцировав выражения связывающее угловую и линеную скорости найдем полное ускорение материальной точки: или

.

В рассматриваемом случае ось вращения неподвижна, поэтому вектор представляет собой тангенциальное ускорение w_τ. Вектор - это нормальное ускорение w_n. Модули этих ускорений равны:

.

Окончательно получаем модуль полного ускорения:

Лекция 3

Инерциальные системы отсчета, первый закон Ньютона. Сила. Второй закон Ньютона. Третий закон Ньютона. Преобразования Галилея.

В предыдущих темах рассматривалось движение материальной точки, не затрагивая вопроса о причинах движения – кинематика. В этом разделе рассмотрим движение материальной точки в связи с теми причинами (взаимодействиями), которые обуславливают тот или иной характер движения – динамика. Классическая динамика основана на трех законах сформулированных Ньютоном. Классическая ньютоновская динамика (механика) описывает обширный круг явлений. Однако существуют границы ее применимости. Классическая динамика применима при скоростях на много меньших скоростей света 3 10⁸ м/с и на расстояниях значительно больших атомных 10^-13см. Явления при больших скоростях получили объяснения в специальной теории относительности (Эйнштейн 1905 г.). Квантовая механика описывает явления, происходящие на атомарном и ядерном уровнях. В то же время надо понимать, что классическая механика не перечеркивается новыми теориями, а следует из специальной теории относительности в пределе больших масс и малых скоростей.

Первый закон Ньютона формулируется следующим образом: всякое тело находится в состоянии покоя или равномерно и прямолинейно движется, пока воздействие со стороны других тел не заставит его изменить это состояние. Оба этих состояния характеризуются тем, что ускорение тела равно нулю. Формулировке первого закона можно придать следующий вид: скорость любого тела остается постоянной, пока воздействие на это тело со стороны других тел не вызовет ее изменение.

Первый закон Ньютона выполняется не во всякой системе отсчета. Например, рассмотрим две системы отсчета, которые движутся друг относительно друга с некоторым ускорением. Если относительно одной из систем материальная точка покоится, то относительно другой движется с ускорением. Таки образом, первый закон Ньютона не может выполняться одновременно в обеих системах. Система отсчета, в которой выполняется первый закон Ньютона, называется инерциальной. Система отсчета в которой первый закон Ньютона не выполняется называется неинерциальной системой отсчета. Любая система, движущаяся относительно инерциальной системы отсчета прямолинейно и равномерно тоже будет инерциальной. Следовательно, существует не одна, а бесконечное множество инерциальных систем.

Для инерциальных систем справедлив принцип относительности, согласно которому все инерциальные системы по своим механическим свойствам эквивалентны друг другу. Это значит, что никакими механическими опытами, проводимыми внутри системы, нельзя установить, покоится эта система или движется. Данное утверждение составляет содержание принципа относительности Галилея.

Как же преобразуются координаты и скорости материальной точки при переходе от одной инерциальной системы отсчета к другой. Пусть инерциальная система К’ движется со скоростью V относительно другой инерциальной системы К. Выберем оси координат x’, y’, z’ K‘-системы параллельно соответствующим осям x, y, z К-системы так, чтобы оси x’ и x совпадали между собой и были направлены вдоль вектора V. Взяв за начало отсчета времени момент, когда начала координат О’ и О совпадали, запишем соотношение между радиус-векторами r’ и r одной и той же материальной точки в K’- и К-системах:

и, кроме того,

.

Здесь подразумевается, что длина отрезков и ход времени не зависят от состояния движения и, следовательно, одинаковы в обеих системах отсчета. В координатах преобразования Галилея имеют вид:

Продифференцировав по времени преобразования Галилея, найдем классический закон преобразования скорости материальной точки при переходе от одной инерциальной системы отсчета к другой:

.

Дифференцируя это выражение по времени с учетом того, что V=const, получаем w’=w, т.е. ускорение точки одинаково во всех инерциальных системах отсчета.

Рассматривая процесс изменения скорости, понимаем, что всякое изменение скорости

тела, связано с воздействием на него других тел. Влияние другого тела или тел, вызывающее ускорение тела (изменение скорости), называют силой. Следовательно, причиной ускорения тела является действующая на него сила.

Опыт показывает, что всякое тело оказывает сопротивление при любых попытках изменить его скорость – как по модулю, так и по направлению. Это свойство, выражающее степень сопротивления тела изменению его скорости, называют инертностью. Мерой инертности служит величина, называемая массой.

Понятие массы m, вводится по определению отношений масс двух различных тел по обратному отношению ускорений, сообщаемых им равными силами:

Видно, что такое определение не требует предварительного измерения самих сил. Достаточно лишь удовлетворить условием равенства сил. Таким образом, сравнение масс двух тел, на которые действует одна и та же сила, сводится к сравнению ускорений этих тел. Взяв некоторое тело за эталон массы, мы имеем возможность сравнить массу любого тела с этим эталоном. Единицей массы СИ является килограмм (кг). В рамках ньютоновской механики масса обладает следующими двумя важнейшими свойствами:

1. масса – величина аддитивная, т.е. масса составного тела равна сумме масс его частей;

2. масса тела как такового – величина постоянная, не изменяющаяся при его движении.

Второй закон Ньютона формулируется следующим образом: ускорение всякого тела прямо пропорционально действующей на него силе и обратно пропорционально массе тела.

Он, так же как первый закон Ньютона, справедлив только в инерциальных системах отсчета. Воздействие одних тел на другие имеет направленный характер. Следовательно, сила является векторной величиной. Опыт показывает, что если на тело действуют несколько сил, то результирующая сила F определяется следующим образом:

т.е. силы F₁ F₂ … подчиняются принципу суперпозиции.

Во всех случаях, когда в опытах участвуют два тела А и В и тело А сообщает ускорение телу В, обнаруживается, что и тело В сообщает ускорение телу А. Отсюда мы заключаем, что действия тел друг на друга имеют характер взаимодействия. Ньютон постулировал общее свойство всех сил взаимодействия третьим законом Ньютона: силы, с которыми две материальные точки действуют друг на друга, всегда равны по модулю и направлены в противоположные стороны вдоль прямой, соединяющей эти точки, т.е.

Это значит, что силы взаимодействия всегда появляются парами. Обе силы приложены к разным материальным точкам и, кроме того являются силами одной природы. Третий закон Ньютона распространяется и на системы из произвольного числа материальных точек. В третьем законе Ньютона предполагается, что обе силы равны по модулю в любой момент независимо от движения точек. Это утверждение соответствует допущению о мгновенности распространения взаимодействий – допущению, которое называется принципом дальнодействия.

В соответствии с принципом относительности Галилея законы механики одинаковы во всех инерциальных системах отсчета. Это значит, что уравнение, определяющее силу, будет иметь один и тот же вид в любой инерциальной системе отсчета. Чтобы свести нахождение закона движения частицы к чисто математической задаче, необходимо, прежде всего, знать зависимость силы от определяющих ее величин. Такие зависимости являются следствием обобщения результатов опыта. Наиболее часто встречаемые силы это гравитационные, электрические, сила упругости, сила трения скольжения, однородная сила тяжести.

Сила гравитационного притяжения, действующая между двумя материальными точками в соответствии с законом всемирного тяготения имеет вид:, где γ – гравитационная постоянная.

Кулоновская сила действующая между двумя точечными зарядами q₁ и q₂ , где r – расстояние между зарядами k - коэффициент пропорциональности, зависящий от выбора системы единиц.

Однородная сила тяжести F=mg.

Упругая сила – сила, пропорциональная смещению материальной точки из положения равновесия и направленная к положению равновесия: F=-χr, где r – радиус-вектор, характеризующий смещение материальной точки из положения равновесия; χ – положительный коэффициент, зависящий от упругих свойств среды.