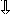- •Примеры вычисления вероятности.
- •Замечание. Двойной критерий применим и тогда, когда распределение генеральной совокупности отлично от нормального, но не очень ассиметрично.
- •Приложение а Кумулятивные биноминальные вероятности
- •Приложение б
- •Куммулятивные пуассоновские вероятности.
- •Значения для различныхи m
- •Значения для различныхи m
- •Учебное пособие
- •654007, Г. Новокузнецк, ул. Кирова 42.
- •Применение статистических методов в управлении качеством
Замечание. Двойной критерий применим и тогда, когда распределение генеральной совокупности отлично от нормального, но не очень ассиметрично.
Проверка гипотезы о дисперсии
нормально распределенной генеральной совокупности.
Методы проверки дисперсии имеют особую важность при анализе точности и стабильности технологических процессов, измерительных приборов и станков.
Рассмотрим пример:
На автоматическом станке выпускается
массовая продукция – шатунные пальцы
двигателя. Из партии деталей взята
выборка объемом n
= 20 и произведены измерения диаметров
каждого пальца, по которым рассчитаны
статистические характеристики:
![]() = 20 мм,
= 20 мм,![]() = 841 µкм2,
= 841 µкм2,
![]() = 29 µкм. Контролер по опыту знает точность
(а тем самым и
= 29 µкм. Контролер по опыту знает точность
(а тем самым и![]() как меру рассеивания станка) при
производстве пальцев. Она лежит в
пределах ± 20 µкм. Можно ли по результатам
выборки заключить, что станок дает
допустимый разброс для данной партии,
или же значение
как меру рассеивания станка) при
производстве пальцев. Она лежит в
пределах ± 20 µкм. Можно ли по результатам
выборки заключить, что станок дает
допустимый разброс для данной партии,
или же значение![]() = 29 µкм указывает на несоответствие
станка предъявляемым требованиям?
= 29 µкм указывает на несоответствие
станка предъявляемым требованиям?
Последовательность
решения такой задачи выглядит обычно
следующим образом: Предлагают, что
выборка взята из генеральной совокупности
с нормальным распределением и
характеристиками μ
и
![]() .
Тогда решение вопроса о том, обеспечивает
ли станок допустимый разброс, эквивалентно
решению о том, что выборка взята из
совокупности с
.
Тогда решение вопроса о том, обеспечивает
ли станок допустимый разброс, эквивалентно
решению о том, что выборка взята из
совокупности с![]() = 20 µкм, т.к. стандартное отклонение
= 20 µкм, т.к. стандартное отклонение![]() представляет собой меру однородности
продукции.
представляет собой меру однородности
продукции.
Проверяемая
гипотеза гласит:
![]() ,
или в общем виде:
,
или в общем виде:![]() ,
если
,
если![]() заранее задано. Среднее значениеμ
генеральной совокупности при этом может
оставаться неизвестным.
заранее задано. Среднее значениеμ
генеральной совокупности при этом может
оставаться неизвестным.
Опровержение гипотезы H0 указывает контролеру на необходимость наладки станка, т.к. процесс имеет недопустимый разброс.
Гипотеза H0
проверяется по выборочной характеристике
![]() :
:
![]()
![]() ,
(7.23)
,
(7.23)
которая удовлетворяет
![]() распределению
с m
= n
− 1 степенями свободы, если гипотеза H0
верна. При
вероятности ошибки α
критическое значение
распределению
с m
= n
− 1 степенями свободы, если гипотеза H0
верна. При
вероятности ошибки α
критическое значение
![]() определяется из соотношения:
определяется из соотношения:

![]() (7.24)
(7.24)
Критическая область неприятия гипотезы H0 определяется неравенством:
 .
(7.25)
.
(7.25)
В этом случае
гипотеза отвергается, т.е. выборка взята
не из нормально распределенной генеральной
совокупности с дисперсией
![]() .
При выполнении неравенства
.
При выполнении неравенства гипотеза принимается. Критические
значения
гипотеза принимается. Критические
значения![]() для различныхα
и m
представлены
в приложении Ж.
для различныхα
и m
представлены
в приложении Ж.
Для нашего примера находим:
![]()
Для α
= 0,01 и m
= 19 находим по таблице приложения Ж
![]() .
Ввиду того, что
.
Ввиду того, что![]() гипотезаH0
отвергается.
Станок не обеспечивает требуемой
точности. Необходимо отыскать и устранить
причины.
гипотезаH0
отвергается.
Станок не обеспечивает требуемой
точности. Необходимо отыскать и устранить
причины.
Проверка гипотезы о значениях двух дисперсий
из нормально распределенных генеральных совокупностей.
Имеются две
независимые выборки объемом n1
и n2
с выборочными
характеристиками соответственно:
![]() ,
,![]() и
и![]() ,
,![]() .
Необходимо проверить предположение,
что генеральные совокупности, из которых
взяты выборки, имеют одинаковые дисперсии:
.
Необходимо проверить предположение,
что генеральные совокупности, из которых
взяты выборки, имеют одинаковые дисперсии:![]() .
.
Проверка гипотезы
о равенстве дисперсий
![]() заключается в следующем. Для проверки
используется выборочная характеристика
заключается в следующем. Для проверки
используется выборочная характеристика ,
которая соответствуетF-распределению
Фишера, с m1 = n1 − 1
и m2 = n2 − 1
степенями свободы.
,
которая соответствуетF-распределению
Фишера, с m1 = n1 − 1
и m2 = n2 − 1
степенями свободы.
Критическая область
для одностороннего ограничения (![]() )
определяется выражением:
)
определяется выражением:
![]() (7.26)
(7.26)
При расчете F в числителе надо ставить большую выборочную дисперсию.
Метод проверки,
т.н. «F-критерий»
формулируется так: при
 − гипотезаH0
отвергается,
т.к. расхождение между выборочными
дисперсиями
− гипотезаH0
отвергается,
т.к. расхождение между выборочными
дисперсиями
![]() и
и![]() являются значимыми. В случае же
являются значимыми. В случае же![]() − гипотеза принимается.
− гипотеза принимается.
Значение
![]() для различныхα
и (m1,
m2)
степеней свободы можно найти в таблицах
(приложение И).
для различныхα
и (m1,
m2)
степеней свободы можно найти в таблицах
(приложение И).
Проверка гипотезы
о законе распределения генеральной совокупности.
Проверка гипотезы о нормальном распределении
При планировании
и проведении выборочного контроля по
количественному признаку полагают, что
контролируемый параметр имеет точно
или приближенно нормальное распределение
с математическим ожиданием
![]() и дисперсией
и дисперсией![]() .
.
Однако на практике встречаются случаи, когда это условие не выполняется. Поэтому необходимы методы проверки, которые бы позволяли решить по выборке является ли генеральная совокупность нормально распределенной или нет.
В математической статистике разработано несколько таких методов, из которых наибольшее практическое применение имеют критерии согласия Колмогорова и Пирсона.
Рассмотрим метод,
основанный на использовании критерия
![]() ,
известного как критерий согласия
Пирсона.
,
известного как критерий согласия
Пирсона.
Последовательность проверки гипотезы состоит в следующем:
Исследуется выборка из генеральной совокупности достаточно большого объема n.
Измеряется значение параметра качества, и результаты измерений оформляются в виде интервального ряда.
Применение критерия Пирсона является обоснованным, если ни одна из разрядных частей не будет мала. Для этого следует объединять разряды так, чтобы минимальная по величине разрядная часть была бы не менее пяти (
 )
)
Выдвигается нулевая гипотеза, что генеральная совокупность имеет нормальное распределение с функцией распределения
 и параметрами
и параметрами
 и
и :
:
 .
Параметры
.
Параметры
 и
и в общем случае неизвестны.
в общем случае неизвестны.Проверка гипотезы осуществляется на основе критерия:
![]() ,
(7.27)
,
(7.27)
который, согласно
Пирсону, приближенно удовлетворяет
![]() распределению сm
степенями свободы при истинности
гипотезы
распределению сm
степенями свободы при истинности
гипотезы
![]() .
В работах по математической статистике
можно найти доказательства этого
утверждения.
.
В работах по математической статистике
можно найти доказательства этого
утверждения.
В выражении (7.27) k
– количество интервалов интервального
ряда;
![]() – частота j-того
интервала значений параметра х;
– частота j-того
интервала значений параметра х;
![]() – теоретическая частота j-того
интервала значений х.
– теоретическая частота j-того
интервала значений х.
Находятся статистические характеристики выборки
 и
и
 .
.При расчете теоретических частот распределения учитывают, что
 есть вероятность того, что наблюдаемая
случайная величинах
генеральной совокупности попадает в
j
– ый интервал, т.е. х
располагается между верхней (
есть вероятность того, что наблюдаемая
случайная величинах
генеральной совокупности попадает в
j
– ый интервал, т.е. х
располагается между верхней ( )
и нижней (
)
и нижней (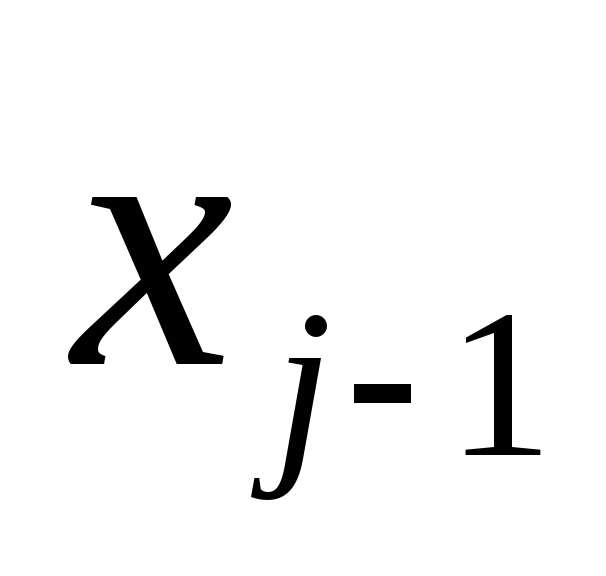 )
границамиj-того
интервала (рисунок 7.6).
)
границамиj-того
интервала (рисунок 7.6). Производится переход к нормированной случайной величине:
![]() ,
(7.28)
,
(7.28)
где
![]() − верхняя границаj-того
интервала.
− верхняя границаj-того
интервала.
Тогда:
 (7.29)
(7.29)
где
![]() – функция распределения нормированного
нормального распределения случайной
величины U,
численные значения которой представлены
в приложении Д. При этом верхняя граница
j−1-ого
интервала равна нижней границе j-того
интервала.
– функция распределения нормированного
нормального распределения случайной
величины U,
численные значения которой представлены
в приложении Д. При этом верхняя граница
j−1-ого
интервала равна нижней границе j-того
интервала.
Все расчеты оформляются в следующей таблице:
Таблица
7.1 − Результаты расчетов критерия
![]()
|
Интервал
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |

Рисунок 7.6 − Площадь по кривой Гаусса между верхней
и нижней границами j-го интервала
Рассчитывается![]()
![]() ,
как сумма последнего столбца таблицы.
,
как сумма последнего столбца таблицы.
Выбирается вероятность ошибки
 .
.Решают вопрос о числе степеней свободы m. Если
 и
и генеральной совокупности известны, тоm
= k
- 1, где k
– число интервалов. В противном случае
(
генеральной совокупности известны, тоm
= k
- 1, где k
– число интервалов. В противном случае
(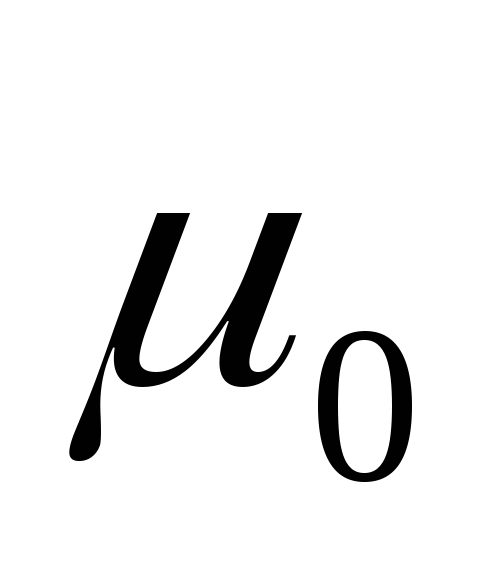 и
и неизвестны) − m =k
- 3.
неизвестны) − m =k
- 3.При вероятности ошибки
 критическое значение
критическое значение определяется
из соотношения:
определяется
из соотношения:
 ,
(7.30)
,
(7.30)
где критическое
значение
![]() находят по таблице в приложении Ж.
находят по таблице в приложении Ж.
Соотношение
 означает отклонение гипотезы
означает отклонение гипотезы
![]() .
.
Проверка гипотезы о распределении
генеральной совокупности по закону Пуассона
Критерий
![]() находит применение не только в связи с
проверкой нормального распределения
генеральной совокупности. Его можно
использовать и для проверки гипотез о
том, что данная выборка взята из
генеральной совокупности, распределенной
по биномиальному закону или по закону
Пуассона. Именно эти законы предполагаются
у контролируемого параметра качества
при планировании и проведении выборочного
контроля по альтернативному признаку.
находит применение не только в связи с
проверкой нормального распределения
генеральной совокупности. Его можно
использовать и для проверки гипотез о
том, что данная выборка взята из
генеральной совокупности, распределенной
по биномиальному закону или по закону
Пуассона. Именно эти законы предполагаются
у контролируемого параметра качества
при планировании и проведении выборочного
контроля по альтернативному признаку.
Рассмотрим случай проверки гипотезы о том, что выборка объема n взята из генеральной совокупности, удовлетворяющей закону Пуассона. В этом случае выдвигается нулевая гипотеза:
![]() (7.31)
(7.31)
с параметром m (математическое ожидание).
Для того чтобы
использовать критерий
![]() ,
необходимо получить по значениям выборки
оценку не указанного гипотезой
,
необходимо получить по значениям выборки
оценку не указанного гипотезой
![]() параметра m
распределения Пуассона, а также рассчитать
теоретические частоты
параметра m
распределения Пуассона, а также рассчитать
теоретические частоты
![]() .
.
Известно из
математической статистики, что пригодной
оценкой математического ожидания
генеральной совокупности является
среднее арифметическое выборки
![]() :
:![]() .
Теоретические частоты вычисляются
следующим образом:
.
Теоретические частоты вычисляются
следующим образом:
![]() ,
(7.32)
,
(7.32)
где
![]() − теоретическая вероятность того, что
в выборке объемом n
случайное событие произойдет ровно r
раз.
− теоретическая вероятность того, что
в выборке объемом n
случайное событие произойдет ровно r
раз.
Вероятности
![]() для
некоторых значенийm
и r
затабулированы в таблице, представленной
в приложении Б. Если в результате оценки
получится нетабулированное значение
m,
расчет теоретических частот можно
производить по следующей рекурентной
формуле:
для
некоторых значенийm
и r
затабулированы в таблице, представленной
в приложении Б. Если в результате оценки
получится нетабулированное значение
m,
расчет теоретических частот можно
производить по следующей рекурентной
формуле:
![]() (7.33)
(7.33)
с начальным членом
![]() .
При определении критического значения
.
При определении критического значения
![]() число степеней свободы равноm
= k
2.
число степеней свободы равноm
= k
2.
Контрольные вопросы
Что означает статистическая проверка гипотезы?
Какие выборочные характеристики используются при статистической проверке гипотез?
 характеристика
и особенности ее распределения?
характеристика
и особенности ее распределения?t характеристика и особенности ее распределения?
F характеристика и особенности ее распределения?
Как проверяется гипотеза о среднем значении нормально распределённой генеральной совокупности при известной дисперсии?
Особенности проверки гипотезы о среднем значении нормально распределённой генеральной совокупности при неизвестной дисперсии?
Особенности проверки гипотезы о значениях двух средних из нормально распределенных генеральных совокупностей. Случай зависимых выборок?
Особенности проверки гипотезы о значениях двух средних из нормально распределенных генеральных совокупностей. Случай независимых выборок?
Проверка гипотезы о дисперсии нормально распределенной генеральной совокупности?
Проверка гипотезы о значениях двух дисперсий из нормально распределенных генеральных совокупностей?
Проверка гипотезы о нормальном законе распределения генеральной совокупности?
Проверка гипотезы о распределении генеральной совокупности по закону Пуассона?
Задачи для самостоятельной работы
На рабочем месте выборочно проводится хронометраж и фиксируется время выполнения рабочим определенной операции с целью сделать выводы о равномерности его работы. При выборке объема n = 9 вычислены статистические характеристики:
 = 83 мин, S2
= 4,04 мин2.
Мерой равномерности работы можно
считать дисперсию S2.
= 83 мин, S2
= 4,04 мин2.
Мерой равномерности работы можно
считать дисперсию S2.
Необходимо проверить, существенно ли отличается дисперсия 4,04 мин2 данного рабочего от дисперсии S2 = 3мин2, рассчитанной на основании большого числа измерений продолжительности одной и той же операции. Вероятность ошибки возьмите равной 0,05.
Точность работы станка-автомата проверяется по дисперсии контролируемого размера изделий, которая не должна превышать
 .
Взята проба из 25 случайных отобранных
изделий, по результатам измерений
которых получены следующие данные:
.
Взята проба из 25 случайных отобранных
изделий, по результатам измерений
которых получены следующие данные:
|
Контролируемый размер, хi |
3,0 |
3,5 |
3,8 |
4,4 |
4,5 |
|
Частота, hi |
2 |
6 |
9 |
7 |
1 |
Требуется при уровне значимости 0.05 проверить, обеспечивает ли станок требуемую точность.
Из нормальной генеральной совокупности деталей извлечена выборка объемом n = 21 и по ней найдена дисперсия контролируемого параметра S2=16,2. Требуется при уровне значимости 0,01 проверить нулевую гипотезу:

При оценке индекса возможности процесса обработки деталей на станке исходят из дисперсии, равной 0,18. При очередном контроле технологического процесса была взята выборка объемом n = 31 и получены следующие результаты измерений:
|
хi |
10,1 |
10,3 |
10,6 |
11,2 |
11,5 |
11,8 |
12,0 |
|
hi |
1 |
3 |
7 |
10 |
6 |
3 |
1 |
Исходя из уровня значимости 0,05, оцените, соответствует ли технологический процесс требуемому уровню точности.
Из нормальной генеральной совокупности извлечена выборка объемом n = 8 и по ней найдена дисперсия S2 = 0,25. Проверьте нулевую гипотезу
 при уровне значимости 0,05.
при уровне значимости 0,05. Для проверки точности двух шлифовальных станков проведены измерения толщины обрабатываемых на них одинаковых деталей. По результатам n1 = 25 измерений деталей со станка №1 получено стандартное отклонение S1 = 7,98 μкм, а по результатам n2 = 30 измерений деталей со станка №2 – S2 = 5,71 μкм. Можно ли на основании этих результатов при вероятности ошибки 0,05 сказать, что точность станка №2 выше точности станка №1?
Для сравнения удельного веса кирпичей из двух зон обжига печи (А и В) отобрали и взвесили n1 = 14 кирпичей из зоны А и n2 = 10 кирпичей из зоны В. Обработка результатов взвешивания дала следующие значения дисперсий: S12 = 16,4 (кг/м3)2 для зоны А и S22 = 22,5 (кг/м3)2 для зоны В. Следует ли на основании этих результатов при уровне значимости 0,05 говорить, что разброс удельных весов кирпичей не зависит от зоны их обжига в печи.
Производилось сравнение точности химического анализа у двух лаборантов, один из которых (А) был новичком в работе, а другой (В) опытным работником. Лаборант А выполнил 20 анализов, а лаборант В − 13 анализов одного и того же вещества. Обработка результатов этих анализов дала следующие значения статистических характеристик:
 ,
ЅА2
= 0,0295; ЅВ2
= 0,0139. Оцените профессиональные качества
новичка, взяв в качестве уровня значимости
0,05.
,
ЅА2
= 0,0295; ЅВ2
= 0,0139. Оцените профессиональные качества
новичка, взяв в качестве уровня значимости
0,05.Для сравнения точности двух станков-автоматов взяты две выборки, объемы которых n1 = 10 и n2 = 8. По результатам измерений деталей выборки получены следующие данные:
|
Станок №1 |
1,08 |
1,10 |
1,12 |
1,14 |
1,15 |
1.25 |
1,36 |
1,38 |
1,40 |
1,42 |
|
Станок №2 |
1,11 |
1,12 |
1,18 |
1,22 |
1,33 |
1,35 |
1,36 |
1,38 |
|
|
Можно ли считать, что станки обладают одинаковой точностью при вероятности ошибки 0,01.
Используя критерий Пирсона при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности Х с эмпирическим распределением выборки объемом n=100, представленной ниже:
|
|
3-8 |
8-13 |
13-18 |
18-23 |
23-28 |
28-33 |
33-38 |
|
|
6 |
8 |
15 |
40 |
16 |
8 |
7 |
Расчеты дали
следующие значения статистических
характеристик этого ряда:
![]() .
.
Используя критерий Пирсона при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности Х с эмпирическим распределением выборки объемом n=200, представленной ниже:
|
|
3-5 |
5-7 |
7-9 |
9-11 |
11-13 |
13-15 |
15-17 |
17-19 |
19-21 |
|
|
15 |
26 |
25 |
30 |
26 |
21 |
24 |
20 |
13 |
Расчеты дали
следующие значения статистических
характеристик этого ряда:
![]() .
.
В механическом цехе с 10 станками ежедневно в определенное время проводилась регистрация количества простаивавших станков Х. Всего было проведено 200 таких наблюдений, результаты которых приведены в таблице:
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
41 |
62 |
45 |
22 |
16 |
8 |
4 |
2 |
0 |
0 |
0 |
Используя критерий Пирсона при уровне значимости 0,05 проверить, подтверждает ли эта выборка предположение о том, что количество отказавших станков в генеральной совокупности удовлетворяет распределению Пуассона.
ИНТЕРВАЛЬНАЯ ОЦЕНКА
Общие положения
Оценка неизвестного
параметра качества по выборке одним
числом называется точечной оценкой. Но
полученная при этом величина имеет
случайный характер и может отличаться
от действительного параметра. Особенно
это актуально при малых объемах выборки.
Поэтому возникает задача определения
точности и надёжности оценки. Требуется
знать к каким ошибкам может привести
замена параметра
![]() его точечной оценкой
его точечной оценкой![]() (например,
(например,![]() )
с какой степенью уверенности можно
ожидать, что эти ошибки не выйдут за
известные пределы.
)
с какой степенью уверенности можно
ожидать, что эти ошибки не выйдут за
известные пределы.
Пусть для параметра
![]() получена из опыта смещённая оценка
получена из опыта смещённая оценка![]() .
Мы хотим оценить возможную при этом
ошибку. Назначим некоторую достаточно
большую вероятность γ, например γ = 0,9;
0,95; 0,99. Говорят, что событие с вероятностью
γ можно считать практически достоверным.
.
Мы хотим оценить возможную при этом
ошибку. Назначим некоторую достаточно
большую вероятность γ, например γ = 0,9;
0,95; 0,99. Говорят, что событие с вероятностью
γ можно считать практически достоверным.
Найдем значение ε, для которого
![]() .
(8.1)
.
(8.1)
В этом случае
диапазоны возможных значений ошибки,
возникающей при замене
![]() на
на![]() ,
будет
,
будет![]() ε.
Большие по абсолютной величине ошибки
будут появляться только с малой
вероятностью
ε.
Большие по абсолютной величине ошибки
будут появляться только с малой
вероятностью
![]() .
.
Перепишем (8.1) в следующем виде:
![]() .
(8.2)
.
(8.2)
Равенство (8.2)
означает, что с вероятностью γ
неизвестное значение параметра
![]() попадает в интервал
попадает в интервал
![]() .
(8.3)
.
(8.3)
Вероятность γ
называют доверительной
вероятностью,
интервал
![]() доверительным
интервалом,
границы интервала:
доверительным
интервалом,
границы интервала:
![]() и
и![]()
доверительными границами (рисунок 8.1).
доверительными границами (рисунок 8.1).

Рисунок 8.1 – Доверительный интервал
Перейдем к вопросу
о нахождении доверительных границ
![]() и
и![]() .
Способ их нахождения зависит от того,
знаем ли мы закон распределения случайной
величины генеральной совокупности, её
параметры
.
Способ их нахождения зависит от того,
знаем ли мы закон распределения случайной
величины генеральной совокупности, её
параметры![]() ,
,![]() и др., закон распределения выборочного
параметра
и др., закон распределения выборочного
параметра![]() и т.п.
и т.п.
Доверительные интервалы для параметра

нормально распределенной генеральной совокупности
Делается допущение,
что закон распределения случайной
величины в генеральной совокупности
является нормальным с математическим
ожиданием
![]() и дисперсией
и дисперсией![]() .
Пусть
.
Пусть![]() известна из опыта, а параметр
известна из опыта, а параметр![]() -неизвестен.
-неизвестен.
При построении
доверительных интервалов для
![]() можно исходить из тех же предпосылок,
что и при определении статистических
критериев проверки гипотез, т.к. эти
методы тесно связаны между собой.
можно исходить из тех же предпосылок,
что и при определении статистических
критериев проверки гипотез, т.к. эти
методы тесно связаны между собой.
Как было показано
ранее в подразделе 7.3, для проверки
гипотезы
![]() указывается критическая область, или
область неприятия гипотезы
указывается критическая область, или
область неприятия гипотезы![]() задаваемая неравенством:
задаваемая неравенством:
![]() .
(8.4)
.
(8.4)
Значения
![]() находятся для заданной вероятности
ошибки
находятся для заданной вероятности
ошибки![]() (уровня значимости) по формулам (7.6) или
(7.8). Область, в которой гипотеза
(уровня значимости) по формулам (7.6) или
(7.8). Область, в которой гипотеза![]() не подлежит опровержению и для которой,
таким образом, выборочный результат не
противоречит выдвинутой гипотезе,
даётся выражением:
не подлежит опровержению и для которой,
таким образом, выборочный результат не
противоречит выдвинутой гипотезе,
даётся выражением:
![]() .
(8.5)
.
(8.5)
Можно задаться
обратным вопросом, как следует выбрать
гипотезу
![]() (т.е.
(т.е.![]() ),
чтобы при наличии выборки объёмаn
она не была опровергнута.
),
чтобы при наличии выборки объёмаn
она не была опровергнута.
Такая обратная
постановка задачи путём решения
неравенства (8.5) относительно
![]() даёт интервал для
даёт интервал для![]() вида1):
вида1):
![]() .
(8.6)
.
(8.6)
Выражение (8.6) даёт значение доверительного интервала и его границ:
нижняя граница:
![]() ;
(8.7)
;
(8.7)
верхняя граница:
![]() ;
(8.8)
;
(8.8)
ширина интервала:
![]() .
(8.9)
.
(8.9)
Следует отметить,
что границы интервала являются случайными
величинами т.к. выборочная функция
![]() принимает в выборках различные значения.
принимает в выборках различные значения.
Если за основу
берётся одностороннее ограничение, то
находится только верхняя, либо только
нижняя доверительная граница, в
зависимости от выбора критической
области для гипотезы
![]() .
Например,:
.
Например,:
![]() и
и
![]() ,
или
,
или
![]() и
и
![]() .
.
Если неизвестны
не только среднее значение
![]() ,
но и дисперсия
,
но и дисперсия![]() генеральной совокупности, то заданные
формулами (8.7), (8.8) доверительные границы
заменяются границами:
генеральной совокупности, то заданные
формулами (8.7), (8.8) доверительные границы
заменяются границами:

1) Здесь
![]() заменено символом
заменено символом![]() для того, чтобы подчеркнуть, что этот
параметр неизвестен.
для того, чтобы подчеркнуть, что этот
параметр неизвестен.
![]() ,
(8.10)
,
(8.10)
![]() .
(8.11)
.
(8.11)
где
![]() найдено
по распределению Стьюдента для уровня
значимости
найдено
по распределению Стьюдента для уровня
значимости![]() и
числа степеней свободы
и
числа степеней свободы![]() .
.
Ширина доверительного интервала:
![]() (8.12)
(8.12)
зависит от желаемой
доверительной вероятности![]() (
(![]() ),
величины выборочной дисперсии
),
величины выборочной дисперсии![]() и объёма выборкиn.
и объёма выборкиn.
Чем больше n,
тем уже интервал, т.е. тем выше степень
точности утверждения. Доверительный
интервал, задаваемый формулами (8.10),
(8.11) в общем случае шире интервала по
формулам (8.7), (8.8) при равных n
и
![]()
Пример. Проведено 145 испытаний предела текучести низколегированной стали (n=145). Обработка данных выборки дала следующие результаты:
![]() ,
,
![]() .
.
Для уровня значимости 0,01 найти доверительные границы и доверительный интервал.
Решение. Для
![]() =0,01
находим:
=0,01
находим:![]() и по формулам (8.10), (8.11):
и по формулам (8.10), (8.11):
![]() ,
,
![]() .
.
Т.о.
![]() и
и![]() .
.
Предположим,
заказчика интересует более узкий
доверительный интервал для той же
доверительной вероятности
![]() ,
например
,
например![]() .
Надо определить количество измерений
для выполнения этого условия.
.
Надо определить количество измерений
для выполнения этого условия.
Из (8.12) записываем:
![]() =0,80,
=0,80,
откуда:
![]() .
.
Т.е. для выборки
объёмом 442 средний предел текучести
ожидается в интервале от 31,0 до 31,80
![]() .
.
Доверительные интервалы для параметра

нормально распределенной генеральной совокупности.
За основу берём
статистическую проверку гипотезы
![]() При использовании двухстороннего
ограничения интервал, в котором гипотеза
не отвергается, запишется следующим
образом (рисунок 8.2):
При использовании двухстороннего
ограничения интервал, в котором гипотеза
не отвергается, запишется следующим
образом (рисунок 8.2):
![]() ,
,(8.13)
откуда:
![]() .
(8.14)
.
(8.14)

Рисунок 8.2 – К
определению доверительного интервала
для ![]()
Выражение (8.14) даёт
доверительный интервал для ![]() .
.
Доверительные
границы для ![]() из (8.15) запишутся следующим образом:
из (8.15) запишутся следующим образом:
![]() ;
;
![]() .
(8.15)
.
(8.15)
Контрольные вопросы
Ч
то такое интервальная оценка?
Что такое доверительная вероятность?
Что такое доверительный интервал?
Что такое доверительные границы?
Как находятся доверительные интервалы для параметра
 нормально распределенной генеральной
совокупности?
нормально распределенной генеральной
совокупности?
Как находятся доверительные интервалы для параметра
 нормально распределенной генеральной
совокупности?
нормально распределенной генеральной
совокупности?
ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ
МЕЖДУ ПАРАМИ СЛУЧАЙНЫХ ПЕРЕМЕННЫХ
Общие положения
Практический интерес представляет случай, когда измеряются два различных признака качества Х и Y. При этом могут возникать следующие варианты:
Оба признака Х и Y тесно связаны друг с другом ( например, сторона и площадь квадрата). Этот вид связи называется функциональным. Зависимость между обоими признаками выражается в виде формулы. Если задано значение одного признака, то по этой формуле можно найти значение другого признака.
Оба признака не строго связаны друг с другом. В этом случае отдельно взятому значению признака Y может соответствовать ряд распределения значений Х. Если это распределение значений Х не изменяется с изменением величины Y, то оба признака Х и Y не зависят друг от друга.
Если для каждого фиксированного значения признака Y получают распределение значений признака Х, и наоборот, для каждого фиксированного значения признака Х получают распределение признака Y, то между обоими признаками имеется связь. При этом связь между признаками является не математической, а статистической.
На практике часто бывает важным изучить зависимость между парами соответствующих случайных переменных.
Например, предел текучести σт и предел прочности σв стального проката есть случайные величины, со своими законами распределения. Есть ли связь между ними и какая. Зависит ли случайная величина размер детали от изменения скорости вращения шпинделя и как зависит.
Эти две переменные могут быть:
характеристикой качества и влияющим на нее фактором (диаметр детали и скорость вращения шпинделя);
двумя различными характеристиками качества (σт и σв стали);
двумя факторами, влияющими на одну характеристику качества (форма углового шва и содержание углерода в наплавленном металле – факторы; твердость шва – характеристика качества).
Для того, чтобы в целом оценить зависимость между парами измеряемых признаков строят диаграмму рассеивания в координатах х‑у. и подсчитывают коэффициент корреляции.
Диаграмма рассеивания
Для построения диаграммы берется выборка парных данных объемом, по крайней мере, n=30. При построении диаграммы следует придерживаться следующих рекомендаций:
для построения диаграммы рассеивания шкалы на вертикальной и горизонтальной осях выбирают так, чтобы длины рабочих частей получились примерно одинаковыми. В этом случае диаграмму легче читать.
если одна измеряемая величина является фактором, а другая – характеристикой качества, то фактор следует откладывать по оси абсцисс (горизонтальной).
Пример построения диаграммы рассеивания для механических характеристик проката из различных сталей по выборке объемом n=60 приведен на рисунке 9.1.

Рисунок 9.1 Диаграмма рассеивания для значений σт и σв
различных сталей
Как читать диаграммы рассеивания
По диаграмме рассеивания можно оценить обычно основные закономерности распределения пар. В первую очередь надо обратить внимание на далеко отстоящие точки – выбросы (рисунок 9.2 а). Можно предположить, что эти точки либо результат ошибки измерений, либо обусловлены какими-либо неслучайными факторами. Такие точки следует исключить из корреляционного анализа. Следует найти причины таких выбросов и устранить их.
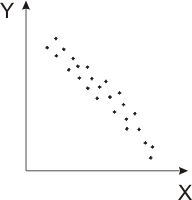
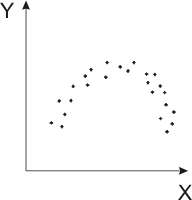
Возможны различные варианты скоплений точек на диаграммах рассеивания. Основные варианты представлены на рисунке 9. На рисунке 9.2а и 9.2б величина Y растет с ростом Х это положительная корреляция. Причем на рис. 9.2а эта тенденция выражена ярко и говорит о сильной положительной корреляции. На рисунках 9.2г и 9.2д с ростом X значение Y уменьшается – это отрицательная корреляция. На рисунке 9.2е приведен пример, когда между X и Y нет никакой определенной связи, так что можно говорить об отсутствии корреляции. На рисунке 9.2ж показан пример нелинейной корреляции, когда при изменении X значение Y сначала увеличивается, затем убывает.
Вычисление числовых характеристик
двух измеряемых признаков
Для большей наглядности и упрощения последующих расчетов, полученные при измерении данные целесообразно оформить в виде корреляционной таблицы. В качестве примера приведем таблицу значений пределов текучести σт и пределов прочности σв полученных на выборке объемом n=60 (таблица 9.1).
Таблица 9.1 – Корреляционная таблица
|
σв признак Y |
Yj среднее |
σт признак Х |
hj | ||||||||||||
|
30-50 |
50-70 |
70-90 |
90-110 |
110-130 |
130-150 |
150-170 | |||||||||
|
Xi (среднее значение интервала) | |||||||||||||||
|
40 |
60 |
80 |
100 |
120 |
140 |
160 | |||||||||
|
190-210 |
200 |
|
|
|
|
|
|
2 |
2 | ||||||
|
170-190 |
180 |
|
|
|
|
|
|
2 |
2 | ||||||
|
150-170 |
160 |
|
|
|
|
|
5 |
|
5 | ||||||
|
130-150 |
140 |
|
|
1 |
1 |
5 |
2 |
|
9 | ||||||
|
110-130 |
120 |
|
|
1 |
8 |
4 |
|
|
13 | ||||||
|
90-110 |
100 |
|
1 |
7 |
6 |
|
|
|
14 | ||||||
|
70-90 |
80 |
3 |
3 |
4 |
|
|
|
|
10 | ||||||
|
50-70 |
60 |
5 |
|
|
|
|
|
|
5 | ||||||
|
hi |
|
8 |
4 |
13 |
15 |
9 |
7 |
4 |
| ||||||
-

а)

б)

в)
г)

д)

е)
ж)
а) диаграмма рассеивания с выбросами; б) сильная положительная корреляция; в) может быть положительная корреляция; г) сильная отрицательная корреляция; д) может быть отрицательная корреляция;
е) отсутствие корреляции; ж) нелинейная корреляция.
Рисунок 9.2 – Различные типы диаграмм рассеивания
Для каждого измеряемого признака можно вычислить его среднюю арифметическую и выборочную дисперсию:
![]() ,
(9.1)
,
(9.1)
![]() ,
(9.2)
,
(9.2)
![]() ,
(9.3)
,
(9.3)
![]() .
(9.4)
.
(9.4)
При наличии повторяющихся значений данных и результатов, представленных в виде интервального ряда (таблица 9.1) эти формулы будут несколько отличаться согласно разделу 4.
Однако, в первую очередь, интерес представляет форма связи между признаками X и Y и сила (теснота) связи.
Информацию об этом дают следующие характеристики:
Sxy ковариация;
rxy коэффициент корреляции.
Ковариация ряда измерений из n пар значений (X1Y1), (X2Y2),…, (XnYn) равна:
![]() .
(9.5)
.
(9.5)
Как видно из (9.5)
ковариация Sxy
может быть как положительной, так и
отрицательной. Например, для малых
значений
![]() разность
разность![]() отрицательна, а для больших – положительна.
То же самое относится и к значениям
отрицательна, а для больших – положительна.
То же самое относится и к значениям![]() .
Таким образом, отрицательная ковариация
позволяет заключить, что большим
значениям
.
Таким образом, отрицательная ковариация
позволяет заключить, что большим
значениям![]() соответствует преимущественно малые
значения
соответствует преимущественно малые
значения![]() и наоборот.
и наоборот.
«Нормируя» Sxy с помощью стандартных отклонений получают коэффициент корреляции:
 .
(9.6)
.
(9.6)
Коэффициент
корреляции rxy
есть мера силы (тесноты) и направления
линейной связи между значениями
![]() и
и![]() .
По определению он может приносить любые
значения от -1 до +1:
.
По определению он может приносить любые
значения от -1 до +1:
![]() .
(9.7)
.
(9.7)
Если rxy
= 0, то линейная связь между признаками
![]() и
и
![]() отсутствует.
Если же, наоборот,
отсутствует.
Если же, наоборот,
![]() ,
то между обоими признаками существует
линейная функциональная связь. Если
,
то между обоими признаками существует
линейная функциональная связь. Если
![]() ,
то связь прямая ( с ростом
,
то связь прямая ( с ростом
![]() увеличивается
и
увеличивается
и
![]() ).
Если
).
Если
![]() ,
то связь обратная (с ростом
,
то связь обратная (с ростом
![]() значения
значения
![]() уменьшаются).
В зависимости от величины коэффициента
корреляции можно сделать следующие
заключения :
уменьшаются).
В зависимости от величины коэффициента
корреляции можно сделать следующие
заключения :
![]() –практически
нет связи ;
–практически
нет связи ;
![]() –слабая связь;
–слабая связь;
![]() –средняя связь;
–средняя связь;
![]() –сильная связь;
–сильная связь;
![]() –практически
функциональная связь.
–практически
функциональная связь.
Для нашего примера из таблицы 9.1 в результате вычислений получены следующие значения:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Таким образом, можно сказать, что в данном случае имеется сильная положительная корреляция между σт и σв, то есть, стали с большим пределом текучести, как правило, обладают и высоким пределом прочности.
Метод суждения о существовании корреляции с помощью построения диаграммы рассеивания и вычисления коэффициента корреляции называется корреляционным анализом.
Некоторые практические замечания о корреляционном анализе
Плохой выбор размерностей координатных осей может существенно исказить информацию и привести к ее неправильной интерпретации. Так на рисунке 9.3в четко прослеживается отрицательная корреляция, а на рисунке 9.3а и 9.3б такой прослеживаемости не наблюдается. Причина состоит в том, что на рисунке 9.3а сжата ось X, а на рисунке 9.3б – ось Y.

Рисунок 9.3 – Примеры выбора разной размерности осей Х и Y
В некоторых случаях большую пользу дает расслоение данных диаграммы рассеивания на отдельные слои по какому-либо признаку.
На рисунке 9.4а представлена диаграмма рассеивания зависимости вязкости жидкости от количества в ней примесей для двух компаний А и В. Видно, что корреляции нет. Но стоило разделить данные этих двух компаний на рисунке 9.4б, как корреляция сразу же проявляется.

Рисунок 9.4 – Пример расслоения данных на диаграмме рассеивания
Диапазон переменных может играть значительную роль. На рисунке 9.5 показан случай нелинейной корреляции между X и Y.

Рисунок 9.5 – Пример нелинейной корреляции
Если же взять диапазон X < X1, то на лицо положительная линейная корреляция. При Х > Х1 отрицательная линейная корреляция. Поэтому крайне опасно экстраполировать полученные выводы за пределы полученных экспериментальных данных.
В некоторых случаях возможно наличие сильной корреляции между переменными, которые вовсе не связаны причинно-следственной связью. Корреляции такого рода называют ложными. Например, в одном исследовании была установлена сильная положительная корреляция между индексом потребительских цен и числом пожаров.
Проверка гипотезы о независимости двух признаков
При решении практических задач часто необходимо выяснить существенно ли отличается от нуля эмпирический коэффициент корреляции rxy. Иными словами взята ли выборка объемом n из двумерной нормально распределенной генеральной совокупности с коэффициентом корреляции ρxy=0, что позволяет сделать вывод о независимости случайных величин X и Y.
Таким образом, речь идет о проверке статистической гипотезы H0: ρxy=0. Опровержение этой гипотезы означает, что между X и Y существует линейная зависимость.
Для проверки этой гипотезы используют выборочную характеристику
 .
(9.8)
.
(9.8)
Методами теории вероятности показано, что эта характеристики при условии гипотезы H0 удовлетворяют распределению Стьюдента с m=n ‑ 2 степенями свободы.
Таким образом,
необходимо задаться уровнем значимости
α
и по таблице найти критическое значение
tα,m.
Тогда при
![]() гипотезаH0
должна быть
отвергнута,
что означает существенное отличие
коэффициента корреляции от нуля. Таким
образом, ρxy
≠0, а X
и Y
не являются независимыми.
гипотезаH0
должна быть
отвергнута,
что означает существенное отличие
коэффициента корреляции от нуля. Таким
образом, ρxy
≠0, а X
и Y
не являются независимыми.
Пример. На токарном станке изготовлено 150 гильз, у которых контролируется диаметр в двух взаимно перпендикулярных направлениях X и Y. В результате обработки этих данных получен коэффициент корреляции rxy=0,5273. Зависят ли друг от друга диаметры X и Y, т.е. H0: ρxy=0?
Вычисление по формуле (9.8) дает:
![]() .
.
Принимая α=0,01 получаем из таблицы приложения Е:
![]() ,
,
что означает
![]() .
Таким образом, гипотеза H0
должна быть отвергнута, то есть ρxy
≠0.
.
Таким образом, гипотеза H0
должна быть отвергнута, то есть ρxy
≠0.
Регрессионный анализ
Рассмотрим диаграмму рассеивания, построенную по результатам n пар наблюдений признаков X и Y (x1,у1), (х2,у2),...,(хn,уn), представленную на рисунке 9.6.
При рассмотрении этой диаграммы ясно видно, что между результатами измерений xi и yi обоих признаков X и Y отсутствует функциональная связь. Для всякого фиксированного значения xi случайной величины Х случайная величина Y в общем, виде принимает различные значения yi1, yi2 и т.д. Дело в том, что помимо Х на неё воздействует еще целый ряд неподконтрольных факторов. В таком случае говорят о корреляционной связи или о корреляционной (стохастической) зависимости между X и Y. Изучение и оценка этой связи с помощью математико-статистических методов входит в задачу теории регрессии.

Рисунок 9.6 – Диаграмма рассеивания признаков Х и Y
Будем говорить только о линейной регрессии для линейной корреляционной зависимости между Y и X. Возьмем X в качестве независимой, а Y зависимой случайной переменной (разумеется, можно их расставить и наоборот).
Предполагается, что для произвольного фиксированного значения X величина Y распределена в генеральной совокупности нормально с математическим ожиданием
![]() (9.9)
(9.9)
и дисперсией 2, независимой от X. Соотношение (9.9) показывает, что случайная величина Y в среднем линейно зависит от фиксированного значения X. Значения a, b и 2 в общем случае неизвестные параметры генеральной совокупности. Их необходимо определить по выборке объема n значений (x1,у1), (х2, у2), . . ., (хn, уn). Для этого пары значений (xi, yi) (i = 1, 2, ..., n) представляют в виде точек в декартовой системе координат, и делается попытка провести прямую возможно ближе к «множеству точек».
Для прямой составляется общее уравнение:
![]() .
(9.10)
.
(9.10)
Оценки неизвестных коэффициентов a и b определяются методом наименьших квадратов; исходя из требования:
![]() .
(9.11)
.
(9.11)
Выражение (9.11) требует, чтобы в точках xi вертикальное расстояние между точками измерений (xi ,yi) и соответствующими точками на искомой прямой было возможно меньше.
Возьмем частные
производные выражения (9.11) по a
и b
и приравняем их к нулю. Получим при этом
уравнение для определения оценок
параметров a
и b
в формуле (9.10). Обозначим эти оценки
через
![]() и
и![]() :
:

откуда:
![]() ,
,
т.е.:
![]() .
(9.12)
.
(9.12)
Далее:

Откуда:
![]()
и
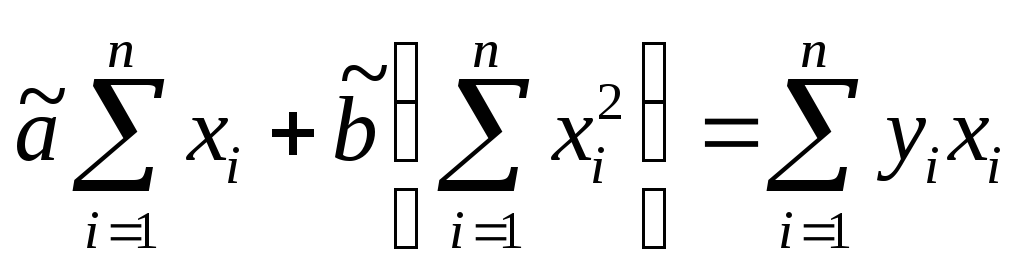 .
(9.13)
.
(9.13)
Напомним, что:
![]() ,
,
![]() .
.
Выражение (9.12) можно поэтому переписать следующим образом:
![]() ,
,
и
![]() .
(9.14)
.
(9.14)
Подставим (9.14) в (9.13):
![]()
Откуда:
![]()
и
 ,
,
и окончательно:
 .
(9.15)
.
(9.15)
Докажем окончательный вид числителя в выражении (9.15):
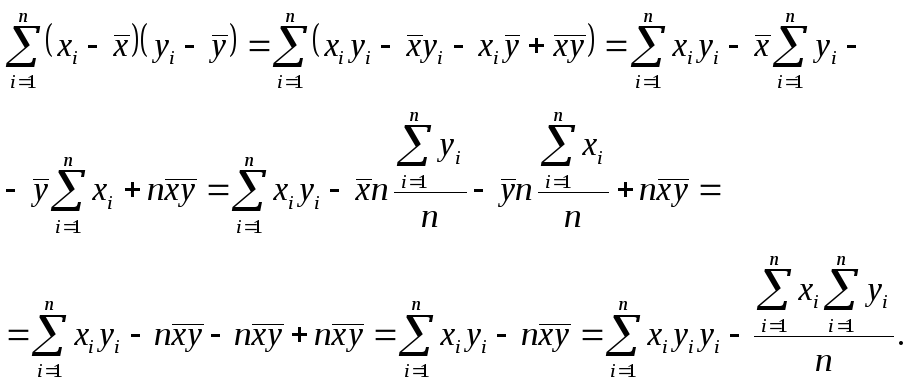
Аналогично можно показать, что окончательное выражение для знаменателя в выражении (9.15) эквивалентно первоначальному:
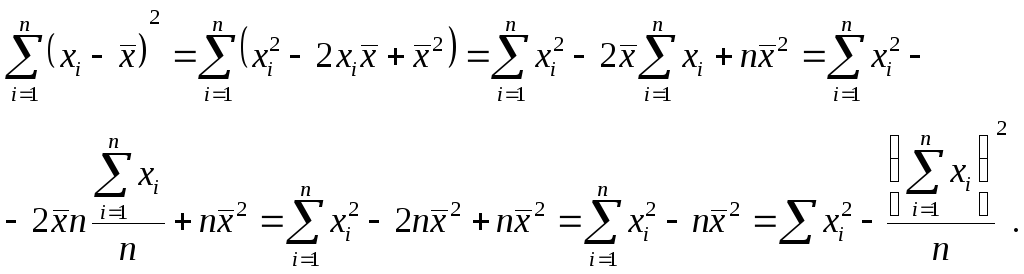
Окончательно выражение (9.15) можно записать следующим образом:
![]()
![]() ,
(9.16)
,
(9.16)
где
![]() – эмпирическая ковариация ряда измерений;
– эмпирическая ковариация ряда измерений;
![]() и
и
![]() – эмпирические дисперсии.
– эмпирические дисперсии.

С учетом формулы (9.14) получаем уравнение линейной регрессии:
![]() .
(9.17)
.
(9.17)
Коэффициент
![]() называют константой (свободным членом),
а
называют константой (свободным членом),
а![]() коэффициентом
регрессии (угловым коэффициентом).
коэффициентом
регрессии (угловым коэффициентом).
Если рассматривать характер изменения X по Y, т.е. считать, что X зависит от значения признака Y, то линия регрессии будет иметь вид:
![]() ,
(9.18)
,
(9.18)
где
 .
(9.19)
.
(9.19)
Оба уравнения
регрессии неэквивалентны, так как в
общем случае
![]() .
.
Прежде, чем проводить регрессионный анализ, необходимо сначала построить диаграмму рассеивания. Иначе можно легко допустить ошибку, не заметив этого. Ниже, на рисунке 9.7 приведены данные четырех различных испытаний, которые дают примерно одинаковую линию регрессии.
Однако точки на графиках расположены совершенно по-разному. Очевидно, что только для случая а) линия регрессии правильно отражает результат. В случае б) имеется явная нелинейная корреляция и линия регрессии должна быть кривой высшего порядка. В случае в) имеется явно выпадающий результат. Его надо либо не учитывать, либо провести дополнительные замеры в этом диапазоне. Для случая г) явно не хватает промежуточных данных, т.к. самая правая точка имеет подавляющее влияние на уравнение линии регрессии.
Контрольные вопросы
Что означает наличие функциональной связи между двумя признаками качества Х и Y?
Что означает наличие статистической связи между двумя признаками качества Х и Y?

Рисунок 9.7 – Результаты различных испытаний
с одинаковой линией регрессии
Приведите примеры двух измеряемых параметров, из которых один является характеристикой качества, а другой влияющим на нее фактором.
Приведите примеры двух измеряемых параметров, из которых оба является характеристиками качества.
Приведите примеры двух измеряемых параметров, из которых оба являются факторами, влияющими на характеристику качества.
Что такое диаграмма рассеивания?
Какие рекомендации следует соблюдать при построении диаграммы рассеивания?
Как выглядит диаграмма рассеивания с сильной положительной корреляцией?
Как выглядит диаграмма рассеивания со слабой положительной корреляцией?
Как выглядит диаграмма рассеивания с сильной отрицательной корреляцией?
Как выглядит диаграмма рассеивания со слабой отрицательной корреляцией?
Как выглядит диаграмма рассеивания при отсутствии корреляции между двумя признаками?
Покажите пример диаграммы рассеивания с нелинейной корреляцией.
Что такое корреляционная таблица?
Какие численные характеристики дают информацию о тесноте связи между двумя измеряемыми признаками?
Что такое ковариация?
Что такое коэффициент корреляции?
Какие значения может принимать коэффициент корреляции?
Охарактеризуйте силу связи между двумя измеряемыми признаками, если коэффициент корреляции оказался равным 0,4.
Охарактеризуйте силу связи между двумя измеряемыми признаками, если коэффициент корреляции оказался равным 0,6.
Охарактеризуйте силу связи между двумя измеряемыми признаками, если коэффициент корреляции оказался равным 0,85.
Что такое корреляционный анализ?
К чему может привести плохой выбор размерностей координатных осей диаграммы рассеивания?
Чем может быть полезной процедура расслоения данных на диаграмме рассеивания?
Что означает понятие «ложная корреляция»? Придумайте примеры «ложной корреляции».
Как осуществляется проверка гипотезы о независимости двух признаков?
Что такое регрессионный анализ?
Запишите уравнение линейной регрессии изменения параметра Y по параметру X.
Запишите уравнение линейной регрессии изменения параметра X по параметру Y.
Что такое коэффициент регрессии?
Какой метод положен в основу вывода формулы линейной регрессии?
Почему проведению регрессионного анализа должно предшествовать построение диаграммы рассеивания и ее изучение?
Приемочный статистический контроль
качества продукции
Общие положения
В любом производственном процессе, помимо задач применения статистических методов управления и регулирования технологических процессов, возникает задача организации приемочного контроля качества изготовленной продукции.
Целью контроля качества является отбраковка из поставленной на контроль партии продукции дефектных изделий. Это обеспечит поставку потребителю продукции заданного уровня качества, независимо от того, насколько управляем технологический процесс. Приемочный контроль находит применение при осуществлении входного, промежуточного или окончательного контроля качества.
Контроль качества продукции может быть либо сплошным, когда контролируется каждая единица продукции в партии, либо выборочным (статистическим), когда контролируется лишь часть продукции – так называемая выборка.
Сплошной контроль рекомендуется в тех случаях, когда он технически возможен и экономически целесообразен (партия продукции невелика, качество продукции в процессе контроля не ухудшается). Кроме того сплошной контроль необходим в случае возможности наличия критических несоответствий, полностью исключающих использование продукции по назначению из-за угрозы возникновения аварийных ситуаций и техногенных катастроф с непредсказуемыми последствиями для жизни, здоровья людей и окружающей среды.
Выборочный контроль обычно проводится в тех случаях, когда в процессе контроля продукция может разрушаться или изменять свои параметры, когда сплошной контроль невыгоден экономически (высокая стоимость контроля) или неосуществим технически. Во многих случаях выборочный контроль оказывается более целесообразным и экономичным, чем сплошной, особенно в условиях массового и крупносерийного производства.
При выборочном контроле решение о качестве предъявляемой на контроль партии продукции принимается по результатам проверки одной или нескольких выборок, извлеченных из этой партии.
Выборочный контроль качества продукции может осуществляться как по количественному, так и по альтернативному признаку. Выборочный контроль по количественному признаку обладает рядом преимуществ. Так, контроль по количественному признаку позволяет получить больше информации о негативном влиянии среднего процесса, его изменчивости или того и другого на качество продукции. Благодаря большей информативности при контроле по количественному признаку для обеспечения заданной степени защиты от ошибочных решений необходим меньший объем выборки. Уменьшение количества контролируемых изделий может дать экономическую выгоду, особенно в случае разрушающего или дорогостоящего контроля. Контроль по количественному признаку дает информацию не только о нахождении контролируемого параметра в определенных пределах, но и о его действительном значении, тем самым, позволяя производить оценку стабильности и воспроизводимости процесса изготовления изделий и своевременно обнаруживать его разладку.
В то же время выборочный контроль по альтернативному признаку в общем случае более прост в организации и предъявляет меньшие требования к оборудованию и квалификации персонала.
Выборочный приемочный контроль качества продукции – это, по существу, выборочный контроль, при котором по результатам проверки качества единиц продукции, входящих в случайную представительную выборку, с помощью методов математической статистики делается обоснованное заключение о качестве всей изготовленной партии продукции, о ее пригодности к поставке и использованию по назначению.
Выборочный приемочный контроль может осуществляться в следующих случаях:
изготовителем (поставщиком) при операционном контроле на различных этапах производственного процесса с целью своевременного выявления и предотвращения пропуска несоответствующей продукции на следующие производственные операции и сокращения производственных потерь, обусловленных поздним обнаружением несоответствий;
изготовителем при окончательном контроле и приемке или сертификации готовой продукции;
потребителем продукции при входном, инспекционном или эксплуатационном контроле, приемке и сертификации продукции;
третьей (независимой от поставщика и потребителя) стороной при сертификации продукции, инспекции и надзоре за соблюдением требований стандартов, контроле качества продукции, выполняемом при судебном или арбитражном рассмотрении дел.
Процедура выборочного контроля состоит из трех последовательных этапов:
извлечение выборки из партии, представленной на контроль;
проверки параметров качества изделий в выборке;
принятие решения о качестве представленной партии продукции.
При принятии решения при этом используют систему правил, именуемую планом контроля.
План и оперативная характеристика выборочного контроля
Основным инструментом выборочного контроля является план, включающий:
объем контролируемой партии продукции;
правила и порядок оформления выборок определенных объемов;
указания о виде контроля (по количественным или альтернативным признакам);
правила обработки данных контроля и принятия решений по результатам контроля выборок о соответствии или несоответствии контролируемой партии продукции установленным требованиям;
числовые характеристики условий приемки контролируемой партии.
В зависимости от количества выборок, взятых в процессе контроля, различают простые (одноступенчатые), двухступенчатые, многоступенчатые и последовательные планы контроля.
Для оценки свойств планов выборочного контроля и сравнения между собой различных планов используется оперативная характеристика. Она представляет из себя зависимость вероятности приемки контролируемой партии продукции от величины параметра, характеризующего качество этой партии продукции (например, процента брака q). Оперативная характеристика может быть выражена уравнением, таблицей или графиком.
Наиболее наглядной формой оперативной характеристики является графическая (рисунок 10.1).
Р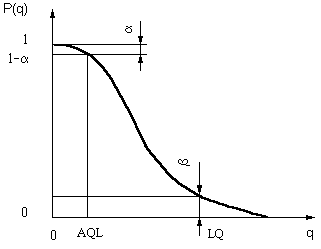 исунок
10.1 – Кривая оперативной характеристики
исунок
10.1 – Кривая оперативной характеристики
выборочного контроля
В настоящее время известны несколько подходов к организации и планированию выборочного контроля качества. Один из них – традиционный основан на концепции приемлемого уровня качества AQL (Acceptable Quality Level). Приемлемый уровень качества – это максимальный уровень несоответствий в партии продукции, который для целей приемки продукции рассматривается как удовлетворительный.
При выборочном контроле на основе AQL [10] большинство предъявляемых партий будет принято, если уровень несоответствий в этих партиях не превышает заданное значение AQL.
AQL является параметром схемы выборочного контроля и служит границей между приемлемым и неприемлемым значениями среднего уровня процесса.
При выборочном контроле из-за статистической невоспроизводимости выборки не всегда принимают безошибочное решение о контролируемой партии продукции. В силу этого существует риск забраковать партию продукции, соответствующую установленным требованиям к ее качеству. Этот риск называют риском поставщика и обозначают символом (рисунок 10.1). По существу риск поставщика – это вероятность напрасной браковки партии годной продукции.
При выборочном контроле существует также риск принять партию продукции, не соответствующую установленным требованиям к ее качеству. Этот риск называют риском потребителя и обозначают символом . По существу риск потребителя – это вероятность приемки продукции при условии ее несоответствия информации изготовителя о качестве продукции.
Риску потребителя соответствует уровень несоответствий LQ, который называют предельное допустимое качество (Limiting Quality) [11].
Выборочный контроль по альтернативному признаку
Общие положения
План контроля по альтернативному признаку включает в себя порядок отборки изделий для контроля, объем выборки, допустимое количество бракованных изделий в выборке – приемочное число с. План контроля разрабатывается на основе статистических методов.
Наибольшее распространение получили три плана контроля по альтернативным признакам:
одноступенчатые планы;
двухступенчатые планы;
планы типа последовательного анализа.
Одноступенчатые
планы. Из
партии объема N
отбирают случайным образом n
изделий (![]() ),
которые подвергаются проверке. Назначается
приемочное числос.
Если число обнаруженных дефектов в
выборке d
меньше или равно с
(
),
которые подвергаются проверке. Назначается
приемочное числос.
Если число обнаруженных дефектов в
выборке d
меньше или равно с
(![]() ),
то партия принимается. Если жеd
> с,
то партия бракуется.
),
то партия принимается. Если жеd
> с,
то партия бракуется.
Планы типа двукратной (многократной) выборки. Применение двухступенчатых планов позволяет снизить по сравнению с одноступенчатым планом среднее число проконтролированных изделий. Это представляется важным при разрушающем контроле и в случае высокой стоимости контроля каждого изделия.
В
случае применения двухступенчатого
плана контроля из партии объемом N
берут сначала выборку объемом n1.
Если в
выборке несоответствующих изделий не
более с1,
т.е.
![]() ,
то партию принимают, а если число
несоответствующих изделий
,
то партию принимают, а если число
несоответствующих изделий![]() ,
то партию бракуют. Если же число
несоответствующих изделий находится
в пределах
,
то партию бракуют. Если же число
несоответствующих изделий находится
в пределах![]() ,
то берут вторую выборку объемомn2,
и партию принимают, если общее число
несоответствующих изделий в обеих
выборках
,
то берут вторую выборку объемомn2,
и партию принимают, если общее число
несоответствующих изделий в обеих
выборках
![]() ,
и бракуют, если
,
и бракуют, если![]() .
Обычно
.
Обычно
![]() .
.
Планы типа
последовательного анализа. При
использовании этих планов задаются
объемы последовательных выборок
![]() (i
= 1, 2, …, k),
причем;
(i
= 1, 2, …, k),
причем;
![]() ;
;![]() ;
…,
;
…,![]() .
Кроме того, для каждой последовательной
выборки задаются пары целых чисел
.
Кроме того, для каждой последовательной
выборки задаются пары целых чисел![]() и
и![]() .
Вначале контроля берется выборка объема
.
Вначале контроля берется выборка объема![]() .
Если
.
Если![]() ,то
партия принимается, если
,то
партия принимается, если![]()
бракуется, если же
бракуется, если же
![]() ,
то берется выборка объема
,
то берется выборка объема![]() .
.
На i-том
шаге, если
![]() ,
то партия принимается, если
,
то партия принимается, если![]()
бракуется, если
бракуется, если
![]() ,
то берется выборка объемом
,
то берется выборка объемом![]() и т.д.
и т.д.
Каждый из указанных типов планов обладают рядом преимуществ и недостатков. С организационной точки зрения планы типа однократной выборки значительно проще. Здесь к тому же известен заранее объем выборки.
В планах типах двукратной выборки и последовательного анализа можно при том же среднем объеме выборки получить большую достоверность соответствия принимаемых решений с истинным положением дела. Однако здесь может встретиться случай, когда общий объем выборок будет чрезмерно велик. Процедуры оценки по этим планам значительно сложнее.
Построение оперативных характеристик
для планов контроля по альтернативным признакам
Одноступенчатые планы. Исходя из изложенного в пункте 10.3.1, одноступенчатый план контроля полностью задается следующими параметрами: N – объемом контролируемой партии; n ‑ объемом выборки; с – приемочным числом. Рассмотрим алгоритмы вычисления оперативной характеристики.
Пусть на контроль
поступает партия продукции объемом N
изделий, в которой D
изделий имеют дефекты. Доля дефектных
изделий q
=
![]() .
Для одноступенчатого плана оперативная
характеристика запишется следующим
образом:
.
Для одноступенчатого плана оперативная
характеристика запишется следующим
образом:
![]() ,
(10.1)
,
(10.1)
где d – число дефектных изделий в выборке объемом n;
![]() –вероятность
появления d
дефектных изделий в выборке объемом n.
–вероятность
появления d
дефектных изделий в выборке объемом n.
При статистическом контроле качества продукции используют случайную бесповторную выборку, что требует для подсчета вероятности использовать гипергеометрическое распределение. Для этого распределения вероятность того, что в выборке окажется ровно d бракованных изделий запишется формулой:
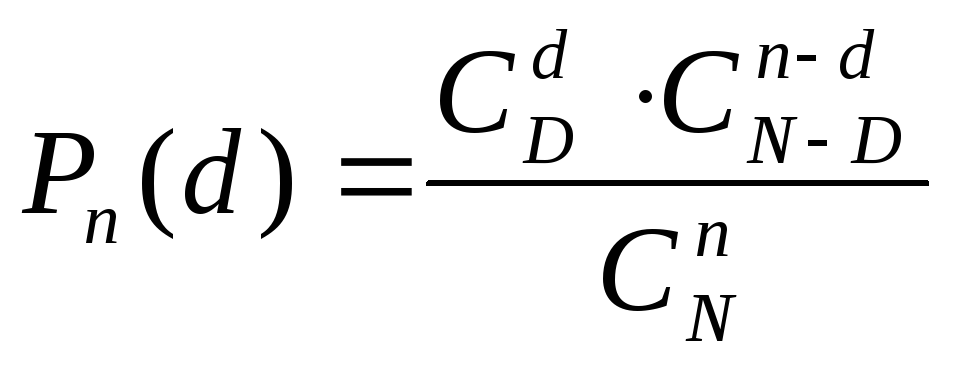 ,
(10.2)
,
(10.2)
где
![]()
число сочетаний n
элементов из N.
число сочетаний n
элементов из N.
При больших значениях N вычисление P(d) затруднительно из-за вычисления биноминальных коэффициентов (сочетаний).
В случае если из контролируемой партии с уровнем несоответствий изделий q берут выборку с возвращением объемом n, то случайная величина d имеет биномиальное распределение.
Хотя взятие выборок с возвращением в практике выборочного контроля не встречается, биномиальное распределение обычно используют в качестве аппроксимации более сложного для расчетов оперативной характеристики гипергеометрического распределения. Такая аппроксимация применима (дает малую погрешность), если выборка составляет малую часть объема контролируемой партии (n<0,1N).
Для биномиального распределения вероятность того, что в выборке имеется d несоответствующих изделий, определяется следующим выражением:
![]() ,
(10.3)
,
(10.3)
где
![]() – вероятность появления годного изделия.
– вероятность появления годного изделия.
Вероятность того, что в выборке объемом n будет не более с несоответствующих изделий, определяется следующим выражением:
![]() .
(10.4)
.
(10.4)
Это
соотношение позволяет производить
расчет оперативной характеристики
одноступенчатого плана контроля с
параметрами N,
n
и с.
Для этого рассчитываем значение
![]() ,
т.е. вероятность приемки партии продукции,
для различных значений уровня
несоответствующих изделий в контролируемой
партии (q
= M/N).
,
т.е. вероятность приемки партии продукции,
для различных значений уровня
несоответствующих изделий в контролируемой
партии (q
= M/N).
Для
расчета значений
![]() можно использовать табличные значения
кумулятивных биномиальных вероятностей,
представленные в приложении А. При этом
надо учитывать, что:
можно использовать табличные значения
кумулятивных биномиальных вероятностей,
представленные в приложении А. При этом
надо учитывать, что:
![]() .
(10.5)
.
(10.5)
Если помимо этого доля дефектных изделий меньше 10% (q<0,1), то хорошим приближением к биноминальному распределению является пуассоновское:
![]()
![]() .
(10.6)
.
(10.6)
Это распределение
применимо и для небольших значений n,
когда
![]() достаточно
мало. Здесь
достаточно
мало. Здесь![]()
математическое ожидание числа дефектов
в выборке объемом n.
Вероятность принятия партии будет равна
сумме вероятностей попадания в выборке
0, 1, 2, …, с
дефектных изделий:
математическое ожидание числа дефектов
в выборке объемом n.
Вероятность принятия партии будет равна
сумме вероятностей попадания в выборке
0, 1, 2, …, с
дефектных изделий:
![]() .
(10.7)
.
(10.7)
Пример 10.1. Вычислить и построить оперативную характеристику для плана контроля при n=100, с=4, используя биномиальное распределение.
Решение. Вероятность принять партию для q=0 равна единице (100%). Находим, используя приложение А и уравнение (10.5) вероятности приемки партии для доли брака 0,02; 0,05 и 0,08:
 ;
;
 .
.
По полученным точкам строим оперативную характеристику (рисунок 10.2).

Рисунок 10.2 Расчетная оперативная характеристика
Двухступенчатые планы. Исходя из изложенного в п. 10.3.1 двухступенчатый план контроля полностью задается следующими параметрами:
N – объемом контролируемой партии;
 –приемочным
числом на первой ступени контроля;
–приемочным
числом на первой ступени контроля;  –браковочным
числом на первой ступени контроля;
–браковочным
числом на первой ступени контроля;  –приемочным
числом на второй ступени контроля;
–приемочным
числом на второй ступени контроля;  –браковочным
числом на второй ступени контроля;
–браковочным
числом на второй ступени контроля; n1 и n2 – объемом выборки на первой и второй ступенях контроля.
При
этом параметры плана контроля n1,
![]() ,
,![]() и
и![]() должны отвечать следующим ограничениям:
должны отвечать следующим ограничениям:
![]() .
(10.8)
.
(10.8)
При реализации двухступенчатого плана контроля возможны четыре различных исхода. Вероятность каждого из них зависит от уровня несоответствующих изделий в контролируемой партии q и равна:
 –вероятность
приемки партии на основании результатов
контроля первой выборки;
–вероятность
приемки партии на основании результатов
контроля первой выборки; –вероятность
браковки партии на основании результатов
контроля первой выборки;
–вероятность
браковки партии на основании результатов
контроля первой выборки; 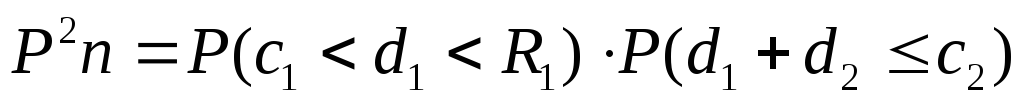 –вероятность
приемки партии на основании результатов
контроля второй выборки;
–вероятность
приемки партии на основании результатов
контроля второй выборки;  –вероятность
браковки партии на основании результатов
контроля второй выборки.
–вероятность
браковки партии на основании результатов
контроля второй выборки.
Вероятность того, что партия при заданном уровне несоответствий q будет принята после контроля первой или второй выборки, определяется следующим соотношением:
![]() .
(10.9)
.
(10.9)
Это выражение позволяет производить расчет оперативной характеристики двухступенчатого плана контроля качества. Расчет значений вероятностей, стоящих в его правой части, производится с помощью соотношений (10.4), (10.5) и таблицы кумулятивных биномиальных вероятностей в приложении А.
Значение
сомножителя
![]() в выражении (10.9) вычисляется по следующей
формуле:
в выражении (10.9) вычисляется по следующей
формуле:
![]() .
(10.10)
.
(10.10)
Свойства оперативной характеристики. Посмотрим, как будет вести себя приемочная кривая при постоянном объеме выборки n и изменении приемочного числа с. Если в рассмотренном ранее примере 10.1 взять с=5, то при одном и том же проценте брака вероятность принятия партии будет увеличена. Действительно к вероятности принять в выборке не более четырех бракованных деталей добавится вероятность принять пятую деталей. Таким образом, кривая для с=5 лежит правее кривой для с=4 и т.д. Общая закономерность изменения вида оперативной характеристики при изменении приемочного числа показана на рисунке 10.3.
Теперь посмотрим, как изменится оперативная характеристика с увеличением объема выборки при постоянном приемочном числе с. Пусть с=4, а n=200. По сравнению с с=4 и n=100 в выборку большего объема попадает большее число дефектных изделий. Следовательно, чем больше при постоянном значении q и c объем выборки, тем чаще число бракованных изделий в ней будет превышать приемочное число, тем меньше будет вероятность принять партию. Семейство оперативных характеристик при постоянном приемочном числе (с=4) и разных объемах выборки показано на рисунке 10.4.

Рисунок 10.3 Семейство оперативных характеристик для n=100

Рисунок 10.4 Семейство оперативных характеристик для с=4
Все оперативные
характеристики выборочных планов с
отличным от нуля приемочным числом (![]() )
имеют точку перегиба, абсцисса которой
равна
)
имеют точку перегиба, абсцисса которой
равна![]() при использовании распределения Пуассона
(рисунок 10.5) и
при использовании распределения Пуассона
(рисунок 10.5) и![]() при использовании биноминального
распределения. В этом легко убедиться,
если соответствующее уравнение, например,
(10.4) или (10.5) дважды продифференцировать
поq.
при использовании биноминального
распределения. В этом легко убедиться,
если соответствующее уравнение, например,
(10.4) или (10.5) дважды продифференцировать
поq.
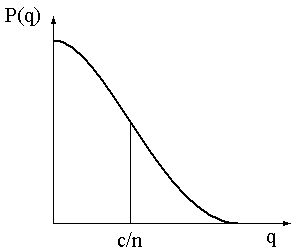
Рисунок 10.5 Точка перегиба на оперативной характеристике
Стандартные методы выборочного контроля
по альтернативному признаку
В настоящее время обосновано множество методов и разработано огромное количество таблиц для планирования и оценки результатов выборочного контроля по альтернативному признаку. Эти методы и таблицы систематизированы в национальных стандартах. Можно назвать такие стандарты как:
британский – BS 6001;
немецкий – TGL 14450
российские – ГОСТ Р 50779.71-99 и т. п.
Эти методы и таблицы имеют широкие возможности. Так в обзорной части ГОСТ Р 50779.71-99 «Процедуры выборочного контроля по альтернативному признаку» сказано, что выборочные планы распространяются на контроль следующих объектов:
готовой продукции;
комплектующих и сырья;
операций;
материалов в процессе производства;
поставок на складе;
операций обслуживания;
данных и записей;
административных процедур.
Наибольшее распространение в мире получила выборочная система AQL, т. е. программы выборки на основе риска производителя.
Кроме этого используют следующие системы:
система LQ, использующая программы выборки на основе риска потребителя;
система Dmax – максимально среднего уровня выходного качества и др.
Рассмотрим процедуры выборочного контроля последовательных партий на основе приемлемого уровня качества (AQL) по ГОСТ Р 50779.71-99.
В стандарте устанавливаются правила проведения контроля и оценки его результатов по представленным планам и схемам контроля. Основой для выбора планов и схем контроля являются AQL и код объема выборки. Назначение AQL означает, что выборочная схема будет принимать большинство предъявленных партий, если уровень несоответствий в них не превышает заданное значение AQL. AQL оговаривается в контракте. Таблицы в стандарте содержат предпочтительные значения AQL: 0,01; 0,015; ...; 0,10; ...; 1,0; ...; 10; 15; …, 100; …; 1000.
Значения AQL до 10 устанавливают как для процента несоответствующих единиц продукции, так и для числа несоответствия на 100 единиц продукции. Значения AQL более 10 устанавливаются только для числа несоответствий на 100 единиц продукции.
Код объема выборки зависит от назначенного уровня контроля и объема выборки. На рисунке 10.6, в качестве примера, представлен фрагмент таблицы кодов объема выборки ГОСТа Р 50779.71-99.
Если нет других предписаний, пользуются общим уровнем 2. Для менее четкого отбора хороших и плохих партий применяем уровень 1, при более четком уровень 3.
Специальные уровни могут быть назначены при относительно небольших объемах выборки и больших рисках связанных с выборкой. Их используют при разрушающем или очень дорогостоящем контроле. Персонал при этом должен быть компетентен.
Стандартом предусмотрены разные виды контроля: нормальный, усиленный и ослабленный. На начальном этапе должен быть установлен нормальный контроль (если не предусмотрено ничего другого). Назначенный вид контроля продолжают до тех пор, пока не возникает необходимость выполнить переключение. Процедуры и правила переключения рассмотрены на рисунке 10.7.
|
Объем партии |
Код объема выборки при уровне контроля | ||||||
|
Специальные |
Общие | ||||||
|
S-1 |
S-2 |
S-3 |
S-4 |
1 |
2 |
3 | |
|
от 2 до 8 |
A |
A |
A |
A |
A |
A |
B |
|
9 - 15 |
A |
A |
A |
A |
A |
B |
A |
|
16 -25 |
A |
A |
B |
B |
B |
C |
D |
|
.............. |
… |
… |
… |
… |
… |
… |
… |
|
281-500 |
B |
C |
D |
E |
F |
H |
J |
|
.............. |
… |
… |
… |
… |
… |
… |
… |
|
35001-150000 |
D |
E |
G |
J |
L |
N |
P |
|
св. 500000 |
D |
E |
H |
K |
N |
Q |
R |
Рисунок 10.6 – Фрагмент таблицы выбора кодов объема выборки из ГОСТ Р 50779.71-99

Рисунок 10.7 Процедуры и правила переключения
Типы планов выборочного контроля.
В ГОСТе предположены три типа выборочных планов – одно, двух – и многоступенчатые. При наличии нескольких типов планов для данной AQL и кода объема выборки можно использовать любой из них.
Решение о выборе типа плана базируется на сравнении организационных проблем и средних объемов выборок. Закономерности здесь следующие:
Средний объем выборки для многоступенчатого типа контроля меньше, чем для двухступенчатого, а для последнего, в свою очередь, меньше, чем для одноступенчатого (рисунок 10.8).
В то же время для одноступенчатого контроля характерны меньшие затраты и меньшие организационные проблемы.
В стандарте представлены таблицы одноступенчатых, двухступенчатых и многоступенчатых планов при нормальном, ослабленном и усиленном контроле. В таблицах выборочных планов для каждого кода выборки даны объемы выборки, рекомендованные значения AQL, для каждого из которых приведены два числа – приемочное (АС) и бракованное (RC). Фрагмент таблицы одноступенчатого плана при нормальном контроле представлен на рисунке 10.9.
Стандарт в качестве предпочтительных планов рекомендует использовать первые планы под стрелкой и над стрелкой.

с – приемочное число для первой выборки; 2 – двухступенчатый план; 1 – многоступенчатый; n – объем выборки эквивалентного одноступенчатого плана.
Рисунок 10.8 – Сравнение объемов выборки для
различных типов планов контроля
|
Код объема выборки |
Объем выборки |
Значение AQL | |||||
|
0,010 |
0,015 |
0,025 |
0,040 |
0,065 |
0,10 | ||
|
A B C |
2 3 5 |
01 |
|
|
|
|
|
|
D E F |
8 13 20 | ||||||
|
G H J |
32 50 80 | ||||||
|
1K L
M |
125 200
315 |
0 1 | |||||
|
0 1 |
| ||||||
|
0 1 |
|
| |||||
|
N
P
Q |
500
800
1250 |
0 1 |
|
|
1 2 | ||
|
0 |
|
|
1 2 |
2 3 | |||
|
|
|
1 2 |
2 3 |
3 4 | |||
|
R |
2000 |
|
1 2 |
2 3 |
3 4 |
5 6 | |
Рисунок 10.9 – Фрагмент таблицы № II-A одноступенчатого плана при нормальном контроле из ГОСТ Р 50779.71-99
Выборочный контроль по количественному признаку
Особенности выборочного контроля
по количественному признаку
Необходимым условием эффективного использования выборочного контроля по количественному признаку является знание закона распределения контролируемого параметра. Как правило, полагают, что контролируемый параметр имеет точно или приближенно нормальное распределение. Если реальное распределение не является нормальным, то контроль по количественному признаку может привести как к ошибочной браковке партии практически годной продукции, так и, наоборот, к приемке партий бракованной продукции. Поэтому при проведении выборочного контроля по количественному признаку целесообразно осуществлять проверку согласия опытного распределения контролируемого параметра с нормальным законом.
Теоретическое обоснование методов выборочного контроля по количественному признаку проводится для случая одновременного выполнения следующих условий:
контроль проводят по одному количественно измеряемому показателю качества изделий;
для измеряемого при контроле показателя качества установлены нижнее L или верхнее U предельное значение показателя или оба предельных значения (границы поля допуска);
для контролируемого показателя качества и установленных предельных значений задан критерий качества в виде, например, приемлемого уровня качества AQL;
процедуру контроля применяют для непрерывной последовательности партий дискретных изделий, поставляемых одним изготовителем, который использует единый производственный процесс;
производство стабильно и значение показателя качества изделий распределено по нормальному закону распределения;
стандартное отклонение известно, если оно неизвестно, то можно использовать его оценку, полученную по выборочным данным.
математическое ожидание распределения измеряемого показателя качества , характеризующее уровень настройки производственного процесса, рассматривается как переменная величина.
Оперативные характеристики
одноступенчатых планов выборочного контроля
по количественному признаку
При проведении выборочного контроля по количественному признаку качество контролируемой партии изделий принято характеризовать как уровнем настройки процесса, т.е. в виде требования к среднему значению контролируемого параметра, так и требованием к уровню несоответствующей продукции. Поэтому в качестве аргумента оперативной характеристики плана выборочного контроля по количественному признаку используют уровень несоответствий в контролируемой партии продукции q, либо среднее значение контролируемого параметра .
При использовании концепции приемлемого уровня качества AQL выражения для расчета оперативных характеристик одноступенчатого плана выборочного контроля при известной дисперсии имеют следующий вид:
при задании уровня несоответствий q:
![]() ;
(10.11)
;
(10.11)
при задании нижнего предельного значения контролируемого параметра L
![]() ;
(10.12)
;
(10.12)
при задании верхнего предельного отклонения контролируемого параметра U
![]() ,
(10.13)
,
(10.13)
где
![]() ,
(10.14)
,
(10.14)
 ,
(10.15)
,
(10.15)
где
![]() ,
,![]() ,
,![]() ,
,![]() квантили нормального закона распределения
уровня,
,
AQL, LQ соответственно (таблица в
приложении К);
квантили нормального закона распределения
уровня,
,
AQL, LQ соответственно (таблица в
приложении К);
n объем выборки;
и риск соответственно поставщика и потребителя.
Квантиль уровня это значение случайной величины, для которой функция распределения принимает значение .
Выборочный контроль по количественному признаку
согласно стандарту ГОСТ Р 50779.74-99
Планы и процедуры выборочного контроля по количественному признаку на основе объема партии приемлемого уровня качества AQL и уровней контроля установлены в ГОСТ Р 50779.74-99 [12].
Этот стандарт применим для случаев, когда выполняются следующие условия:
процедура контроля предназначена для непрерывной последовательности партий дискретной продукции, поставляемой одним поставщиком, использующим один и тот же производственный процесс;
рассматривается только одна характеристика качества х этой продукции, измеряемая с помощью инструмента с непрерывной шкалой;
процесс находится в состоянии статистической управляемости и измеряемая характеристика х имеет нормальное распределение;
договором на поставку определены верхний L или нижний U предел допуска или оба предела, а продукция оценивается как несоответствующая, если измеряемая характеристика х этой продукции удовлетворяет одному из следующих неравенств:
![]() ,
(10.16)
,
(10.16)
![]() ,
(10.17)
,
(10.17)
![]() или
или
![]() .
(10.18)
.
(10.18)
Неравенства (10.16) и (10.17) соответствуют случаю одностороннего допуска, а неравенство (10.18) – двустороннего допуска. В последнем случае возможны два способа задания AQL:
для каждого предела допуска задается отдельный AQL (так называемые предельные значения с отдельными уровнями качества);
задается общий AQL для обоих пределов поля допуска (предельные значения с общим уровнем качества).
В настоящем стандарте представлены два основных метода: S‑метод для случаев, когда неизвестно стандартное отклонение контролируемой партии продукции, и -метод, если значение стандартного отклонения известно.
С точки зрения минимального объема контроля, преимущества на стороне -метода, но прежде чем его применять, необходимо установить значение . Поэтому на практике первоначально следует начать с контроля по S-методу и переход к -методу возможен только при наличии серьезных оснований считать стандартное отклонение постоянным и известным.
При контроле по S-методу объем выборки остается постоянным во всем диапазоне AQL. Исходными данными при планировании выборочного контроля являются объем партии, приемлемый уровень качества AQL, вид контроля (нормальный, усиленный или ослабленный) и уровень контроля. Причем приемлемый уровень качества и уровень контроля устанавливаются при заключении контракта и не изменяются на протяжении всего срока его действия.
В стандарте приведены три общих уровня контроля (I, II и III) и два специальных уровня (S1 и S2). Уровню I соответствует объем выборки, который несколько меньше половины объема выборки на уровне контроля II, в то время как уровню III соответствует объем выборки, в полтора раза превышающий объем выборки уровня II. Как правило, если это особенно не оговорено, применяют уровень контроля II. Специальные уровни контроля разработаны для ситуаций, когда объемы выборки должны быть малыми, что необходимо для дорогих или разрушающих испытаний.
Процедура контроля предусматривает выполнение следующих действий:
По заданному уровню контроля и объему партии с помощью таблицы 1А ГОСТ 50779.74 находят код объема выборки.
С помощью этого кода и заданного значения AQL из таблиц IIА – IIС получают объем выборки n и контрольный норматив К.
При использовании плана с двусторонним допуском определяют величину максимального выборочного стандартного отклонения MSSD по формуле:
 ,
где
,
где находят по таблицеIvs
ГОСТ 50779.74.
находят по таблицеIvs
ГОСТ 50779.74. Взяв случайную выборку объема n, измеряют показатель качества х каждой единицы продукции, после чего вычисляют среднее арифметическое выборки
 и выборочное стандартное отклонениеS.
и выборочное стандартное отклонениеS.
Если
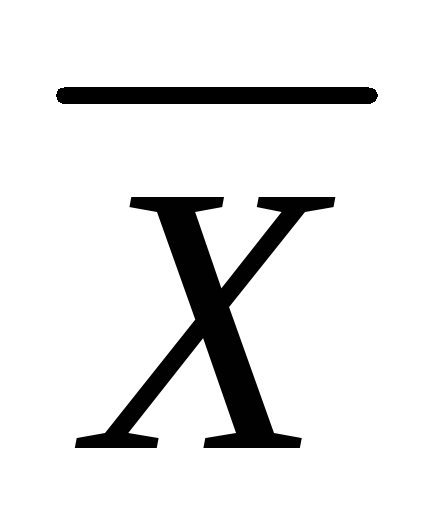 выходит за пределы поля допуска илиS
превышает значение MSSD,
то партия считается неприемлемой.
выходит за пределы поля допуска илиS
превышает значение MSSD,
то партия считается неприемлемой. Если
 не выходит за пределы поля допуска, аS
не превышает значение MSSD,
то вычисляют статистики качества по
следующим формулам:
не выходит за пределы поля допуска, аS
не превышает значение MSSD,
то вычисляют статистики качества по
следующим формулам:
![]() ,
(10.19)
,
(10.19)
или
![]() ,
(10.20)
,
(10.20)
после чего статистики
качества
![]() и (или)
и (или)![]() сравнивают с контрольным нормативомК.
Если соответствующая статистика больше
или равна К,
то партия принимается, в противном
случае она отклоняется.
сравнивают с контрольным нормативомК.
Если соответствующая статистика больше
или равна К,
то партия принимается, в противном
случае она отклоняется.
Таким образом, если указано только верхнее предельное значение поля допуска U, то партия:
принимается, если
 ;
;не принимается, если
 .
.
Если указано только нижнее значение поля допуска L, то партия:
принимается, если
 ;
;не принимается, если
 .
.
Если заданы U
и L
(значения
![]() и
и![]() различны, если даются разные AQL), то
партия:
различны, если даются разные AQL), то
партия:
принимается, если
 и
и ;
;не принимается, если выполняется хотя одно из условий:
 или
или .
.
Пример. Пиротехническая задержка по времени должна составлять от 4 до 9 секунд. Произведенная продукция контролируется партиями по 1000 изделий: уровень контроля II, нормальный контроль, AQL =0,1% для нижнего предела поля допуска и AQL=2,5% для верхнего предела.
Из таблицы IА
ГОСТ 50779.74 видно, что для такого размера
партии код равен J.
Из таблицы IВ
видно, что для S-метода
объем выборки равен 35 и по таблице IIА
находим, что верхний и нижний контрольные
нормативы составляют соответственно
![]() =1,57
и
=1,57
и![]() =2,54.
=2,54.
После измерения времени задержки для выбранных изделий и обработки полученных данных получена следующая информация:
объем выборки n=35;
среднее арифметическое выборки
 =6,55;
=6,55;стандартное отклонение S = 0,31;
верхнее предельное отклонение U=9,0;
статистика
 =7,9;
=7,9;контрольный норматив
 =1,57;
=1,57;нижнее предельное отклонение L =4,0:
статистика
 =8,23:
=8,23:контрольный норматив
 =2,54;
=2,54;критерий приемки равен:
 и
и
7,90>1,57 и 8,23>2,54
7,90>1,57 и 8,23>2,54
Таким образом, данная партия отвечает критерию приемки и может быть принята.
Контрольные вопросы
В каких случаях целесообразно применять сплошной контроль качества?
В каких случаях целесообразно применять выборочный контроль?
В чем состоят преимущества выборочного контроля по альтернативному признаку?
В чем состоят преимущества выборочного контроля по количественному признаку?
Кто и в каких случаях может производить выборочный контроль?
Из каких этапов состоит процедура выборочного контроля?
Что включает в себя план контроля?
Какие бывают планы контроля в зависимости от количества выборок?
Что такое оперативная характеристика?
Какими способами может быть выражена оперативная характеристика?
Что такое AQL и его использование при выборочном контроле?
Что такое риск производителя?
Что такое риск поставщика?
Что включает в себя план контроля по альтернативному признаку?
Охарактеризуйте одноступенчатый план контроля по альтернативному признаку.
Охарактеризуйте двухступенчатый план контроля по альтернативному признаку.
Охарактеризуйте план контроля по альтернативному признаку типа последовательного анализа.
Опишите алгоритм вычисления оперативной характеристики одноступенчатого плана контроля по альтернативному признаку с использованием гипергеометрического распределения.
Опишите алгоритм вычисления оперативной характеристики одноступенчатого плана контроля по альтернативному признаку с использованием биномиального распределения.
Опишите алгоритм вычисления оперативной характеристики одноступенчатого плана контроля по альтернативному признаку с использованием распределения Пуассона.
Опишите алгоритм вычисления оперативной характеристики двухступенчатого плана контроля по альтернативному признаку.
Докажите правильность выражения 9.5.
Докажите правильность выражения 9.10.
Как изменяется приемочная кривая плана контроля по альтернативному признаку при постоянном объеме выборки n и изменении приемочного числа с?
Как изменяется приемочная кривая плана контроля по альтернативному признаку при постоянном приемочном числе с и изменении объема выборки n?
Как найти точку перегиба приемочной кривой плана контроля по альтернативному признаку?
На контроль каких объектов распространяются процедуры выборочного контроля по ГОСТ Р 50779.71-99?
Какие выборочные системы контроля используются в мировой практике? Какая из них получила наибольшее распространение?
Что является основой выбора планов и схем контроля по ГОСТ Р 50779.71-99?
Какие предпочтительные значения AQL содержат таблицы в стандарте ГОСТ Р 50779.71-99?
Что такое код объема выборки и как он выбирается по ГОСТ Р 50779.71-99?
Какие виды контроля предусматриваются стандартом ГОСТ Р 50779.71-99?
Опишите процедуры и правила переключения между нормальным, ослабленным и усиленным видами контроля по ГОСТ Р 50779.71-99.
Назовите типы планов контроля по ГОСТ Р 50779.71-99.
На основе чего принимается решение о выборе типа плана контроля по ГОСТ Р 50779.71-99?
Как организованы таблицы выборочных планов контроля в ГОСТ Р 50779.71-99?
Какому закону должно соответствовать распределение контролируемого параметра при проведении выборочного контроля по количественному признаку?
Чем принято характеризовать качество контролируемой партии изделий при проведении выборочного контроля по количественному признаку (что выбирается в качестве аргумента оперативной характеристики плана выборочного контроля)?
Как вычисляется оперативная характеристика одноступенчатого плана выборочного контроля при задании уровня несоответствий q и использовании концепции приемлемого уровня качества AQL?
Как вычисляется оперативная характеристика одноступенчатого плана выборочного контроля при задании нижнего предельного значения контролируемого параметра L и использовании концепции приемлемого уровня качества AQL?
Как вычисляется оперативная характеристика одноступенчатого плана выборочного контроля при задании верхнего предельного отклонения контролируемого параметра U и использовании концепции приемлемого уровня качества AQL?
Что такое квантиль нормального закона распределения уровня и как он находится?
Какие условия должны выполняться для применения стандарта ГОСТ Р 50779.74-99 на планы и процедуры выборочного контроля по количественному признаку на основе объема партии приемлемого уровня качества AQL и уровней контроля?
Какие два основных метода представлены в стандарте ГОСТ Р 50779.74-99?
Что является исходными данными при планировании выборочного контроля по S – методу согласно ГОСТ Р 50779.74-99?
Какие уровни контроля предусмотрены стандартом ГОСТ Р 50779.74-99?
Опишите процедуру контроля по S – методу согласно ГОСТ Р 50779.74-99.
Задачи для самостоятельной работы
Постройте оперативные характеристики для одноступенчатого плана контроля по альтернативному признаку для следующих наборов исходных данных:
а) n =100, с1 =2, с2 =5, с3 =10;
б) с =5, n1 =50, n2 =100, n2 =200.
При построении используйте следующие уровни несоответствующих изделий (в процентах) q: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 15 и 20.
Отметьте и объясните различия между этими оперативными характеристиками.
Постройте оперативные характеристики для двухступенчатого плана контроля по альтернативному признаку при следующих исходных данных:
|
№ п/п |
n1 |
|
|
n2 |
|
|
|
1 |
20 |
1 |
3 |
20 |
3 |
4 |
|
2 |
50 |
1 |
3 |
50 |
3 |
4 |
|
3 |
100 |
1 |
3 |
100 |
3 |
4 |
|
4 |
20 |
0 |
2 |
20 |
2 |
3 |
|
5 |
50 |
0 |
2 |
50 |
2 |
3 |
|
6 |
100 |
0 |
2 |
100 |
2 |
3 |
|
7 |
100 |
0 |
3 |
100 |
3 |
4 |
|
8 |
50 |
1 |
4 |
50 |
4 |
5 |
При построении оперативных характеристик используйте следующие уровни несоответствующих изделий (в процентах) q: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 15 и 20.
Ввиду большого объема вычислений по выражению (17), все промежуточные записи для избежания ошибок целесообразно оформлять в виде таблицы. В столбцах этой таблицы располагаются значения следующих величин:
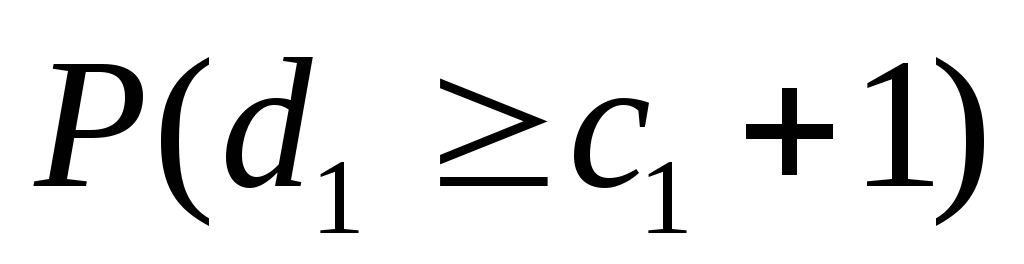 ;
; =
= ;
; ;
; ;
;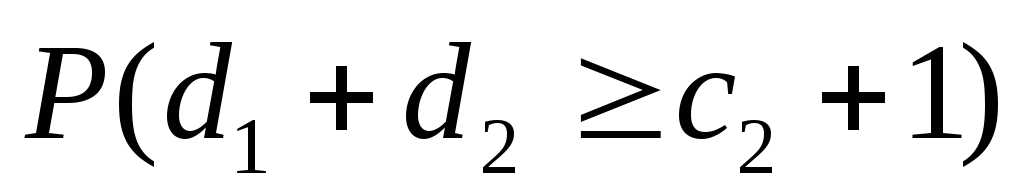 ;
;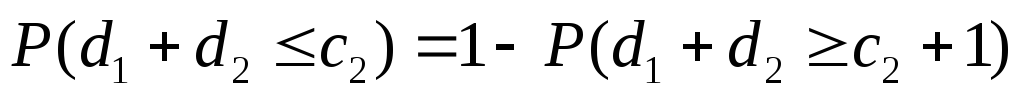 ;
; ;
; .
.
Постройте оперативные характеристики планов контроля по количественному признаку при задании уровня несоответствия для следующих исходных данных:
|
№ п/п |
|
|
AQL,% |
LQ,% |
|
1 |
0,01 |
0,05 |
1,0 |
10 |
|
2 |
0,05 |
0,05 |
6,5 |
10 |
|
3 |
0,1 |
0,05 |
6,5 |
10 |
|
4 |
0,05 |
0,01 |
1,0 |
10 |
|
5 |
0,05 |
0,01 |
4,0 |
10 |
|
6 |
0,05 |
0,01 |
1,0 |
10 |
|
7 |
0,01 |
0,01 |
2,5 |
10 |
При построении оперативных характеристик используйте следующие уровни несоответствия q (в процентах): 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 15 и 20.
Постройте оперативные характеристики планов контроля по количественному признаку при задании нижнего предельного значения контролируемого параметра L для следующих исходных данных:
|
№ п/п |
|
L |
|
|
AQL,% |
LQ,% |
|
1 |
0,34 |
59,8 |
0,01 |
0,05 |
1,0 |
10 |
|
2 |
0,34 |
60,0 |
0,01 |
0,05 |
2,5 |
10 |
|
3 |
0,3 |
89,6 |
0,1 |
0,05 |
4,0 |
10 |
|
4 |
0,45 |
149,7 |
0,05 |
0,01 |
4,0 |
10 |
|
5 |
0,5 |
193,8 |
0,05 |
0,05 |
2,5 |
10 |
При
построении оперативной характеристики
целесообразно выбрать шаг изменения
в диапазоне
(0,1…0,2)
![]() .
.
Построить оперативные характеристики при задании верхнего предельного значения контролируемого параметра U для следующих исходных данных:
|
№ п/п |
|
U |
|
|
AQL,% |
LQ,% |
|
1 |
0,34 |
59,6 |
0,05 |
0,01 |
2,5 |
10 |
|
2 |
0,41 |
119,8 |
0,1 |
0,01 |
4,0 |
10 |
|
3 |
0,45 |
149,7 |
0,05 |
0,01 |
2,5 |
10 |
|
4 |
0,41 |
79,0 |
0,01 |
0,01 |
1,0 |
10 |
|
5 |
0,5 |
193,3 |
0,1 |
0,05 |
1,0 |
10 |
При
построении оперативной характеристики
целесообразно выбрать шаг изменения
в диапазоне
(0,1…0,2)
![]() .
.
Статистическое управление процессом
при помощи контрольных карт
Общие положения
Традиционный подход к производству состоит в изготовлении продукции, контроле ее качества и отбраковке единиц, не соответствующих установленным требованиям. Такая стратегия далека от совершенства, т.к. построена на простой проверке постфактума, когда бракованная продукция уже создана.
Более эффективна стратегия предупреждения потерь, позволяющая избежать производства негодной продукции. Такая стратегия предполагает сбор информации о самих процессах, ее анализ и эффективные действия по отношению к ним, а не к продукции.
Таким образом, речь идет об управлении процессами. Но любым процессам характерна изменчивость и информация, собираемая о процессе, имеет разброс. Поэтому речь должна идти о статистической обработке информации и о статистическом управлении процессом.
Основным инструментом статистического управления качеством являются контрольные карты. Контрольные карты – это графический способ представления и сопоставления информации, основанной на последовательности выборок, отражающих текущее состояние процесса, с границами, установленными на основе изменчивости, внутренне присущей процессу.
Первоначально контрольные карты были разработаны У. Шухартом для применения в промышленном производстве. В настоящее время их широко используют в сфере обслуживания и других областях.
Теория контрольных карт различает два вида изменчивости. Первый вид – изменчивость из-за «случайных» (обычных) причин. Эти причины бесчисленны, разнообразны, присутствуют постоянно. Их нелегко, или невозможно выявить. Каждая из таких причин составляет очень малую долю общей изменчивости, и ни одна из них не значима сама по себе. Тем не менее, сумма всех этих причин существенна и предполагается, что она внутренне присуща процессу. Исключение или уменьшение влияния обычных причин требует управленческих решений и выделения ресурсов на улучшение процесса и системы в целом.
Второй вид изменчивости – реальные перемены в процессе. Они могут быть следствием некоторых определенных причин, не присущих процессу внутренне и могут быть устранены, по крайней мере, теоретически. Эти выявляемые причины рассматриваются как «неслучайные» или «особые» причины изменчивости. К ним могут быть отнесены, например, поломка инструмента, недостаточная однородность материала, отказы производственного или контрольного оборудования, недостаточная квалификация персонала, невыполнение процедур, ошибки в выполнении процедур и т.п.
Цель контрольных карт – обнаружить неестественные изменения в процессе, т.е. изменчивость второго вида и дать критерии для обнаружения отсутствия статистической управляемости.
Преимущество контрольных карт – простота их построения и применения. Они служит своевременным индикатором статистически управляемого процесса.
В тоже время контрольные карты – только часть полной системы анализа процесса. С их помощью можно предсказать момент, когда определенная причина изменит течение процесса. Но для установления природы этой причины и корректировки процесса необходимо проводить независимое исследование.
Виды контрольных карт
Существует три основных вида контрольных карт:
Контрольные карты Шухарта [14].
Приемочные контрольные карты [16].
Адаптивные контрольные карты.
С помощью контрольных карт Шухарта, как правило, оценивают только, находится ли процесс в статистически управляемом состоянии. Приемочные контрольные карты предназначены специально для определения критериев приема процесса. С помощью адаптивной контрольной карты регулируют процесс посредством планирования его тренда и проведение упреждающей корректировки на основании прогнозов.
Для каждого из этих видов применяют различные типы карт. В качестве примера приведем перечень контрольных карт Шухарта:
контрольные карты для количественных признаков:
 –карта выборочных
средних;
–карта выборочных
средних;Ме – карта медиан;
R – карта размахов;
 –карта выборочных
стандартных отклонений;
–карта выборочных
стандартных отклонений; Х– карта индивидуальных значений.
контрольные карты для альтернативных признаков:
р – карта долей несоответствующих единиц продукции;
nр – карта несоответствующих единиц продукции;
с – карта числа несоответствий;
u – карта числа несоответствий, приходящихся на единицу продукции.
Контрольные карты Шухарта
Основы контрольных карт Шухарта
Карта Шухурта
требует данных, получаемых выборочно
из процесса через примерно равные
интервалы. Интервалы могут быть заданы
по времени (например, ежечасно), либо по
количеству продукции (каждая партия).
Для каждой полученной подгруппы (выборки)
определяют одну или несколько
характеристик, таких как
![]() ,R
и т.п.
,R
и т.п.
Карта Шухарта – это график значений определяемых характеристик подгрупп в зависимости от их номеров (рисунок 11.1). Она имеет центральную линию (CL), соответствующую эталонному значению характеристики. При оценке того, находится ли процесс в статистическом управляемом состоянии, эталонным обычно служит среднее арифметическое значение рассматриваемых данных. При управлении процессом эталонным служит долговременное значение характеристики.
Карта Шухарта имеет две статистические определяемые границы относительно центральной линии, которые называют верхней контрольной границей (UCL) и нижней контрольной границей (LCL).
Контрольные границы
находятся на расстоянии
![]() от центральной линии, где
от центральной линии, где![]()
внутригрупповое стандартное отклонение
(используемой статистики). Границы
внутригрупповое стандартное отклонение
(используемой статистики). Границы
![]() указывают, что около 99,7% значений
характеристик подгрупп попадают в эти
пределы при условии, что процесс находится
в статистически управляемом состоянии.
Другими словами, есть риск равный 0,3%
(или в среднем 3 на тысячу случаев), что
нанесенная точка окажется вне контрольных
границ, когда процесс стабилен. В
результате неправильно решают, что
процесс вышел из состояния статистической
управляемости, и делают попытку выявления
несуществующей проблемы. В этом случае
говорят об ошибке первого рода.
указывают, что около 99,7% значений
характеристик подгрупп попадают в эти
пределы при условии, что процесс находится
в статистически управляемом состоянии.
Другими словами, есть риск равный 0,3%
(или в среднем 3 на тысячу случаев), что
нанесенная точка окажется вне контрольных
границ, когда процесс стабилен. В
результате неправильно решают, что
процесс вышел из состояния статистической
управляемости, и делают попытку выявления
несуществующей проблемы. В этом случае
говорят об ошибке первого рода.

Рисунок 11.1 Вид контрольной карты
Контрольные границы
иногда называют «границы действий».
Попадание точки вне этих границ считается
сигналом к действию. Часто на контрольной
карте проводят еще границы на расстоянии![]() .
Любое выборочное значение, попадающее
за эти границы, служит предостережением
о грозящей ситуации выхода процесса из
состояния статистической управляемости.
Эти границы иногда называют
«предупреждающими».
.
Любое выборочное значение, попадающее
за эти границы, служит предостережением
о грозящей ситуации выхода процесса из
состояния статистической управляемости.
Эти границы иногда называют
«предупреждающими».
Ошибки второго рода возникает, когда рассматриваемый процесс не управляем, а точки случайно оказываются внутри контрольных границ. В этом случае неверно заключают, что процесс статистически управляем и упускают возможность предупредить рост выхода несоответствующей продукции. Риск ошибки второго рода – функция трех факторов: ширины контрольных границ, степени неуправляемости и объема выборки.
Система карт
Шухарта учитывает только ошибки первого
рода, равные 0,3% в пределах границ
![]() .
.
Контрольные карты для количественных данных
Общие положения. Количественные данные представляют собой наблюдения, полученные с помощью измерения. Карты на основе таких данных имеют следующие преимущества по сравнению с контрольными картами для альтернативных данных:
для большинства процессов и их продукции на выходе имеются характеристики, которые могут быть измерены, так что применимость таких карт потенциально широка;
измеренное значение имеет больше информации, чем простое утверждение «да – нет»;
характеристики процесса могут быть проанализированы безотносительно установленных требований. Карты запускаются вместе с процессом и дают независимую картину того, на что процесс способен. После этого характеристики процесса можно сравнить или нет с установленными требованиями;
хотя получение количественных данных дороже, чем альтернативных, объемы подгрупп для количественных данных почти всегда гораздо меньше и при этом результат намного эффективнее. Это позволяет в некоторых случаях снизить общую стоимость контроля и уменьшить временной разрыв между производством продукции и корректирующим воздействием.
Для контрольных
карт, использующих количественные
данные, предполагается нормальное
(Гауссово) распределение для вариаций
внутри выборок. Коэффициенты для
вычисления контрольных границ выведены
из условия нормальности. Ранее нами
было показано, что выборочные средние
![]() имеют распределение, приближающиеся к
нормальному с ростом объема выборки,
даже когда отдельные наблюдения не
подчиняются нормальному закону. Это
обосновывает возможность предположения
о нормальности для
имеют распределение, приближающиеся к
нормальному с ростом объема выборки,
даже когда отдельные наблюдения не
подчиняются нормальному закону. Это
обосновывает возможность предположения
о нормальности для![]() – карт даже при малых объемах выборок
(4, 5 единиц).
– карт даже при малых объемах выборок
(4, 5 единиц).
Распределение
размахов R
и стандартных отклонений
![]() отличается от нормального, хотя
предположение нормальности используется
при оценке коэффициентов для вычисления
контрольных границ. Такие границы, как
правило, приемлемы для процедур принятия
эмпирических решений.
отличается от нормального, хотя
предположение нормальности используется
при оценке коэффициентов для вычисления
контрольных границ. Такие границы, как
правило, приемлемы для процедур принятия
эмпирических решений.
Карты средних (
 )
и размахов (R)
или выборочных стандартных отклонений
(
)
и размахов (R)
или выборочных стандартных отклонений
( ).Карты для
количественных данных отражают
состояние процесса через разброс
(изменчивость от единицы к единице)
и через расположение центра (среднее
процесса). Поэтому контрольные карты
для количественных данных почти
всегда применяют и анализируют парами
– одна карта для расположения и одна
для разброса. Наиболее часто используют
).Карты для
количественных данных отражают
состояние процесса через разброс
(изменчивость от единицы к единице)
и через расположение центра (среднее
процесса). Поэтому контрольные карты
для количественных данных почти
всегда применяют и анализируют парами
– одна карта для расположения и одна
для разброса. Наиболее часто используют
 ,
R
карту, (
,
R
карту, ( карту).
карту).
Для построения контрольных карт необходимо знать эталонное значение характеристики, которое задает положение центральной линии CL и положения контрольных границ UCL и LCL. Практический выбор этих значений зависит от того, известны ли стандартные значения генеральной совокупности или нет.
Предположим, что
из предыдущих исследований, либо из
каких-то соображений известны стандартные
значения генеральной совокупности:
![]() (
(![]() )
математическое ожидание и
)
математическое ожидание и
![]()
стандартное отклонение. В этом случае
в качестве CL
выбирается
стандартное отклонение. В этом случае
в качестве CL
выбирается
![]() (
(![]() ).
ГраницыUCL
и LCL
откладывается от CL
на расстоянии
).
ГраницыUCL
и LCL
откладывается от CL
на расстоянии
![]() , где
, где![]()
стандартное отклонение распределения
выборочных средних арифметических,
вычисляемое по формуле
стандартное отклонение распределения
выборочных средних арифметических,
вычисляемое по формуле
![]() .
Таким образом верхняя контрольная
граница откладывается на уровне
.
Таким образом верхняя контрольная
граница откладывается на уровне![]() ,
а нижняя контрольная граница на уровне
,
а нижняя контрольная граница на уровне![]() .
В этих формулах коэффициент
.
В этих формулах коэффициент![]() обозначают как
обозначают как![]() и окончательно записывают выражения
для положенийUCL
и LCL
следующим образом:
и окончательно записывают выражения
для положенийUCL
и LCL
следующим образом:![]()
![]()
![]() .
Как видно, значения
.
Как видно, значения![]() зависят от объема выборкиn.
Численные значения коэффициента
зависят от объема выборкиn.
Численные значения коэффициента
![]() представлены в таблице приложения Л.
представлены в таблице приложения Л.
Если стандартные
значения не известны оценку
![]() и
и![]() получают
по предварительным исследованиям. Для
этого из текущего процесса отбираютk
подгрупп (рекомендуется число 20…30) по
n
изделий (предположим по 4, 5 изделий).
Всего рекомендуется отбирать 100…150
деталей.
получают
по предварительным исследованиям. Для
этого из текущего процесса отбираютk
подгрупп (рекомендуется число 20…30) по
n
изделий (предположим по 4, 5 изделий).
Всего рекомендуется отбирать 100…150
деталей.
Оценку математического
ожидания генеральной совокупности
получают, вычислив среднюю арифметическую
![]() поk
значением выборочных средних:
поk
значением выборочных средних:
![]() ,
(11.1)
,
(11.1)
где
![]()
![]() (i=1,
2, .., k;
j
= 1, 2, .., n).
(i=1,
2, .., k;
j
= 1, 2, .., n).
Оценку стандартного отклонения генеральной совокупности можно произвести разными способами. Наиболее широко известны следующие три способа:
1. Вычисляют
дисперсию
![]() по всем имеющим наблюдениям
по всем имеющим наблюдениям![]() :
:![]() и стандартное отклонение:
и стандартное отклонение:![]() .
.
Методами
математической статистики можно
доказать, что
![]() не является несмещенной оценкой
не является несмещенной оценкой![]() и выполняется соотношение:
и выполняется соотношение:
![]() ,
(11.2)
,
(11.2)
где
![]() -
величина, зависящая от
-
величина, зависящая от![]() :
:
 ,
(11.3)
,
(11.3)
где Г символ гамма-функции.
В общем случае
![]() ,
однако, с возрастаниемm
она стремится к единице. Так, например,
при m
= 100
,
однако, с возрастаниемm
она стремится к единице. Так, например,
при m
= 100
![]() = 0,9975. Поэтому при большихm
стандартное отклонение
= 0,9975. Поэтому при большихm
стандартное отклонение
![]() можно спокойно использовать в качестве
асимптотически несмещенной оценки
можно спокойно использовать в качестве
асимптотически несмещенной оценки![]() .
В этом случае контрольные границы
определяется следующим образом:
.
В этом случае контрольные границы
определяется следующим образом:
![]() .
(11.4)
.
(11.4)
Описанный способ
требует большой вычислительной работы,
вследствие чего на практике используется
редко.![]()
2. Оценка стандартного
отклонения по
![]() .
.
В этом случае вычисляют для каждой из k подгрупп дисперсию и стандартное отклонение:
![]() ,
(11.5)
,
(11.5)
* )
Использование программ типа «STATISTICA»
значительно упрощает обработку данных.
)
Использование программ типа «STATISTICA»
значительно упрощает обработку данных.
![]() ,
(11.6)
,
(11.6)
где (i = 1, 2, …, k).
Затем для k
стандартных отклонений подгрупп
![]() определяют среднее арифметическое:
определяют среднее арифметическое:
![]() .
(11.7)
.
(11.7)
В математической
статистике доказывается, что
![]() не является несмещенной оценкой для
не является несмещенной оценкой для![]() и что:
и что:
![]()
![]() ,
(11.8)
,
(11.8)
где
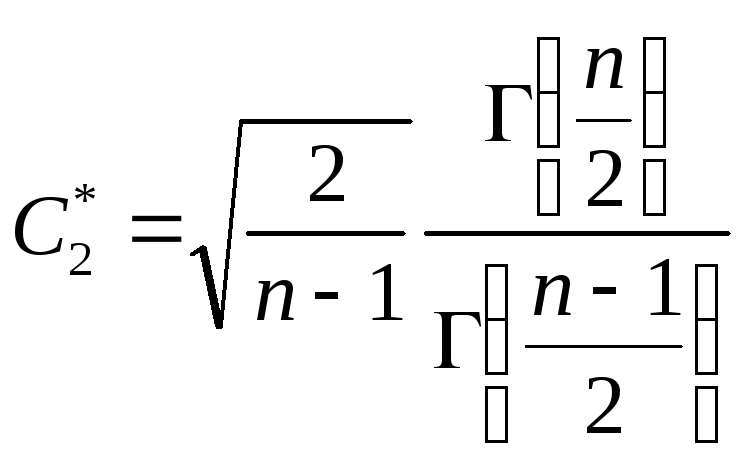
величина, зависящая от объёма выборки
n.
величина, зависящая от объёма выборки
n.
![]() соответствует
соответствует![]() ,
если заменитьm
на n.
Поскольку n
невелико, то
,
если заменитьm
на n.
Поскольку n
невелико, то
![]() значительно ниже единицы. Так, например,
дляn
= 2
значительно ниже единицы. Так, например,
дляn
= 2
![]() =0,798,
дляn
= 5
=0,798,
дляn
= 5
![]() =0,960.
=0,960.
В качестве
несмещенной оценки для
![]() в этом случае используют величину:
в этом случае используют величину:![]() ,
а выражение для контрольных границ
запишется следующим образом:
,
а выражение для контрольных границ
запишется следующим образом:
![]()
![]() .
(11.9)
.
(11.9)
Численные значения
коэффициента
![]() представлены в таблице приложения Л.
представлены в таблице приложения Л.
Описанный способ
используют лишь тогда, когда строятся
совместно карты![]() .
.
3. Чаще всего в
технике используют оценку параметра
![]() с помощью размахаR,
определяемого в виде:
с помощью размахаR,
определяемого в виде:
![]() .
.
Теорией и практикой
доказано, что стандартное отклонение
выборки
![]() и ее размахR
находятся в прямой зависимости друг от
друга. Для каждой из k
подгрупп объема n
вычисляют размахи R
и выводят их среднее арифметическое:
и ее размахR
находятся в прямой зависимости друг от
друга. Для каждой из k
подгрупп объема n
вычисляют размахи R
и выводят их среднее арифметическое:
![]()
![]() .
(11.10)
.
(11.10)
Величина
![]() ,
как и
,
как и![]() учитывает рассеивание только внутри
проб, но не между ними.
учитывает рассеивание только внутри
проб, но не между ними.
В статистической
теории оценок показывают, что
![]() ,
т.е.
,
т.е.![]() представляет собой несмещенную оценку
для
представляет собой несмещенную оценку
для![]() .
Коэффициентыd2
зависят от объема подгруппы n.
Их получают при выводе закона распределения
выборочной функции
.
Коэффициентыd2
зависят от объема подгруппы n.
Их получают при выводе закона распределения
выборочной функции
![]() .
Вывод этот математически достаточно
сложен. Впервые таблицы значенийd2
рассчитаны
Пирсоном.
.
Вывод этот математически достаточно
сложен. Впервые таблицы значенийd2
рассчитаны
Пирсоном.
Выражение для
контрольных границ карты
![]() запишется следующим образом:
запишется следующим образом:
![]() ,
(11.11)
,
(11.11)
где
![]() .
(11.12)
.
(11.12)
Численные значения
коэффициентов
![]() и
и![]() представлены в таблице приложения Л
для разныхn.
представлены в таблице приложения Л
для разныхn.
При определении средней линии и границ регулирования R- карты учитывают, что распределение размахов выборок одинакового объема ассиметрично (рисунок 11.2), т.к. размах является положительной величиной и теоретически может принимать какие угодно значения.
Распределение размахов исследовалось и практически и теоретически. Вывод формул для расчета контрольных границ карты R базируется на законе распределения выборочной функции R, который здесь подробно не рассматривается.
Как уже упоминалось,
при малых n
значения S
и R
связаны тесной корреляционной
зависимостью. Вследствие этого среднее
квадратичное отклонение распределения
размахов
![]() можно вычислить из
можно вычислить из![]() генеральной совокупности с помощью
коэффициента
генеральной совокупности с помощью
коэффициента![]() ,
зависящего отn:
,
зависящего отn:
![]() .
Связь между средним значением распределенияR
и
.
Связь между средним значением распределенияR
и
![]() уже известна:
уже известна:![]() .
.

Рисунок 11.2 Распределение размахов
Вычисление значений CL, UCL и LCL R-карты производится следующим образом.
1. Если
![]() генеральной совокупности известно, то
среднее значениеR-карты
CL
вычисляется как:
генеральной совокупности известно, то
среднее значениеR-карты
CL
вычисляется как:
![]() ,
границы регулированияUCL
и LCL
в этом случае определяются следующим
выражением:
,
границы регулированияUCL
и LCL
в этом случае определяются следующим
выражением:
![]() ,
(11.13)
,
(11.13)
или:
![]() ,
(11.14)
,
(11.14)
![]() .
(11.15)
.
(11.15)
2. Если
![]() генеральной совокупности неизвестно,
то его оценку вычисляют поR
с помощью коэффициентов
генеральной совокупности неизвестно,
то его оценку вычисляют поR
с помощью коэффициентов
![]() и
и![]() .
Границы регулирования запишутся в этом
случае следующим образом:
.
Границы регулирования запишутся в этом
случае следующим образом:
 ,
(11.16)
,
(11.16)
 .
(11.17)
.
(11.17)
Значения коэффициентов
![]() ,
,![]() ,
,![]() ,
,![]() приведены в таблице приложения Л. Они
зависят от объема выборки. Коэффициенты
приведены в таблице приложения Л. Они
зависят от объема выборки. Коэффициенты![]() для нижней контрольной границы равны
нулю дляn
от 2 до 6.
для нижней контрольной границы равны
нулю дляn
от 2 до 6.
Положение средней
линии и границ регулирования
![]() -карты
приведем без выводов в виде только
справочных значений.
-карты
приведем без выводов в виде только
справочных значений.
Если стандартные значения заданы, то:
![]() ,
,
![]() ,
,![]() .
(11.18)
.
(11.18)
Если стандартные значения не заданы, то:
![]() ,
,
![]() ,
,![]() .
(11.19)
.
(11.19)
Метод управления и интерпретации контрольных карт для количественных данных. Система карт Шухарта опирается на следующие условия: если изменчивость процесса от единице к единице и среднее процесса остается постоянными на данных уровнях (оцененных соответственно по
 и
и ),
то размах
),
то размах и средние
и средние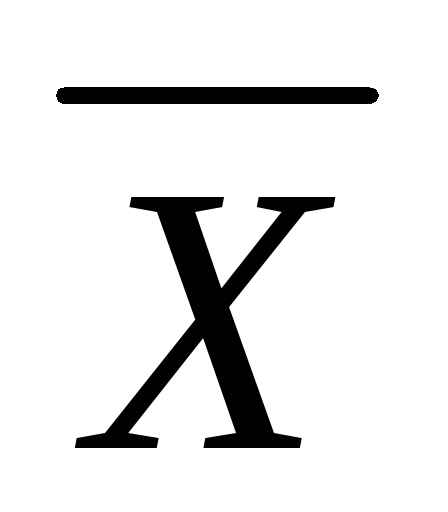 отдельных подгрупп будут меняться
только случайным образом и редко
выходить за контрольные границы. Не
допускаются очевидные тренды или
структуры данных, кроме возникающих
случайно с некоторой долей вероятности.
отдельных подгрупп будут меняться
только случайным образом и редко
выходить за контрольные границы. Не
допускаются очевидные тренды или
структуры данных, кроме возникающих
случайно с некоторой долей вероятности.
При этом
![]() -карта
показывает, где находится среднее
процесса и какова его стабильность. Эта
же карта выявляет нежелательные вариации
между подгруппами и вариации относительно
их среднего.
-карта
показывает, где находится среднее
процесса и какова его стабильность. Эта
же карта выявляет нежелательные вариации
между подгруппами и вариации относительно
их среднего.![]() -
карта выявляет любую нежелательную
вариацию внутри подгрупп и служит
индикатором изменчивости процесса. Эта
мера состоятельности и однородности
процесса. Если
-
карта выявляет любую нежелательную
вариацию внутри подгрупп и служит
индикатором изменчивости процесса. Эта
мера состоятельности и однородности
процесса. Если![]() -карта
показывает, что вариации внутри подгрупп
не изменяются, то это означает, что
процесс остается в статистически
управляемом состоянии. Если
-карта
показывает, что вариации внутри подгрупп
не изменяются, то это означает, что
процесс остается в статистически
управляемом состоянии. Если![]() ‑карта
показывает, что процесс вышел из
управляемого состояния или уровень на
‑карта
показывает, что процесс вышел из
управляемого состояния или уровень на![]() -карте
возрастает, то это может означать,
что-либо отдельные подгруппы подверглись
разной обработке, либо в процессе
действует несколько разных систем
причинно-следственных связей.
-карте
возрастает, то это может означать,
что-либо отдельные подгруппы подверглись
разной обработке, либо в процессе
действует несколько разных систем
причинно-следственных связей.
На
![]() -карту
могут повлиять условия, при которых
процесс вышел из состояния статистической
управляемости по
-карту
могут повлиять условия, при которых
процесс вышел из состояния статистической
управляемости по![]() -карте.
Поэтому
-карте.
Поэтому![]() -
карту анализируют первой.
-
карту анализируют первой.
Процедура управления выглядит следующим образом:
Собирают и анализируют данные. Вычисляют значения средних арифметических и размахов.
Строят
 -карту.
Сопоставляют нанесенные точки размахов
с контрольными границами. Выделяют
точки вне границ, особые структуры или
тренды. Для каждого сигнала о наличии
неслучайной причины в значении размаха
проводят анализ операций процесса,
чтобы определить причину. Проводят
корректирующие действия для предотвращение
повторения данной причины.
-карту.
Сопоставляют нанесенные точки размахов
с контрольными границами. Выделяют
точки вне границ, особые структуры или
тренды. Для каждого сигнала о наличии
неслучайной причины в значении размаха
проводят анализ операций процесса,
чтобы определить причину. Проводят
корректирующие действия для предотвращение
повторения данной причины.Исключают все подгруппы, на которые повлияла неслучайная причина, затем пересчитывают и наносят на карту новые средний размах
 и контрольные границы. Необходимо
получить подтверждение того, что все
точки размахов при сравнении с новыми
границами указывают на статистическую
управляемость. Если требуется, повторяют
последовательность действий «идентификация
- корректировка-пересчет».
и контрольные границы. Необходимо
получить подтверждение того, что все
точки размахов при сравнении с новыми
границами указывают на статистическую
управляемость. Если требуется, повторяют
последовательность действий «идентификация
- корректировка-пересчет».Если некоторые подгруппы исключены из R-карты из-за выявленных особых причин, их надо исключить и из
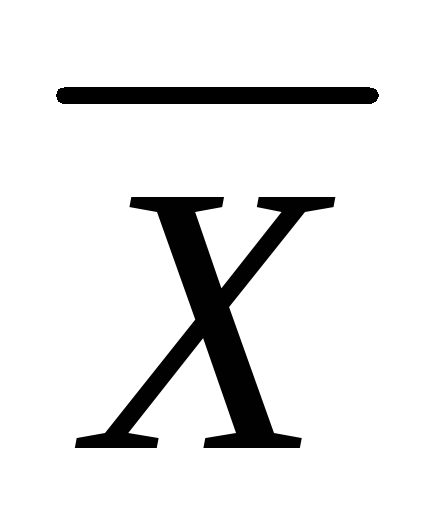 -карты.
Пересмотренные значения
-карты.
Пересмотренные значения и
и надо использовать для пересчета пробных
контрольных границ для средних
надо использовать для пересчета пробных
контрольных границ для средних .
.
Примечание. Исключение подгрупп, представляющих причину выхода процесса из состояния статистической управляемости, это не «исключение плохих данных». Скорее, здесь исключаются точки, на которые повлияли известные неслучайные причины, и мы получаем лучшую оценку основного уровня изменчивости из-за случайных причин. Это дает наиболее подходящую основу для контрольных границ, применение которых позволяет наиболее эффективным образом обнаруживать будущие проявления неслучайных причин вариаций.
Когда размахи находятся в статистически управляемом состоянии, разброс процесса (отклонения внутри подгрупп) считается стабильным. В этом случае можно проанализировать средние арифметические, чтобы увидеть, меняется ли со временем среднее положение процесса.
Теперь строят
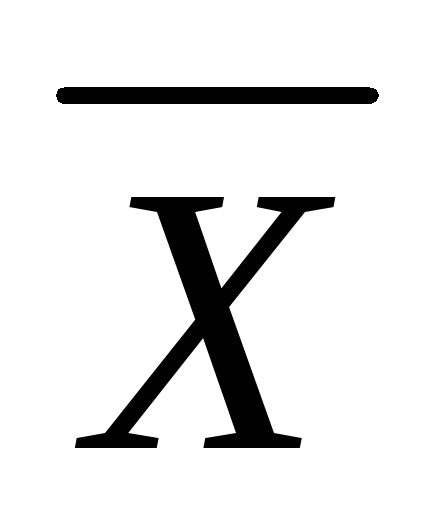 -карту
и сравнивают точки с контрольными
границами. Выделяют точки вне границ,
необычные структуры точек или тренды.
Также как и дляR-карты
необходимо анализировать любое из
состояний статистической неуправляемости
и проводить корректирующие и превентивные
меры. Надо исключить точки, которые
характеризуют это состояние и для
которых были найдены неслучайные
причины.
-карту
и сравнивают точки с контрольными
границами. Выделяют точки вне границ,
необычные структуры точек или тренды.
Также как и дляR-карты
необходимо анализировать любое из
состояний статистической неуправляемости
и проводить корректирующие и превентивные
меры. Надо исключить точки, которые
характеризуют это состояние и для
которых были найдены неслучайные
причины.
Повторно вычисляют
и наносят на график новое среднее
процесса (![]() )
и контрольные границы. Проверяют, чтобы,
по сравнению с новыми границами, все
точки демонстрировали статистически
управляемое состояние, при необходимости
возобновляя последовательные действия:
«идентификация – корректировка –
пересчет».
)
и контрольные границы. Проверяют, чтобы,
по сравнению с новыми границами, все
точки демонстрировали статистически
управляемое состояние, при необходимости
возобновляя последовательные действия:
«идентификация – корректировка –
пересчет».
Если исходные данные для установления эталонных значений контрольных границ располагаются устойчиво внутри пробных пределов, расширяют границы, чтобы охватить будущие данные. Исполнители (оператор или (и) мастер) должны пользоваться этими границами для последующего управления процессами, реагировать на сигналы о выходе процесса из управляемого состояния на любой из
 иR-карт
и выполнять надлежащие действия.
иR-карт
и выполнять надлежащие действия.
Проверка структур на особые причины. Как было сказано выше, основным критерием выхода процесса из состояния статистической управляемости является попадание одной из точек на контрольных картах вне контрольных границ. Помимо этого необходимо рассмотреть расположение точек на наличие особых структур также маловероятных, как и выход точки за контрольные границы. В практике применения контрольных карт используют определенный набор таких структур. Так, например, в ГОСТ 50779.42-99 (ИСО 8258-91) для
 -карт
и Х-карт индивидуальных значений
предлагается набор из семи дополнительных
критериев, которые схематически
показанных на рисунках 11.3 – 11.9.
-карт
и Х-карт индивидуальных значений
предлагается набор из семи дополнительных
критериев, которые схематически
показанных на рисунках 11.3 – 11.9.
Критерий 1 – девять точек подряд в зоне С или по одну сторону от центральной линии (рисунок 11.3).

Рисунок 11.3 – Девять точек подряд в зоне С
или по одну сторону от центральной линии
Критерий 2 – Шесть возрастающих или убывающих точек подряд (рисунок 11.4).
![]()

Рисунок 11.4 – Шесть возрастающих или убывающих точек подряд
Критерий 3 – Четырнадцать попеременно возрастающих и убывающих точек (рисунок 11.5).

Рисунок 11.5 – Четырнадцать попеременно
возрастающих и убывающих точек
Критерий 4 — Две из трех последовательных точек в зоне А или вне её (рисунок 11.6).

Рисунок 11.6 – Две из трех последовательных точек
в зоне А или вне её
Критерий 5 – Четыре из пяти последовательных точек в зоне В или вне её (рисунок 11.7).

Рисунок 11.7 – Четыре из пяти последовательных точек
в зоне В или вне её
Критерий 6 – Пятнадцать последовательных точек в зоне С выше или ниже центральной линии (рисунок 11.8).

Рисунок 11.8 – Пятнадцать последовательных точек
в зоне С выше или ниже центральной линии
Критерий 7 – Восемь последовательных точек по обе стороны центральной линии и ни одной в зоне С (рисунок 11.9).

Рисунок 11.9 – Восемь последовательных точек
по обе стороны центральной линии и ни одной в зоне С
Для применения
этих критериев контрольная карта делится
на шесть равных зон шириной, равной σ.
Эти зоны обозначаются как А, В, С, С, В, А
и располагаются симметрично центральной
линии. Предполагается нормальное
распределение соответственно
![]() и индивидуальных значений.
и индивидуальных значений.
Появление каждой
из предложенных структур точек также
маловероятно, как выход точки за
контрольную границу и это можно рассчитать
методами теории вероятности. Действительно,
рассчитаем, для примера, вероятность
того, что 8 точек подряд будут находиться
по одну сторону от центральной линии.
Вероятность одного попадания точки в
данную область контрольной карты равна
0,5. Вероятность попадания восьми точек
подряд равна по правилу умножения
вероятностей (0,5)8
=0.004 (0,4%). Вероятность попадания девяти
точек подряд (критерий
1) равна
(0,5)9
=0,0019 (![]() 0,2),
что чуть меньше, чем вероятность выхода
одной точки вне контрольной границы
(0,3%).
0,2),
что чуть меньше, чем вероятность выхода
одной точки вне контрольной границы
(0,3%).
Рассмотренный набор критериев можно принять за основу. Но при работе с контрольными картами необходимо обращать внимание на любую необычную структуру точек, которая может указывать на проявление особых (неслучайных) причин. Поэтому эти критерии следует рассматривать только как примеры ситуаций, когда может быть установлено проявление неслучайных причин. Появление любого из случаев, описанных в этих критериях, указание на присутствие особых причин, которые должны быть проанализированы и скорректированы.
Управление процессом и возможности процесса
Назначение системы управления процессом состоит в получении статистического сигнала о наличии особых (неслучайных) причин вариаций. Систематическое устранение особых причин избыточной изменчивости приводит процесс в состояние статистической управляемости. Если процесс находится в статистически управляемом состоянии, качество продукции предсказуемо, и процесс пригоден для удовлетворения требований, установленных в нормативных документах.
Возможности
процесса определяются полной изменчивостью
(разбросом процесса), обусловленной
обычными причинами, т.е. минимальной
изменчивостью, которая остается после
устранения всех неслучайных
причин. Возможности процесса представляют
показатели самого процесса в статистически
управляемом состоянии. Процесс сначала
приводят в такое состояние, а затем
определяют его возможности. Таким
образом, определение возможностей
процесса начинается после того, как
задачи управления по
![]() -
иR-картам
решена, т.е. особые причины выявлены,
проанализированы, скорректированы и
их повторение предотвращено. Текущие
контрольные карты должны демонстрировать
сохранение процесса в статистически
управляемом состоянии, по крайне мере,
для 25 подгрупп.
Далее разброс данных на выходе процесса
сравнивается с техническими требованиями
для подтверждения того, что эти требования
могут быть уверенно выполнены.
-
иR-картам
решена, т.е. особые причины выявлены,
проанализированы, скорректированы и
их повторение предотвращено. Текущие
контрольные карты должны демонстрировать
сохранение процесса в статистически
управляемом состоянии, по крайне мере,
для 25 подгрупп.
Далее разброс данных на выходе процесса
сравнивается с техническими требованиями
для подтверждения того, что эти требования
могут быть уверенно выполнены.
В общем случае возможности процесса определяют индексом возможностей процесса Ср (PCI):
![]() ,
(11.20)
,
(11.20)
где UTL верхнее предельно допустимое значение контролируемого параметра;
LTL нижнее предельно допустимое значение контролируемого параметра;
![]() оценивают по
средней изменчивости внутри подгрупп
и выражают как
оценивают по
средней изменчивости внутри подгрупп
и выражают как
![]() или
или![]() .
.
При Ср меньше 1 возможности процесса неприемлемы, а при Ср равном 1, процесс находится на грани требуемых возможностей. На практике в качестве минимально приемлемого значения берется Ср =1,33, поскольку всегда есть некоторые вариации в выборках, и нет процессов, которые всегда находятся в статистически управляемом состоянии.
Следует отметить, что Ср измеряет только отношение разброса процесса и допуска, а положение или центрирование процесса не учитывается. При высоких значениях Ср все-таки возможен выход доли значений за установленные пределы. Поэтому важно также оценивать расстояние между средним процесса и ближайшим предельно допустимым значением. Дальнейшее обсуждение этого вопроса выходит за рамки данного раздела.
В качестве руководства к действию можно использовать процедуру, схематически представленную на рисунке 11.10.

Рисунок 11.10 – Стратегия совершенствования процесса
Контрольные карты для альтернативных данных
Альтернативные данные представляют собой наблюдения, фиксирующие наличие или отсутствие некоторых характеристик (или признаков) у каждой единицы рассматриваемой подгруппы. На основе этих данных производится подсчет числа единиц, обладающих или не обладающих данным признаком, или число таких событий в единице продукции, группе или области. Альтернативные данные в общем случае могут быть получены быстро и дешево, для сбора их не требуется специального обучения. В таблице 11.1 приведены формулы контрольных границ для контрольных карт, использующих альтернативные данные.
Таблица 11.1 – Формулы контрольных границ карт Шухарта для альтернативных данных
|
Статистика |
Стандартные значения не заданы |
Стандартные значения заданы | ||
|
Центральная линия |
|
Центральная линия |
| |
|
р доли не соответствующих единиц продукции |
|
|
р0 |
|
|
np число несоответствующих единиц продукции |
|
|
|
|
|
с число несоответствий |
|
|
|
|
|
u число несоответствий, приходящих на единицу продукции |
|
|
|
|
|
Примечание:
р0,
| ||||
В случае контрольных карт для количественных данных принято ведение пары контрольных карт: для управления средним и управления рассеянием, так как исходное распределение предполагается нормальным и зависит от этих двух параметров. При использовании контрольных карт для альтернативных данных достаточно одной карты, так как предлагаемое распределение имеет только один независимый параметр средний уровень. При этом р- и пр- карты основаны на биноминальном распределении, а с- и u-карты на распределении Пуассона.
Расчеты для этих карт одинаковы, за исключением случаев непостоянства объёма подгрупп. Когда объем подгрупп постоянен, для каждой подгруппы могут быть выбраны одни и те же контрольные границы. Если число контролируемых единиц в каждой подгруппе различно, должны быть рассчитаны контрольные границы отдельно для каждого объема подгруппы. Таким образом, пр- и с- карты могут быть применены при постоянном объеме подгруппы, а р- и u- карты – в любой ситуации.
Когда объем
подгруппы изменяется от выборки к
выборке, для каждой подгруппы рассчитывают
свои контрольные границы, при этом, чем
меньше объем подгруппы, тем шире полоса
между этими границами, и наоборот. Если
объем подгрупп меняется несущественно,
то можно ограничиться одним набором
контрольных границ, основанным на
среднем объеме подгруппы. Для практических
целей достаточно, если объемы подгрупп
находятся в пределах
![]() 25%
целевого объёма подгруппы.
25%
целевого объёма подгруппы.
Альтернативная процедура для ситуаций, в которых объем подгруппы меняется существенно использование нормированных переменных. Например, вместо значений р наносят нормированные значения:
 или
или
 ,
(11.21)
,
(11.21)
в зависимости от того, установлено или нет стандартное значение для р. Центральная линия и контрольные границы в этом случае остаются постоянными независимо от объема подгруппы и выражаются следующим образом: центральна линия равна 0, UCL = 3, LCL = 3
Обычно р-карту
используют для определения среднего
процента несоответствующих единиц,
обнаруженных за определенный период
времени. Она привлекает внимание
персонала процесса и управляющих к
любым изменениям этого среднего. Процесс
признается находящимся в состоянии
статистической управляемости так же,
как и при использовании
![]() -
иR-карт.
Если все выборочные точки ложатся внутри
пробных контрольных границ без выбросов,
указывающих на наличие особых причин,
то о процессе можно сделать заключение,
что он управляем. В этом случае средняя
доля несоответствующих
-
иR-карт.
Если все выборочные точки ложатся внутри
пробных контрольных границ без выбросов,
указывающих на наличие особых причин,
то о процессе можно сделать заключение,
что он управляем. В этом случае средняя
доля несоответствующих
![]() единиц берется как стандартное значение
для доли несоответствующих единиц
единиц берется как стандартное значение
для доли несоответствующих единиц![]() .
.
Контрольные карты кумулятивных сумм
При использовании контрольных карт Шухарта решение о том, что процесс вышел из состояния статистической управляемости принимается при регистрации одного из сигнальных признаков, например, выхода очередной точки за контрольные границы. В то же время информацию о намечающейся тенденции к разладке процесса на такой карте разглядеть обычно не удается. В этом смысле более наглядными являются контрольные карты кумулятивных сумм.
Методика построения
таких карт заключается в следующем.
Если есть ряд значений некоторого
признака
![]() ,
то образование кумулятивных сумм
(кусумм) будет происходить следующим
образом:
,
то образование кумулятивных сумм
(кусумм) будет происходить следующим
образом:
![]() ,
,
![]() ,
,
![]() ,
,
где k– константа, представляющая собой некоторое заранее определенное значение.
Вычисленные и нанесенные на график в порядке их появления кумулятивные суммы образуют кусумм-карту.
Константа kможет принимать любое значение, даже нулевое, однако чаще всего ее приравнивают математическому ожиданию исследуемого признака, или к номинальному значению параметра процесса.
Если среднее
значение параметра процесса возрастает,
то будет иметь место и общий рост уровня
кусуммы, поскольку все большее число
значений
![]() будут положительными. Если среднее
значение параметра будет уменьшаться,
то и график кусумм будет стремиться
вниз. Другими словами, изменение среднего
значения исходных данных приведет к
изменению угла наклона графика кусумм.
будут положительными. Если среднее
значение параметра будет уменьшаться,
то и график кусумм будет стремиться
вниз. Другими словами, изменение среднего
значения исходных данных приведет к
изменению угла наклона графика кусумм.
Фактическая величина значения кусуммы в отдельной точке не имеет никакого значения, так как из-за мелких случайных колебаний параметров процесса на отдельных участках графика кусумм могут проявляться различные тенденции в угле наклона. И только построение среднего наклона графика кусумм позволяет установить, имеет ли место устойчивая тенденция изменения исследуемого параметра в данный временной период.
Порядок расчетов и построения карты кумулятивных сумм рассмотрим на следующем примере.
При анализе процентного содержания кремния в стальных образцах были получены следующие цифры в %: 2,30; 2,25; 2,35; 2,20; 2,10; 2,15; 2,15; 2,20; 2,10; 2,35. Необходимо построить кусумм – карту для номинального значения 2,25%.
Данные для построения можно получит следующим образом:
|
№ образца |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Результат |
2,30 |
2,25 |
2,35 |
2,20 |
2,10 |
2,15 |
2,15 |
2,20 |
2,10 |
2,35 |
|
Разность |
+0,05 |
0, |
+0,10 |
-0,05 |
-0,15 |
-0,10 |
-0,10 |
-0,5 |
-0,15 |
+0,10 |
|
Кусумма |
+0,05 |
+0,05 |
+0,15 |
0,10 |
-0,05 |
-0,15 |
-0,25 |
-0,30 |
-0,45 |
-0,35 |
График кумулятивных сумм показан на рисунке 11.11.

Рисунок 11.11 Карта кумулятивных сумм для содержания кремния в стальных образцах
Из построенной кусумм-карты хорошо видна тенденция пониженного содержания кремния в исследуемых образцах.
Для карт кумулятивных сумм мерой измерения исследуемой случайной величины является наклон графика. Если график кумулятивной суммы горизонтален (имеет нулевой наклон), то технологический процесс находится в оптимальном режиме. В противном случае процесс не отличается стабильностью.
График кумулятивных сумм более чувствителен к выявлению изменений в уровне исследуемого параметра, чем традиционные графики. Изучение карты кумулятивных сумм позволяет увязать обнаруженные тенденции изменения контрольного признака с реальными внешними влияющими факторами и событиями, вызывающими изменение параметра в ту или иную сторону от установленного значения.
Контрольные вопросы
Что такое контрольная карта?
Какие виды изменчивости различает теория контрольных карт?
Какой вид изменчивости процесса выявляют контрольные карты?
Какие виды контрольных карт вы знаете?
Назовите типы контрольных карт Шухарта для количественных данных.
Назовите типы контрольных карт Шухарта для альтернативных данных.
Какая характеристика служит эталонным значением при определении положения центральной линии контрольной карты Шухарта предназначенной для управления процессом?
На каком расстоянии от центральной линии контрольной карты Шухарта располагаются ее контрольные границы?
Что означает риск первого рода при интерпретации контрольной карты Шухарта?
Что означает риск второго рода при интерпретации контрольной карты Шухарта?
Ошибки какого рода учитывает система карт Шухарта?
Какие преимущества имеют контрольные карты на основе количественных данных по сравнению с контрольными картами для альтернативных данных?
Какой закон распределения выборочных данных положен в основу определения коэффициентов для вычисления контрольных границ контрольных карт?
Для каких выборочных характеристик из набора:
 ,R
и
,R
и
 предположение о нормальности их
распределения дает наиболее достоверные
результаты при определения коэффициентов
для вычисления контрольных границ
контрольных карт?
предположение о нормальности их
распределения дает наиболее достоверные
результаты при определения коэффициентов
для вычисления контрольных границ
контрольных карт?Как определяются коэффициенты для вычисления контрольных границ
 - карт, если
известны стандартные значения генеральной
совокупности:
- карт, если
известны стандартные значения генеральной
совокупности:
 (
( )
- математическое ожидание и
)
- математическое ожидание и -
стандартное отклонение?
-
стандартное отклонение?Как определяются коэффициенты для вычисления контрольных границ
 - карт, если
стандартные значения генеральной
совокупности:
- карт, если
стандартные значения генеральной
совокупности:
 (
( )
- математическое ожидание и
)
- математическое ожидание и -
стандартное отклонение не известны?
-
стандартное отклонение не известны?Как определяются средняя линия и контрольные границы R- карты?
Опишите последовательность использования
 -,R-
карт для
управления процессом.
-,R-
карт для
управления процессом.Почему при управлении процессом с использованием
 -,R-
карт анализ начинают с R-
карты?
-,R-
карт анализ начинают с R-
карты?Почему исключение из контрольных карт подгрупп, представляющих причину выхода процесса из состояния статистической управляемости, это не «исключение плохих данных»?
Какое расположение точек на контрольной карте является сигналом о выходе процесса из состояния статистической управляемости?
Почему попадание девяти точек подряд на контрольной
 -
карте в зону С или по одну сторону от
центральной линии так же значимо при
оценке статистической управляемости
процесса, как и выход точки за контрольную
границу?
-
карте в зону С или по одну сторону от
центральной линии так же значимо при
оценке статистической управляемости
процесса, как и выход точки за контрольную
границу?Как оцениваются возможности процесса?
Опишите алгоритм действий по совершенствованию процесса с использованием
 -,R-
карт и оценкой возможностей процесса.
-,R-
карт и оценкой возможностей процесса.В чем состоят преимущества контрольных карт, использующих альтернативные данные?
Как рассчитываются положение средней линии и контрольных границ для р- карты?
Как рассчитываются положение средней линии и контрольных границ для nр- карты?
Как рассчитываются положение средней линии и контрольных границ для с - карты?
Как рассчитываются положение средней линии и контрольных границ для u- карты?
На каком законе распределения основаны расчеты контрольных границ р- и пр- карт?
На каком законе распределения основаны расчеты контрольных границ с- и u - карт?
В чем состоят особенности расчета контрольных границ р- и u- карт когда объем подгрупп изменяется от выборки к выборке?
Что такое контрольная карта кумулятивных сумм?
Какое значение следует принимать для константы k при построении контрольной карты кумулятивных сумм?
Что является мерой оценки состояния процесса при построении контрольной карты кумулятивных сумм?
В чем состоят преимущества контрольной карты кумулятивных сумм перед обычными контрольными картами?
Задачи для самостоятельной работы
Рассчитайте вероятность того, что 9 точек подряд на контрольной Х-карте будут находиться в зоне С или по одну сторону от центральной линии .
Рассчитайте вероятность того, что две из трех последовательных точек на контрольной Х-карте будут находиться в зоне А или вне её.
Рассчитайте вероятность того, что четыре из пяти последовательных точек на контрольной Х-карте будут находиться в зоне В или вне её.
Рассчитайте вероятность того, что пятнадцать последовательных точек на контрольной Х-карте будут находиться в зоне С выше или ниже центральной линии.
Рассчитайте вероятность того, что восемь последовательных точек на контрольной Х-карте будут находиться по обе стороны центральной линии и ни одной в зоне С.
Менеджер по качеству импортера чая предъявляет следующие требования к процессу упаковки, известные ему из аналогичных упаковочных процессов: средний вес упаковки 100,6 г; стандартное отклонение 1,4 г.
Для контроля были взяты 25 выборок объемом 5 пачек. Значение их средних и размахов приведены в таблице 11.2.
Таблица 11.2 Результаты обработки измерений 25 выборок пачек чая в граммах
|
№ п/п |
Среднее подгруппы |
Размах подгруппы |
№ п/п |
Среднее подгруппы |
Размах подгруппы |
|
1 |
100,6 |
3,4 |
14 |
99,4 |
5,1 |
|
2 |
101,3 |
4,0 |
15 |
99,4 |
4,5 |
|
3 |
99,6 |
2,2 |
16 |
99,6 |
4,1 |
|
4 |
100,5 |
4,5 |
17 |
99,3 |
4,7 |
|
5 |
99,9 |
4,8 |
18 |
99,9 |
5,0 |
|
6 |
99,5 |
3,8 |
19 |
100,5 |
3,9 |
|
7 |
100,4 |
4,1 |
20 |
99,5 |
4,7 |
|
8 |
100,5 |
1,7 |
21 |
100,1 |
4,6 |
|
9 |
101,1 |
2,2 |
22 |
100,4 |
4,4 |
|
10 |
100,3 |
4,6 |
23 |
101,1 |
4,9 |
|
11 |
100,1 |
5,0 |
24 |
99,9 |
4,7 |
|
12 |
99,6 |
6,1 |
25 |
99,7 |
3,4 |
|
13 |
99,2 |
3,5 |
|
|
|
Построить
![]() ,R-
карты и оценить статистическую
управляемость процесса упаковки чая.
,R-
карты и оценить статистическую
управляемость процесса упаковки чая.
Наладчик произвел настройку автоматического станка на номинальный размер 35 и стандартное отклонение 4,2. Для проверки правильности настройки станка проведен контроль колебаний качества изделий от партии к партии. Для этого из каждой партии бралась малая выборка объемом 5 деталей. В таблице 11.3 показаны результаты обработки данных десяти выборок.
Таблица 11.3 Данные контроля показателя качества
|
№ парии |
Средняя арифметическая |
Размах |
|
1 |
36,0 |
6,6 |
|
2 |
31,4 |
0,5 |
|
3 |
39,0 |
15,1 |
|
4 |
35,6 |
8,8 |
|
5 |
38,8 |
2,2 |
|
6 |
41,6 |
3,5 |
|
7 |
36,2 |
9,6 |
|
8 |
38,0 |
9,0 |
|
9 |
31,4 |
20,6 |
|
10 |
29,2 |
21,7 |
Оцените возможности статистической управляемости процесса обработки деталей на автоматическом станке.
В таблице 11.4 приведены результаты измерений внешнего радиуса втулки. Каждые полчаса делались четыре измерения. Всего взято 20 выборок.
Таблица 11.4 Производственные данные для внешнего радиуса втулки
|
№ подгруппы |
Радиус | |||
|
Х1 |
Х2 |
Х3 |
Х4 | |
|
1 |
0,1898 |
0,1729 |
0,2067 |
0,1898 |
|
2 |
0,2012 |
0,1913 |
0,1878 |
0,1921 |
|
3 |
0,2217 |
0,2192 |
0,2078 |
0,1980 |
|
4 |
0,1832 |
0,1812 |
0,1963 |
0,1800 |
|
5 |
0,1692 |
0,2263 |
0,2066 |
0,2091 |
|
6 |
0,1621 |
0,1832 |
0,1914 |
0,1783 |
|
7 |
0,2001 |
0,1937 |
0,2169 |
0,2082 |
|
8 |
0,2401 |
0,1825 |
0,1910 |
0,2264 |
Окончание таблицы 11.4
|
№ подгруппы |
Радиус | |||
|
Х1 |
Х2 |
Х3 |
Х4 | |
|
|
Х1 |
Х2 |
Х3 |
Х4 |
|
10 |
0,1783 |
0,1715 |
0,1829 |
0,1961 |
|
11 |
0,2166 |
0,1748 |
0,1960 |
0,1923 |
|
12 |
0,1924 |
0,1984 |
0,2377 |
0,2003 |
|
13 |
0,1768 |
0,1986 |
0,2241 |
0,2022 |
|
14 |
0,1923 |
0,1876 |
0,1903 |
0,1986 |
|
15 |
0,1924 |
0,1996 |
0,2120 |
0,2160 |
|
16 |
0,1720 |
0,1940 |
0,2116 |
0,2320 |
|
17 |
0,1824 |
0,1790 |
0,1876 |
0,1821 |
|
18 |
0,1812 |
0,1585 |
0,1699 |
0,1680 |
|
19 |
0,1700 |
0,1567 |
0,1694 |
0,1702 |
|
20 |
0,1698 |
0,1664 |
0,1700 |
0,1600 |
Оцените статистическую управляемость процесса и предложите свои рекомендации по качеству его настройки и разбросу.
Для исследования коррозии цинка образцы, изготовленные в различных условиях, были подвергнуты климатическим воздействиям. В таблице 11.5 приведены результаты измерений десяти серий по шесть образцов в каждой. Точность измерения 0,0001 дюйм.
Таблица 11.5 Результаты исследований коррозии цинка
|
№ п/п |
Измеренное значение | |||||
|
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
Х6 | |
|
1 |
0,5005 |
0,5000 |
0,5008 |
0,5000 |
0,5005 |
0,5000 |
|
2 |
0,4998 |
0,4997 |
0,4998 |
0,4994 |
0,4999 |
0,4998 |
|
3 |
0,4995 |
0,4995 |
0,4995 |
0,4995 |
0,4995 |
0,4996 |
|
4 |
0,4998 |
0,5005 |
0,5005 |
0,5002 |
0,5003 |
0,5004 |
|
5 |
0,5000 |
0,5005 |
0,5008 |
0,5007 |
0,5008 |
0,5010 |
|
6 |
0,5008 |
0,5008 |
0,5010 |
0,5005 |
0,5006 |
0,5009 |
|
7 |
0,5000 |
0,5001 |
0,5002 |
0,4995 |
0,4996 |
0,4997 |
|
8 |
0,4993 |
0,4994 |
0,4999 |
0,4996 |
0,4996 |
0,4997 |
|
9 |
0,4995 |
0,4995 |
0,4997 |
0,4992 |
0,4995 |
0,4992 |
|
10 |
0,4994 |
0,4998 |
0,5000 |
0,4990 |
0,5000 |
0,5000 |
Оцените результаты
анализа на коррозию с помощью
![]() ,R
карт.
,R
карт.
Контролировались защитные кожухи зубчатой передачи с гальваническим покрытием. Браковочным показателем являлись такие дефекты, как оголенные участки, грубое покрытие и т.п. Объем выборок был постоянным и равнялся 400. Результаты контроля выборок из 15 последовательно взятых партий представлены в таблице 11.6.
Таблица 11.6 – Результаты контроля защитных кожухов
|
№ партии |
Число дефектных изделий |
№ партии |
Число дефектных изделий |
№ партии |
Число дефектных изделий |
|
1 |
1 |
6 |
0 |
11 |
2 |
|
2 |
3 |
7 |
1 |
12 |
0 |
|
3 |
0 |
8 |
0 |
13 |
1 |
|
4 |
7 |
9 |
8 |
14 |
0 |
|
5 |
2 |
10 |
5 |
15 |
3 |
Построить р-карту и оценить статистическую управляемость процесса.
Ежедневно в течении 10 рабочих дней качество продукции контролируется по выборкам размером в 50 единиц. При этом получены следующие результаты (таблица 11.7).
Таблица 11.7 – Результаты контроля продукции
|
День |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Число бракованных изделий |
9 |
7 |
4 |
2 |
4 |
15 |
2 |
3 |
5 |
5 |
Постройте np-карту и проанализируйте статистическую управляемость процесса.
В таблице 11.8 приведены результаты контроля 25 последовательных партий холщовых мешков. Объем выборок был принят равным 10. Подсчитывались все дефекты, даже если встречались два или более одинаковых.
Таблица 11.8 – Результаты контроля холщовых мешков
|
№ выборки |
Число дефектов |
№ выборки |
Число дефектов |
№ выборки |
Число дефектов |
|
1 |
17 |
10 |
18 |
19 |
23 |
|
2 |
14 |
11 |
25 |
20 |
22 |
|
3 |
6 |
12 |
5 |
21 |
9 |
|
4 |
23 |
13 |
8 |
22 |
15 |
|
5 |
5 |
14 |
11 |
23 |
20 |
|
6 |
7 |
15 |
18 |
24 |
6 |
|
7 |
10 |
16 |
13 |
25 |
24 |
|
8 |
19 |
17 |
22 |
|
|
|
9 |
29 |
18 |
6 |
|
|
Построить с-карту и оценить статистическую управляемость процесса.
На заводе по производству шин каждые полчаса контролировали 15 шин и записывали обнаруженное число несоответствий (таблица 11.9).
Таблица 11.9 – Число несоответствий при контроле шин
|
№ выборки |
Число несоответствий с |
№ выборки |
Число несоответствий с |
№ выборки |
Число несоответствий с |
|
1 |
4 |
6 |
1 |
11 |
7 |
|
2 |
5 |
7 |
5 |
12 |
5 |
|
3 |
3 |
8 |
6 |
13 |
2 |
|
4 |
6 |
9 |
2 |
14 |
3 |
|
5 |
2 |
10 |
4 |
|
|
Построить u-карту и оценить статистическую управляемость процесса.
Данные таблицы 11.10 представляют собой количество пробоев провода с резиновой изоляцией, измеряемого последовательными отрезками длиной 10000 см, при заданном испытательном напряжении.
Таблица 11.10 – Количество пробоев в двадцати последовательных отрезках провода длиной по 10000 см
-
№
отрезка
Число пробоев,
с
№
отрезка
Число пробоев, с
№
отрезка
Число пробоев, с
1
1
8
6
15
16
2
1
9
1
16
20
3
3
10
1
17
1
4
7
11
10
18
6
5
8
12
5
19
12
6
1
13
0
20
4
7
2
14
19
При помощи контрольной с-карты оцените статистическую управляемость процесса изготовления провода. Если процесс статистически неуправляем, выполните корректирующие мероприятия и перестройте с-карту.
При контроле процесса нанесения цинкового покрытия на листовое железо средний вес цинкового покрытия определялся по результатам 25 выборок объемом n = 5, извлекаемых из текущей продукции ежедневно. Результаты расчета средних весов покрытий в каждой из выборок приведены в таблице 11.11.
Таблица 11.11 – Результаты измерения веса цинкового покрытия
|
№ выборки |
Средний вес покрытия в выборке, г |
№ выборки |
Средний вес покрытия в выборке, г |
№ выборки |
Средний вес покрытия в выборке, г |
|
1 |
1,47 |
10 |
1,70 |
19 |
1,57 |
|
2 |
1,52 |
11 |
1,60 |
20 |
1,56 |
|
3 |
1,55 |
12 |
1,51 |
21 |
1,65 |
|
4 |
1,38 |
13 |
1,32 |
22 |
1,53 |
|
5 |
1,64 |
14 |
1,47 |
23 |
1,34 |
|
6 |
1,63 |
15 |
1,45 |
24 |
1,43 |
|
7 |
1,53 |
16 |
1,44 |
25 |
1,54 |
|
8 |
1,60 |
17 |
1,48 |
|
|
|
9 |
1,32 |
18 |
1,55 |
|
|
Номинальным
значением цинкового покрытия считается
1,5 г. Оцените особенности протекания
процесса по
![]() -карте
и кусумм-карте. Сравните результаты
оценок.
-карте
и кусумм-карте. Сравните результаты
оценок.
В таблице 11.12 приведены результаты текущего технического контроля хода технологического процесса и указаны числа дефектных изделий в 25 – последовательных выборках объемом 100, извлеченных из готовой продукции. Приемочный уровень качества – допустимое число дефектных изделий в выборке для данного технологического процесса k = 2 (стандартное значение задано).
Таблица 11.12 – Число дефектных изделий в выборках объемом n=100
|
№ выборки |
Число дефектных изделий |
№ выборки |
Число дефектных изделий |
№ выборки |
Число дефектных изделий |
|
1 |
1 |
10 |
1 |
19 |
1 |
|
2 |
2 |
11 |
0 |
20 |
1 |
|
3 |
3 |
12 |
1 |
21 |
4 |
|
4 |
0 |
13 |
1 |
22 |
4 |
|
5 |
1 |
14 |
3 |
23 |
4 |
|
6 |
0 |
15 |
0 |
24 |
0 |
|
7 |
0 |
16 |
3 |
25 |
2 |
|
8 |
0 |
17 |
3 |
|
|
|
9 |
2 |
18 |
4 |
|
|
Оцените особенности
процесса используя
![]() -карты
и кусумм-карты. Сравните результаты
оценок.
-карты
и кусумм-карты. Сравните результаты
оценок.
ЗАКЛЮЧЕНИЕ
Данные о параметрах процессов и характеристиках качества отличаются рассеиванием и имеют, поэтому статистический характер. Для их сбора, анализа и оценки необходимо знание основ теории вероятности и математической статистики, знание основных особенностей и закономерностей распределения случайных событий и величин, способов описания этих распределений.
Основной, в настоящее время, инструмент оценки управляемости процессов – контрольные карты – построен с учетом статистических закономерностей и характеристик распределения измеряемых параметров, их изменчивости. Знание теоретических основ построения и интерпретации контрольных карт является основой творческого подхода к их использованию. То же самое можно сказать и о теории и практике применения планов контроля для контроля качества.
Назначение данного учебного пособия, по замыслу авторов, дать будущим и настоящим инженерам менеджерам, специалистам по управлению качеством запас теоретических знаний и практических навыков для успешного, творческого применения статистических методов управления качеством в их практической деятельности, а также запас знаний и умений для их дальнейшего совершенствования на основе самообразования.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Строителев В.Н. Статистические методы в управлении качеством: учеб. пособие / В.Н. Строителев, В.Е. Яницкий. – М. : Европейский центр по качеству, 2002. – 164 с.
Шор Е.Б. Статистические методы анализа и контроля качества и надежности / Е.Б. Шор. – М. : Советское радио, 1962. – 552 с.
Управление качеством электронных средств: учебник / О.П. Глудкин [и др.]. – М. : Высш. шк., 1994. – 414 с.
Шиндровский Э. Статистические методы управления качеством. Контрольные карты и планы контроля: пер. с нем. / Э. Шиндровский, О. Шюрц. – М. : Мир, 1976. – 597 с.
Статистические методы повышения качества / под ред. Хитоси Кумэ. – М. : Финансы и статистика, 1990. – 214 с.
Исикава К. Японские методы управления качеством: сокр. пер. с англ. / К. Исикава; науч. ред. и авт. предисл. А.В. Гличев. – М. : Экономика. 1988. – 282 с.
Хэнсен Бертран Л. Контроль качества. Теория и применение: пер. с англ. / Бертран Л. Хэнсен; под ред. А.К. Шубникова. М. : Прогресс, 1968. – 520 с.
Коуден Д. Статистические методы контроля качества: пер. с англ. / Д. Коуден; под ред. Б.Р. Левина. – М. : ГИФМЛ, 1961. – 624 с.
Шторм Р. Теория вероятностей. Математическая статистика. Статистический контроль качества продукции: пер. с нем. / Р. Шторм; под ред. Н С. Райбмана. – М. : Мир, 1970. – 366 с.
ГОСТ Р 50779.71-99 (ИСО 2859.1 – 89) Процедуры выборочного контроля по альтернативному признаку. Часть 1. Планы выборочного контроля последовательных партий на основе приемлемого уровня качества AQL. – Введ. 01.07.2000. – М. : Изд-во стандартов, 2000. – 70 с.
ГОСТ Р 50779.72-99 (ИСО 2859.2 – 89) Процедуры выборочного контроля по альтернативному признаку. Часть 2. Планы выборочного контроля отдельных партий на основе предельного уровня качества LQ. – Введ. 01.07.2000. – М. : Изд-во стандартов, 2000. – 28 с.
ГОСТ Р 50779.74 (ИСО 3951 – 89) Процедуры выборочного контроля и карты контроля по количественному признаку для процента несоответствующих единиц продукции. – Введ. 01.07.2000. – М. : Изд-во стандартов, 2000. – 105 с.
ГОСТ Р 50779.40-96 (ИСО 7870 – 93) Статистические методы. Контрольные карты. Общее руководство и введение. – Введ. 01.07.1997. – М. : Изд-во стандартов, 1996. – 20 с.
ГОСТ Р 50779.42-99 (ИСО 8258 – 91) Статистические методы. Контрольные карты Шухарта. – Введ. 01.01.2000. – М. : Изд-во стандартов, 1999. – 32 с.
ГОСТ Р 50779.41-96 (ИСО 7873 – 93) Статистические методы. Контрольные карты для арифметического среднего с предупреждающими границами. – Введ. 01.07.1997. – М. : Изд-во стандартов, 1996. – 24 с.
ГОСТ Р 50779.43-99 (ИСО 7966 – 93) Статистические методы. Приемочные контрольные карты. – Введ. 01.07.2000. – М. : Изд-во стандартов, 2000. – 24 с.
Shewhart W. Economic Control Manufactured Product / W. Shewhart. – Miltwaukee, WI : ASQ Quality Press, 1931, (reprint 1980). – 501 p.










 1
1