
[ Будылин ] Лекции по математике. 3 семестр
.pdf
Лекции по математике, III семестр
А.М.Будылин
budylin@mph.phys.spbu.ru
16 декабря 2001 г.
Кратные интегралы Интегралы на многообразиях Приложения
Предметный указатель Литература
Веб – страница
Титульный лист
JJ II
J I
Страница 1 из 245
Назад
Полный экран
Закрыть
Выход

Часть I
Кратные интегралы
Содержание
1.Определение и свойства кратных интегралов
1.1Введение. Двойные и тройные интегралы — интуитивный подход
1.2Интеграл по n-мерному интервалу
1.3Свойства интеграла
2.Интегрируемые функции
2.1Множества объема-ноль
2.2Множества меры-ноль
2.3Измеримые множества и интегралы по ним
3.Теорема Фубини
3.1Сведение кратного интеграла к повторному
3.2Некоторые приложения
3.2.1Вычисление кратных интегралов
3.2.2Объем цилиндрического тела
3.2.3Принцип Кавальери
3.2.4Равенство непрерывных смешанных производных
4.Аддитивные функции
Кратные интегралы
Интегралы на многообразиях Приложения
Предметный указатель Литература
Веб – страница
Титульный лист
JJ II
J I
Страница 2 из 245
Назад
Полный экран
Закрыть
Выход

4.1Плотность аддитивной функции
4.2Коэффициент искажения объема
5.Замена переменных в интеграле
5.1Предварительное замечание
5.2Коэффициент искажения объема в случае линейных отображений
5.2.1Экскурс в линейную алгебру
5.2.2Коэффициент искажения
5.3Коэффициент искажения объема при непрерывно дифференцируемом отображении
5.3.1Экскурс в дифференциальное исчисление функций нескольких переменных
5.3.2Лемма о трех концентрических кубах
5.3.3Замена переменных в кратном интеграле
5.3.4Примеры
6.Несобственные интегралы
6.1Абсолютно интегрируемые функции
6.2Положительные абсолютно интегрируемые функции
6.3Абсолютная интегрируемость функций
6.4Интеграл Пуассона. Объем единичного шара
7.Предельный переход под знаком интеграла
Кратные интегралы
Интегралы на многообразиях Приложения
Предметный указатель Литература
Веб – страница
Титульный лист
JJ II
J I
Страница 3 из 245
Назад
Полный экран
Закрыть
Выход

1.Определение и свойства кратных интегралов
1.1.Введение. Двойные и тройные интегралы — интуитивный подход
Пусть D — область |
на плоскости. Разобьем ее на непересекающиеся подобласти |
D1, D2, . . . Dn |
n |
|
k[ |
|
D = Dk , Di ∩ Dj = (i 6= j) . |
|
=1 |
Совокупность этих подобластей назовем разбиением области D и обозначим через λ:
D
Рис. 1: Разбиение области
Кратные интегралы Интегралы на многообразиях
Приложения
Предметный указатель
Литература
Веб – страница
Титульный лист
JJ II
J I
Страница 4 из 245
Назад
Полный экран
Закрыть
Выход

λ = {D1, . . . Dn} .
Диаметром области D называется расстояние между наиболее удаленными одна от другой точками области D, точнее
diam D = sup |P Q| .
P,QD
(Очевидно, это — диаметр круга, описанного около данной области). Наибольший из
D
diam D
Рис. 2: Диаметр области
диаметров подобластей Di разбиения λ называется рангом разбиения |λ|:
|λ| = max Di .
16i6n
Пусть f : D → R — вещественнозначная функция, определенная на области D. Выберем в каждой подобласти Di разбиения λ точку Pi и составим интегральную сумму Римана
n |
|
Xi |
(1.1) |
s(f, Λ) = f(Pi)S(Di) , Pi Di . |
|
=1 |
|
Здесь S(Di) — площадь области Di и Λ = {(D1, P1), . . . (Dn, Pn)}. Последний символ (так сказать — «нагруженное» разбиение) зависит как от разбиения λ, так и от выбора точек дробления Pi.
Кратные интегралы Интегралы на многообразиях
Приложения
Предметный указатель Литература
Веб – страница
Титульный лист
JJ II
J I
Страница 5 из 245
Назад
Полный экран
Закрыть
Выход

Если существует предел интегральных сумм при ранге разбиения стремящемся к нулю, он называется двойным интегралом от функции f по области D и обозначается
|
ZZ f dS = |λ|→0 |
|
|
|
|
lim s(f, Λ) . |
|
|
|
|
D |
|
|
|
Уточним, что это означает: |
|λ| < δ s(f, Λ) − ZZ |
|
||
ε > 0 δ > 0 : |
f dS < ε |
|||
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
при любом выборе точек Pi Di.
Как и в случае однократного интеграла, очевидно, такой предел может существовать лишь если функция f ограничена:
sup |f(P )| = M < ∞ .
P D
Аналогичные построения можно провести и в случае трехмерной области, естественно заменяя термин «площадь» на термин «объем». При этом получим тройной интеграл от функции f по области D R3
ZZZ |
|
n |
= |λ|→0 |
i=1 f(Pi)V (Di) , |
|
D |
lim s(f, Λ) , |
X |
f dV |
s(f, Λ) = |
V (Di) — объем области Di.
Как и в одномерном случае мы должны задаться вопросами существования таких интегралов, а также описать свойства этих интегралов. Однако в отличие от теории определенного (однократного) интеграла мы сталкиваемся с рядом новых вопросов, которых по существу не было ранее. Именно:
Кратные интегралы
Интегралы на многообразиях Приложения
Предметный указатель Литература
Веб – страница
Титульный лист
JJ II
J I
Страница 6 из 245
Назад
Полный экран
Закрыть
Выход

1.Какие множества (на плоскости или в пространстве, соответственно) можно брать для построения кратного интеграла?
2.Какие подмножества допустимы при разбиениях?
3.Что такое площадь или объем, соответственно?
Эти вопросы, в действительности, весьма трудны и неоднозначны. Чтобы дать представление о возникающих на этом пути трудностях, коснемся понятий площади и объема.
Под площадью S мы понимаем неотрицательную функцию S(D) > 0, определенную на плоских множествах D такую, что
1.Площадь прямоугольника со сторонами длины a и b равна произведению ab,
2.S(D1 D2) = S(D1) + S(D2) если множества D1 и D2 не пересекаются,
3.Площадь множества не меняется при его жестком перемещении (конгруэнтные фигуры имеют равные площади).
Аналогично, под объемом V мы понимаем неотрицательную функцию V (D) > 0, определенную на множествах D R3 такую, что
1.Объем прямоугольного параллелепипеда с ребрами длины a, b и c равна произведению abc,
2.V (D1 D2) = V (D1) + V (D2), если множества D1 и D2 не пересекаются,
3.Объем множества не меняется при его жестком перемещении (конгруэнтные тела имеют равные объемы).
Параллели, казалось бы, очевидны. При этом, однако, доказано (С.Банах), что площадь существует, хотя и не единственна, т.е. существуем много разных функций S, определенных на произвольных плоских множествах и удовлетворяющих описанным выше свойствам. Все эти функции для сравнительно простых множеств показывают одно и
Кратные интегралы
Интегралы на многообразиях
Приложения Предметный указатель Литература
Веб – страница
Титульный лист
JJ II
J I
Страница 7 из 245
Назад
Полный экран
Закрыть
Выход

то же значение площади, однако для множеств сложной структуры ответы оказываются разными. Вместе с тем объема не существует вовсе (Ф.Хаусдорф), т.е. не существует такой функции V , удовлетворяющей описанным выше свойствам и определенной для всех множеств в пространстве.
Интересно, что столь разные ответы на вопрос о существовании и единственности понятия меры (площади или объема) множеств приводят к одному и тому же заключению: не следует пытаться наделить мерой произвольные множества. Надо довольствоваться только достаточно «хорошими» множествами, для которых понятие площади или, соответственно, объема существует и определено однозначно. Однако вопрос о том, что же такое эти «хорошие» множества решается, по-существу, в рамках построения теории (кратного) интеграла.
Мы начнем изложение строгой теории кратных интегралов для самых простых областей — прямоугольных параллелепипедов. Это позволит, кстати, строить теорию совершенно параллельно со случаем однократного определенного интеграла.
1.2.Интеграл по n-мерному интервалу
Определение 1.1. Замкнутый прямоугольный параллелепипед или n-мерный интервал
D Rn определен условием
P (x1, . . . xn) D ai 6 xi 6 bi , i = 1, . . . n .
При этом пишут
D= [a1, b1] × . . . × [an, bn] .
Вдальнейшем такие параллелепипеды будем называть брусами. Объем V (D) бруса определим равенством
n |
|
Опр. |
|
iY |
(1.2) |
V (D) = (bi − ai) = (b1 − a1) · . . . · (bn − an) . |
|
=1 |
|
Кратные интегралы Интегралы на многообразиях
Приложения Предметный указатель Литература
Веб – страница
Титульный лист
JJ II
J I
Страница 8 из 245
Назад
Полный экран
Закрыть
Выход

Напомним, что разбиением λ интервала [a, b] удобно называть множество точек
{t0, t1, . . . , tk} таких, что
a = t0 < t1 < . . . < tk = b .
Множество λ действительно делит интервал [a, b] на k интервалов [ti−1, ti] , i = 1, . . . k.
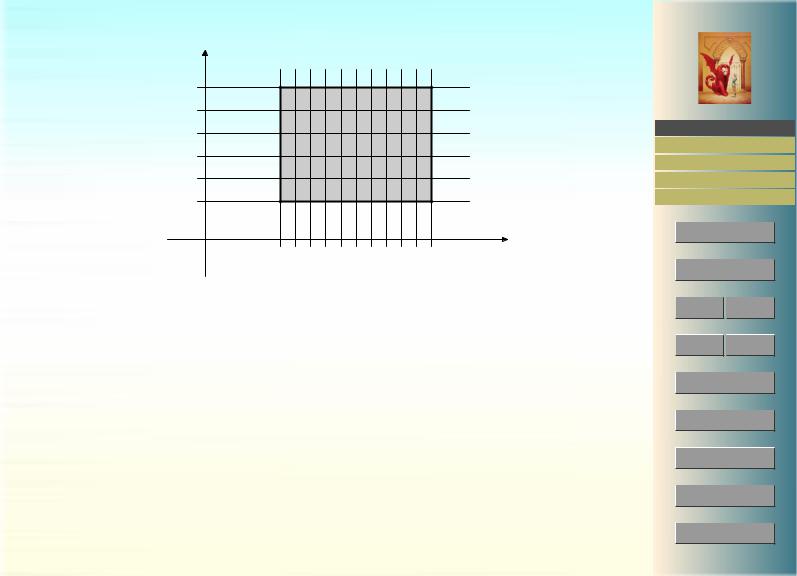
Определение 1.2. Разбиением λ бруса D называется кортеж1 λ = (λ1, . . . λn) одномерных разбиений λi интервалов [ai, bi].
Пусть, например, λ1 = {t0, . . . tk} — разбиение интервала [a1, b1] и λ2 = {s0, . . . sm} — разбиение интервала [a2, b2]. Тогда разбиение λ = (λ1, λ2) прямоугольника [a1, b1]×[a2, b2] делит его на k · m прямоугольников [ti−1, ti] × [sj−1, sj].
Вообще, если λ = (λ1, . . . λn) —разбиение бруса D = [a1, b1]×. . .×[an, bn] и разбиение λi делит интервал [ai, bi] на ki частей, то брус D делится на k1 ·k2 ·. . .·kn частей (брусы– ячейки). Допуская определенную вольность речи, мы будем в дальнейшем о данных ячейках говорить как о параллелепипедах (ячейках, брусах) из разбиения λ.
Пусть f : D → R — ограниченная функция:
sup |f(P )| = M < ∞ .
P D |
|
|
Для каждого множества A D положим |
|
|
MA(f) = sup f(P ) , |
mA(f) = inf f(P ) . |
(1.3) |
P A |
P A |
|
Разность |
|
|
ωA(f) = MA(f) − mA(f) |
(1.4) |
|
называется колебанием функции f на множестве A.
1кортеж - это упорядоченный набор элементов
Кратные интегралы
Интегралы на многообразиях Приложения Предметный указатель
Литература
Веб – страница
Титульный лист
JJ II
J I
Страница 9 из 245
Назад
Полный экран
Закрыть
Выход
b2 |
|
|
|
Кратные интегралы |
|
|
Интегралы на многообразиях |
|
|
Приложения |
|
|
Предметный указатель |
|
a2 |
Литература |
|
|
|
|
a1 |
Веб – страница |
|
b1 |
|
|
|
Титульный лист |
|
Рис. 3: К определению 1.2 |
JJ |
II |
|
|
|
Определение 1.3. Пусть λ — разбиение бруса D и f : D → R — ограниченная функция. Верхняя и нижняя суммы Дарбу определяются, соответственно, равенствами
|
X |
X |
σ (f, λ) = |
MA(f)V (A) , σ (f, λ) = |
mA(f)V (A) , |
|
по A из λ |
по A из λ |
суммирование ведется по всем параллелепипедам A из разбиения λ.
По построению, очевидно,
σ (f, λ) 6 σ (f, λ) .
Более того.
J I
Страница 10 из 245
Назад
Полный экран
Закрыть
Выход
