[ Будылин ] Ряды и интегралы Фурье

7.2. Распространение тепла в бесконечном стержне

Рассмотрим задачу о распространении тепла в бесконечном стержне, если задана начальная температура u(x, 0) = ϕ(x). Эту задачу принято называть задачей Коши для уравнения теплопроводности

	∂u	= a2	∂2u	, x	R, t [0, +∞) ,
	∂t		∂x2
u(x, 0) = ϕ(x) , x						R.

Фиксируя t, подвергнем функцию u(x, t) преобразованию Фурье:

U(ξ, t) = (F u)(ξ, t) .

Тогда рассматриваемая задача Коши будет иметь следующий образ Фурье:

∂t = −a2		ξ2U,	ξ R, t [0, +∞) ,
	∂U
	U(ξ, 0) = Φ(ξ) ,		ξ		R.

Здесь Φ = F ϕ. Фиксируя ξ, решим полученное дифференциальное уравнение:

U(ξ, t) = Φ(ξ)e−a2ξ2t .

Решение исходной задачи находится по формуле

u(x, t) = (F −1U)(x, t) .

Здесь полезно воспользоваться теоремой о свертке в форме 6.2:

F [e−a2ξ2t] ϕ = F (e−a2ξ2t · F ϕ) .

Ряды Фурье

Интегралы Фурье

Предметный указатель Литература

Веб – страница

Титульный лист

JJ II

J I

Страница 111 из 127

Назад

Полный экран

Закрыть

Выход

Заметим, что в силу четности (по ξ) и теоремы подобия (роль множителя играет

√

a t)

2	2	2 2			1		e−	x2
F [e−a	ξ	t] = F [e−a ξ	t] =		√			4a2t	.
				a		2t

(Здесь также поменялись ролями переменные x и ξ). Тогда

	1		+∞		(x−y)2
u(x, t) =	2a√		Z	ϕ(y)e−		dy .
					4a2t
		πt

−∞

Отметим, что в отличие от волнового уравнения, параметр a не играет роль скорости распространения тепла. Как видно из полученного решения, скорость распространения тепла бесконечна (с точки зрения данной модели): в любой сколь угодно малый момент времени t > 0 изменение температуры u(x, t) происходит на всем протяжении бесконечного стержня (для всех x)!

7.3. Частотный спектр

В связи с предельным переходом, описанным в параграфе 5.1, полезно познакомиться с понятием частотного спектра.

Пусть f — вещественная периодическая функция с периодом 2l. Ее разложение в ряд Фурье имеет вид

∞

f(x) = a20 + X(an cos ωnx + bn sin ωnx) ,

n=1

где

πn ωn = l .

Величины ωn имеют смысл частот колебаний и называются гармониками, причем гармоника ω1 называется основной частотой, остальные гармоники ωn = nω1, кратные основной, называются обертонами.

Ряды Фурье

Интегралы Фурье

Предметный указатель

Литература

Веб – страница

Титульный лист

JJ II

J I

Страница 112 из 127

Назад

Полный экран

Закрыть

Выход

Введем величины
	a0
A0 =					= pan2 + bn2 , n > 1 .
		,	An
	2
Разложение в ряд Фурье может быть переписано в виде
			X
f(x) A0 +					An sin(ωnx + ϕn) ,
			n=1
где фазы колебаний ϕn определяются равенствами
sin ϕn =			an	,	cos ϕn =			bn	.
			An					An

Последовательность амплитуд колебаний An, отнесенных к соответствующим гармоникам, и носит название дискретного частотного спектра.

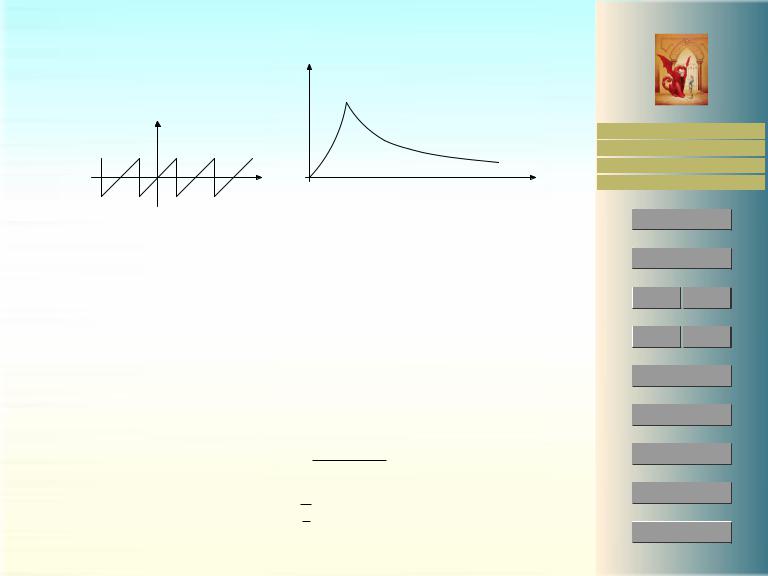
Найдем, например, частотный спектр пилообразной 2l-периодической функции, заданной на периоде равенством

f(x) = x , x [−l, l] .

Ее разложение в ряд Фурье имеет вид

X

+∞ (−1)n+12l

f(x) = sin ωnx , πn

n=1

откуда

2l An = πn ,

см. рис. 5.

Следует подчеркнуть, что частотный спектр не определяет функцию f(x) однозначно.

Ряды Фурье

Интегралы Фурье

Предметный указатель

Литература

Веб – страница

Титульный лист

JJ II

J I

Страница 113 из 127

Назад

Полный экран

Закрыть

Выход

		An
f(x)
								Ряды Фурье
								Интегралы Фурье
0	l							Предметный указатель
		0
	x		ω1	ω2	ω3	ω4	ωn	Литература
	Рис. 5: Дискретный частотный спектр							Веб – страница
								Титульный лист

Совершая предельный переход l → ∞, мы получаем интеграл Фурье функции f(x):

			∞
		f(x) = Z0		[a(ξ) cos ξx + b(ξ) sin ξx] dξ ,
где		+∞					+∞
a(ξ) = π					b(ξ) = π
		Z	f(x) cos xξ dx ,				Z f(x) sin xξ dx .
1					1
		−∞					−∞

По аналогии с дискретным случаем, вводится непрерывный частотный спектр

p

A(ξ) = a2(ξ) + b2(ξ) .

Заметим, что

r

fb(ξ) = π2 · [a(ξ) − ib(ξ)] ,

JJ II

J I

Страница 114 из 127

Назад

Полный экран

Закрыть

Выход

откуда

A(ξ) = r

π

· |f(ξ)| .

2

b

Величина

A(ξ)

служит мерой вклада частоты ξ в функцию f(x).

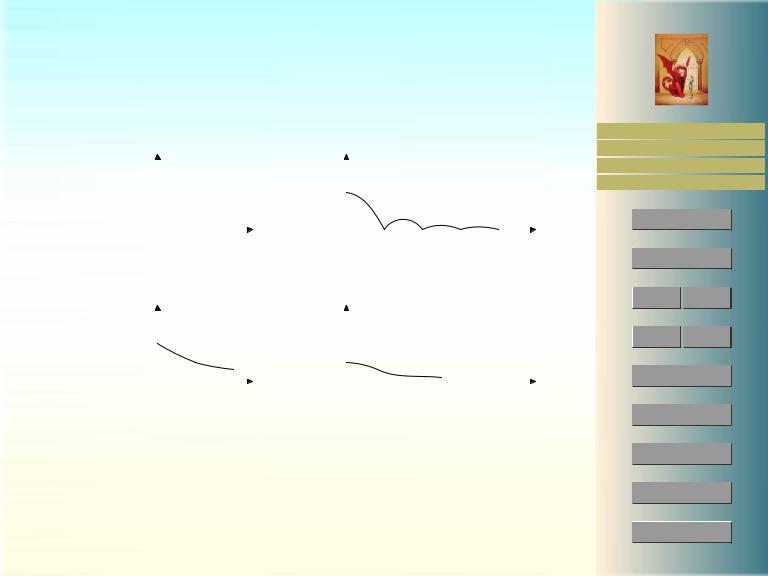
На рисунке 6 можно видеть примеры непрерывных частотных спектров.

f(x)

A(ξ) = π ·

ξ

2

sin ξ

0

1

x

0

π

ξ

f(x) = e−xH(x)

A(ξ) =

1

1

·

π

p

0

0

1 + ξ2

x

ξ

Рис. 6: Примеры непрерывных частотных спектров

Ряды Фурье

Интегралы Фурье

Предметный указатель

Литература

Веб – страница

Титульный лист

JJ II

J I

Страница 115 из 127

Назад

Полный экран

Закрыть

Выход

A.Дополнение. Сходимость в среднеквадратичном

Мы докажем в этом параграфе, что для произвольной кусочно непрерывной и квадратично интегрируемой функции f интеграл

fN (x) =	+∞			+∞				dt ,
	Z	f(t)DN (x − t) dt = π		Z	f(t) x − t−
		1				sin N(x	t)
	−∞			−∞

называемый простым интегралом Фурье функции f, в среднеквадратичном сходится к функции f, т.е.

								= v
k	f	−	fN	k N→	0 ,	f	k		+∞ f(x)	2 dx .
						k		u	| |
				→∞				u	Z

			u−∞
Если определить функцию	√		t
	DN (x) =	2π	DN (x) ,
то интеграл fN (x) можно записать как свертку
	fN (x) = f DN (x) .

Введем срезающий оператор N . Если f — произвольная функция на оси, то

	N		(0 ,	x / [ N, N] .
		f(x) =	g(x) , x [−N, N] ,

−

Тогда, если преобразование Фурье fb = F f функции f существует и как несобственный интеграл сходится равномерно, то простой интеграл Фурье запишется в

виде

fN = F N F f .

Нам будут полезны следующие две леммы.

Ряды Фурье

Интегралы Фурье Предметный указатель

Литература

Веб – страница

Титульный лист

JJ II

J I

Страница 116 из 127

Назад

Полный экран

Закрыть

Выход

Лемма A.1 (Интегральное неравенство Минковского). Пусть функция f(x, y)

непрерывна. Тогда

v

d dyv

b dx

d f(x, y) dy

2 6

b

|

f(x, y)

2 dx .

u

Z

Z

u

|

uZ

uZ

u

u

t

t

a

c

c

a

(Пределы интегрирования могут быть бесконечными).

Доказательство. Положим

d

Z

g(x) = f(x, y) dy .

				c
По неравенству Шварца
			v					v
Z	b		u b					u b
			Z						Z
			u					u		|g(x)|2 dx .
a	|f(x, y)g(x)| dx 6 ua				|f(x, y)|2 dx ua
Заметим, что			t					t
			f(x, y) dy 2
	b	d				= Z	b
	Z	dx Z					|g(x)|2 dx .
	a	c				a

Ряды Фурье

Интегралы Фурье Предметный указатель Литература

Веб – страница

Титульный лист

JJ II

J I

Страница 117 из 127

Назад

Полный экран

Закрыть

Выход

При этом

b

b

d

Za

|g(x)|2 dx 6 Za

dx|g(x)| Zc

|f(x, y)| dy

d dyv

v

=

d dy

b

f(x, y)g(x)

dx 6

b

f(x, y)

2 dx

b

g(x) 2 dx ,

Zc

|

|

Zc

u

|

|

u

|

|

Za

uZa

uZa

u

u

t

t

откуда

vv

u b	d	u b
Z	Z	Z

uu

ua	|g(x)|2 dx 6 c	dyua	|f(x, y)|2 dx ,
t		t

что и требовалось доказать.

Лемма A.2 (Равенство Парсеваля). Пусть f — финитная непрерывная (кусочно– непрерывная) функция и fb — ее преобразование Фурье. Тогда

kfbk = kfk ,

т.е.

+∞

+∞

ZZ

|fb(ξ)|2 dξ = |f(x)|2 dx .

−∞ −∞

Доказательство. Напомним, что функция называется финитной, если она обращается в ноль на внешности некоторого интервала. Предположим вначале, что f(x) обращается в ноль вне интервала [−π, π]. Переопределим ее как 2π-периодическую,

Ряды Фурье

Интегралы Фурье

Предметный указатель

Литература

Веб – страница

Титульный лист

JJ II

J I

Страница 118 из 127

Назад

Полный экран

Закрыть

Выход

продолжая ее с интервала [−π, π] на всю ось как периодическую. Для разложения таким образом переопределенной функции f(x) в ряд Фурье

+∞				1		π
					Z		f(x)e−inx dx ,
f(x) n=		cneinx ,	cn =
				2π
X					−	π
	−∞

выполняется равенство Парсеваля для рядов:

	π	|f(x)|2 dx = 2π n=∞	|cn|2 .
Z
		+
−		X
	π	−∞

Пусть α [0, 1). Тогда замещая f(x) функцией e−iαxf(x), находим

π

Z

|f(x)|2 dx = 2π

−π

Заметим, что

откуда

+∞

X

|cn(α)|2 ,

n=−∞

fb(n + α) =

				π	f(x)e−i(n+α)x dx .
	cn(α) = 2π Z
1
				−π
√		cn(α) ,
	2π

π	|f(x)|2 dx =	+∞	|f(n + α)|2 .
Z
		X	b

−π n=−∞

Остается проинтегрировать полученное равенство по α в пределах от 0 до 1, замечая, что

1n+1

ZZ

0

|fb(n + α)|2 dα = n

|fb(ξ)|2 dξ .

Ряды Фурье Интегралы Фурье

Предметный указатель Литература

Веб – страница

Титульный лист

JJ II

J I

Страница 119 из 127

Назад

Полный экран

Закрыть

Выход

В силу аддитивности интеграла

	π	+	n+1		+∞
Z		|f(x)|2 dx = n=∞	Z	|f(ξ)|2 dξ = Z		|f(ξ)|2 dξ .
−	π	X		b	−∞	b
		−∞ n

Рассмотрим теперь общий случай, считая, что функция f(x) обращается в ноль вне интервала [−l, l]. Тогда функция g(x) = f(ax), где a = πl , обращается в ноль вне интервала [−π, π] и для нее верно равенство

	+∞			π			+∞
	Z	|g(x)|2 dx = Z				|g(x)|2 dx = Z			|g(ξ)|2 dξ .
−∞			−π				−∞ b
Но			+∞						+∞
+∞
Z		|f(x)|2 dx = Z			f(at) 2a dt = a Z					|g(x)|2 dx
−∞			−∞					−∞
и, согласно теореме подобия,
			g(ξ) = bfb(bξ) ,				1
откуда							b =		,
								a
			b
+∞			+∞					+∞
Z	|f(ξ)|2 dξ = Z			|f(bη)|2b dη = a Z						|g(η)|2 dη .
−∞		b	−∞		b		−∞			b

Перейдем к основному исследованию.

Ряды Фурье Интегралы Фурье Предметный указатель

Литература

Веб – страница

Титульный лист

JJ II

J I

Страница 120 из 127

Назад

Полный экран

Закрыть

Выход