[ Будылин ] Ряды и интегралы Фурье

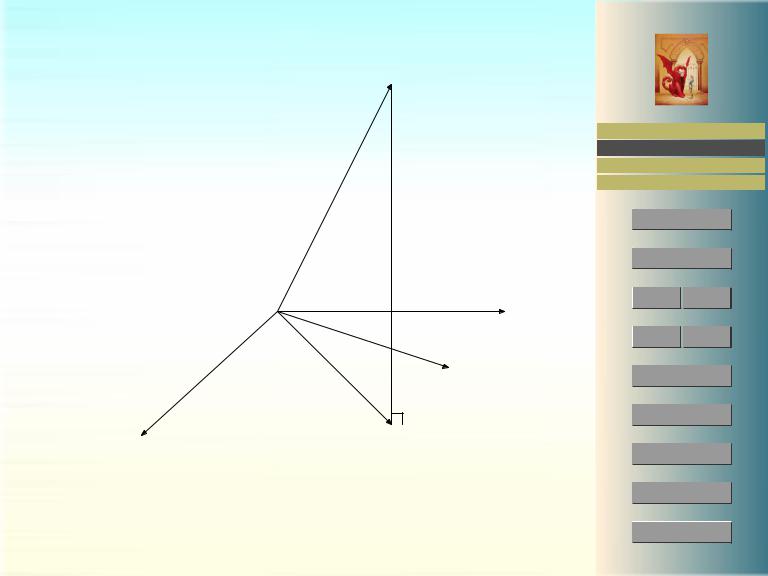
→− a

→− e2

1→−	→−
λ e1	+ λ2 e2

e1	1→−	→−
→−	c e1	+ c2 e2

Рис. 1: Перпендикуляр — наименьшее расстояние до подпространства

Ряды Фурье Интегралы Фурье Предметный указатель Литература

Веб – страница

Титульный лист

JJ II

J I

Страница 21 из 127

Назад

Полный экран

Закрыть

Выход

2.3.Ряды Фурье на пространстве непрерывных 2π−периодических

функций

Очевидно, пространство [комплекснозначных] непрерывных периодических с периодом 2π функций является комплексным векторным пространством: такие функции можно складывать и умножать на комплексные числа не выходя за рамки этого множества функций. Превратим это пространство в унитарное, введя в нем скалярное произведение

	2π	f(x)g(x) dx .			(2.10)
hf|gi = 2π Z0
1

Свойства 1)–3) скалярного произведения очевидны. Четвертое свойство является следствием непрерывности рассматриваемых функций. Действительно, если

	2π	|f(x)|2 dx = 0 ,
kfk2 = 2π Z0
1

то f(x) ≡ 0 именно благодаря своей непрерывности. 6

Обозначим это унитарное пространство [комплекснозначных] непрерывных пе-

периодом

2π

функций через

C2π

. Через

en , n Z,

будем обозначать

риодических с inx

функции x 7→e

. Покажем, что функции en образуют ортонормированную систему

в C2π.

2π

2π

hen|emi = 2π Z0

einxe−imx dx = 2π Z0

ei(n−m)x dx = δnm ,

1

1

см. (1.2).

6 Для разрывных функций такого заключения сделать уже нельзя

Ряды Фурье Интегралы Фурье

Предметный указатель

Литература

Веб – страница

Титульный лист

JJ II

J I

Страница 22 из 127

Назад

Полный экран

Закрыть

Выход

Если f — произвольная непрерывная периодическая с периодом 2π функция, то ее коэффициенты Фурье относительно ортонормированной системы (en) равны

				2π					(2.11)
cn(f) = 2π Z0						f(x)e−inx dx .
		1
Заметим, что в силу леммы Римана-Лебега
	2π
	Z0	f(x)einx dx n→∞→ 0 .
Неравенство Бесселя принимает вид
+∞						1		2π
								Z |f(x)|2 dx ,
n=		|cn|2 6 2π
X
	−∞							0
где cn = cn(f) и
						2π		|f(x)|2 dx ,
	kfk2 = 2π Z0
		1

Далее мы покажем, что для f C2π неравенство Бесселя превращается в равенство

	+∞				1	2π
			|cn|2	=		Z |f(x)|2 dx
	n=				2π
	X
		−∞				0

и называется равенством Парсеваля или уравнением замкнутости.

Ряды Фурье Интегралы Фурье

Предметный указатель

Литература

Веб – страница

Титульный лист

JJ II

J I

Страница 23 из 127

Назад

Полный экран

Закрыть

Выход

Функции вида

n

X

Tn(x) = λkeikx

k=−n

называются тригонометрическими полиномами. Среди всех тригонометрических полиномов степени не выше n наилучшей аппроксимацией (в смысле среднеквадратичной нормы) функции f(x) является частичная сумма ряда Фурье этой функции

n

X

f(x) ≈ ck(f)eikx .

k=−n

2.4.Свертка периодических функций

Определение 2.8. Пусть f и g — произвольные непрерывные периодические с периодом 2π функции. Их сверткой f g называется функция

	2π	f(t)g(x − t) dt , x R.
f g (x) = 2π Z0
1

Очевидно, свертка f g — периодическая с периодом 2π и непрерывная функция:

		1	2π		1	2π
	f g (x + 2π) =		Z0	f(t)g(x + 2π − t) dt =		Z0	f(t)g(x − t) dt = f g (x) ,
		2π			2π

поскольку g периодична. Чтобы показать непрерывность, заметим, что g — равномерно непрерывна, т.е.

ε > 0 δ > 0 : |x2 − x1| < δ |g(x2) − g(x1)| < ε .

Ряды Фурье Интегралы Фурье Предметный указатель

Литература

Веб – страница

Титульный лист

JJ II

J I

Страница 24 из 127

Назад

Полный экран

Закрыть

Выход

Фиксируем

ε > 0

и выберем такое

δ

по числу

ε

, где

max

. Тогда при

|x − x0| < δ

M

M = 06t62π

|f(t)|

2π

|f g (x) − f g (x0)| = 2π Z f(t)[g(x − t) − g(x0 − t)] dt

1

0

2π

6 2π Z0

|f(t)||g(x − t) − g(x0 − t)| dt

1

6 M

2π

|f(t)| dt 6 M · M = ε .

· 2π Z0

ε

1

ε

Теорема 2.9. Пусть f — периодическая с периодом 2π и непрерывная функция. Если функция g является непрерывно дифференцируемой периодической с периодом 2π, то свертка f g также является непрерывно дифференцируемой периодической с периодом 2π и

	2π	f(t)g0(x − t) dt .
(f g)0(x) = 2π Z0
1

Доказательство. Следствие теоремы о дифференцировании интеграла по параметру: в данном случае частная производная подынтегральной функции

∂x∂ [f(t)g(x − t)] = f(t)g0(x − t)

является непрерывной функцией обеих переменных.

Ряды Фурье Интегралы Фурье

Предметный указатель

Литература

Веб – страница

Титульный лист

JJ II

J I

Страница 25 из 127

Назад

Полный экран

Закрыть

Выход

Следствие 2.10. Если g непрерывно дифференцируема k раз, то свертка f g (где f — непрерывна) — тоже k раз непрерывно дифференцируема и

(f g)(k) = f g(k) .

Интересны также следующие свойства свертки.

Теорема 2.11. Свертка функций является билинейной, коммутативной и ассоциативной операцией, т.е.

1.(λf + µg) h = λf h + µg h ,

2.f g = g f ,

3.f (g h) = (f g) h .

Доказательство. Линейность по первому аргументу очевидна в силу линейности интеграла. Линейность по второму аргументу может быть установлена аналогично, но она также является следствием коммутативности. Докажем коммутативность.

		2π	f(t)g(x − t) dt = [x − t = u, dt = −du]
f g (x) = 2π Z0
	1
	= −2π				x−2π		2π		x	g(u)f(x − u) du
					Z	f(x − u)g(u) du =		Z
			1				1
					x			x−2π
									2π
							= 2π Z0			g(u)f(x − u) du = g f (x) .
								1

Ряды Фурье

Интегралы Фурье Предметный указатель Литература

Веб – страница

Титульный лист

JJ II

J I

Страница 26 из 127

Назад

Полный экран

Закрыть

Выход

Докажем теперь ассоциативность.

2π

2π 2π

f(s)g(t − s)h(x − t) dsdt

(f g) h (x) = 2π Z0

f g (t)h(x − t) dt = 4π2

Z0

Z0

1

1

2π

ds f(s)

2π−s

2π

2π

= 4π2 Z

Z

g(u)h(x − s − u) du =

4π2 Z

ds f(s) Z g(u)h(x − s − u) du

1

1

0

−s

2π

0

0

= 2π Z0

f(s)g h (x − s) ds = f (g h) (x) .

1

Для приложений важность понятия свертки определяется следующим свойством, которое также объясняет свойства, описанные в предыдущей теореме.

Теорема 2.12. Пусть f и g — произвольные непрерывные периодические с периодом 2π функции. Тогда

cn(f g) = cn(f) · cn(g) ,

где cn — коэффициент Фурье соответствующей функции относительно ортонормированной системы экспонент en.

Доказательство. Заметим, сначала, что

		1	2π		1	2π
	f en (x) =		Z0	f(t)ein(x−t) dt = einx		Z0	f(t)e−int dt = cn(f)en(x) ,
		2π			2π
	так что			f en = cn(f)en .
							(2.12)

Ряды Фурье

Интегралы Фурье

Предметный указатель

Литература

Веб – страница

Титульный лист

JJ II

J I

Страница 27 из 127

Назад

Полный экран

Закрыть

Выход

Тогда

cn(f g) = (f g) en (0) = f (g en) (0) = f [cn(g)en] (0) = cn(g)f en (0) = cn(g)cn(f) .

В приложениях отображение f 7→f g описывает прохождение сигнала f через фильтр g. В результате амплитуда cn(f) n-ой гармоники сигнала умножается на cn(g). Заметим, что в силу теоремы Римана-Лебега, не может существовать идеального фильтра, не искажающего сигнал:

6 g : f g = f .

Но вернемся к теореме 2.9. Она позволяет установить одно важное для дальнейшего свойство.

Обозначим через C21π множество непрерывно дифференцируемых периодических с периодом 2π функций. Это подмножество в C2π.

Теорема 2.13 (Плотность C1	в C	2π	). Множество функций C1 плотно в C		2π	,
2π				2π
т.е. f C2π и ε > 0 g C21π:
	def	max		|f(x) − g(x)| < ε .
kf − gk∞ =		06x62π
Доказательство. Функция f — равномерно непрерывна и, следовательно, для
ε > 0 δ > 0 :	|x2 − x1| < δ |f(x2) − f(x1)| < ε .

Пусть ε > 0 фиксировано и δ найдено. Возьмем произвольно функцию ω C21π, удовлетворяющую следующим условиям:

1. ω(x) > 0 ,

Ряды Фурье

Интегралы Фурье Предметный указатель Литература

Веб – страница

Титульный лист

JJ II

J I

Страница 28 из 127

Назад

Полный экран

Закрыть

Выход

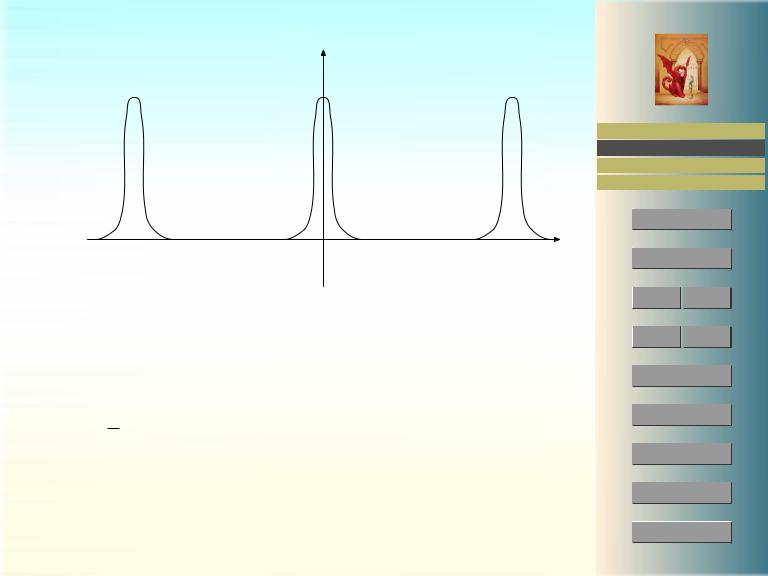
−2π	0	δ	2π

Рис. 2: Сглаживающая функция

2.ω — четная функция,

3.ω(x) = 0 при x [δ, π] ,

2π

4. 21π R ω(x) dx = 1 ,

0

см. рис. 2.

Подобрать такую функцию нетрудно. Например, можно взять функцию k(cos πxδ + 1), ограничить ее сначала на интервал (−δ, δ), затем продолжить нулем на оставшуюся часть интервала [−π, π] и далее продолжить периодически на всю ось. Константу k следует выбрать так, чтобы выполнялось условие нормировки (4).

Ряды Фурье Интегралы Фурье Предметный указатель Литература

Веб – страница

Титульный лист

JJ II

J I

Страница 29 из 127

Назад

Полный экран

Закрыть

Выход

Мы покажем (со ссылкой на теорему 2.9), что свертка f ω годится на роль функции g. Заметим прежде всего, что в силу четности и периодичности,

2π

2π

2π

2π Z0

ω(t) dt = 2π Z0

ω(−t) dt = 2π Z0

ω(x − t) dt = 1 .

1

1

1

Тогда,

1

2π

1

2π

|f(x) − g(x)| = f(x)

Z

ω(x − t) dt −

Z f(t)ω(x − t) dt

2π

2π

0

0

1

2π

1

6

Z0

|f(x)

− f(t)|ω(x − t) dt =

Z

|f(x) − f(t)|ω(x − t) dt

2π

2π

|x−t|6δ

ε

Z

6

ω(x − t) dt = ε .

2π

|x−t|6δ

2.5. Сходимость рядов Фурье

Далее нам понадобится чуть более общий вариант леммы Римана-Лебега.

Теорема 2.14 (Лемма Римана-Лебега). Если f — непрерывная функция на [a, b],

то

b

Z

f(x)eiλx dx → 0 .

λ→∞

a

Ряды Фурье Интегралы Фурье

Предметный указатель

Литература

Веб – страница

Титульный лист

JJ II

J I

Страница 30 из 127

Назад

Полный экран

Закрыть

Выход