[ Буслов, Яковлев ] Введение в численный анализ

xmax

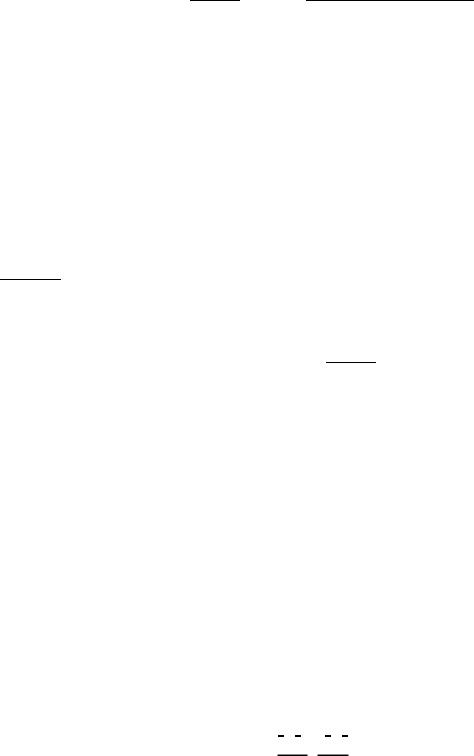
è

gn

=

jjAnjj

=

max

hPmaxg; gi + O([ 0= max]2n)

=

jj

jj

jjAn 1gjj

j

jrhPmaxg; gi + O([ 0= max]2n 2)

=

max

1 + O([ 0= max]2n 2)

g

:

j

jf

Т ким о р ом сли ст рто ый ктор g им л н нул ую про кцию н со ст нно по простр нст о от ч ющ м к- сим льному по мо улю со ст нному н ч нию (то сть Pmaxg =6 0 ), то при нн я ит р ционн я проц ур при о ит к н хо нию max . О н ко, хотя форм льно, пр ы ущ р ссмотр ни рно лишь случ н нул ой про кции,

йст ит льности и - оши ок окpу л ния при ычисл ниях эт пpо кция н pняк поя ится н н котором ш ильн йш прим н ни м то ит р ций при т к л мому р ульр ту. Попутно м тим, что сли по простр н- ст о от ч ющ max î íîì ðíî, òî ì òî èò ð öèé î íî ð ì ííî ïðè î èò ê í õî íèþ ñî ñò ííî î êòîð

îò ÷ þù î max . тим ктором с точностью о нормиро ки я ля тся

xmax = lim gn :

n!1

Ç ì ÷ íè . Äëÿ í õî íèÿ max мо но прим нять м то ит р ций и ол простой пост но к . Пусть l- я компон нт м ксим льно о со ст нно о ктор ст н ртном кли о ом ис н р н нулю (хотя ы о н т к я сущ ст у т), то

(Ang)l

max = nlim!1 (An 1g)l :

) Ì òî ñë î

И стно, что сл м трицы (сумм и он льных эл м нто ) р н сумм ¼ со ст нных н ч ний с уч том кр тности: P i = T rA , ò êèì î ð îì P mi = T rAm , è, ñë î ò ëüíî

T rAm = mmax[1 + ( 0= max)m + : : :] ;

0 сл ующ по мо улю м ксим льным со ст нно н ч ни . Т ким о р ом max ìî íî èñê òü ê ê ñë ó- þùèé ïð ë

j maxj = mlim

m

pT rAm ;

!1

èëè, í ïðèì ð, è

max =

lim

T rAm+1

:

T rA

m

m!1

Проц уру о ния м трицы ст п нь мо но оптими иpо ть:

A A A A ;

A2

A2

|

{z }

A4

| {z

}

и т к л , ч стности A16 = (A8)2 = A2222 .

|

{z

}

) Ì òî ñê ëÿpíûõ ïpîè íèé

тот м то я ля тся о о щ ни м м то ит р ций. Пусть

x è

y

прои ольны н ч льны кторы. Опр лим

èò ð öèè ym = Aym 1 = Amy =

mPsy ;

xm = Axm 1 =

mPsx . Àí ëî è÷íî ì òî ó èò ð öèé ó ìñÿ,

s

s

÷òî

P

P

71

= A 1y(n)) ,

hym; xmi ! max :

hym; xm 1i

6.2.3Î p òíû èò p öèè

Поиск миним льно о по мо улю со ст нно о н ч ния

Пусть y н который ст рто ый ктор. Опр лим о р тны ит р ции к к y(n) = Ay(n+1) èëè (y(n+1)

òî ñòü ýòî ïpÿì ÿ ÷ ëÿ í õî íèÿ ì êñèì ëüíî î ñî ñò ííî î í ÷ íèÿ max ì òpèöû B = A 1 о р тной к исхо ной м триц . Оч и но, что миним льно по мо улю со ст нно н ч ни м трицы A р но м ксим льному по мо улю со ст нному числу о р тной м трицы.

B	= A 1	1
	; ( i =		) :
i	i	i

Ì òî î p òíûõ èò p öèé ñî ñ è îì

Пусть A н ыро нн я эрмито м триц и н которо про но число. Р ссмотpим м трицу (A I) , со ст нными н ч ниями я ляются числ ( i ) , i со ст нны н ч ния исхо ной м трицы A . У о р тной м трицы (A I) 1 со ст нны н ч ния это личины i 1 . Ïpîö óp ì òî î ð òíûõ èò ð öèé cî ñ è îì

					y(n) = (A I)y(n+1) ;
	ïpè î èò ê í õî íèþ max		1		. Иными сло ми мы н хо им то со ст нно н ч ни j	, которо я ля тся
		j	i j
	i
	ли йшим к про ному числу		. В рьируя про но и но ь прим няя м то о р тных ит р ций со с и ом

мо но н йти с со ст нны н ч ния м трицы A .

6.3Н эрмито ы м трицы

6.3.1Дополнит льны с ния

В случ сли л р ич ск я и ом трич ск я кр тности со ст нных чис л оп р тор A со п ют, то унит рным пр о р о ни м (то сть пр о р о ни м сохр няющим ск лярно прои ни : hUx; Uyi = hx; yi ) ( RN | орто он льным пр о р о ни м) оп р тор при о ится к и он льному и у и н и он ли стоят со ст нны числ A с уч том кр тности. О н ко н р к ситу ция, ко л р ич ск я кр тность со ст нно о н ч ния пр ыш том трич скую (о р тно , кст ти, н о мо но).

 CN при опр л нном ы ор ис (н ы мым ор но ым или к нонич ским исом оп р тор A ) м триц оп р тор ст но ится лочно- и он льной. В к ом и локо ( ор но ых кл ток) м триц оп р тор я ля тся рхн тр у ольной и им т и

0		1	0	: : :			0	0	1
	0		1	: : :			0	0
	0	0		: : :			0	0	:	(1)
	. . . .				.		.	.
	. . .					. .
	. . .					. . .
@	0	0	0	: : :				1	A
B0		0	0	: : :			0	C
Р м ры ор но ых кл ток, их колич ст о, т к к к и числ									(корни х р кт ристич ско о ур н ния) я ляются

èí ðè íò ìè îï ð òîð A (òî ñòü í èñÿò îò û îð îð íî èñ ).

72

 RN ор но ис при о ит к кл тк м и (1) сли щ ст нный кор нь х р кт ристич ско о ур н ния м трицы оп р тор A к ком ли о ис . Поскольку коэффици нты х р кт ристич ско о полином м трицы оп р - тор RN щ ст нны, то м ст с к ым компл ксным корн м = +i он о т и компл ксно сопря нным= i . Жор но кл тк этом случ им т и

0

00

00

00

00

... ...

00

B 0 0 @ 0 0

1	0	0	0	: : :		0	0	1
0	1	0	0	: : :		0	0
		1	0	: : :		0	0
		0	1	: : :		0	0
0	0			: : :		0	0
0	0			: : :		0	0	:
. . . .						. .
. . . . ..						. .
. . . .					. . .
0	0	0	0	: : :		0	1
0	0	0	0	: : :				A
0	0	0	0	: : :			C

6.3.2М то ит p ций ля м ксим льно о по мо улю со ст нно о числ кp т- ности 2 случ оp но ой ном лии

От но имся по ро но н случ , ко м ксим льному по мо улю со ст нному н ч нию оп р тор A соот тст у т

ор но кл тк р м р 2 2 . В к нонич ском ис				u1; u2; : : : ; uN ì òðèö îï ð òîð				A èì ò è
		1	j	0	: : :	0
0 0						0 1
			j	0	: : :
							:
	0	0	j
	. .
B					B	C
	0	0
	. .
@	. .		j			A
			j
З сь B м триц , от ч ющ я ост шимся со ст нным н ч ниям, конкр тный и которой н с н инт р су т.
О о н чим у льный ис ч р v1; v2; : : : ; vN : Òî
Au1 = u1				A v1 = v1
Au2 = u2 + u1				A v2 = v2 + v1 :
 êòîð u1 я ля тся со ст нным ля оп р тор A соот тст ующим со ст нному н ч нию								.  êòîð u2 í û -
тся присо ин нным. Для сопря нно о оп р тор A			со ст нным и присо ин нным ктор ми, соот тст ующими

со ст нному н ч нию ( RN просто ) я ляются кторы у льно о ис v1 è v2 ñîîò òñò ííî. Ç ì òèì, ÷òî u1 = v2 , è u2 = v1 , то сть со ст нный ктор ля оп р тор я ля тся присо ин нным ля сопря нно о и н о орот.

Н при о ность о ычно о м то ит р ций

Бу м счит ть, что со ст нны н ч ния пронум тро ны поря к у ы ния мо уля и что 1 = . Пусть x прои ольный ктор. Р ло им о по ктор м ор но ис и у льно о к н му

	N	hx; viiui ; x =	N	hui; xivi
x =	P		P		:
	i=1		i=1

73

Ïî éñò ó ì í

x оп р тором A и сопря нным:

N

hx; viiAui ; A x

N

hui; xiA vi ;

Ax =

P

=

P

i=1

i=1

èëè

N

Ax = ( < x; v1 > + < x; v2 >)u1 + < x; v2 > u2

+

X

< x; vi > Aui ;

i=3

N

A x = ( < u1 ; x > + < u2; x >)v1 + < u2; x > v2

+

X

< ui; x > A vi :

i=3

Ан ло ично, поскольку

n n n 1

j

0 : : : 0

0 0

n

0 1

j

0 : : :

An =

;

0

0

j

.

.

n

B

C

0

0

.

.

B

@

.

.

j

A

òî

j

Anx = ( n < x; v1 > +n n 1 < x; v2 >)u1 + n < x; v2 > u2 + : : : :

(2)

К р тичн я форм n-ой ст п ни оп р тор A с исполь о ни м (2) мо т ыть пис н к к

N

X

hAnx; xi = hAnx;

1

hui; xivii

=

1

1

2

2

n

1

1

o

n

2

1

= n

a + b n

+ O

[ 0

= ]n

;

a =< x; v >< u ; x > + < x; v

>< u ; x > (= 2 < x; v

>< u ; x > R ),

b =< x; v

>< u ; x > è 0

ñë óþù ïî ìî óëþ

ñî ñò ííî í ÷ íè .

В н ш й ситу ции щ ст нно. По н ло ии с м то ом ск лярных прои ний, прим ня мым ля эрмито ых м триц, р ссмотpим отнош ни Р л я

h

i

h

i

a +

(2n+1)b

2n

0

An+1x; A nx

A2n+1x; x

n = h Anx; A nx i = h A2nx; x i =

2nb

+ O

=

a +

1 +

a +

b

2n

n

1

o

=

+ O

0=

=

1 + O

:

a + 2nb

n

Èò ê, n = f1 + O(1=n)g , то сть схо имость при

n

! 1

н стольно н у о л т орит льн я, что т ря т пр кти-

ч ский смысл. Т ким о р ом о ычными ит р ционными м то ми со ст нно число случ оp но ой ном лии у о л т орит льно сосчит ть н пр ст ля тся о мо ным. Н о хо им к кой-то ру ой по хо .

Мо ифициро нный м то ит р ций

Сост им к р тно ур н ни , ля которо о я ля тся корн м кp тности 2

	(t )2 = t2 + pt + q = 0 p = 2 ; q = 2 :
Коэффици нты p и q	р н н и стны, поскольку н и стно с мо . Попыт мся их опр лить. О о н чим
xn = Anx и р ссмотрим	ûð íè

74

xn+1 + pxn + qxn 1 =< x; v1 > f

1n+1 + p

1n

+ q 1n 1

g u1+

|

{z

}

=0

2

n

n

1

n 2

1

2

n+1

n

n 1

2

+ < x; v

> f(n + 1) 1

+ pn 1

+ q(n

1) 1

gu

+ < x; v

> f 1

+ p 1

+ q 1

g u

+ : : : =

=< x; v > fn ( + p + q) + q gu + : : : =< x;|v > {z(

q) u

}+ : : : ;

=0

2

n 2

2

n

n 2

1

1

n 2

2

1

4

| {z

}

|

{z

}

=0

=0

поскольку

2

q) =

p2

q = 0 . Ò êèì î p îì x

n+1

+ px

n

+ qx

n

1

= o(x

n+1

) . Ïðè ýòîì êîîð èí òû n-îé èò ð öèè

(

xk óò ñ ÿ ê ê ñîîò òñò óþù ÿ ñò ï íü :

xin

= (Anx)i

nxi

, поэтому ст ст нно сти три ктор

yn+1;n;n 1

=

x

n+1;n;n 1

. Для коор ин т этих кторо , к к сл у т и пр ы ущ о ыполн но

n+1

ykn+1 + pykn + qykn 1 = O([ 0= ]n+1) :

Выпиш м соот тст ующи р нст ля п ры коор ин т, ск м k и l.

yn

yn+1 + pyn + qyn 1 = O [ 0= ]n+1

0

yn 1

l

k

k

k

[ 0= ]n+1

l

:

ykn

yln+1 + pyln + qyln 1 = O

0

ykn 1

Домно я п р о р нст о н

n

1

, òîðî í

n

1

yl

yk

и ычит я и п р о о р нст торо , получ м

p =

ykn+1yln 1

yln+1ykn 1 + O

0=

n+1

=

yknyln 1

ylnykn 1

= xkn+1xln 1 xln+1xkn 1 + O

0

=

n+1

:

n

n

xnxn 1xnxn 1

k

l

l

k

Àí ëî è÷íî, îìíî ÿ ï ð î ð íñò î í yl

, òîðî í

yk

и ычит я их п р о о р нст торо , получ м

q =

xkn+1xln

xln+1xkn

+ O

0=

n+1

:

xkn 1xln

xln 1xkn

З м тим, что н о хо имо колич ст о ит р ций пр ло нном м то , мо но контролиро ть исхо я и то о, что

ол но ыполнятся р нст о

p2=4 = q .

75

76

Ãë 7

Поиск минимум

7.1Ñëó÷ é î íîé ï ð ì ííîé

7.1.1	М то олото о с ч ния
Пусть	(x) : [a; b] ! R и и стно, что н пром утк [a; b] функция	им т хотя ы о ин лок льный минимум.
Для прим н ния и л мо о ни м то олото о с ч ния, от функции		(x) н тр у тся н пр ры ность,

ост точно лишь кусочной н пр ры ности. Бу м пок счит ть, что им т н пром утк лишь о ин лок льный минимум (он и ло льный).

М то осно н н ср н нии н ч ний функции р личных точк х, с посл ующим от р сы ни м пром утко , н которых минимум у точно н мо т н хо иться. сно, что что ы осущ ст лять по о ную проц уру, н о хо имон ть н ч ния функции, оо щ о оря, 4-х точк х. Д йст ит льно, пусть a = x0 < x1 < x2 < x3 = b , и пусть, ск м, точк x2 н ч ни функции н им ньш и этих ч тыр х личин. То минимум омо н мо т н хо иться н пром утк [x0; x1] и поэтому этот пром уток мо но от росить. Т п рь н ост ш мся пром утк [x1; x3] н м и стны кр йни н ч ния функции и н ч ни о ной нутр нн й точк . До ляя но ую точку x4 мы мо м по торить ср н ни н ч ний и но ь су ить опустимый пром уток. К к н и ол р умно р м - щ ть о ля мы точки? Пр ст ля тся ст ст нным, что ы л ни отр ко происхо ило по о но пр ы ущ мул нию.

x0 x1 x2 x4 x3

то о н ч т, ч стности, что нутр нни точки ол ны р спол ться симм трично, то сть jx1 x0j = jx3 x2j = h . Если лин исхо но о пром ут р н l , то ол но ыполняться соотнош ни

= h	= x1 x0	= x2 x1 = l 2h									;
l	x3 x0		x3 x1							l h
îòêó
= h = 1 2				h		= 1 2
				l						:
	l 1		h				1
			l
Р р ш я к р тно ур н ни относит льно , получ м =							3 2p		0; 38 , то сть н к ом ш ( исключ ни м
								5
ычисл ния ст рто ых нутр нних точ к x1 è	x2 ) îòð îê ñîêð ù òñÿ										1=(1 ) 1; 61 р и схо имость м то
ëèí éí ÿ.

77

@

@xi

Т ким о р ом, ля то о, что ы н ч ть проц сс олото о с ч ния, к р ничным точк м x0 = a è x3 = b о ляются

точки x1 = x0+ (x3 x0) x2 = x3 (x3 x0). З т м посл от p сы ния точ к и о л ния но ых, н посл ующих ш х ном р точ к п p м ш ны споpя очно. Д им им ном p j,k,l,m , и пусть (xj ) < (xk;l;m) . При л нии по олотому с ч нию от р сы тся отр ок о ним, и концо которо о я ля тся точк н и ол у л нн я от xj . Пусть этой точкой я ля тся xk (оч и но, что это о н и кр йних точ к). З т м н о о ить но ую точку xn . Пусть ля опp л нности xk < xj < xm . То силу симм трии р споло ния нутр нних точ к он опр ля тся соотнош ни м xn = xk + xj xi (т. . сумм кp йних точ к минус нутр нняя).

Если функция им т н исхо ном пром утк н сколько лок льных минимумо , то м то олото о с ч ния с¼ р но сой тся к о ному и них, н о я т льно к ло льному.

7.1.2Ì òî ï p îë

Если функция о л т ост точной л костью (им т тоpую пpои о ную) то ст ст нно исполь о ть это о стоят льст о при поиск минимум . В этой точк 0(x) = 0, и мо но иск ть нуль п p ой пpои о ной, ск м м то ом Ньютон

0(xn) xn+1 = xn 00(xn) :

ту фоpмулу л ко получить и н посp ст нно p ло и (x) pя Т йлоp точк xn и о p ничи шись тp мя чл н ми, т. . ппpоксимиpуя кpи ую п p олой

(x) (xn) + (x xn) 0(xn) + (x 2xn)2 00(xn) :

Минимум этой п p олы н хо ится к к p точк xn+1. В с я и с этим м то и н ы тся м то ом п р ол. Вычислять и п p ую и тоpую пpои о ную н к ом ш о ольно н кл но. Поэтому их пpи ли нно м няют

p ностными прои о ными, ычисл нными с помощью спомо т льно о ш h :

0(xn)				!	(xn + h) (xn h) ;
					2h
00(xn)	!		(xn + h) 2 (xn) + (xn h)			;
					h2
и м то приним т и
xn+1 = xn			h		(xn + h) (xn h)		:
		2 (xn + h) 2 (xn) + (xn h)

Кст ти, этот по хо эк и л нт н м н кpи ой н инт pполяционную п p олу, постpо нную по тp м точк м xn h; xn; xn + h с посл ующим н хо ни м минимум этой п р олы (точки xn+1).

З м ч ни . Ум стно ср нить м то ы поиск минимум и м то ы поиск корня ур н ния. Т к м то олото о с - ч ния по о н ихотомии. И том и ру ом н функцию н кл ы ются миним льны о р нич ния. Они чр ыч йно просты и н ны, поря ок схо имости о оих м то х лин йный. М то п р ол этом смысл по о н м то у Ньютон . От функции тр у тся ольш , схо имость ыстр . Поиск минимум по м то у п р ол соот тст у т поиску корня по м то у с кущих.

7.2Функции мно их п р м нных

Пусть : M ! R ; M RN и пусть 2 CM2 . В точк х минимум = 0 ; i = 1 ; : : : ; N, к к пpоч м и точк х м ксимум и с ло ых точк х. Но р ло ни pя Т йлоp окp стности н ыро нной точки минимум x

78

(x) = (x ) +					1		N	@2 2 xi xj + : : :
					2	X		@x
						i;j=1		i
	N	@2
û ë íî ò ì, ÷òî ê ð òè÷í ÿ ôîðì				xi xj				поло ит льно опр л н (н помним, что к р тичн я
		2
	i;j=1	@x	i
ôîðì í û òñÿ ïîëî èò ëüíî îïð ë ííîé,P ñëè					P		aijzizj jjzjj2; > 0, z = (z1; z2 : : : ; zN )T ).

7.2.1Коор ин тный спуск

Проц уру коор ин тно о спуск р ссмотрим н прим р функции ух п р м нных (x:y). Пусть (x0; y0) н котор я точк . З фиксиру м п р м нную y и н й м минимум функции (x; y0) к ким ли о и у и стных спосо о поиск минимум функции о но о п р м нно о (спуск по п р ой коор ин т ). Пусть этот минимум ости тся точк x1. З фиксиро это н ч ни н й м минимум функции (x1; y) (спуск по торой коор ин т ). Пусть он н хо итсяточк y1. Т п рь н й м минимум функции (x; y1) (сл ующий спуск по п р ой коор ин т ) и т. . Т кой м то поиск минимум н ы тся коор ин тным спуском. В исимости от с ойст функции и поло ния н ч льной точки, проц сс мо т сойтись к экстр м льной точк или н т. Отм тим ост точый при н к схо имости коор ин тно о спуск . Если ы н пр ры но ифф р нциру м о л сти M, со р щ й точку минимум x и к р тичн я

N

@2

поло ит льно опр л н , то н которой окр стности x м то коор ин тно о спуск схо ится

ôîðì

P

xi xj

2

i;j=1

@x

i

к ук нному минимуму. Док т льст о про м ля случ я ух п р м нных. Пусть xx

a ; yy

b ;

j

xy

j

c,

a; b; c > 0 è ab > c2 о л сти M (это о н ч т ч стности, что м триц торых прои о ных поло ит льно опр л н ). Бу м счит ть, что точк A = (x0; y0) получ н р ульт т спуск по п р м нной y , т. . y(A) = 0 . Пусть j x(A)j = 1 .  òî÷ê B = (x1; y0) î ð ù òñÿ íóëü x , ìî óëü y р н н которому числу . Т ким о р ом

1 = j x(A) x(B)j = j xx( )j (A; B) a (A; B) ;

= j y(A) y(B)j = j xy( 0)j (A; B) c (A; B) ;

îòêó

c 1 a :

(1)

 òî÷ê C = (x1; y1) : y = 0; è x = 2, ïðè ýòîì

2 = j x(C) x(B)j = j xy( )j (C; B) c (C; B) ;
= j y(C) y(B)j = j yy( 0)j (C; B) b (C; B) ;
è, ñë î ò ëüíî,
	c b 2 :		(2)
È (1) è (2) êëþ÷ ì, ÷òî 2 q 1, 0 q	c2	< 1. Т ким о р ом с к ым циклом x	óì íüø òñÿ ê ê
	ab

минимум q р . Ан ло ично у ы т и ч стн я прои о н я по п р м нной y. Т ким о р ом коор ин тный спускйст ит льно схо ится к точк минимум .

79

7.2.2Н искор йший спуск

Спуск мо но осущ ст лять н только оль коор ин тных ос й, оо щ оль лю о о н пр л ния. Пусть a прои -ольный иничный ктор, ющий н пр л ни . Функция '0(t) = (r0 + at) сть функция о ной п р м нной иминимум я ля тся минимумом функции (r) н прямой r0 + at . Åñëè û ð òü a = a0 = grad jr0 , то a у т я ляться н пр л ни м н и ольш о у ы ния функции точк r0 . Осущ ст им спуск оль это о н пр л ния (то сть н й м минимум функции '(t) ). Пусть он н хо ится точк r1. Ò ï ðü ýòîé òî÷ê û ð ì íî î í ïð - ë íè a1 = grad jr1 и осущ ст им спуск оль н о и т. . З м тим, кст ти, что кторы a0 è a1 орто он льны. Опис нный м то спуск н ы тся н искор йшим.

Хотя при н искор йш м спуск и ни происхо ит оль н пр л ния н ольш о у ы ния функции т кущ й точк rk , о н ко поря ок схо имости ост тся т ким , к к и при покоор ин тном спуск (при этом прихо ится к ой точк rn но о счит ть р и нт). Д ло сь том, что при с и от точки rn н пр л ни н и ыстр йш о у ы ния функции и м ня тся. О ычно спуск прои о ят н точно о минимум , н сколько м ньш . То сть, сли 'n(t) = (rn + ant) , и минимум функции 'n(t) îñòè òñÿ òî÷ê tn , то спуск осущ ст ля тся о точки tn ,

< 1 . В "и л "мо но спуск ться н скон чно м лую личину и но о корр ктиро ть н пр л ни . При этом кри я спуск r(t) у т у о л т орять ур н нию

dr(t) = grad (r(t)) : dt

О н ко инт риро ни т кой сист мы ур н ний ч стных прои о ных пр ст ля т со ой от льную н простую

÷ó.

7.2.3М то сопря нных н пр л ний

В окр стности точки минимум функция (r) т с я о ычно к к к р тичн я функция. Бу м счит ть ля н ч л , что он я ля тся точности к р тичной, т. .

(r) = hr; Ari + hr; bi + c :

Ç ñü b 2 RN (Cn), c 2 R, A поло ит льно опр л нн я м триц . Поскольку A поло ит льно опр л н , то к р тичн я форм

hx; yiA = hx; Ayi

у о л т оря т с м с ойст м ск лярно о прои ния. В м ортонормиро нный ис feigNi=1 ëèí éíîì ïðî-

стр нст с нормой h ; iA. Бу м н ы ть н пр л ния, мы им, сопря нными. Если r0 н котор я точк , то

N

ïðîè îëüí ÿ òî÷ê r ïð ñò ëÿ òñÿ è r = r0 + P iei. Òî

1

(r) = r0 + X iei; Ar0 + X iAei + r0 + X iei; b + c =

N

= (r0) + X 2i + 2 ihei; r0i + ihei; bi :

i=1

В этой сумм отсутст уют п р кр стны чл ны, т ким о р ом спуск оль лю о о н пр л ния ei миними иру т лишь с ой чл н суммы. то о н ч т, что осущ ст и спуск по к ому и сопря нных н пр л ний лишь о ин р мы точности ости м минимум . В точк минимум

@	i		0
	= 2 i + 2he	; Ar		+ b=2i = 0 ; i = 1; 2; : : : N ;
@ i

îòêó i = hei; Ar0 + b2 i.

80