
Лекция 5
Общее решение задачи Джонсона методом ветвей и границ.
Пусть
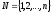 - множество работ, которые выполняются
наm
ма-шинах, причем все работы проходят
имеющиеся машины в одной и той же
последовательности. Требуется найти
такой порядок запуска работ на испол-нение,
при котором суммарное время простоя
всех машин будет минималь-ным.
- множество работ, которые выполняются
наm
ма-шинах, причем все работы проходят
имеющиеся машины в одной и той же
последовательности. Требуется найти
такой порядок запуска работ на испол-нение,
при котором суммарное время простоя
всех машин будет минималь-ным.
Очевидно,
что имеется всего
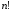 таких порядков запуска на исполнение,
каждый из которых представляет собой
перестановку
таких порядков запуска на исполнение,
каждый из которых представляет собой
перестановку номеров работ
номеров работ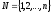 .
.
Организацию полного перебора вариантов можно, в частности, провести методом ветвей и границ. Перед тем, как описать применение этого метода к поставленной задаче, заметим, что искомая последовательность ра-бот, минимизирующая суммарное время простоя машин, является минимизи-рующей и общее время выполнения всех работ. Ниже мы будем искать эту последовательность работ, как обладающую именно этой последней характе-ристикой: минимальное время выполнения всех работ.
Для
большей ясности мы будем далее
предполагать, что
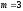 .
.
Итак,
пусть
- множество всех
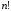 последовательностей
последовательностей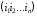 .
Пусть
.
Пусть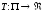 - функция, сопоставляющая каждому
расписанию
- функция, сопоставляющая каждому
расписанию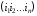 время завершения всех работ. Требуется
найти минимум этой функции.
время завершения всех работ. Требуется
найти минимум этой функции.
Согласно методу ветвей и границ, нужно построить оценочную функ-цию на множестве подмножеств множества и систему разбиений этого множества, приводящую к рекорду.
Построим
три вспомогательные функции на множестве
подмножеств множества ,
которые обозначим, соответственно,
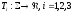 .
Пусть символ
.
Пусть символ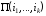 обозначает множество всех расписаний,
начинающихся с последовательности
обозначает множество всех расписаний,
начинающихся с последовательности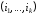 .
Очевидно, символ
.
Очевидно, символ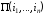 обозначает мно-жество, состоящее из
единственного элемента
обозначает мно-жество, состоящее из
единственного элемента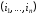 .
.
Итак, пусть
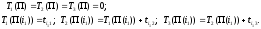
Таким
образом,
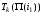 - время окончания исполнения работы
- время окончания исполнения работы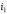 наk-ой
машине. Далее определим функции
наk-ой
машине. Далее определим функции
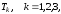 рекуррентно:
рекуррентно:
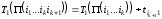 ,
,
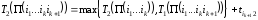 ,
,
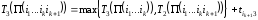 .
.
Теперь
можно построить сразу три оценочных
функции для множеств
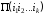 ,
которые будем обозначать так:1,
2
и 3.
Вот их определение (мы будем обозначать
для удобства записи
,
которые будем обозначать так:1,
2
и 3.
Вот их определение (мы будем обозначать
для удобства записи
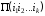 черезx
и через
черезx
и через
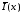 те работы из множества
те работы из множества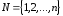 ,
которых нет среди работ
,
которых нет среди работ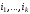 ):
):
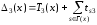 ;
;
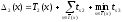 ;
;
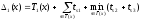 .
.
Тот факт, что эти функции - оценочные, можно доказать; аналогично, можно доказать то же самое в отношении функции
 ;
;
она - оценочная.
Лекция 6
Системы массового обслуживания (СМО): определение, классификация, построение графа состояний. Введение основных характеристик.
Предположим, что имеется набор последовательно возникающих заявок, выполнение каждой из которых есть некое действие, осуществляемое специальным устройством - узлом обслуживания. Например, узел обслуживания - это железнодорожная касса, в которую в качестве «заявок на обслуживание» заходят пассажиры за билетами.
Схематически эту ситуацию можно изобразить так:
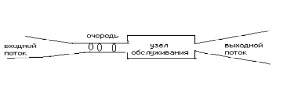
Это - ситуация системы массового обслуживания (СМО).
Особенность обсуждаемой ситуации: заявки приходят на обслуживание хаотично, в случайные моменты времени. И вторая особенность: время, в течение которого заявка находится в СМО (в очереди и в узле обслуживания) - тоже величина случайная. Приняты две классификации СМО - по типу очередиипотипу узла обслуживания.
Будем говорить, что некая СМО находится в состоянии Еkв момент времениt0, если в этот момент в ней находится ровноkзаявок. С каждой СМО принято связывать специальный граф -граф состояний, - который строится следующим образом: его множеством вершин является множество всех возможных состоянийЕk(k=0,1,2,...), а ребро (Ei, Ej) включается тогда и только тогда, когда СМО в процессе своей работы может перейти из состоянияEiв состояниеEjнепосредственно, т.е. минуя все остальные состояния.
Как было сказано выше,
важнейшая особенность СМО как объекта
изучения состоит в том, что заявки
приходят в СМО на обслуживание в случайные
моменты времени. Следовательно, переход
СМО из одного состояния в другое есть
событие случайное. Пусть
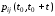 -
вероятность того, что СМО переходит из
состоянияEiв состояниеEjза период времени
-
вероятность того, что СМО переходит из
состоянияEiв состояниеEjза период времени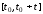 ,
причем здесь и всюду в дальнейшем, если
только не будет оговорено иное,
предполагается именно такая пара
состояний (Ei,
Ej),
которая составляет ребро в графе
состояний. Введенные вероятности
называютсяпереходными вероятностямиСМО.
,
причем здесь и всюду в дальнейшем, если
только не будет оговорено иное,
предполагается именно такая пара
состояний (Ei,
Ej),
которая составляет ребро в графе
состояний. Введенные вероятности
называютсяпереходными вероятностямиСМО.
Если
все переходные вероятности
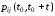 не
зависят от аргумента
не
зависят от аргумента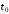 ,
т.е. для всех ребер графа состояний
,
т.е. для всех ребер графа состояний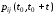 =
=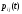 ,
то СМО называетсястационарной.
Всюду в дальнейшем именно такие и только
такие СМО будут рассматриваться. Именно
для стационарных СМО слова «граф
состояний» обозначают не только тот
граф состояний, который был введен выше,
но еще и совокупность функций
,
то СМО называетсястационарной.
Всюду в дальнейшем именно такие и только
такие СМО будут рассматриваться. Именно
для стационарных СМО слова «граф
состояний» обозначают не только тот
граф состояний, который был введен выше,
но еще и совокупность функций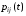 ;
таким образом, граф состояний (стационарной)
СМО - это взвешенный граф, в котором роль
графа играет прежний граф состояний, а
весовой функцией является функция,
сопоставляющая каждому ребру функцию
;
таким образом, граф состояний (стационарной)
СМО - это взвешенный граф, в котором роль
графа играет прежний граф состояний, а
весовой функцией является функция,
сопоставляющая каждому ребру функцию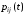 .
.
Функции
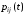 называютсяфункциями переходных вероятностейили простопереходными вероятностями;
бывает удобным в рассмотрениях следующий
объект:матрица переходных вероятностей:
называютсяфункциями переходных вероятностейили простопереходными вероятностями;
бывает удобным в рассмотрениях следующий
объект:матрица переходных вероятностей:
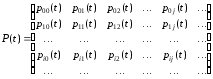 .
.
Заметим, что сумма элементов любого столбца этой матрицы (как и сумма элементов любой строки) равна единице – ведь эти элементы – вероятности событий, составляющих полную группу.
СМО
называется системой без последействия,
если функции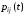 не
зависят от того, как именно СМО попала
в состояниеEi.
Именно такие СМО рассматриваются в
дальнейшем. Таким образом, мы будем
обсуждать только стационарные СМО без
последействия.
не
зависят от того, как именно СМО попала
в состояниеEi.
Именно такие СМО рассматриваются в
дальнейшем. Таким образом, мы будем
обсуждать только стационарные СМО без
последействия.
