
Лекция 7
Основные характеристики СМО. Пуассоновский поток заявок, экспоненциальное время обслуживания.
Рассмотрим
теперь величину
 при
при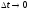 .
Если эта величина стремится к нулю при
.
Если эта величина стремится к нулю при для всехi,jтаких, что
для всехi,jтаких, что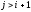 или
или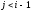 ,
то СМО называетсяординарной. По
смыслу это означает, что в ординарную
СМО за короткий промежуток времени не
может поступить более одной заявки и
из ординарной СМО за короткий промежуток
времени не может выйти более одной
заявки.
,
то СМО называетсяординарной. По
смыслу это означает, что в ординарную
СМО за короткий промежуток времени не
может поступить более одной заявки и
из ординарной СМО за короткий промежуток
времени не может выйти более одной
заявки.
Мы будем в дальнейшем рассматривать только стационарные ординарные СМО без последействия.
Заметим
следующее обстоятельство. Пусть
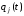 -
вероятность того, что СМО попадает в
течение времениtв
состояниеEjи
-
вероятность того, что СМО попадает в
течение времениtв
состояниеEjи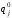 - вероятность того, что в некоторый
начальный момент времени СМО была в
состоянииEj.
Если обозначить
- вероятность того, что в некоторый
начальный момент времени СМО была в
состоянииEj.
Если обозначить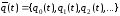 и
и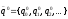 ,
то, согласно формуле полной вероятности
и правилу умножения матриц, окажется
выполненным равенство:
,
то, согласно формуле полной вероятности
и правилу умножения матриц, окажется
выполненным равенство:
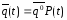 .
.
Промежуток времени между последовательно поступающими заявками в СМО есть величина случайная. Если функция распределения этой случайной величины имеет вид
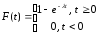
при
некотором
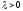 ,
то поток заявок называетсяпуассоновским.
,
то поток заявок называетсяпуассоновским.
Время, в течение которого очередная заявка в СМО находится на обслуживании, также является величиной случайной. Если функция распределения этой случайной величины имеет вид
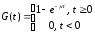
при
некотором
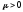 ,
то время обслуживания называетсяэкспоненциальным.
,
то время обслуживания называетсяэкспоненциальным.
Прежде, чем анализировать особенности СМО с пуассоновским потоком заявок и экспоненциальным временем обслуживания, приведем некоторые стандартные конструкции.
Положим
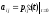 и
введем матрицу
и
введем матрицу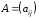 .
Число
.
Число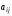 называетсяинтенсивностьюперехода
СМО из состояния
называетсяинтенсивностьюперехода
СМО из состояния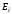 в состояние
в состояние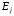 .
Когда
.
Когда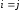 ,
число (
,
число (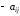 )
называютинтенсивностью выхода СМО
из состояния
)
называютинтенсивностью выхода СМО
из состояния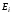 .
Полезно заметить, учитывая, что при
.
Полезно заметить, учитывая, что при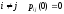 ,
а при
,
а при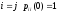 ,
справедливы неравенства:
,
справедливы неравенства:
при
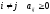 ,а при
,а при
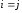
 .
.
Матрица
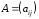 называетсяматрицей интенсивностейСМО.
называетсяматрицей интенсивностейСМО.
Можно
доказать, что вероятности
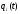 ,
введенные в этой лекции,удовлетворяют
системе линейных дифференциальных
уравнений
,
введенные в этой лекции,удовлетворяют
системе линейных дифференциальных
уравнений
(7.1)
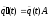
при
начальных условиях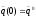 (здесь
(здесь ).
).
Из ординарности СМО следует, что в ее матрице интенсивностей отличными от нуля могут быть элементы только на главной диагонали и на двух ближайших к ней и параллельных ей линиях:
 .
.
Это обстоятельство делает систему уравнений (7.1) более конкретной. В частном случае, например, при пуассоновском потоке входных заявок (можно проверить, что в этом случае СМО будет стационарной, ординарной и без последействия) и полном отсутствии обслуживания (это значит, что заявки только поступают в СМО, но не покидают СМО) матрица Aпринимает вид
 ,
,
после чего система (7.1) решается рекуррентно стандартными средствами. В результате получается ответ:
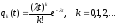 .
.
Это означает, что в СМО с пуассоновским потоком заявок и любым режимом обслуживания вероятность поступления k заявок
за
время t равна
 .
.
Лекция 8
Особенности пуассоновского потока заявок и экспоненциального времени об-служивания. СМО типа (m,n).
Из
сказанного в предыдущей лекции следует,
что в случае пуассоновского потока
заявок имеется полное описание ряда
случайной величины, которую представляет
собой число заявок, поступивших за время
t. Это позволяет подсчитать ее математическое
ожидание
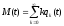 .
Соответствующий ответ выглядит так:
.
Соответствующий ответ выглядит так: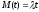 .
Это значит, что
.
Это значит, что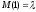 .
Следовательно, смысл пуассоновского
параметра в том, что это - среднее число
заявок, поступающих в единицу времени.
.
Следовательно, смысл пуассоновского
параметра в том, что это - среднее число
заявок, поступающих в единицу времени.
Можно провести аналогичные рассуждения в связи с экспоненциальным временем обслуживания. А именно, если
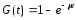 -
-
функция распределения времени обслуживания (при неотрицательных значениях t, а при отрицательных - она равна нулю), то математическое ожидание времени обслуживания есть число
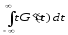 .
.
Стандартное
интегрирование по частям дает ответ -
число
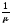 .
Следовательно, среднее время обслуживания
одной заявки равно
.
Следовательно, среднее время обслуживания
одной заявки равно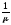 (при экспоненциальном обслуживании);
поэтому в единицу времени (при
экспоненциальном обслуживании) в среднем
обслуживается
(при экспоненциальном обслуживании);
поэтому в единицу времени (при
экспоненциальном обслуживании) в среднем
обслуживается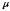 заявок.
заявок.
Рассмотрим теперь следующую модель СМО. Предположим, что ее узел обслуживания имеет n одинаковых устройств и очередная приходящая заявка попадает на любое из этих устройств для обслуживания. Если оказывается, что все устройства заняты, то заявка становится в очередь и ожидает, когда какое-либо устройство освободится. Предположим, что число мест в очереди равно m. Наконец, будем предполагать, что входной по-
ток заявок - пуассоновский с параметром
 ,
а время обслуживания - экспоненциальное
с параметром
,
а время обслуживания - экспоненциальное
с параметром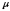 .
Такие СМО называются СМО типа (m, n).
.
Такие СМО называются СМО типа (m, n).
Граф состояний такой СМО выглядит очень просто:
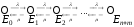 ,
,
причем около ребер-стрелок в данном случае указаны лишь интенсивности перехода из состояния в состояние.
