Контрольная работа №2

8. Классическим методом и методом операционного исчисления найти частное решение системы дифференциальных уравнений 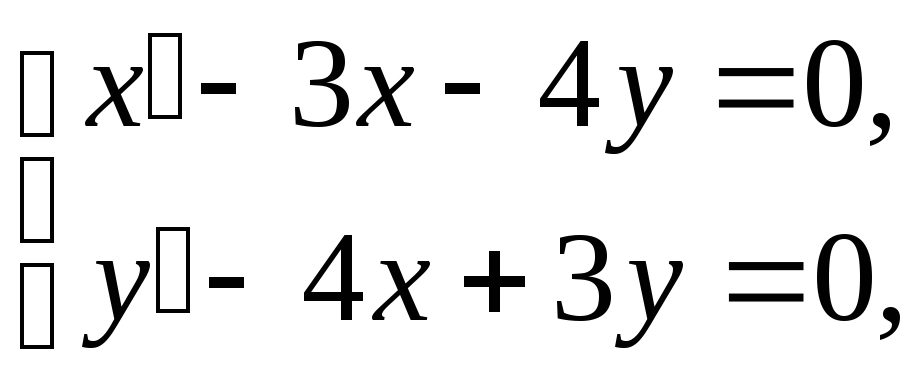удовлетворяющее начальным условиям .

Решение. Решением этой системы является пара функций ,, удовлетворяющих системе, причем .

1) Классический метод решения.

Продифференцируем первое уравнение по переменной :

.

Из первого уравнения определяем , следовательно, из второго уравнения имеем

.

Подставляем в уравнение, полученное после дифференцирования, приходим к уравнению

,

– линейное дифференциальное уравнениеII порядка с

постоянными коэффициентами.

Составляем характеристическое уравнение и находим его корни:

– действительные различные корни.

В этом случае общее решение дифференциального уравнения имеет вид

,

.

Ранее определили . Тогда

.

Общее решение системы

Находим значения произвольных постоянных, используя начальные условия :

Частное решение системы

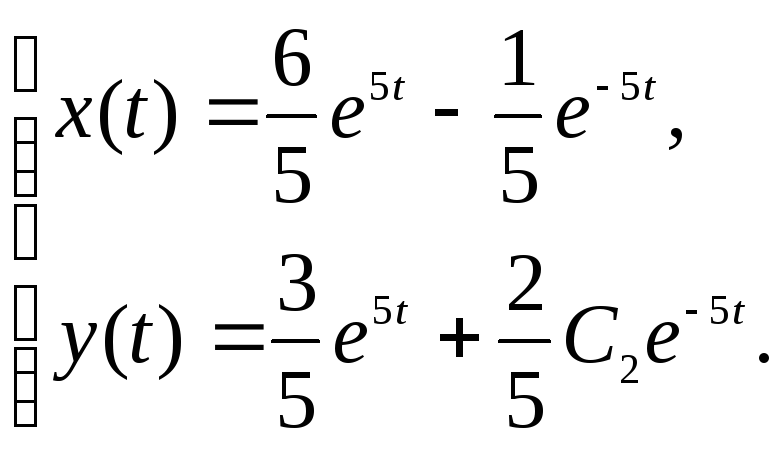
2) Метод операционного исчисления.

Пусть . По теореме о дифференцировании оригинала получим

Следовательно, операторная (изображающая) система имеет вид:

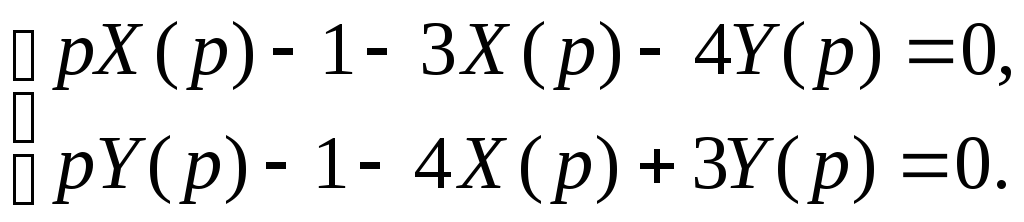
Из первого уравнения определяем

и подставляем во второе уравнение:

,

.

Представим дробь в виде суммы простых дробей:

Следовательно, .

По таблице изображений находим

.

Аналогично:

,

,

.

Частное решение системы

9. Найти область сходимости степенного ряда .

Решение. Общий член ряда . Для исследования ряда на сходимость применим признак Даламбера:

.

Таким образом, при , то есть приисходный ряд сходится абсолютно.

Выясним вопрос о сходимости ряда на концах интервала сходимости. При заданный ряд принимает вид

.

Это числовой знакочередующийся ряд. Его общий член по абсолютной величине монотонно убывает и стремится к нулю при . Таким образом, оба условия признака Лейбница выполнены и ряд сходится, то есть точкапринадлежит области сходимости заданного степенного ряда.

При исходный ряд принимает вид

.

Это числовой знакоположительный ряд, который расходится (сравните его с гармоническим рядом . Следовательно, точкане принадлежит области сходимости заданного степенного ряда.

Таким образом, область сходимости исходного степенного ряда . Вне этого интервала ряд расходится.

10. Разложить заданную функцию в ряд Фурье по синусам на отрезкеи построить результирующую первых двух гармоник полученного ряда.

Решение. Так как по условию ряд должен содержать только синусы кратных углов, то следует продолжить заданную функцию на отрезок нечетным образом, затем продолжить на всю числовую ось с периодом. Теперь разложим полученную периодическую функцию в ряд Фурье (эта операция разложения называется гармоническим анализом) вида:

.

Так как заданная функция нечетная, то коэффициенты ряда Фурье , авычисляем по формуле

и ряд Фурье имеет вид .

Подставляя заданную функцию, получаем

.

Последний интеграл вычисляем методом интегрирования по частям, полагая . Отсюда. следовательно,

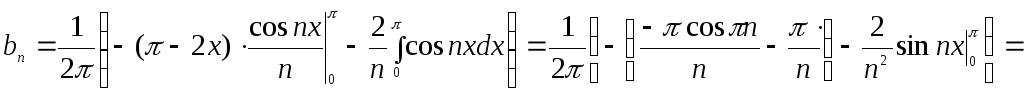
Таким образом, искомое разложение имеет вид

или

В полученном разложении возьмем первые две гармоники: , ; построим их графики; путем сложения ипостроим график результирующейи данной функциина отрезке.

у

0,78 

0,5 =

1/4

0 х

–1/4

–0,5 = –

–0,78 –

(– – – – – )( )+(––––––)

11. Дана функция двух переменных . Найти:

1) экстремум функции ;

2) в точкеА(1; –2);

3) наибольшую скорость возрастания точкеА(1; –2).

Решение. 1) Для отыскания экстремума функции предварительно найдем частные производные первого и второго порядка:

Приравняем их к нулю и решим систему уравнений:

Решением системы является точка М(–4; 1). Точка М(–4; 1) называется подозрительной на экстремум. Найдем частные производные второго порядка в точке М:

Из них составим определитель второго порядка

Так как , то в точкеМ(–4; 1) есть экстремум. Производная , а, значит, это точка минимума функции.

2) Градиент функции найдем по формуле:

,и были найдены в пункте 1.

.

Градиент функции в точкеА(1; –2):

.

3) Наибольшая скорость возрастания функции равна модулю градиента:

.

12. а) Найти объем тела, ограниченного параболоидом , цилиндром и плоскостью, через тройной интеграл, применяя цилиндрическую систему координат.

б) Найти объем тела, ограниченного сферой и конусом , через тройной интеграл, применяя сферическую систему координат.

в) Найти поток векторного поля через полную поверхность пирамиды , образованной данной плоскостью: и координатными плоскостями ,,в направлении внешней нормали к ее поверхности, применив теорему Остроградского–Гаусса.

г) С помощью двойного интеграла вычислить координаты центра тяжести фигуры (меньшей по площади), ограниченной эллипсом и прямой (поверхностную плотность считать равной единице).

д) С помощью двойного интеграла вычислить координаты центра тяжести фигуры, ограниченной линиями (поверхностную плотность считать равной единице).

Решение.

а) Сделаем чертеж, учитывая, что вершина параболоида находится в точке В(0; 0; 4), радиус окружности в плоскости хОу равен , осью цилиндраявляется осьОz, радиус поперечного сечения равен 2, а уравнение описывает координатную плоскостьхОу.

z

4 В

2 2у

3

х

Объем полученного тела найдем через тройной интеграл по формуле

.

С учетом характера области интегрирования вычисления удобно вести в цилиндрических координатах.

Зависимость между декартовыми и цилиндрическими координатами точки имеет вид:

где угол равен углу между осьюОх (х>0) и ,ии .

z М(;;z)  z 0у  М х

Якобиан перехода от декартовых координат к цилиндрическим координатам

.

Для вычисления объема тела в цилиндрической системе координат справедлива следующая формула:

или

.

В нашем случае (см. чертеж) а находим из уравнения параболоида, учитывая цилиндрические координаты:

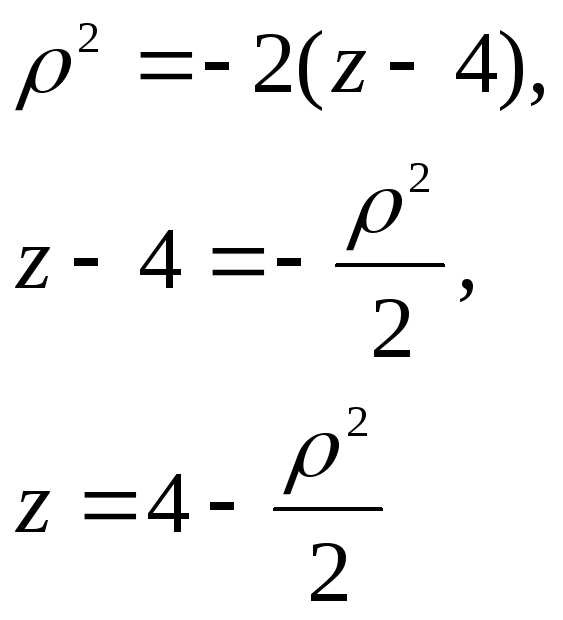
и, таким образом, .

С учетом вышесказанного имеем:

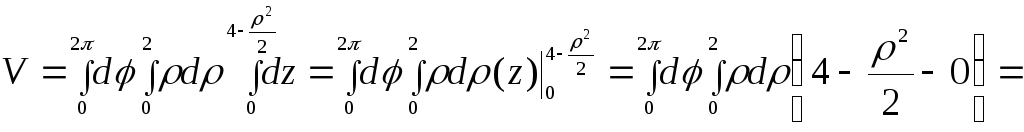
Ответ: ед³.

б) Сделаем чертеж, учитывая, что центр сферы находится в начале координат (0; 0; 0), радиус равен 3; осью вращения конуса является ось Оz, а угол между осью Оz и образующей конуса равен (так как каноническое уравнение конуса вращения , где – угол между образующей конуса и осью вращенияОz).

z

3

–3 3 у

3

х

С учетом характера области интегрирования вычисления удобно вести в цилиндрических координатах.

Зависимость между декартовыми и цилиндрическими координатами точки имеет вид:

где угол равен углу между осьюОх (х>0) и , уголравен углу между осьюОz (z>0) и ,и .

z М(;;r) r 0у  М х

Якобиан перехода от декартовых координат к цилиндрическим координатам

.

Для вычисления объема тела в сферической системе координат справедлива следующая формула:

.

В нашем случае (см. чертеж) и

Ответ: ед³.

в) Дан вектор поля и плоскостью . Для выполнения чертежа уравнение данной плоскости приведем к виду «в отрезках»:

Уравнения координатных плоскостей имеют вид:

.

z

3

–3

S₂S₄

S₁

0 6 y

S₃

х

Полная поверхность пирамиды

.

По формуле Остроградского–Гаусса

,

где .

В нашем случае у вектора поля

и.

(Значит, внутри пирамиды у векторного поля больше стоков, чем источников поля.)

Тогда поток векторного поля через поверхностьравен

,

где – объем пирамиды.

ед.³ и

.

Ответ: .

г) В случае однородной пластины, занимающей область плоскостихОу, координаты центра тяжести находят по формулам:

где – площадь области,

.

В рассматриваемом случае фигура ограничена кривыми ипри.

у

3

–5 0 5х

–3

Поэтому

Полученный интеграл вычислим заменой переменной.

Итак, . Далее

Первый из полученных интегралов вычисляется с помощью замены переменной:

Отсюда

.

Наконец,

д)

у

3

–9 3 х

3

Поскольку фигура симметрична относительно оси Ох, то . Вычислим.

Таким образом, .

13. а) Вычислить работу, совершаемую переменной силой по контуру, связывающему точкиМ(1; 1) и N(2; 3) и установить независимость от пути интегрирования;

б) найти потенциал поля .

Решение. а) Для того, чтобы найти работу, совершаемую переменной силой вычислим криволинейный интеграл

по контуру, соединяющему точки М(1; 1) и N(2; 3).

Выберем в качестве контура интегрирования наиболее простой контур, связывающий точки М и N, например, ломаную, звенья которой параллельны осям координат.

у

3N

х= 2

у= 1

1М

0 1 2 х

Имеем на первом участке , на втором участке. Таким образом,

В данном случае выполнено условие независимости криволинейного интеграла от пути интегрирования

,

где ,. Действительно,.

б) Потенциал векторного поля находим по формуле

.

Для нашего случая

,

то есть потенциал данного поля равен

.

Проверим, правильно ли мы нашли потенциальную функцию. Для этого должны выполняться следующие условия:

.

В нашем случае:

по условию ,

по условию .

14. Найти вероятность безотказной работы участка цепи, если известно, что каждый -ый элемент работает независимо от других с вероятностью(= 1, 2, 3, 4, 5, 6)..

4

1

3

2

6

5

Решение. Участок цепи будет работать безотказно, если работают блоки 1–2 и 3–4–5–6 (последовательное соединение).

Рассмотрим блок 1–2. Элементы 1 и 2 соединены параллельно, следовательно, блок 1–2 будет работать, если хотя бы один из элементов 1, 2 исправен.

– надежность блока 1–2.

Рассмотрим блок 3–4–5–6. Блок 3–4–5–6 будет безотказно работать хотя бы в одном из случаев:

исправны элементы 3 и 4,

исправен элемент 5,

исправен элемент 6.

– вероятность безотказной работы блока 3–4.

–

надежность блока 3–4–5–6.

Следовательно,

– искомая надежность участка цепи.

15. Измерены диаметры для 60 деталей, обрабатываемых на некотором станке. Данные замеров приведены в табл. 1.

Таблица 1

70,88	67,04	69,20	66,24	64,80	71,52	67,52	68,96	67,36	68,64
67,12	66,96	69,04	66,00	66,00	64,88	65,84	67,52	65,68	70,00
70,80	66,32	67,40	66,08	69,76	68,01	65,76	69,20	65,60	66,72
67,44	67,72	68,72	64,00	66,32	68,21	70,96	67,76	66,88	69,12
65,84	64,88	69,46	68,48	65,04	70,00	70,16	68,72	67,04	69,36
66,48	68,20	64,72	70,40	67,76	69,28	71,20	67,90	66,80	70,24

Выполнить статистическую обработку результатов измерений по следующему плану:

1. Построить статистическое распределение выборки.

2. Выполнить точечные оценки среднего значения и дисперсиислучайной величины.

3. Построить гистограмму относительных частот, установив статистический (эмпирический закон распределения)

4. На том же чертеже построить кривую нормального распределения с параметрами и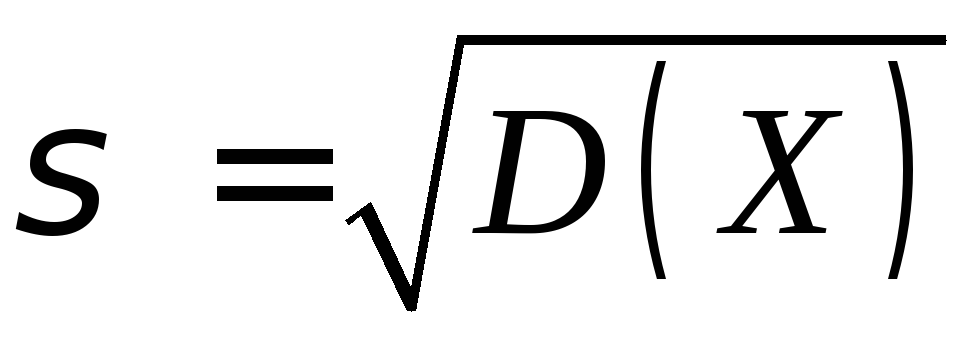и проанализировать, хорошо ли статистические данные описываются нормальным законом распределения