Reshenie tip priemov po matematike_ochnaya

Таким образом, точка х = 4 является для заданной функции точкой разрыва второго рода, а прямая х = 4 – вертикальной асимптотой графика.

3) Исследование на экстремум и промежутки монотонности.

у′

=

2х(х−4) −(х2 + 20)

=

х2

−8х−20

;

(х

−4)2

(х−4)2

х2 −8х−20

= 0;

(х−4)2

х2 −8х−20 = 0;

х1 = −2; х2 =10.

х

(−∞;−2)

–2

(–2; 4)

4

(4; 10)

10

(10;+∞)

f

′

+

+

–

не

–

0

+

(x)

сущ.

f

′

max

min

(x)

уmax = y(−2) = −4;

уmin = y(10) = 20 .

4) Исследование графика на выпуклость, вогнутость, точки пере-

гиба.

(2x −8)(x −4)2

−2(x −4)(x2 −8x −20)

y′′

=

=

(x −4)4

2(x −4)[(x − 4)2 −

=

(x2 −8x −20)]

=

36

.

(x − 4)4

(x

−4)3

Так как

y′′ ≠ 0 , то график заданной функции точек перегиба не имеет.

Остается выяснить вопрос об интервалах его выпуклости и вогнутости:

х

(−∞;−4)

4

(4;+∞)

f

′

–

не

+

(x)

сущ.

f

′

(x)

5) Исследование

графика

на

наличие

наклонных асимптот.

x

2

20

x2 + 20

1

+

f (x)

x2

k = lim

= lim

= lim

=1;

x

x

2

− 4x

x→∞

x→∞

x→∞

4

x2 1

−

x

x2

+ 20

4x + 20

b = lim ( f (x) − kx) = lim

− x = lim

= 4.

x→∞

x

− 4

x→∞ x −4

x→∞

54

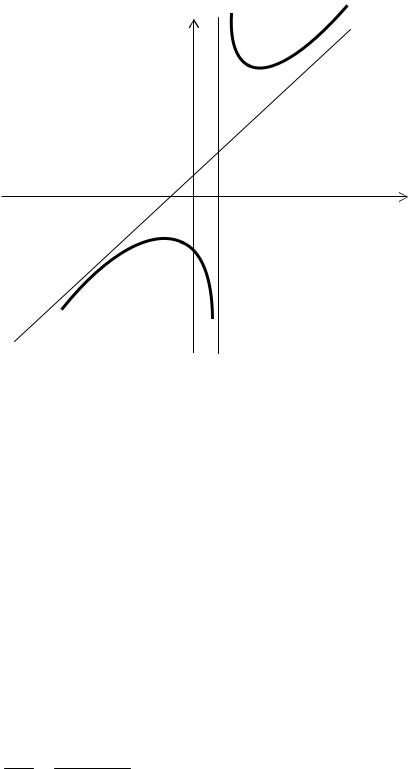
Таким образом, прямая y = x + 4 – наклонная асимптота графика.

6) График заданной функции пересекает ось Оу в точке (0; –5). По результатам исследования строим график.

у

20

4

–4

0 4

х

7. Резервуар, имеющий форму открытого сверху прямоугольного параллелепипеда с квадратным дном, нужно вылудить внутри оловом. Каковы должны быть размеры резервуара при его емкости 108 л воды, чтобы затраты на его лужение были наименьшими?

Решение. Затраты на покрытие резервуара оловом будут наименьшими, если при данной вместимости его поверхность будет минимальной.

Обозначим через а дм – сторону основания, b дм – высоту резер-

вуара. Тогда			площадь S его поверхности равна a2 + 4ab , а объем
V = a2b =108. Отсюда				432
b =	108		и S = a2 + 4ab = a2 +		.
	a2
				a

Полученное соотношение устанавливает зависимость между площадью поверхности резервуара S (функция) и стороной основания а (аргумент). Исследуем функцию S на экстремум. Найдем первую производную S′, приравняем ее к нулю и решим полученное уравнение:

S′ = 2a − 432 = 2a3 − 432 = 0 . a2 a2

Отсюда a = 6 . S′(a) > 0 при a > 6 , S′(a) < 0 при a < 6 . Следовательно, при a = 6 функция S имеет минимум. Если a = 6 , то b = 3. Таким обра-

55

зом, затраты на лужение резервуара емкостью 108 л будут наименьшими, если он имеет размеры 6 дм × 6 дм × 3 дм.

РАСЧЕТНО–ГРАФИЧЕСКАЯ РАБОТА №3

8. Построить кривые ρ =	9	в полярной системе коорди-
	5 − 4 cosϕ

нат.

Решение. Так как −1 ≤ cosϕ ≤1, то ρ > 0 при любом значении ϕ . Для каждого необходимого значения ϕ вычислим соответствующее зна-

чение			ρ . Например: если ϕ = 0,										то ρ =					9				= 9 ; если ϕ =			π		, то
																	5 − 4 cos 00								6
			9
ρ =							= 5,86. Результаты запишем в виде таблицы.
		5 − 4 cos			π
					6
ϕ	0			π			π	π		2π		5π		π		7π			4π	3π			5π	11π			2π
				6			3		2	3		6				6			3			2	3	6
ρ		9		5,86			3		1,8	1,29		1,06		1	1,06				1,29			1,8	3	5,86			9
		Построим кривую по полученным точкам.
							ϕ = π /2			ϕ = π /3								ϕ = π /6
																			ϕ = 0
									0		4					9				ρ

Запишем уравнение данной кривой в прямоугольной декартовой системе координат:

ρ =	9	,
	5 − 4 cosϕ

5ρ − 4ρ cosϕ = 9, 5ρ = 9 + 4ρ cosϕ.

56

Обе части этого равенства принимают положительные значения, возве-

дем их в квадрат: 25ρ2 = 81+ 72ρ cosϕ +16ρ2 cos2 ϕ .

Используем формулы:

x = ρ cosϕ, y = ρsinϕ, ρ2 = x2 + y2 ,

25(x2 + y2 )= 81+ 72x +16x2 ,
19x2 −72x + 25y2 = 81,
9(x2 −8x +16) + 25y2 = 225,
	(x − 4)	2	+	y2	=1 – уравнение эллипса.
25				9
С(4; 0) – центр эллипса, a = 5, b = 3 полуоси эллипса.
9. а) Решить систему двух линейных уравнений в области ком-
плексных			чисел			по	формулам	Крамера.	Найденные
z1, z2 , z = z1 + z2 , u = z1 − z2							изобразить на комплексной плоскости;
z1 и z2 , v = z1 z2 , w = z1 : z2							записать в показательной и тригонометри-
ческой формах;				найти 6 w ,			записать в показательной и алгебраической

формах и изобразить геометрически.

(1− j)z1 + 2z2 = 3 + j;2 jz1 + (−1+ j)z2 = − j.

Решение. Найдем решение системы линейных уравнений по фор-

мулам Крамера	z	=	∆1	,	z		=	∆2	. Для этого вычислим главный оп-
	1		∆			2		∆

ределитель системы ∆ и определители ∆1, ∆2 , учитывая, что z = x + jy

– комплексное число, где

j2 = −1

(j =

−1).

∆ =

1− j

2

= j − j4 = − j2;

j2

−1+ j

∆1

=

3 + j

2

= −3 + j2 −1+ j2 = −4 + j4;

− j

−1+ j

∆2

=

1− j

3 + j

= − j −1− j6 + 2 =1− j7.

j2

− j

Находим z1 и z2 :

z = ∆1

=

− 4 + j4

=

2

− 2 = −2 − j2

(т.к. 1

= − j );

j

1

∆

− j2

j

z2

=

∆2

=

1− j7

= −

1

1

+3

1

= 3,5 − j (−0,5) = 3,5 + j0,5.

− j2

2

2

∆

j

57

Таким образом, решение данной системы уравнений в алгебраической форме записи:

z1 = −2 − j2;

z2 = 3,5 + j0,5;

в векторной форме записи

z1 = (−2;−2);z2 = (3,5;0,5).

Для того, чтобы найти z = z1 + z2 в алгебраической форме, скла-

дываем действительные и мнимые части чисел z1 и z2 :

z = z1 + z2 = (−2 +3,5) + j(−2 + 0,5) =1,5 − j1,5.

Вектор, соответствующий числу z , строим как сумму векторов по пра-

вилу параллелограмма.

Для того, чтобы найти u = z1 − z2

в алгебраической форме, вычи-

таем действительные и мнимые части чисел z1 и z2 :

u = z1 − z2 = −2 − j2 −(3,5 + j0,5) = −2 −3,5 − j2 − j0,5 = −5,5 − j2,5.

Вектор, соответствующий числу u = z1 − z2 ,

записываем как сумму век-

торов

z1 и (−z2 ) и u = z1 + (−z2 )

, строим его по правилу параллело-

грамма.

у

–3,5

z2

– z2

ϕ

x

–2

0

3,5

и

z1

z

Найдем

модуль

r

и

аргумент

ϕ

комплексных

чисел z1 и z2

( r =

x2 + y2

или

r =

y

;

ϕ = arctg

y

в

1 и

4 четвертях;

sinϕ

x

ϕ = ±1800 + arctg xy во 2 и 3 четвертях, знак «+» или «–» выбираем так,

чтобы аргумент был наименьшим по модулю). Число z1 = −2 − j2 принадлежит 3 четверти:

1) ϕ = −1800	− 2		= −180	0 + 450 = −1350 (аргумент z );
	+ arctg
	− 2			1

58

2) sinϕ = sin(−					1350 )= −		2 ;
							2
	1				2
3)			=				2;
	sin	ϕ		1: −	2	= −
4) r = −2				1	= −2 (−		2)= 2 2 ≈ 2,83	(модуль z ).
				sin ϕ				1
	Число			z2 = 3,5 + j0,5 принадлежит 1 четверти:

1)ϕ = arctg 03,,55 = arctg 17 = 8,130 ;

2)sinϕ = sin 8,130 = 0,14;

3)sin1ϕ = 0,114 = 7,07;

4)r = 0,5 7,07 = 3,53.

		Запишем числа z и z					2	в показательной z = re jϕ	и тригонометри-
						1
ческой z = r(cosϕ + j sinϕ) формах:
z	= 2,83e− j1350 ,				z	= 2,83(cos(−1350 ) + j sin(−1350 ));
1					1
z2	= 3,53e j8,130 ,				z2	= 3,53(cos8,130 + j sin 8,130 ).
v = z		z	2	= 2,83e− j1350		3,53e j8,130 = 9,99e j(−1350 +8,130 ) = 9,99e− j126,870 ,
	1

v = 9,99(cos(−126,870 ) + j sin(−126,870 )),

так как при умножении комплексных чисел их модули перемножаются, а аргументы складываются.

w = z1 : z2 = 2,83e− j1350 : 3,53e j8,130 = 3,532,83e j(−1350 −8,130 ) = 0,8e− j143,130 ,

w = 0,8(cos(−143,130 ) + j sin(−143,130 )),

так как при делении комплексных чисел их модули делятся, а аргументы вычитаются.

Найдем 6 w = 6 0,8 е− j143,130 , используя формулу

ϕ+2mπ

n re jϕ = n r e n , где т = 0, 1, 2, …, п – 1.

В нашем примере п = 6, т = 0, 1, 2, 3, 4, 5 и мы получим 6 различных значений корня:

при т = 0

	0,8 еj	−143,130 +0	= 0,9635e− j240 = 0,9635(cos 240 − j sin 240 )=
w = 6		6
1

= 0,9635(0,914 − j0,405) = 0,88 − j0,39;

59

	при т = 1
w2	= 0,9635e j(−240 +600 ) = 0,9635e j360 = 0,9635(cos360 + j sin 360 ) =
= 0,9635(0,8 + j0,6) = 0,77 + j0,58;
	при т = 2
w	= 0,9635e j(−240 +2 600 )		= 0,9635e j960			= 0,9635(cos960 + j sin 960 ) =
3
= 0,9635(−0,1 + j0,99) = −0,096 + j0,95;
	при т = 3
w4	= 0,9635e j(−240 +3 600 )		= 0,9635e j1560			= 0,9635(cos1560 + j sin1560 ) =
= 0,9635(−0,914 + j0,405) = −0,88 + j0,39;
	при т = 4
w	= 0,9635e j(−240 +4 600 )		= 0,9635e j2160			= 0,9635e− j1440 = 0,9635(cos1440 −
5
− j sin1440 ) = 0,9635(−0,8 − j0,6) = −0,77 − j0,58;
	при т = 5
w	= 0,9635e j(−240 +6 600 )		= 0,9635e j2760			= 0,9635e− j840		= 0,9635(cos840 −
6
− j sin 840 ) = 0,9635(−0,1− j0,99) = 0,096 − j0,95
				w3		у
			w4			960	w2
			1560			360
					0	–240	x
			–1440			–840	w1
			w5
						w6
w	= 0,9635e− j240	= 0,88 − j0,39; w		2	= 0,9635e j360 = 0,77 + j0,58;
1
w	= 0,9635e j960	= −0,096 + j0,95;		w	4	= 0,9635e j1560		= −0,88 + j0,39;
3
w	= 0,9635e− j1440 = −0,77 − j0,58;			w		= 0,9635e− j840		= 0,096 − j0,95.
5					6

9. б) Найти скорость v (м/с) и ускорение а (м/с2) материальной точки, траектория которой задана параметрическими уравнениями

	х = 2	−3cos			π	t,
					6
			π
				t	+5
y = 9 cos			3

60

в момент времени t0				= 6 с.
	Решение.	Вектор rr(t) = x(t)i + y(t) j есть						радиус-вектор движу-
щейся материальной точки. В нашем случае										drr
r		π	r		π	t +5	r	r	=		есть вектор
r	(t) = 2 −3cos	6	t i	+ 9cos	3		j . Тогда вектор v			dt

скорости этой точки, который направлен по касательной к годографу данной линии в данной точке. В нашем случае

drr

−3cos

π

t

′r

π

t +5

′ r

3 π

sin

π

t

r

+

−

9 π

sin

π

r

dt

= 2

6

i

+ 9 cos

3

j

=

6

6

i

3

3

t j

t

t

drr

π π

r

π

r

r

π π

r

π

r

или

= 2 sin

6 t i

−3π sin 3 t

j;

v(t) =

2 sin 6 t i

−3π sin

3 t

j.

dt

В момент времени t0 = 6 с скорость материальной точки равна

drr

π

π

r

π

r

r

dr

r

dt

(6) =

sin

6

i −3π sin

6

j

или v(6)

=

(6) = −3π 1 j;

2

6

3

dt

vr(6 c) = −3πrj,

а величина скорости v =

vr(6 c)

=

−3πj

= 3π м/с.

Как известно, вектор ускорения движения материальной точки равен

r

d 2rr

dvr

r′

a

=

2

= dt (t) = v (t). В нашей задаче

r

dvdtr

r′

π

π

r

π

r

′

π

2

π

r

2

π

r

a

=

(t) = v (t) =

sin

t i

−3π sin

t

j

=

cos

t i

−π

cos

t j,

dt

2

6

3

12

6

3

t

r

=

π 2

cos

π

r

−π 2 cos

π

r

r

π

2

r

r

= −

π 2

r

−π

r

a

12

6

t i

3

t j

и a(6 c) =

12

(−1)i −π 2 1 j

12

i

2 j .

r

r

=

π 4

1

2

1

+1 =

π 2

145

.

a

= a

−

12

+π 4 (−1)2 =π2

144

12

10. а) Вычислить площадь фигуры, ограниченной заданными па-

раболами у = 2х2 − х−2;

у = −х2 + х−1.

б) Найти объем тела, образованного вращением вокруг оси Ох фигуры, расположенной в первом квадранте и ограниченной заданными

параболой у = 8х2 , прямой у = −6х+14 и осью Ох.

Решение.

а) Найдем абсциссы точек пересечения заданных парабол. Для этого приравняем правые части их уравнений:

2х2 − х−2 = −х2 + х−1.

Отсюда 3х2 −2х−1 = 0, D = 4 + 4 3 =16,

61

x1 = 2 +6 4 =1, x2 = 2 −6 4 = −13 .

у

1

–1

0

1

х

Площадь вычислим по формуле

											b
								S = ∫[f2 (x) − f1(x)]dx ,
											a
где f1(x) ,	f2 (x) – кривые, ограничивающие фигуру ( f2 (x) ≥ f1(x) ).
В нашем случае
S = ∫1 [(−x2 + x −1) −(2x2 − x − 2)]dx = ∫1 [−3x2 + 2x +1)]dx =
−	1														−	1
	3
										1			3
			x	3		x	2							34
= −3					+ 2			+ x					=		.
	3				2						1		27
										−
											3

б) Найдем абсциссу точки пересечения параболы и прямой в первом квадранте. Для этого решим уравнение

8х2 = −6х+14 ,

4х2 +3х−7 = 0 ,

х = −	7	,	х	2	=1.
1	4

Первому квадранту соответствует корень х2 =1.

Найдем теперь абсциссу точки пересечения прямой с осью Ох, ре-

шив уравнение −6х+14 = 0 , откуда х = 73 .

Таким образом, можно считать, что тело вращения ограничено при 0 ≤ х ≤1 поверхностью, образованной вращением параболы у = 8х2 во-

круг оси Ох, а при 1 ≤ х ≤ 73 – вращением прямой у = −6х+14 .

62

у

8

0 2 х

Объем ищем по формуле

		b	(f (x))2 dx .
		V =π∫
	7	a
V =π∫1 (8x2 )2 dx +π
	∫3	(−6x +14)2 dx .
0	1

Для вычисления второго интеграла используем подстановку t = −6x +14 .

Тогда dt = −6dx,										dx = −			1 dt	и
7													6
											0											0
														π			t3								256
π ∫3 (−6x +14)2 dx =π∫t 2dt = −																							=					π .
1											8			6	3							8	9
Отсюда																			1
1					2				256					х5									256						64		256		1856
V =π∫(8x				2	) dx +																														π .
									9		π =		64π	5							+		9				π =		5	π +	9	π =	45
0																			0
		11. а) Вычислить длину дуги кривой, заданной параметрическими
уравнениями
			=		(t	2	− 2)sin t + 2t cost,
		х														0 ≤ t								≤π.
					(2 −t			2	)cost + 2t sin t,
			=
		y

Решение. Длина дуги кривой, заданной параметрическими уравнениями, вычисляется по формуле

t2

l = ∫ (xt′)2 + (yt′)2 dt .

t1

Находим xt′ и yt′ для рассматриваемой кривой:

63