Reshenie tip priemov po matematike_ochnaya

−2x + y + 2z = 6,

−26x + 6y + 26z =1,

S4 : − 3x + 6y + 3z =1.

Уравнения координатных плоскостей имеют вид:

S1 : z = 0, S2 : y = 0, S3 : x = 0 .

z

3

S2		–3	S4
	S1
0	6		y
		S3

х

Полная поверхность пирамиды

S = S1 + S2 + S3 + S4 .

По формуле Остроградского–Гаусса

П = ∫∫(Fr nr0 )ds =∫∫∫divFdv ,

S V

где divFr = ∂∂Px + ∂∂Qy + ∂∂Rz .

В нашем случае у вектора поля F = Pi +Qj + Rk

P = 0, Q = x − 2y +5z, R = 0 и divF = 0 + (−2) + 0 = −2 < 0 .

(Значит, внутри пирамиды у векторного поля больше стоков, чем источников поля.)

Тогда поток векторного поля F через поверхность S равен

П = ∫∫∫(−2)dv = −2∫∫∫dv = − 2 V ,

V

V

где V – объем пирамиды.

V =

1

Sосн H =

1

1

6

−3

3 = 9 ед.3

и

3

3

2

П = −2 9 = −18.

Ответ: П = −18.

24. Найти циркуляцию векторного поля F = (x − 2y +5z) rj вдоль

линии пересечения

L

плоскости S4 : −2x + y + 2z −6 = 0 с координат-

ными плоскостями непосредственно и по формуле Стокса (точка пробе-

84

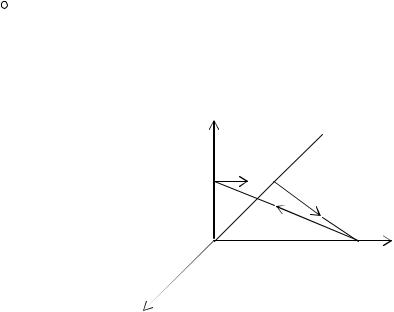
гает полученную линию против часовой стрелки, если смотреть от начала координат).

Решение. 1) Вычислим циркуляцию F по контуру L непосредст-

венно по формуле		r	r	r		r
r	r				+
Ц = ∫Fdr =		∫Fdr		+ ∫Fdr		∫Fdr,
L		AB		BC		CA
r r	∫Pdx +Qdy + Rdz.
∫Fdr =
AB	AB
						z
						С 3	3 А
									В
						0			6 у
				х
В нашем случае			P = R = 0, Q = x − 2y +5z						и уравнение АВ: z = 0,

− 2x + y = 6 , откуда y = 6 + 2x и dz = 0, dy = 2dx , причем x [−3;0]. Поэтому

r

r

0

0

0

∫Fdr

=

∫(x −12 − 4x)2dx =2 ∫(−3x −12)dx = −6 ∫(x + 4)dx =

AB

−3

−3

−3

2

0

9

15

x

4x

= −6

−

= −6

0 −

+12

= −6

= −45.

2

2

2

−3

ВС: x = 0 , y + 2z = 6 , y = 6 − 2z и dx = 0, dy = −2dz , и z [0;3].

r

r

=

3

0

∫Fdr

∫(x − 2y +5z)dy =∫(−12 + 4z +5z)(−2)dz = −6 ∫(3z − 4)dz =

BC

DC

0

−3

2

3

27

3

3z

− 4z

= −6

−

12

= −6

= −9.

= −6

2

2

2

0

СА: y = 0, dy = 0 .

r

r

= ∫(x − 2y +5z)dy = 0 .

∫ Fdr

CA

CA

Окончательно Ц = −45 −9 = −54 .

85

2)Вычислим циркуляцию по формуле Стокса.

Ц= ∫∫(rotFr nr0 )ds , где S = S1 + S2 + S3

(S : z = 0, nrS0 = −kr; S

2

: y = 0, nr0 = − j; S

3

: x = 0, nr0

= i ).

1

Предварительно найдем ротор вектора F = (x − 2y

r

ir

rj

kr

∂

∂

∂

∂

∂

∂

r

r

rotF

=

= i

∂y

∂z

−

j

∂x

∂x

∂y

∂z

x −2y +5z

0

0

0

x −2y +5z

0

+5z) rj :

∂

∂z +

0

+ kr

∂

∂

= −5ir + kr.

∂x

∂y

0 x − 2y +5z

За

поверхность,

натянутую

на

контур,

берем

поверхность

S = S1 + S2

+ S3

. Тогда

r

r

r

r

r

r

r

r

Ц = ∫∫rotF

(−k )ds + ∫∫rotF

(− j)ds + ∫∫rotF i ds

= ∫∫(−5i

+ k ) (−k )ds +

S1 r

r

r

S2

r

r

r

S3

S1

+ ∫∫(−5i

+ k ) (− j)ds

+ ∫∫(−5i

+ k ) i ds = −∫∫ds + 0 −5∫∫ds = −σS1 −5σS3 =

S2

S3

S1

S3

= −

1

6 3 −5

1

6 3 = −9 − 45 = −54

2

(σS

2

– площадь ∆OAB , σS

3

– площадь ∆OBC ).

1

25. Дано векторное поле V = z 2i + (z 2 + 2y) j + (2xz + 2 yz)kr и точ-

ки M1 (2;2;−1) , M 2 (6;1;r1)

и M 3 (1;1;2) .

1) Показать, что поле V – потенциальное.

2) Найти потенциал U (x; y; z) , если известно, что U (0;0;0) = 30.

3) Найти работу поля между точками M1

и M 2 ,

M 2 и M 3 , M 3

и M1 и

найти циркуляцию по контуру M1 M 2 M 3 M1.

Решение. 1) Одним из признаков потенциального поля является

равенство нулю ротора вектора поля.

r

r

r

r

i

j

k

∂R

− ∂Q

∂R − ∂P

r

∂R −

∂P

=

∂

∂

∂

=

r

r

+

rotV

i

−

j

k

.

∂x

∂y

∂z

∂y

∂z

∂x

∂x

∂y

∂z

P

Q

R

В нашем примере P = z2 , Q = z2 + 2y, R = 2xz + 2yz и

86

r

ir

rj

kr

∂

∂

∂

∂

∂

r

rotV =

= i

∂y

∂z

−

∂x

∂y

∂z

z2

+ 2y

2xz + 2yz

z2

z2 + 2y

2xz + 2yz

− rj

∂

∂

+ kr

∂

∂

=

∂x

∂y

∂x

∂z

z2

2xz + 2yz

z2 + 2y z2 + 2y

r

r

r

= i (2z − 2z) −rj (2z −

2z) + k

(0 −0) = 0.

таким образом,

rotV = 0 и заданное векторное поле является потенци-

альным.

2) Для потенциального поля вектор поля V = gradU , где U – по-

тенциал поля, то есть

Vr = ∂∂Ux ir + ∂∂Uy rj + ∂∂Uz kr.

Потенциал поля U (x; y; z) находим по формуле

x

y

y

U (x; y; z) = ∫P(t;0;0)dt + ∫Q(x;t;0)

x=const dt + ∫R(x; y;t)

x=const dt .

0

0

0

y=const

y

z

z

x

y

y

t 2

t 2

t 2

U (x; y; z) = ∫0 dt + ∫2tdt + ∫(2xt + 2yz)dt = 2

+ 2x

+ 2y

+C =

.

2

2

2

0

0

0

0

0

0

= y2 + xz2 + yz2 +C.

Проверка:

∂U

= z2 = P,

∂U

= z2 + 2 y = Q,

∂U

= 2xz + 2 yz = R .

∂x

∂y

∂z

Из условия U (0;0;0) = 30 находим С:

30 = 0 + 0 + 0 +C,

C= 30

ипотенциал поля равен

U(x; y; z) = y2 + xz2 + yz2 +30.

3)Работа потенциального поля между точками M1 и M 2 равна

разности значений потенциала в конечной и начальной точках.

AM1M2 =U (M 2 ) −U (M1 ) = (12 + 6 12 +1 12 +30)−(22 + 2 (−1)2 + 2 (−1)2 +30)= = 8 −8 = 0,

AM2M3 =U (M 3 ) −U (M 2 ) = (12 +1 22 +1 22 + 30)−(8 +30)= 9 −8 =1,

AM3M1 =U (M1 ) −U (M 3 ) = (8 +30)−(9 +30)= −1.

87

Циркуляция потенциального поля V по замкнутому контуру

Ц = AM1M 2M3M1 = AM1M 2 + AM 2M3 + AM3M1 = 0 +1 −1 = 0 .

Проверили еще rодин признак потенциального поля: циркуляция потенциального поляr V вдоль любого замкнутого контура равна нулю.

Ответ: 1. rotV = 0 ,

2.U (x; y; z) = y2 + xz2 + yz2 +30,

3.AM1M 2 = 0, AM 2 M 3 =1, AM 3 M1 −1, Ц = 0.

26.Найти вероятность безотказной работы участка цепи, если известно, что каждый i -ый элемент работает независимо от других с ве-

роятностью pi (i = 1, 2, 3, 4, 5, 6).

p1 = 0,6, p2 = 0,7, p3 = 0,8, p4 = 0,5, p5 = 0,9, р6 = 0,7 .

		1				3				4
		2							5
									6

Решение. Участок цепи будет работать безотказно, если работают блоки 1–2 и 3–4–5–6 (последовательное соединение).

Рассмотрим блок 1–2. Элементы 1 и 2 соединены параллельно, следовательно, блок 1–2 будет работать, если хотя бы один из элементов 1, 2 исправен.

Р1−2 =1 −(1 − р1 )(1 − р2 ) =1 − 0,4 0,3 = 0,88 – надежность блока 1–2.

Рассмотрим блок 3–4–5–6. Блок 3–4–5–6 будет безотказно работать хотя бы в одном из случаев:

исправны элементы 3 и 4, исправен элемент 5, исправен элемент 6.

Р3−4 = р3 р4 = 0,8 0,5 = 0,4 – вероятность безотказной работы блока

3–4.

Р3−4−5−6 =1 − (1 − р3−4 )(1 − р5 )(1 − р6 ) =1 − (1 − 0,4)(1 − 0,9)(1 − 0,7) = 0,982

– надежность блока 3–4–5–6. Следовательно,

Р = Р1−2 Р3−4−5−6 = 0,88 0,982 = 0,864 – искомая надежность участка цепи.

88

27. Рабочий обслуживает четыре однотипных станка. Вероятность того, что любой станок в течение часа потребует внимания рабочего равна 0,6. Предполагая, что неполадки на станке независимы, найти вероятность того, что в течение часа потребуют внимания рабочего: 1) все четыре станка; 2) ни один станок; 3) по крайней мере один станок.

Решение. Обозначим через А1, А2 , А3 , А4 события, состоящие в

том, что в течение часа потребуют внимания рабочего соответственно первый, второй, третий, четвертый станки. По теореме умножения вероятностей независимых событий вероятность того, что в течение часа все станки потребуют внимания рабочего, то есть произойдут события и А1 ,

и А2 , и А3 , и А4 , вычислим по формуле

Р(А1 А2 А3 А4 )= Р(А1 )Р(А2 )Р(А3 )Р(А4 )= 0,6 0,6 0,6 0,6 = 0,1296.

Вероятность того, что в течение часа станок (любой) не потребует внимания рабочего, найдем по правилу вычисления вероятности противоположного события:

Р(А1 )= Р(А2 )= Р(А3 )= Р(А4 )=1−0,6 = 0,4 .

Следовательно, вероятность события В, состоящего в том, что ни один станок в течение часа не потребует внимания рабочего, то есть произойдут события и А1 , и А2 , и А3 , и А4 , равна

Р(В) = Р(А1 А2 А3 А4 )= Р(А1 )Р(А2 )Р(А3 )Р(А4 )= 0,4 0,4 0,4 0,4 = 0,0256 .

Событие, состоящее в том, что в течение часа по крайней мере один из четырех станков потребует внимания рабочего, и событие В являются противоположными. Поскольку Р(В) = 0,0256 , то

Р(В) =1− Р(В) =1−0,0256 = 0,9744 .

РАСЧЕТНО–ГРАФИЧЕСКАЯ РАБОТА №8

28. Заданы законы распределения двух независимых случайных величин Х и У

Х	–5	2	3	4		У	1	4
Р	0,4	0,3	0,1	0,2		Р	0,2	0,8

Найти математическое ожидание и дисперсию для случайной величины

Z = 2X −7Y .

Решение. Найдем математические ожидания и дисперсии случайных величин Х и У:

89

М(Х) = −5 0,4 + 2 0,3 +3 0,1+ 4 0,2 = −0,3,

М(У) =1 0,2 +8 0,8 = 3,4.

Напишем законы распределения для случайных величин Х 2 и У2 :

Х 2		25		4		9		16	У 2		1		16
Р		0,4		0,3		0,1		0,2	Р		0,2		0,8

Найдем математические ожидания для случайных величин Х 2 и У2 :

М(Х 2 ) = 25 0,4 + 4 0,3 +9 0,1+16 0,2 =15,3,

М(У2 ) =1 0,2 +16 0,8 =13,0.

Отсюда

D(X ) = M (X 2 ) −[M (X )]2 =15,3 −(−0,3)2 =15,21,

D(X ) = M (Y 2 ) −[M (Y )]2 =13,0 −3,42 =1,44.

Пользуясь свойствами математического ожидания и дисперсии, а также независимостью случайных величин Х и У, получаем

M (Z) = M (2X −7Y ) = 2M (X ) −7M (Y ) = 2 (−0,3) −7 3,4 = −24,4, D(Z) = D(2X −7Y ) = 4D(X ) + 49D(Y ) = 4 15,21+ 49 1,44 =131,4.

29. Станок-автомат изготавливает шарики. Шарик считается годным, если отклонение Х его диаметра от проектного размера по абсолютной величине меньше 0,9 мм. Считая, что случайная величина Х распределена нормально с нулевым математическим ожиданием и со средним квадратическим отклонением σ = 0,5 мм, найти, сколько процентов

годных шариков изготовляет станок-автомат.

Решение. Воспользуемся формулой для вычисления вероятности заданного отклонения нормально распределенной случайной величины Х от ее математического ожидания

Р(Х − а <δ )= 2Ф δ ,σ

где а = М(Х), σ = D(X ), Ф(х) – функция Лапласа (см. таблицу значе-

ний функции Лапласа).

По условию а = М(Х) = 0, σ = 0,5, δ = 0,9 , поэтому

Р(Х < 0,9)= 2Ф 00,5,9 = 2Ф(1,8) = 2 0,4641 = 0,9282 .

Таким образом, станок-автомат изготовляет 92,8% годных шариков.

90

k =1+3, 2 lg n

30. Измерены диаметры X для 60 деталей, обрабатываемых на некотором станке. Данные замеров приведены в табл. 1.

Таблица 1							71,52
	70,88		67,04	69,20	66,24	64,80		67,52	68,96	67,36	68,64
	67,12		66,96	69,04	66,00	66,00	64,88	65,84	67,52	65,68	70,00
	70,80		66,32	67,40	66,08	69,76	68,01	65,76	69,20	65,60	66,72
	67,44		67,72	68,72	64,00	66,32	68,21	70,96	67,76	66,88	69,12
	65,84		64,88	69,46	68,48	65,04	70,00	70,16	68,72	67,04	69,36
	66,48		68,20	64,72	70,40	67,76	69,28	71,20	67,90	66,80	70,24

Выполнить статистическую обработку результатов измерений по следующему плану:

1)Построить статистическое распределение выборки.

2)Выполнить точечные оценки среднего значения x и дисперсии D(X ) случайной величины X .

3)Построить гистограмму относительных частот, установив статистический (эмпирический закон распределения).

4)На том же чертеже построить кривую нормального распределения

с параметрами a = x и σ = D(X ) и проанализировать, хорошо ли

статистические данные описываются нормальным законом распределения.

Решение. 1) Построение статистического распределения выборки.

Данную выборку преобразуем в вариационный (интервальный ряд). Для этого диапазон изменения случайной величины X в выборке делим на k интервалов. Число интервалов k определяется по эмпирической формуле с округлением до ближайшего целого. В на-

шем случае объем выборки n = 60 , поэтому k =1+3, 2 lg 60 ≈ 6, 69 ≈ 7 . Ши-

рину каждого интервала можно вычислить по формуле ∆ = xmax − xmin , где

k

xmax и xmin – наибольший и наименьший элементы выборки. Величина ∆

должна выбираться с точностью выборки и округляться в сторону завышения.

∆ = 71,52 −64, 00 ≈1, 074 ≈1,08 7

Границы интервалов вычисляются по формулам

x0* = xmin

xi*+1 = xi* +∆ (i = 0,1, 2,...k −1)

Для каждого интервала i подсчитываем количество попавших в него элементов ni . Если элемент совпадает с границей двух соседних интер-

валов, то его следует отнести к интервалу с меньшим номером.

91

	Вычисляем относительные частоты интервалов Wi =	ni	(i =1, 2,...k ).
		n

На основании полученных результатов заполняем первые четыре столбца таблицы 2.

Таблица 2

№ интер-	Границы интер-	ni	Wi										Wi
							xi			ui
вала	валов
														∆
1	(64,00;65,08)	6	6/60			64,540				-3			0,09
2	(65,08;66,16)	8	8/60			65,620				-2			0,12
3	(66,16;67,24)	11	11/60			66,700				-1			0,17
4	(67,24;68,32)	12	12/60			67,780				0			0,19
5	(68,32;69,40)	11	11/60			68,860				1			0,17
6	(69,40;70,48)	7	7/60			69,940				2			0,11
7	(70,48;71,56)	5	5/60			71,020				3			0,08
2) Оценка среднего значения					и дисперсии D(X )							случайной ве-
				x

личины X .

Математическое ожидание можно оценить, взяв среднее арифметическое чисел из таблицы 1:

x = x1 + x2 +...xn . n

Исправленная дисперсия может быть вычислена по формуле

n

2

2

x2

+ x2 +...+ x2

D (X )=

(x2

), где x

− x

=

1

2

n

.

n −1

n

Эти формулы целесообразно использовать, если объем выборки невелик, или все статистические данные внесены в компьютер (например, в программу Excel). При выполнении расчетов вручную используется иная методика, которая требует меньших вычислений.

В случае выборки большого объема среднее значение случайной величины X удобно вычислить по формуле

k

≈ ∑

iWi

(1)

x

x

i=1

где

x*

+ x*

- середина соответствующего интервала.

xi =

i−1

i

2

Для дисперсии получаются формулы следующего вида:

D (X )

n

(

−

2 ), где

=

x2

x

n −1

=

W1

2 +W2

2 +...+Wn

2

x1

x2

xn

, (2)

x2

n

наконец,

исправленное

среднее

квадратическое

отклоне-

ниеσ (X )=

D(X ).

Дополнительного упрощения расчетов можно добиться, если перейти от величин xi к величинам ui по формуле

92

ui = xi ∆−c (3)

Величину c выберем следующим образом:

c = xk2 , если k – четное, c = x(k +1)2 , если k – нечетное.

При таком выборе формулы перехода величины ui будут принимать последовательные целые значения, близкие к нулю.

Пользуясь свойствами дисперсии и математического ожидания, можно получить формулы, выражающие x и D(X ) через соответствую-

щие характеристики случайной величины U , аналогичные формулам

(1,2).

Таким образом, при решении пункта 3 настоящей задачи будем действовать в следующем порядке

1. Вычислим значения xi = xi*−12+ xi* и запишем их в 5 столбец таблицы

2.

2.В нашем случае c = x4 = 67, 78 .

3.В 6 столбец таблицы 2 заносим числа –3, –2, –1, 0, 1, 2, 3, которые получаются из значений xi по формуле (3).

4.

Вычисляем

значения

и

D(X )

по

формулам

x

= ∆

u1n1 +u2n2 +...uk nk

+c =

x

n

=1,08 −3 6 −2 8 −1 11+0 12 +1 11+ 2 7 +3 5 +67, 78 ≈ 67, 69

60

2

2

2

2

D (X )=

n

∆2

u1 n1

+u2 n2

+...uk nk

−

(

−c)

=

x

n −

1

n

=

60 1,082

(−3)

2

6

+(−2)

2

8 +(

−1)

2

11+0

2

12 +1 11+ 2

2

7 +3 5

−

2

2

59

60

−(67,69 −67,78)2 )≈ 3,57

3) Построение гистограммы относительных частот. Гистограммой называется ступенчатая фигура, состоящая из пря-

моугольников, основаниями которых служат частичные интервалы длиной ∆, а высоты равны W∆i .

Высоты прямоугольников записываем в 7 столбец таблицы 2. Диаграмма, построенная по данным таблицы 2, показана на рисунке.

Если теперь середины верхних сторон прямоугольников соединить плавной линией, то эта линия будет аналогом плотности распределения случайной величины – эмпирическим законом распределения.

93