Reshenie tip priemov po matematike_ochnaya

Решение. Так как по условию x0 = 0 , то искомое частное решение

y(x) можно записать в виде:

y(x) = y(0) +

y′(0)

x +

y′′(0)

x2

+

y′′′(0)

x3 +...

1!

2!

3!

′

Из начальных условий уже известны y(0)

и y (0). Подставив эти значе-

′′

:

ния в заданное уравнение, вычислим y (0)

′′

= 0

0 −1+ e

0

= 0.

y (0)

Последовательно дифференцируя данное уравнение, будем иметь:

′′′

′

+ xy

′′

− y

′

+ e

x

= xy

′′

+ e

x

;

y (x) = y

y(IV ) (x) =

y′′+ xy′′′+ ex .

Теперь вычислим значения производных при x = 0 : y′′′(0) =1; y(IV ) =1.

Следовательно, y(x) =1+10! x + 20! x2 + 31! x3 + 41! x4 +... или

y(x) =1+ 16 x3 + 241 x4 +...

есть искомое частное решение.

18. б) Используя разложение подынтегральной функции в степен-

1

ной ряд, вычислить интеграл ∫2

dx

с точностью до 0,001.

1

1

0 3 1 + x2

1

Решение. ∫2

dx

=

∫2

(1+ x2 )−

dx .

3

0 3 1+ x2

0

Разложим подынтегральную функцию в степенной ряд. Для этого

используем ряд

m

m(m −1)

m(m −1)(m − 2)

m

2

3

(1+ x) =1+

1! x +

2!

x

+

3!

x

+...,

где −1 < x <1. Положим m = −1

и заменим х на x2 :

1

3

(1+ x2 )−

=1−

1

x2

+

2

x4 −

14

x6

+...

3

3

9

81

1

Так как отрезок интегрирования

0;

принадлежит области схо-

2

димости полученного ряда (−1;1) , то будем интегрировать почленно в указанных пределах:

74

1			1																x3		2x5		14x7				1
2	dx		2			1		x2 +	2	x4		14			x6											2
∫0 3 1+ x2		=	∫0	1	−						−					+... dx =		x −		+		−		+...				=
						3			9			81							9		45		567
																										0

=12 − 721 + 7201 − 362887 +...

Вполученном знакочередующемся ряде четвертый член по абсолютному значению меньше 0,001. Следовательно, требуемая точность будет обеспечена, если учитывать только первые три члена ряда.

1
2	dx		1		1		1		39
∫0 3 1+ x2		≈		−		+		=		= 0,4875.
			2		72		720		80

РАСЧЕТНО–ГРАФИЧЕСКАЯ РАБОТА №6

19. Дана функция двух переменных z = x2 − xy + y2 +9x −6y + 20. Найти:

1)экстремум функции z(x; y) ;

2)gradz в точке А(1; –2);

3)наибольшую скорость возрастания z(x; y) точке А(1; –2).

Решение. 1) Для отыскания экстремума функции z(x; y) предвари-

тельно найдем частные производные первого и второго порядка:

∂∂xz = z′x = (x2 − xy + y2 +9x −6y + 20)′x = 2x − y +9, ∂∂yz = z′y = (x2 − xy + y2 +9x −6y + 20)′y = −x + 2y −6.

Приравняем их к нулю и решим систему уравнений:
2x − y +9 = 0,			2x +9 = y,				y = 2x	+9,
		= 0,		+9)	−6	= 0,			−6	= 0,
− x + 2y −6			− x + 2(2x				− x + 4x +18
y = 2x	+9,	y =1,
	= 0,
3x +12		x = −4.

Решением системы является точка М(–4; 1). Точка М(–4; 1) называется подозрительной на экстремум. Найдем частные производные второго порядка в точке М:

75

∂2 z

′′

′

′

′

∂x2

= zxx

= (zx )

x

= (2x − y +9) x = 2,

∂2 z

′′

′

′

′

= 2,

∂y2

= z yy

= (z y )

y

= (− x + 2y −6) y

∂2 z

′′

′

′

′

y = (2x − y +9) y

= −1.

∂x∂y

= zxy

= (zx )

Из них составим определитель второго порядка

∂2 z

∂2 z

2 −1

∆ =

∂x2

∂x∂y

=

= 4 −1 = 3.

∂2 z

∂2 z

−1 2

∂x∂y

∂y2

Так как

∆ = 3 > 0 , то в точке М(–4; 1) есть экстремум. Производная

∂2 z

= 2

> 0 , а, значит, это точка минимума функции.

∂x2

2) Градиент функции z найдем по формуле:

gradz =

∂z r

∂z

r

∂x

i +

∂y

j ,

∂z

∂z

и

были найдены в пункте 1.

∂x

∂y

gradz = (2x − y +9)ir + (−x + 2y −6) j .

Градиент функции z в точке А(1; –2): r gradz(A) = (2 1−(−2) +9)i + (−1+ 2 (−2) −6) j =13i −11 j .

3) Наибольшая скорость возрастания функции равна модулю градиента:

gradz(A) = 132 + (−11)2 = 290 .

20. а) Найти объем	тела, ограниченного параболоидом
x2 + y2 = −2(z − 4) , цилиндром	x2 + y2 = 4 и плоскостью z = 0 (z ≥ 0) ,

через тройной интеграл, применяя цилиндрическую систему координат.

Решение.
Сделаем чертеж, учитывая, что	вершина параболоида
x2 + y2 = −2(z − 4) находится в точке В(0; 0;	4), радиус окружности в

плоскости хОу равен 2 2 , осью цилиндра x2 + y2 = 4 является ось Оz,

радиус поперечного сечения равен 2, а уравнение z = 0 описывает координатную плоскость хОу.

76

z

4 В

2

2 2

у

3

х

Объем полученного тела найдем через тройной интеграл по фор-

муле

V = ∫∫∫dv .
V
С учетом характера области интегрирования (V ) вычисления удобно
вести в цилиндрических координатах (ϕ; ρ; z).
Зависимость между декартовыми и цилиндрическими координа-
тами точки имеет вид:
x = ρ cosϕ,					z
y = ρ sinϕ,						М(ϕ; ρ; z)
						ρ z
z = z,					0
где угол ϕ равен углу между осью						у
Ох (х>0) и OM ′, ρ =		OM ′		и	ϕ	М′
′				х
z = M M и

0 ≤ϕ ≤ 2π, 0 ≤ ρ < +∞, −∞ < z < +∞.

Якобиан перехода от декартовых координат к цилиндрическим координатам

I = ρ .

Для вычисления объема тела в цилиндрической системе координат справедлива следующая формула:

V = ∫∫∫ρdϕdρdz

V

или

β	ρ2	z2
V = ∫dϕ ∫ρdρ ∫dz .
α	ρ1	z1

В нашем случае (см. чертеж) 0 ≤ϕ ≤ 2π, 0 ≤ ρ < 2, а z находим из уравнения параболоида, учитывая цилиндрические координаты:

77

ρ2 = −2(z − 4),

z −

4 = −

ρ2

,

z = 4 −

ρ2

2

2

и, таким образом,

2

0 ≤ z ≤ 4

−

ρ

.

2

С учетом вышесказанного имеем:

4−

ρ2

ρ

2

2π

2

2π

2

2π

2

ρ2

2

4−

2

=

−

−0

=

V = ∫dϕ∫ρdρ ∫dz = ∫dϕ∫ρdρ(z)

0

∫dϕ∫ρdρ 4

2

0

0

0

0

0

0

0

2π

2

ρ3

2π

ρ2

ρ4

2

2π

2π

= ∫dϕ∫

−

=

∫dϕ(2 4 − 2)

= 6 ∫dϕ =

4ρ −

2

dρ

= ∫dϕ 4

2

8

0

0

0

0

0

0

= 6ϕ

2π

=12π.

0

Ответ: V =12π ед3.

20. б) Найти объем тела, ограниченного сферой x2 + y2 + z 2 = 9 и

конусом x2 + y2 − z2 = 0

(z ≥ 0), через

тройной

интеграл,

применяя

сферическую систему координат.

Решение. Сделаем чертеж, учитывая, что центр сферы находится в начале координат (0; 0; 0), радиус равен 3; осью вращения конуса явля-

ется ось Оz, а угол между осью Оz и образующей конуса равен π4 (так

как каноническое уравнение конуса вращения x2 + y2 −tg 2α z2 = 0, где α – угол между образующей конуса и осью вращения Оz).

z

3

–3

3

у

3

х

78

С учетом характера области интегрирования (V ) вычисления удобно вести в цилиндрических координатах (ϕ;θ; r).

Зависимость между декартовыми и цилиндрическими координа-

тами точки имеет вид:
x = r cosϕ sinθ,
		z
y = r sinϕ sinθ,			М(ϕ; θ; r)
		θ
z = r cosθ,			r
где угол ϕ равен углу ме-
		0	у
жду осью Ох (х>0) и OM ′,
угол θ	равен углу между	ϕ	М′
осью	Оz (z>0) и OM ,	х

r = OM и 0 ≤ϕ ≤ 2π, 0 ≤θ ≤π, 0 ≤ r < +∞.

Якобиан перехода от декартовых координат к цилиндрическим координатам

I = r 2 sinθ .

Для вычисления объема тела в сферической системе координат справедлива следующая формула:

					β		θ						r
V = ∫∫∫r 2 sinθdϕdθdr = ∫dϕ ∫2sinθdθ ∫2 r 2dr .
	V				α		θ1						r1				π
В нашем случае (см. чертеж)								0 ≤ϕ ≤ 2π, 0 ≤θ ≤										, 0 ≤ r ≤ 3 и
	π					π										π	4
													3
2π	4		3	2π		4				r3				2π		4			27
V = ∫dϕ ∫sinθdθ			∫r 2dr = ∫dϕ ∫sinθdθ										= ∫dϕ∫sinθdθ							=
										3									3
0	0		0	0		0							0	0		0
		π
2π				2π		2								2			2π				2 − 2
		4
							−									9 ϕ		=18π					=
= 9 ∫dϕ(−cosθ)		0	== −9 ∫dϕ			2		1	= 1−					2			0				2
0	2)π.			0
= 9(2 −				2)π ед3.
Ответ: V = 9(2 −

21. а) С помощью двойного интеграла вычислить координаты центра тяжести фигуры (меньшей по площади), ограниченной эллипсом

	х2	+	у2	=1 и прямой	х	+	у	=1 (поверхностную плотность считать рав-
	25		9		5		3

ной единице).

Решение. В случае однородной пластины, занимающей область D плоскости хОу, координаты центра тяжести x, y находят по формулам:

79

где S

y = 53

x =	1	∫∫xdxdy, y =		1			∫∫ydxdy,
	S				S
		D					D
– площадь области D ,
S = ∫∫dxdy .
	D
В	рассматриваемом						случае фигура ограничена кривыми
					x
25 − x2 и y = 3 1			−				при 0	≤ x ≤ 5.
				5

у

3

														–5									0							5		х
																								–3
Поэтому							3
				5							25−x2					5
							5										3	25 − x2										x
S = ∫∫dxdy = ∫dx											∫dy = ∫																−					=
																									−3 1			5	dx
		D		0									x			0	5
							3 1−
												5
	3	5		2											3x2 5					3 5						2				15
=		∫ 25 − x									3x			−				=				∫		25 − x			dx −				.
	5				dx −										10					5										2
		0															0					0
Полученный интеграл вычислим заменой переменной.
							x = 5sin t														π											π
	5					dx = 5costdt
																					∫2		25 −25sin2 t 5costdt =15∫2 cos2 tdt =
3	∫	25 − x2 dx				= t1 = 0											= 3
5	0												π					5			0											0
						t2					=
													2
		π																		π
		2 1+ cos 2t							15							sin 2t							15
																				2
=15∫						dt =							t		+							=			π.
			2														2						4
		0									2									0
			S = 15	(π − 2) . Далее
Итак,
			4

80

											5		3				25−x2
		1						4					5
x	=		∫∫xdxdy =								∫xdx						∫dy =
		S						15(π − 2)
			D								0						1−		x
														3
																			5
=			4	5		3	x 25 − x2									−		x
	15(π − 2)			∫		5					−3x 1							5		dx =
				0
			4	5					2				4							5	x2
=				∫x 25 − x						dx	−
	25(π − 2)											5(π		−			2)			∫ x −	5	dx.
				0																0

Первый из полученных интегралов вычисляется с помощью замены переменной:

													z = 25 − x2
5													dz = −2xdx																0																		3					0
			25 − x2 dx												1																						1						1		z 2									125
∫x										= −							dz = xdx = −∫																		z					dz	= −											=				.
															2																						2						2			3									3
0																										25
													z1 = 25																																2							25
													z2 = 0
Отсюда																																							5
				4						125						4							x2												x3						20											10						10
x =															−																	−								=								−									=		.
			25(π −2)							3							5(π −2)								2										15							3(π − 2)											3(π − 2)					3(π −2)
																																							0
Наконец,
																								3
																					5					25−x2
			1													4								5
y =				∫∫ydxdy						=											∫dx						∫ydy =
			S									15(π − 2)
				D																	0											x
																								3 1−
																															5
				2	5					9																	x							2
=					∫							(25				− x2 )−9 1									−										dx =
	15(π − 2)								25
																											5
					0
				12					5x			2				x3				5				2
=															−						=								.
										2												π −2
	125(π −2)																3			0

21. б) С помощью двойного интеграла вычислить координаты центра тяжести фигуры, ограниченной линиями y2 = x +9, y2 = −3x +9 (поверхностную плотность считать равной единице).

81

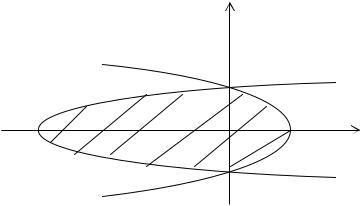
Решение.

у

3

–9

3

х

3

Поскольку фигура симметрична относительно оси Ох, то у = 0 . Вычис-

	лим x =							1			∫∫xdxdy .
							S
											D
																1	(9−у2 )
														3													3
																																1		(9 −			у2 )−(у2						−9)dу = 48;
	S = ∫∫dxdy = 2∫dу															3 ∫dх = 2∫
			D											0			у2 −9										0	3
								3			1		(9−у2 )								3											1	(9−у2 )										3
			1																	1						х2															1			1		(9 − у2 )2 − (у2 −9)2 dу =
	х =					2∫dу3								∫хdх =								∫									3						dу =						∫
			48																																						48
								0					у2 −9						24 0								2					у2 −9											0 9
				3																																										у3			3
		1						8																										1					8											12
	=			∫ −							у4		+16 у2 − 72 dу															=								−					у5		+16				− 72 у		= −			.
								9																										48				9	5							3				5
		48 0																																															0
	Таким образом, х = −2,4; у = 0 .
	r		22.								Вычислить											работу,															совершаемую										переменной силой
												r			3								r
	F	=	(x2 +3xy)i											+				x2	+ y j									по контуру, связывающему точки М(1; 1) и
															2
	N(2; 3), и установить независимость от пути интегрирования.
				Решение. Для того, чтобы найти работу, совершаемую переменной
					r													r			3													r
	силой F							= (x2 +3xy)i +																x2				+ y j , вычислим криволинейный интеграл
																					2
																					3
				А = ∫(x2 +3xy)dx +																							x2 + y dy
																					2

по контуру, соединяющему точки М(1; 1) и N(2; 3).

82

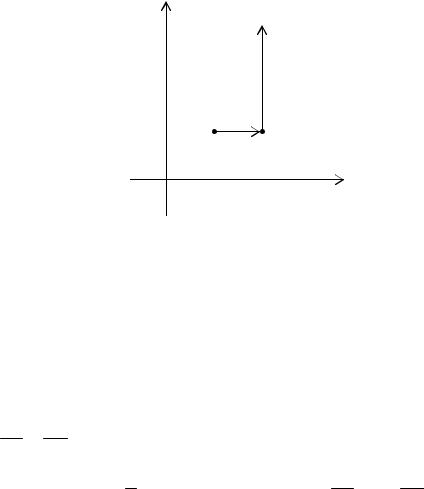
Выберем в качестве контура интегрирования наиболее простой контур, связывающий точки М и N, например, ломаную, звенья которой параллельны осям координат.

у		N
3
			х = 2
1	М	у = 1
0	1	2	х

Имеем на первом			участке	у =1, dy = 0, 1 ≤ x ≤ 2 ,										на	втором					участке
x = 2, dx = 0, 1 ≤ y ≤ 3. Таким образом,
2			3	x3				3x	2			2			y2			3			5
А = ∫(x	2						+							6y +					= 22			.
		+3x)dx + ∫(6 + y)dy =				3		2					+								6
1			1									1			2			1

В данном случае выполнено условие независимости криволиней-

ного интеграла от пути интегрирования

∂∂Py = ∂∂Qx ,

где P = x2 +3xy , Q = 23 x2 + y . Действительно, ∂∂Py = 3х, ∂∂Qx = 3х.

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №7

23. Найти поток векторного поля F = (x − 2y +5z) rj через полную поверхность пирамиды S , образованной данной плоскостью S4 : − 2x + y + 2z −6 = 0 и координатными плоскостями S1, S2 , S3 в направ-

лении внешней нормали к ее поверхности, применив теорему Остро- градского–Гаусса.

Решение. Дан вектор поля F = (x − 2y +5z) j и плоскостью − 2x + y + 2z −6 = 0 . Для выполнения чертежа уравнение данной плоскости приведем к виду «в отрезках»:

83