
Госы 5к Надя / ДУ / лекция 1
.docЛекция №1.
Тема: Дифференциальные уравнения первого порядка.
Вопросы:
1. Геометрические и физические задачи, приводящие к понятию дифференциального уравнения.
2. Основные понятия теории дифференциальных уравнений: дифференциальное уравнение, порядок ДУ, решение ДУ, интегральная кривая, начальные данные.
3. ДУ первого порядка. Нормальная форма записи. Понятия поля направлений и изоклин. Задача Коши и теорема Пикара. Общее, частное и особое решения ДУ.
В различных областях науки и техники часто встречаются задачи, для решения которых требуется решить одно или несколько уравнений, содержащих производные искомых функций. Рассмотрим несколько задач, приводящих к таким уравнениям.
Задача 1.
На плоскости хОу
найти кривую, проходящую через точку
![]() ,
у которой угловой коэффициент касательной,
проведенной в любой точке кривой, равен
удвоенной абсциссе точки касания.
,
у которой угловой коэффициент касательной,
проведенной в любой точке кривой, равен
удвоенной абсциссе точки касания.
Решение.
Пусть
![]() уравнение искомой кривой. По условию
задачи в каждой точке
уравнение искомой кривой. По условию
задачи в каждой точке
![]() существует касательная к этой кривой,
угловой коэффициент которой, т.е.
существует касательная к этой кривой,
угловой коэффициент которой, т.е.
![]() .
Таким образом, имеем
.
Таким образом, имеем
![]() . (1)
. (1)
Это уравнение содержит производную искомой функции. Уравнения такого типа, которые содержат производные искомой функции, называют дифференциальными уравнениями. Таким образом, наша задача свелась к нахождению функции, которая удовлетворяла бы дифференциальному уравнению (1), т.е. обращала бы это уравнение в тождество. Такая функция называется решением дифференциального уравнения, а процесс нахождения решений – интегрированием этого уравнения.
И з
уравнения (1) следует, что функция у
есть первообразная функции
з
уравнения (1) следует, что функция у
есть первообразная функции
![]() .
Следовательно,
.
Следовательно,
![]() ,
или
,
или
![]() , (2)
, (2)
где С – произвольная постоянная.
Из формулы (2)
следует, что дифференциальное уравнение
(1) имеет бесконечное множество решений,
т.е. уравнению (1) удовлетворяет не одна
кривая, а бесконечное множество кривых
- парабол. Чтобы из этого множества
кривых выбрать нужную нам кривую, нужно
воспользоваться тем, что искомая кривая
проходит через точку
![]() .
Следовательно, координаты этой точки
должны удовлетворять уравнению (2).
Поэтому
.
Следовательно, координаты этой точки
должны удовлетворять уравнению (2).
Поэтому
![]() ,
т.е.
,
т.е.
![]() .
Значит, искомая кривая
.
Значит, искомая кривая
![]() . (3)
. (3)
Искомая кривая
![]() является графиком решения дифференциального
уравнения (1). Она называется интегральной
кривой этого
уравнения.
является графиком решения дифференциального
уравнения (1). Она называется интегральной
кривой этого
уравнения.
Таким образом, интегральными кривыми уравнения (1) будут парабола (3) и все параболы (2), получающиеся из нее сдвигом вдоль оси ОУ на С единиц. Все эти параболы обладают одним общим свойством, выраженным дифференциальным уравнением (1): угловой коэффициент касательной равен удвоенной абсциссе точки касания.
Задача 2.
Найти закон движения свободно падающего
в пустоте тела, если пройденный путь
начинает отсчитываться от момента
времени
![]() и начальная скорость падания равна 0.
и начальная скорость падания равна 0.
Решение.
Скорость в этом случае выражается
формулой
![]() .
Как известно, скорость прямолинейного
движения равна производной от пути по
времени. Поэтому
.
Как известно, скорость прямолинейного
движения равна производной от пути по
времени. Поэтому
![]() . (4)
. (4)
Равенство (4) есть дифференциальное уравнение движения рассматриваемого тела. Оно задает закон движения в дифференциальной форме. Интегрируя уравнение (4), найдем интересующий нас закон движения в конечной форме.
Из уравнения (4)
следует, что функция
![]() является первообразной для функции
является первообразной для функции
![]() .
Следовательно,
.
Следовательно,
![]() или
или
![]() . (5)
. (5)
Выделим интересующее нас решение, в котором
![]() при
при
![]() . (6)
. (6)
Для этого положим
в формуле (5)
![]() ,
,
![]() .
Получим
.
Получим
![]() ,
откуда
,
откуда
![]() ,
следовательно, искомым решением
(движением) будет
,
следовательно, искомым решением
(движением) будет
![]() . (7)
. (7)
Формула (7) дает искомый закон движения тела. Других движений, определяемых дифференциальным уравнением (4) и условием (6), нет.
Условие (6) называется
начальным
условием, а
числа
![]() и
и
![]() - начальными
данными
решения (движения).
- начальными
данными
решения (движения).
В рассмотренных
двух задачах мы приходим к дифференциальному
уравнению вида
![]() .
Это уравнение является простейшим
дифференциальным уравнением. Однако в
большинстве случаев естественные и
технические процессы описываются более
общими и сложными дифференциальными
уравнениями. Дадим теперь определение
дифференциального уравнения и связанных
с ним общих понятий.
.
Это уравнение является простейшим
дифференциальным уравнением. Однако в
большинстве случаев естественные и
технические процессы описываются более
общими и сложными дифференциальными
уравнениями. Дадим теперь определение
дифференциального уравнения и связанных
с ним общих понятий.
Дифференциальное уравнение – это соотношение, связывающее между собой независимую переменную, искомую функцию и ее производные до некоторого порядка
![]() . (8)
. (8)
Порядок старшей производной, входящей в дифференциальное уравнение, называется порядком уравнения. Оба уравнения, рассмотренные нами в задачах 1 и 2, являются уравнениями первого порядка. Уравнения
![]() ,
,
![]() ,
,
![]()
являются соответственно уравнениями второго, третьего и четвертого порядков.
В теории
дифференциальных уравнений изучаются
и такие уравнения, которые содержат
несколько независимых переменных,
искомую функцию и частные производные
от искомой функции по независимым
переменным, например
![]() ,
,
![]() .
.
Такие уравнения называются уравнениями с частными производными. В отличие от них уравнения, в которых искомая функция является функцией только от одной независимой переменной, называются обыкновенными дифференциальными уравнениями.
Мы будем рассматривать главным образом уравнения, разрешенные относительно старшей производной, т.е. уравнения вида
![]() . (9)
. (9)
Относительно такого уравнения будем говорить, что оно задано в нормальной форме. Например, нормальной формой уравнения
![]()
будет
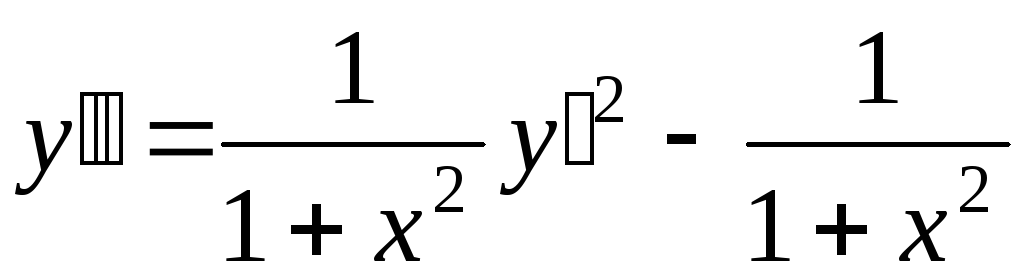 .
.
Всякая функция
![]() ,
определенная и непрерывная на некотором
множестве Х
вместе со своими производными до порядка,
равного порядку данного дифференциального
уравнения, и обращающая это уравнение
в тождество, справедливое при всех
значениях х
из этого множества, называется решением
этого дифференциального уравнения на
множестве Х.
Так, функция
,
определенная и непрерывная на некотором
множестве Х
вместе со своими производными до порядка,
равного порядку данного дифференциального
уравнения, и обращающая это уравнение
в тождество, справедливое при всех
значениях х
из этого множества, называется решением
этого дифференциального уравнения на
множестве Х.
Так, функция
![]() ,
,
![]() будет решением уравнения (8) на множестве
Х,
если
будет решением уравнения (8) на множестве
Х,
если
![]() ,
,
![]() .
Иногда решение получают в неявном виде
.
Иногда решение получают в неявном виде
![]() или в параметрической форме
или в параметрической форме
![]() ,
,
![]() (t
- параметр).
(t
- параметр).
График решения дифференциального уравнения называется интегральной кривой этого уравнения. Часто ради краткости интегральную кривую называют решением.
Рассмотрим следующий пример.
Пример 1. Функция
![]() ,
,
![]() (*)
(*)
является решением уравнения
![]() (**)
(**)
при
![]() (и во всяком конечном интервале), так
как
(и во всяком конечном интервале), так
как
![]() ,
,
![]() .
.
Дифференциальные уравнения первого порядка.
Согласно определению, данному выше, уравнение первого порядка имеет следующий вид:
![]() . (10)
. (10)
Будем рассматривать уравнения первого порядка в нормальной форме, т.е. разрешенные относительно производной от искомой функции:
![]() , (11)
, (11)
где функция
![]() определена и непрерывна в некоторой
области G
плоскости
определена и непрерывна в некоторой
области G
плоскости
![]() .
Напомним, что областью называется
непустое множество G
точек, обладающее следующими свойствами:
.
Напомним, что областью называется
непустое множество G
точек, обладающее следующими свойствами:
-
любая точка G – внутренняя, т.е. она имеет окрестность, целиком принадлежащую G;
-
множество G связно, т.е. любые две его точки можно соединить ломаной, целиком лежащей внутри G.
Установим связь между уравнением (11) и его интегральными кривыми. Пусть
![]() (12)
(12)
есть интегральная
кривая этого уравнения, проходящая
через точку
![]() .
Проведем касательную к интегральной
кривой (12) в точке М
и обозначим через
угол, образованный касательной МТ
с положительным направлением оси ОХ.
Тогда
.
Проведем касательную к интегральной
кривой (12) в точке М
и обозначим через
угол, образованный касательной МТ
с положительным направлением оси ОХ.
Тогда
![]() ,
но
,
но
![]() ,
поэтому
,
поэтому
![]() .
.
Таким образом,
если через точку
![]() проходит интегральная кривая (12), то
наклон касательной к ней в этой точке
определяется формулой
проходит интегральная кривая (12), то
наклон касательной к ней в этой точке
определяется формулой
![]() , (13)
, (13)
так что наклон касательной к интегральной кривой определен заранее самим дифференциальным уравнением.
Если в каждой точке области G задано значение некоторой величины, то говорят, что в области G задано поле этой величины.
Наклоны касательных можно указать, не находя интегральных кривых. Для этого построим в каждой точке М области G отрезок (для определенности – единичной длины) с центром в точке М, составляющий с положительным направлением оси ОХ угол , тангенс которого определяется формулой (13). Получим так называемое поле направлений, определяемое уравнением (11). Всякая интегральная кривая этого уравнения обладает тем свойством, что направление касательной в каждой ее точке совпадает с направлением поля, определяемым уравнением (11) в этой точке.
Направление поля
в точке
![]() задается функцией
задается функцией
![]() ,
где
,
где
![]() .
При построении поля направлений,
заданного формулой
.
При построении поля направлений,
заданного формулой
![]() ,
удобно использовать так называемые
изоклины,
т.е. линии, вдоль которых поле имеет одно
и то же направление. Изоклины поля
задаются равенствами
,
удобно использовать так называемые
изоклины,
т.е. линии, вдоль которых поле имеет одно
и то же направление. Изоклины поля
задаются равенствами
![]() .
.
Таким образом, дифференциальное уравнение (11) определяет поле направлений.
Тройка чисел
![]() определяет направление прямой, проходящей
через точку
определяет направление прямой, проходящей
через точку
![]() .
Совокупность отрезков этих прямых дает
геометрическую картину поля направлений.
.
Совокупность отрезков этих прямых дает
геометрическую картину поля направлений.
Задача интегрирования дифференциального уравнения (11) может быть истолкована следующим образом: найти такую кривую, чтобы касательная к ней в каждой точке имела направление, совпадающее с направлением поля в этой точке.
Пример.
Построим поле направлений, определяемое
уравнением
![]() .
.
Р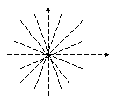 ешение.
Изоклины этого поля направлений задаются
равенством
ешение.
Изоклины этого поля направлений задаются
равенством
![]() ,
т.е.
,
т.е.
![]() ,
следовательно, являются прямыми,
проходящими через начало координат
(сама точка
,
следовательно, являются прямыми,
проходящими через начало координат
(сама точка
![]() выбрасывается из этих прямых, так как
при
выбрасывается из этих прямых, так как
при
![]() ,
,
![]() дробь
дробь
![]() не имеет числового значения). Для прямой
не имеет числового значения). Для прямой
![]() угловой коэффициент поля равен С,
т.е. совпадает с угловым коэффициентом
изоклины. Поэтому поле имеет вид,
изображенный на рисунке.
угловой коэффициент поля равен С,
т.е. совпадает с угловым коэффициентом
изоклины. Поэтому поле имеет вид,
изображенный на рисунке.
П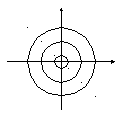 остроим
поле направлений для уравнения
остроим
поле направлений для уравнения
![]() .
.
Изоклины задаются
равенством
![]() ,
т.е. являются окружностями с центром в
начале координат. При
,
т.е. являются окружностями с центром в
начале координат. При
![]() получаем окружность нулевого радиуса,
т.е. точку
получаем окружность нулевого радиуса,
т.е. точку
![]() .
В этой точке
.
В этой точке
![]() и поэтому поле параллельно оси абсцисс.
На окружности
и поэтому поле параллельно оси абсцисс.
На окружности
![]() радиуса 1 имеем:
радиуса 1 имеем:
![]() ,
и поэтому поле образует угол
,
и поэтому поле образует угол
![]() с положительным направлением оси
абсцисс. Изобразим это поле направлений
и его изоклины.
с положительным направлением оси
абсцисс. Изобразим это поле направлений
и его изоклины.
Во многих задачах, которые приводят к дифференциальным уравнениям первого порядка, требуется найти решение, принимающее заданное значение при заданном значении независимой переменной. Такая задача называется начальной задачей или задачей Коши.
В общем виде для
уравнения первого порядка в нормальной
форме (11) задача
Коши ставится
так: требуется найти решение
![]() уравнения (11), удовлетворяющее начальному
условию (условию Коши)
уравнения (11), удовлетворяющее начальному
условию (условию Коши)
![]() при
при
![]() (
(![]() ).
При этом предполагается, что правая
часть уравнения (11) определена при
).
При этом предполагается, что правая
часть уравнения (11) определена при
![]() ,
,
![]() .
.
Геометрически
речь идет о нахождении интегральной
кривой, проходящей через заданную точку
![]() .
.
Для теории дифференциальных уравнений большое значение имеет вопрос о существовании решения задачи Коши и о единственности этого решения.
Теорема Пикара
(существования и единственности решения).
Пусть дано дифференциальное уравнение
(11), где функция
![]() определена и непрерывна в некоторой
окрестности начальной точки
определена и непрерывна в некоторой
окрестности начальной точки
![]() и
имеет непрерывную в этой окрестности
частную производную
и
имеет непрерывную в этой окрестности
частную производную
![]() ,
то уравнение (11) имеет единственное
решение
,
то уравнение (11) имеет единственное
решение
![]() ,
определенное в некоторой окрестности
точки
,
определенное в некоторой окрестности
точки
![]() и удовлетворяющее начальному условию
и удовлетворяющее начальному условию
![]() .
.
Теорема дает достаточные условия существования единственного решения задачи Коши для уравнения (11), но эти условия не являются необходимыми.
Пусть G
некоторая область на плоскости
![]() ,
через каждую точку которой проходит
одна и только одна интегральная кривая
уравнения (11). Функция
,
через каждую точку которой проходит
одна и только одна интегральная кривая
уравнения (11). Функция
![]() ,
определенная в некоторой области
изменения переменных х
и С
и непрерывно дифференцируемая относительно
х,
называется общим
решением
уравнения (11) в области G,
если она удовлетворяет двум условиям:
,
определенная в некоторой области
изменения переменных х
и С
и непрерывно дифференцируемая относительно
х,
называется общим
решением
уравнения (11) в области G,
если она удовлетворяет двум условиям:
1. равенство
![]() разрешимо в области G
относительно произвольной постоянной:
разрешимо в области G
относительно произвольной постоянной:
![]() ,
,
2. функция
![]() является решением уравнения (11) при всех
значениях произвольной постоянной
является решением уравнения (11) при всех
значениях произвольной постоянной
![]() ,
где
,
где
![]() произвольная точка области G.
произвольная точка области G.
Каждое решение,
получаемое из общего подстановкой
вместо С
конкретного числового значения,
называется частным
решением
уравнения. Особым
решением
называется решение
![]() ,
в каждой точке которого нарушается
единственность задачи Коши.
,
в каждой точке которого нарушается
единственность задачи Коши.
Пример. Рассмотрим уравнение
![]() . (14)
. (14)
Легко проверить,
что функция
![]() ,
где
,
где
![]() является общим решением этого уравнения
в верхней полуплоскости
является общим решением этого уравнения
в верхней полуплоскости
![]() .
Действительно,
.
Действительно,
![]() .
Всякое решение вида
.
Всякое решение вида
![]() ,
,
![]() является частным решением. В частности,
при
является частным решением. В частности,
при
![]() получаем частное решение
получаем частное решение
![]() ,
,
![]() .
Очевидно, что правая часть уравнения
(16) непрерывна во всей области определения
и ее частная производная по у
.
Очевидно, что правая часть уравнения
(16) непрерывна во всей области определения
и ее частная производная по у
![]() обращается в бесконечность только при
обращается в бесконечность только при
![]() ,
т.е. в точках оси ОХ.
Следовательно, только функция
,
т.е. в точках оси ОХ.
Следовательно, только функция
![]() может быть особым решением уравнения
(14). Чтобы эта функция действительно
была особым решением уравнения (14),
нужно, во-первых, чтобы она была решением
уравнения (14) и, во-вторых, чтобы в каждой
точке этого решения нарушалась
единственность решения задачи Коши.
Оба эти условия выполняются. Следовательно,
функция
может быть особым решением уравнения
(14). Чтобы эта функция действительно
была особым решением уравнения (14),
нужно, во-первых, чтобы она была решением
уравнения (14) и, во-вторых, чтобы в каждой
точке этого решения нарушалась
единственность решения задачи Коши.
Оба эти условия выполняются. Следовательно,
функция
![]() является особым решением уравнения
(14).
является особым решением уравнения
(14).
