Ведение в социально - экономическую статистику. Учебник. Новосибирск, 2004. 739 с

2.2. Средние величины

63

В финансовых расчетах аналогом темпа прироста капитала (величины типа запаса) выступает доходность на вложенный (инвестированный) капитал.

Пусть инвестированный капитал x0 в течение периода τ приносит доход ∆. Тогда капитал к концу периода становится равным x1 = x0 + ∆, и доходность капитала за этот период определяется как

δ= ∆ = x1 − 1, т.е. совпадает по форме с темпом прироста. x0 x0

Средняя за период доходность в зависимости от поведения инвестора (субъекта, вложившего капитал) рассчитывается различным образом. Ниже рассматривается три возможные ситуации.

1) Если позиция инвестора пассивна, и он не реинвестирует полученные доходы в течение данного периода времени, то средняя доходность в единицу времени определяется простейшим способом:

¯1 ∆

δ= τ x0 .

Фактически это — средняя арифметическая простая, т.к. ∆ x0 является общей доходностью за период времени τ . Такой способ расчета средней доходности наиболее распространен.

Эта формула используется и при τ < 1. Так, обычно доходности за разные периоды времени приводятся к среднегодовым, т.е. единицей времени является год. Пусть речь идет, например, о трехмесячном депозите. Тогда τ = 0.25, и среднегодовая доходность получается умножением на 4 доходности ∆ x0 за 3 месяца.

2) Пусть доходность в единицу времени ¯ в течение рассматриваемого периода вре-

δ

мени не меняется, но доходы полностью реинвестируются в начале каждой единицы

времени. Тогда за каждую единицу времени капитал возрастает в ¯ раз, и для

1 + δ

нахождения ¯ используется формула:

δ

	∆					∆	1
			¯ τ	¯			τ
1 +	x0	=	1 + δ	, т.е. δ =	1 +	x0	− 1.

Эта формула справедлива при целых положительных τ . Действительно (предполагается, что начало периода инвестирования имеет на оси времени целую координату), если τ < 1, ситуация аналогична предыдущей, в которой используется формула простой средней арифметической. Если τ не целое, то такая же проблема возникает для последней, неполной единицы времени в данном периоде.

¯	¯	τ				¯	(что следует из раз-
Естественно предположить, что δ < 1, тогда	1 + δ		> 1 + τ δ
ложения показательной функции в степенной ряд) и			1 ∆			¯
						> δ.
			τ x0

Это соотношение лучше интерпретировать «в обратном порядке»: если по усло-

виям инвестиционного контракта ¯ фиксирована и допускается реинвестирование

δ

64	Глава 2. Описательная статистика

доходов в течение периода, чем пользуется инвестор, то фактическая доходность на инвестированный капитал будет выше объявленной в контракте.

3) Пусть в течение данного периода времени доходы реинвестируются n раз через

равные промежутки времени. Тогда для ¯ справедлива следующая формула:

δ

	∆			¯ n
1 +		=	1 +	τ δ
	x0			n

(она совпадает с предыдущей в случае n = τ ).

Теоретически можно представить ситуацию непрерывного реинвестирования, когда n → ∞. В таком случае

	1		∆		¯
¯		ln 1 +		, поскольку lim	1 +	τ δ
δ =	τ		x0			n
				n→∞

n

¯

= eτ δ.

В соответствии с введенной ранее терминологией, это — непрерывный темп прироста в единицу времени. Данную формулу можно использовать при любом (естественно, положительном) τ .

Понятно, что средние доходности в единицу времени, полученные в рассмотренных трех случаях, находятся в следующем соотношении друг с другом:

1 ∆

∆

1

1

∆

τ

ln 1 +

> 1 +

− 1 >

.

τ x0

x0

τ

x0

пассивное

дискретное

непрерывное

поведение

реинвестирование

реинвестирование

Это соотношение при интерпретации в «обратном порядке» означает, что чем чаще реинвестируется доход, тем выше фактическая доходность на первоначальный капитал. В финансовых расчетах для приведения доходностей к разным единицам времени используется 1-я формула.

Теперь рассматривается общий случай с N + 1 моментом времени и расчетом средней доходности за N подпериодов.

1) Если позиция инвестора пассивна в течение всего периода времени, то средняя доходность в i-м подпериоде и в целом за период равны:

¯	1 ∆i			¯	1 ∆
δi =				, δ =				,
	τi x0				τ x0
N
где ∆i = xi − xi−1 , ∆ = i=1 ∆i = xN − x0 (τ					и τi определены выше). Средняя

доходность в целом за период удовлетворяет формуле средней взвешенной арифметической:

¯	¯	τi
δ =	αiδi, где αi =	τ	.

2.2. Средние величины

65

2) Пусть теперь доходы реинвестируются в начале каждого подпериода времени.

¯

¯

1

∆i

Тогда в течение i-го подпериода капитал вырастает в 1 + τiδi раз, где δi =

τ

x

.

i

i−1

Если предположить, что все подпериоды имеют одинаковую длину τ¯, то в среднем

за подпериод доход вырастает в

¯

1/N

раз, и это количество раз равно

1 + τ¯δi

¯

1 + τ¯δ. Поэтому

¯

1

¯

1/N

δ =

τ¯

1 + τ¯δi

− 1 .

Это формула простой средней приведенного выше общего вида f −1

1

f (xi) ,

N

где f = ln (1 + x).

Аналогичную формулу можно использовать и в случае подпериодов разной длины τi :

¯	1	¯	1		1
			N
δ =	τ¯	1 + τiδi		− 1 , где τ¯ =	N	τi.

Фактически эти формулы являются вариантами формул простой средней геометрической.

3) Пусть теперь все τi являются целыми положительными числами, и реинвестирование доходов происходит в начале каждой единицы времени. Тогда

¯	∆i	1 τi	¯	∆	1 τ
δi = 1 +	xi−1		− 1, δ = 1 +	x0	− 1.

Средняя в единицу времени доходность в целом за период равна средней взвешенной геометрической средних доходностей по подпериодам:

¯

¯ αi

τi

δ =

1 + δi

− 1, где αi =

τ

.

4) Наконец, в теоретическом случае непрерывного инвестирования

¯

1

∆i

¯

1

ln 1 +

∆

δi =

τ

ln 1 +

x

, δ =

τ

x

,

i

i−1

0

и средняя доходность за весь период, как и в первом случае, равна средней взвешенной арифметической средних доходностей по подпериодам:

¯	¯	τi
δ =	αiδi, где αi =	τ	.

В заключение этого раздела следует отметить, что особую роль в статистике играют средние арифметические. Именно они выступают важнейшей характеристикой распределения случайных величин. Так, в обозначениях предыдущего пункта величину x¯ = αixi можно записать как x¯ = xifi∆i или, при использовании теоретической функции плотности распределения, как x¯ = x f (x) dx.

(zl–1+∆l)

Рис. 2.8

zl

zl–1

x0.5

F1 0.5

Fl–1

66	Глава 2. Описательная статистика

Теоретическое арифметическое среднее, определенное последней формулой, называется в математической статистике математическим ожиданием. Математическое ожидание величины x обозначают обычно как E(x), сохраняя обозначение x¯ для эмпирических средних (см. Приложение A.3.1).

2.3. Медиана, мода, квантили

Мода и медиана, наряду со средней, являются характеристиками центра распределения признака. Медиана, обозначаемая в данном тексте через x0.5 , — величина (детерминированная), которая «делит» совокупность пополам. Теоретически она такова, что

x0.5	+∞
	f (x) dx = f (x) dx = 0.5,
−∞	x0.5

где f (x) — функция распределения (см. Приложение A.3.1).

По выборочным данным x1, . . . , xN , упорядочен-

ным по возрастанию, за нее принимается x(N +1)/2 в случае, если N нечетно, и (xN/2 + xN/2+1)/2, если N четно.

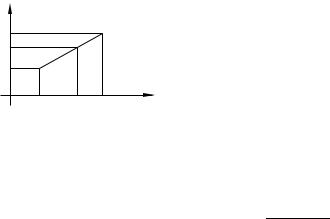
Значение медианы может быть уточнено, если по данным выборки построено эмпирическое распределение частот zl , l = 0, . . . , k, ∆l, αl, fl, Fl, l = = 1, . . . , k. Пусть l-й полуинтервал является медианным, т.е. Fl−1 < 0.5 Fl . Тогда, линейно интерполируя значения функции распределения F на этом

полуинтервале, медиану определяют по следующей формуле:

x0.5 = zl−1 + ∆l 0.5 − Fl−1 . αl

Ее смысл поясняется на графике (рис. 2.8). Этот график является фрагментом кумуляты.

o

Мода, обозначаемая в данном тексте через x, показывает наиболее вероятное значение признака. Это — значение величины в «пике» функции плотности распределения вероятности (см. Приложение A.3.1):

o

f x = max f (x).

x

2.3. Медиана, мода, квантили

67

Величины с унимодальным распределением имеют одну моду, полимодальные

распределения характеризуются несколькими модами. Непосредственно по вы-

борке, если все ее значения различны, величину моды определить невозможно.

Если какое-то значение встречается в выборке несколько раз, то именно его —

по определению — принимают за моду. В общем случае моду ряда наблюдений

находят по данным эмпирического распреде-

ления частот.

Пусть l-й полуинтервал является модаль-

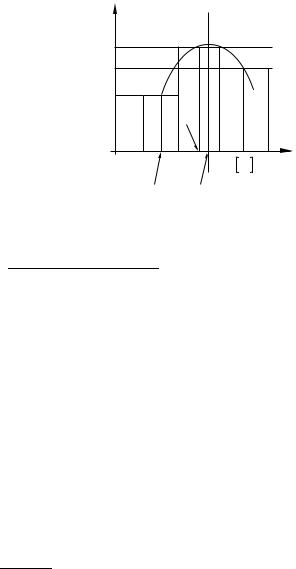
ным, т.е. fl > fl−1 и fl > fl+1 (во избежание

f1

непринципиальных уточнений случай « » не

fl+1

рассматривается). Функция плотности веро-

fl–1

ятности аппроксимируется параболой, прохо-

x1

дящей через середины ступенек гистограммы,

и ее максимум определяет положение искомой

моды. График (рис. 2.9) поясняет сказанное.

z

z

z

1

–

z

l–2

l–1

l

x2

l+1

2 –

m22

В случае если размеры полуинтервалов ∆l−1,

x2

x–

o

∆l и ∆l+1 одинаковы и равны ∆, такая про-

x

цедура приводит к определению моды по фор-

Рис. 2.9

муле:

o

fl − fl−1

x= zl−1 + ∆

.

(fl − fl−1) + (fl − fl+1)

В справедливости этой формулы несложно убедиться. Действительно, коэффициенты a, b и c аппроксимирующей параболы ax2 + bx + c удовлетворяют следующей системе уравнений:

ax¯2l−1 + bx¯l−1 + c = fl−1,

a(¯xl−1 + ∆)2 + b(¯xl−1 + ∆) + c = fl, a(¯xl−1 + 2∆)2 + b(¯xl−1 + 2∆) + c = fl+1.

Если из второго уравнения вычесть первое, а затем третье, то получится более простая система из двух уравнений:

∆(a(2¯xl−1 + ∆) + b) = fl − fl−1, ∆(a(−2¯xl−1 − 3∆) − b) = fl − fl+1.

Первое из этих уравнений дает выражение для b через a :

	b =	fl − fl−1	−	a (2¯x	l−1	+ ∆),
		∆

а их сумма — выражение для определения параметра a :

−2a∆2 = (fl − fl−1) + (fl − fl+1).

68	Глава 2. Описательная статистика
	Очевидно, что a отрицательно, и поэтому парабола имеет максимум в точке −b 2a
	o	−b 2a , и после подстановки
	(в этой точке производная 2ax + b равна нулю), т.е. x=
	сюда полученных выражений для b и a, учитывая, что x¯		+	∆	= z		, получается
		l−1		2		l−1

искомая формула.

Все три характеристики центра распределения: мода, медиана, среднее — находятся в определенных соотношениях между собой.

В случае идеальной (теоретически) симметрии

f (x0.5 + ∆) = f (x0.5 − ∆)

(2.5)

при любом ∆ 0, все эти три характеристики совпадают.

Доказательство этого утверждения проводится для теоретической функции плотности распределения f (x), в предположении, что она является гладкой, т.е. непрерывной и непрерывно дифференцируемой.

Дифференцирование выражения (2.5) по ∆ в точке 0 дает условие f (x0.5) = = −f (x0.5), из чего, в силу непрерывной дифференцируемости f , следует равенство нулю производной в точке x0.5. И поскольку распределение унимодально, то мода совпадает с медианой.

Теперь доказывается совпадение математического ожидания с медианой. Для случайной величины x −x0.5 с той же функцией распределения плотности f (x), в силу

+∞

того, что f (x) = 1, имеет место следующее тождество:

−∞

+∞

E (x) − x0.5 = (x − x0.5) f (x) dx.

−∞

Его правая часть разбивается на два слагаемых и преобразуется следующим образом:

x0.5	+∞
E(x) − x0.5 =	(x − x0.5) f (x) dx + (x − x0.5) f (x) dx =
−∞	x0.5

(в первом слагаемом производится замена переменных x − x0.5 = −∆ и переста-

0	+∞
новка пределов интегрирования	→ − , во 2-м слагаемом — замена пере-
+∞	0
менных x − x0.5 = ∆)
+∞	+∞
= − ∆f (x0.5 − ∆) d∆ + ∆f (x0.5 + ∆) d∆ =
0	0

2.3. Медиана, мода, квантили	69
(вводя соответствующие обозначения)
= −A− + A+.	(2.6)

Поскольку выполнено условие симметричности распределения (2.5), A− = A+ и математическое ожидание (среднее) совпадает с медианой. Это завершает рассмотрение случая симметричных распределений.

Для асимметричных распределений указанные три характеристики различаются, но так, что медиана всегда находится между средней и модой. При правой асимметрии

o

x < x0.5 < x,¯

при левой асимметрии, наоборот,

o

x¯ < x0.5 <x .

В этом легко убедиться. Пусть речь идет, например, о правой асимметрии. Распределение скошено в сторону больших значений случайной величины-признака, поэтому A− < A+ (это соотношение можно рассматривать в качестве определения правой асимметрии), и, в силу выполнения тождества (2.6), среднее должно превышать медиану: x0.5 < E(x), (x0.5 < x¯).

Условие A− < A+ может выполняться только в случае, если при достаточно больших ∆ имеет место неравенство f (x0.5 + ∆) > f (x0.5 − ∆) (веса больших значений признака больше, чем веса равноудаленных от медианы малых значений). Но тогда для малых ∆, т.е. в окрестности медианы, должно иметь место обратное

неравенство (поскольку	+∞	f (x0.5 − ∆) d∆ =	+∞	f (x0.5 + ∆) d∆ = 0.5):
	0		0

f (x0.5 − ∆) > f (x0.5 + ∆),

o

а это означает, что мода смещена влево от медианы: x < x0.5 .

Проведенное рассуждение о положении моды относительно медианы не является строгим, оно предполагает как бы «плавный» переход от симметрии к правой асимметрии. При строгом доказательстве существенную роль играет предположение об унимодальности распределения.

Случай левой асимметрии рассматривается аналогично.

Для больших выборок, как правило, подтверждается еще одно утверждение об относительном расположении трех рассматриваемых характеристик: при умеренной асимметрии мода удалена от медианы на расстояние приблизительно в 2 раза большее, чем среднее. То есть

o		≈ 2 | x¯ − x0.5 |.
x
	−x0.5

70	Глава 2. Описательная статистика

Для того чтобы легче запомнить приведенные здесь соотношения, можно использовать следующее мнемоническое правило. Порядок следования среднего, медианы и моды (при левой асимметрии) такой же, как слов mean, median, mode

ванглийском словаре (при правой асимметрии порядок обратный). Причем, как и соответствующие им статистические характеристики, слово mean расположено

всловаре ближе к median, чем mode.

Квантилем называют число (детерминированное), делящее совокупность в определенной пропорции. Так, квантиль xF (используемое в данном тексте обозначение квантиля) делит совокупность в пропорции (верхняя часть к нижней) 1 − F к F (см. Приложение A.3.1):

xF

P (x xF ) = F или F (xF ) = f (x) dx = F .

−∞

В эмпирическом распределении все границы полуинтервалов являются квантилями: zl = xFl . По данным этого распределения можно найти любой квантиль xF с помощью приема, использованного выше при нахождении медианы. Если l-й полуинтервал является квантильным, т.е. Fl−1 < F Fl , то

xF = zl−1 + ∆l F − Fl−1 . αl

Иногда квантилями называют только такие числа, которые делят совокупность на равные части. Такими квантилями являются, например, медиана x0.5 , делящая совокупность пополам, квартили x0.25, x0.5, x0.75 , которые делят совокупность на четыре равные части, децили x0.1, . . . , x0.9, процентили x0.01, . . . , x0.99 .

Для совокупностей с симметричным распределением и нулевым средним (соответственно, с нулевой модой и медианой) используют понятие двустороннего квантиля xˆF :

xˆF

P (−xˆF x xˆF ) = F (ˆxF ) − F (−xˆF ) = f (x) dx = F .

−xˆF

2.4.Моменты и другие характеристики распределения

Моментом q-го порядка относительно				c признака x называют величину
(q и c — величины детерминированные)
1			N	(xi − c)q ,
m (q, c) =		i=1
	N

2.4. Моменты и другие характеристики распределения		71
в случае, если она рассчитывается непосредственно по выборке;
k	k
m (q, c) =	αl (¯xl − c)q = fl (¯xl − c)q ∆l,
l=1	l=1

если используются данные эмпирического распределения частот;

+∞

µ (q, c) = f (x) (x − c)q dx = E((x − c)q )

−∞

—для теоретического распределения вероятности (cм. Приложение A.3.1).

Вэконометрии для обозначения теоретических или «истинных» значений величины (в генеральной совокупности) часто используются буквы греческого алфавита, а для обозначения их эмпирических значений (полученных по выборке) или их оценок — соответствующие буквы латинского алфавита. Поэтому здесь в пер-

вых двух случаях момент обозначается через m, а в третьем случае — через µ. В качестве общей формулы эмпирического момента (объединяющей первые два случая) будет использоваться следующая:

N

m (q, c) = αi (xi − c)q .

i=1

Впринципе, моменты могут рассчитываться относительно любых c, однако

встатистике наиболее употребительны моменты, рассчитанные при c, равном нулю или среднему. В первом случае моменты называют начальными, во втором — центральными. В расчете центральных моментов используются величины xi − x¯, которые часто называют центрированными наблюдениями и обозначают через xˆi .

Средняя является начальным моментом 1-го порядка:

x¯ = m (1, 0),

E (x) = µ (1, 0).

Благодаря этому обстоятельству центральные моменты при целых q всегда можно выразить через начальные моменты. Для этого надо раскрыть скобки (возвести в степень q) в выражении центрального момента.

Центральный момент 2-го порядка или 2-й центральный момент называется дисперсией и обозначается через s2 (эмпирическая дисперсия) или σ2 (теоретическая дисперсия):

s2 = m (2, x¯) ,

σ2 = µ (2, E (x)) .

72 Глава 2. Описательная статистика

При вычислении дисперсии иногда удобнее пользоваться начальным моментом 2-го порядка. Связь с ним устанавливается следующим образом:

s2 = αi (xi − x¯)2 = αix2i − 2¯x αixi +x¯2 =

←−−−→

x¯

= αix2i − x¯2 = m (2, 0) − m2 (1, 0) .

Корень квадратный из дисперсии — s или σ — является среднеквадратическим отклонением, иногда (главным образом, в англоязычной литературе) его называют стандартным отклонением.

Величины xˆi s называют центрированными и нормированными наблюдениями. Они измеряют значения признака в единицах среднеквадратического отклонения от среднего. Такая шкала измерения иногда называется стандартизованной

или стандартизированной.

Дисперсия (и среднеквадратическое отклонение) является мерой абсолютного рассеяния или разброса значений признака в совокупности. В принципе такой мерой мог бы служить 2-й момент относительно какого-то другого c, не равного x¯, но лежащего в центральной области распределения признака. Однако используют именно дисперсию, поскольку ее величина однозначно определена и, в некотором смысле, не зависит от c. Дисперсия минимальна среди всех 2-х моментов относительно c.

Действительно, производная 2-го момента по c

d (x − c)2f (x)dx	= −2 xf (x)dx − c f (x)dx = −2 (E(x) − c)
dc

равна 0 в точке c = E(x). Это точка минимума, поскольку 2-я производная по c

вней равна 2, т.е. положительна.

Встатистике используются и другие показатели разброса. Примерами показателей абсолютного разброса являются:

max xi − min xi — общий размах вариации,

2

x1−F − xF — квантильный размах вариации, где F < 0.5 (достаточно

2

часто используется квартильный размах вариации, то есть этот показатель при F = 0.25),

αi |xˆi| — среднее линейное отклонение.