Ведение в социально - экономическую статистику. Учебник. Новосибирск, 2004. 739 с

7.2. Основные гипотезы, свойства оценок

233

которой есть собственные вектора M −1 , Λ — диагональная матрица соответству-

ющих собственных чисел. Тогда

M −1 = Y ΛY = Y Λ0.5

Λ0.5Y

C

C

←−−−→←−−−→

(см. Приложение A.1.2).

√

Вектор случайных величин u =

N

C−1(a −α) обладает следующими свойствами:

σ

по построению E(u) = 0, и в силу того, что

(7.47) σ2

E ((a − α)(a −

α) ) =

M −1,

N

cov(u) = E (uu ) =

N

α) ) C −1

(7.49)

C−1E ((a

−

α)(a

−

= C−1M −1C−1

= I .

σ2

n

Следовательно, по определению χ2

случайная величина

u

u =

N

(a

−

α ) C −1C

−1 (a

−

α)

σ2

←−−−−−→

M

имеет указанное распределение (см. Приложение A.3.2).

Как было показано выше, e и a не коррелированы, поэтому не коррелированы случайные величины, определенные в (7.43, 7.48), и в соответствии с определением случайной величины, имеющей F -распределение:

N

a − α M (a

− α) (N

− n − 1)

e e

n

Fn, N −n−1.

σ2

σ2

Отсюда следует, что при нулевой гипотезе α = 0

a M a (N

−

n

−

1) (7.9) sq2 (N

−

n

−

1)

=

F

,

(e e)

se2n

n, N −n−1

N n

или

R2 (N − n − 1)

= F c

F

.

(7.50)

(1 − R2) n

n, N −n−1

Сама проверка нулевой гипотезы проводится по обычной схеме. Так, если значение вероятности pv статистики F c (величина, аналогичная sl для t-статистики) не превышает θ (например, 0.05), нулевая гипотеза отвергается с вероятностью ошибки θ, и модель считается корректной. В противном случае нулевая гипотеза не отвергается, и модель следует пересмотреть.

234	Глава 7. Основная модель линейной регрессии

7.3.Независимые факторы: спецификация модели

В этом пункте используется модель линейной регрессии в сокращенной форме, поэтому переменные берутся в центрированной форме, а m и M — вектор и матрица соответствующих коэффициентов ковариации переменных.

Под спецификацией модели в данном случае понимается процесс и результат определения набора независимых факторов. При построении эконометрической модели этот набор должен обосновываться экономической теорией. Но это удается не во всех случаях. Во-первых, не все факторы, важные с теоретической точки зрения, удается количественно выразить. Во-вторых, эмпирический анализ часто предшествует попыткам построения теоретической модели, и этот набор просто неизвестен. Потому важную роль играют и методы формального отбора факторов, также рассматриваемые в этом пункте.

В соответствии с гипотезой g2 факторные переменные не должны быть линейно зависимыми. Иначе матрица M в операторе МНК-оценивания будет необратима. Тогда оценки МНК по формуле a = M −1m невозможно будет рассчитать, но их можно найти, решая систему нормальных уравнений (6.14):

M a = m.

Решений такой системы нормальных уравнений (в случае необратимости матрицы M ) будет бесконечно много. Следовательно, оценки нельзя найти однозначно, т.е. уравнение регрессии невозможно идентифицировать. Действительно, пусть оценено уравнение

xˆ = zˆ1a1 + e,

(7.51)

где zˆ1 — вектор-строка факторных переменных размерности n1 , a1 — векторстолбец соответствующих коэффициентов регрессии, и пусть в это уравнение вводится дополнительный фактор zˆ2 , линейно зависимый от zˆ1 , т.е. zˆ2 = zˆ1c21 .

Тогда оценка нового уравнения

xˆ = zˆ1a1 + zˆ2a2 + e

(7.52)

(«звездочкой» помечены новые оценки «старых» величин) эквивалентна оценке уравнения xˆ = zˆ1 (a1 + a2c21) + e . Очевидно, что a1 = a1 + a2c21 , e = e , и, произвольно задавая a2 , можно получать множество новых оценок a1 = a1 − a2c21 .

Логичнее всего положить a2 = 0, т.е. не вводить фактор zˆ2 . Хотя, если из содержательных соображений этот фактор следует все-таки ввести, то тогда надо исключить из уравнения какой-либо ранее введенный фактор, входящий в zˆ1 . Таким образом, вводить в модель факторы, линейно зависимые от уже введенных, бессмысленно.

Рис. 7.1

7.3. Независимые факторы: спецификация модели		235
Случаи, когда на факторных переменных су-		A
ществуют точные линейные зависимости, встре-
чаются редко. Гораздо более распространена си-
туация, в которой зависимости между фактор-
ными переменными приближаются к линейным.
Такая ситуация называется мультиколлинеарно-	O
стью. Она чревата высокими ошибками получа-
емых оценок и высокой чувствительностью ре-
зультатов оценивания к ошибкам в факторных		C
переменных, которые, несмотря на гипотезу g2,
обычно присутствуют в эмпирическом анализе.		B

Действительно, в такой ситуации матрица M плохо обусловлена и диагональные элементы

M −1 , определяющие дисперсии оценок, могут принимать очень большие значения. Кроме того, даже небольшие изменения в M , связанные с ошибками в факторных переменных, могут повлечь существенные изменения в M −1 и, как следствие, — в оценках a.

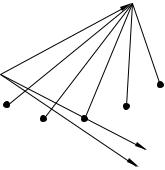
Последнее наглядно иллюстрируется рисунком (рис. 7.1) в пространстве наблюдений при n = 2.

На этом рисунке: OA — xˆ, OB — zˆ1 , OC — zˆ2 .

Видно, что факторные переменные сильно коррелированы (угол между соответствующими векторами мал).

Поэтому даже небольшие колебания этих векторов, связанные с ошибками, значительно меняют положение плоскости, которую они определяют, и, соответственно, — нормали на эту плоскость.

Из рисунка видно, что оценки параметров регрессии «с легкостью» меняют не только свою величину, но и знак.

По этим причинам стараются избегать ситуации мультиколлинеарности. Для этого в уравнение регрессии не включают факторы, сильно коррелированные с другими.

Можно попытаться определить такие факторы, анализируя матрицу коэффициентов корреляции факторных переменных S−1M S−1 , где S — диагональная матрица среднеквадратических отклонений. Если коэффициент sjj этой матрицы достаточно большой, например, выше 0.75, то один из пары факторов j и j не следует вводить в уравнение. Однако такого элементарного «парного» анализа может оказаться не достаточно. Надежнее построить все регрессии на множестве факторных переменных, последовательно оставляя в левой части уравнения эти переменные по отдельности. И не вводить в уравнение специфицируемой модели (с x в левой части) те факторы, уравнения регрессии для которых достаточно значимы по F -критерию (например, значение pv не превышает 0.05).

236	Глава 7. Основная модель линейной регрессии

AОднако в эмпирических исследованиях могут

возникать ситуации, когда только введение сильно

D коррелированных факторов может привести к построению значимой модели.

O

	Это утверждение можно проиллюстрировать ри-
	сунком (рис. 7.2) в пространстве наблюдений при
	n = 2.
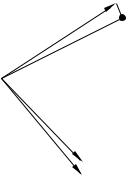
	На этом рисунке: OA — xˆ, OB — zˆ1 , OC —
C	zˆ2 , AD — нормаль на плоскость, определяе-
	мую векторами OB и OC , OD — проекция
B	OA на эту плоскость.

Рис. 7.2

Из рисунка видно, что zˆ1 и zˆ2 по отдельности

не объясняют xˆ (углы между соответствующими векторами близки к 90◦), но вместе они определяют плоскость, угол между которой и вектором OA очень мал, т.е. коэффициент детерминации в регрессии xˆ на zˆ1 , zˆ2 близок к единице.

Рисунок также показывает, что такая ситуация возможна только если факторы сильно коррелированы.

В таких случаях особое внимание должно уделяться точности измерения факторов.

Далее определяются последствия введения в уравнение дополнительного фактора. Для этого сравниваются оценки уравнений (7.51, 7.52) в предположении, что zˆ2 линейно независим от zˆ1 .

В этом анализе доказываются два утверждения.

1) Введение дополнительного фактора не может привести к сокращению коэффициента детерминации, в большинстве случаев он растет (растет объясненная дисперсия). Коэффициент детерминации остается неизменным тогда и только тогда, когда вводимый фактор ортогонален остаткам в исходной регрессии (линейно независим от остатков), т.е. когда

m		=	1	Zˆ e = 0	(7.53)
	2e
			N	2

(понятно, что коэффициент детерминации не меняется и в случае линейной зависимости zˆ2 от zˆ1 , но такой случай исключен сделанным предположением о линейной независимости этих факторов; в дальнейшем это напоминание не делается).

Для доказательства этого факта проводятся следующие действия.

Записываются системы нормальных уравнений для оценки регрессий (7.51, 7.52):

m1 = M11a1,

(7.54)

7.3. Независимые факторы: спецификация модели

237

m1

=

M11

m12

a1

,

(7.55)

m2

m21

m22

a2

где

m1 =

1

Zˆ Xˆ ,

m2 =

1

Zˆ Xˆ , M11 =

1

Zˆ Zˆ1 , m12

= m =

1

Zˆ Zˆ2 ,

N

1

N

2

N

1

21

N

1

1

m22

=

Zˆ Zˆ2 .

N

2

Далее, с помощью умножения обеих частей уравнения (7.51), расписанного по на-

блюдениям, слева на

1

Zˆ , устанавливается, что

N

2

(7.53)

(7.56)

m2 − m21a1

= m2e,

а из регрессии

ˆ

ˆ

Z2

= Z1a21 + e21 , в которой по предположению e21 = 0, находится

остаточная дисперсия:

1

(7.9)

− m21M11−1m12 > 0.

se221 =

e21e21

= m22

(7.57)

N

Из первой (верхней) части системы уравнений (7.55) определяется:

(7.54)

M11a1 + m12a2 = m1 = M11a1,

и далее

a1 = a1 − M11−1m12a2.

(7.58)

Из второй (нижней) части системы уравнений (7.55) определяется:

m22a2 = m2 − m21a1

(7.58)

− m21 a1 − M11−1m12a2 .

= m2

Откуда

m22 − m21M11−1m12 a2 = m2 − m21a1

и, учитывая (7.56, 7.57),

se221a2 = m2e.

(7.59)

Наконец, определяется объясненная дисперсия после введения дополнительного

фактора:

sq2

(7.9)

(7.58)

+ m2 − m1

(7.56)

= m1a1

+ m2a2

= m1a1

M11−1 m12 a2

= sq2 + m2ea2,

←−−→q

←−−−−→1

s2

a

(7.60)

238	Глава 7. Основная модель линейной регрессии
	т.е.
	sq2	(7.59)		m2
		= sq2	+	2e	.
				s2
				e21
	Что и требовалось доказать.
	Это утверждение легко проиллюстрировать рисунком 7.3 в пространстве наблюде-
	ний при n1 = 1.
	На этом рисунке: OA — xˆ, OB — zˆ1 ,		OC — zˆ2 , AD — нормаль xˆ на zˆ1
	( DA — вектор e).

Рисунок показывает, что если zˆ2 ортогонален e, то нормаль xˆ на плоскость, определяемую zˆ1 и zˆ2 , совпадает с AD, т.е. угол между этой плоскостью и xˆ совпадает с углом между xˆ и zˆ1 , введение в уравнение нового фактора zˆ2 не меняет коэффициент детерминации. Понятно также и то, что во всех остальных случаях (когда zˆ2 не ортогонален e) этот угол уменьшается и коэффициент детерминации растет.

	После введения дополнительного фактора zˆ2
	в уравнение максимально коэффициент детерми-	A
	нации может увеличиться до единицы. Это про-
	изойдет, если zˆ2 является линейной комбинацией
	xˆ и zˆ1 .
	Рост коэффициента детерминации с увеличе-	O
	нием количества факторов — свойство коэффи-		C
	циента детерминации, существенно снижающее	D	B
	его содержательное (статистическое) значение.
	Введение дополнительных факторов, даже если	Рис. 7.3

они по существу не влияют на моделируемую переменную, приводит к росту этого коэффициента. И, если таких факторов введено

достаточно много, то он начнет приближаться к единице. Он обязательно достигнет единицы при n = N − 1. Более приемлем в роли критерия качества коэффициент детерминации, скорректированный на число степеней свободы:

R˜2 = 1	−	1	−	R2	N	N − 1			1
						−	n	−

( 1 − R2 — отношение остаточной дисперсии к объясненной, которые имеют, соответственно, N − n − 1 и N − 1 степеней свободы), этот коэффициент может снизиться после введения дополнительного фактора. Однако наиболее правильно при оценке качества уравнения ориентироваться на показатель pv статистики F c.

Скорректированный коэффициент детерминации построен так, что он, так сказать, штрафует за то, что в модели используется слишком большой набор факторов. На этом же принципе построено и большинство других критериев, используемых

7.3. Независимые факторы: спецификация модели

239

для выбора модели: на них положительно отражается уменьшение остаточной дисперсии s2e (z1) (здесь имеется в виду смещенная оценка дисперсии из регрессии по z1 ) и отрицательно — количество включенных факторов n1 (без константы). Укажем только три наиболее известных критерия (из огромного числа предложенных в литературе):

Критерий Маллоуза:

C	= s2	(z	) +	2(n1 + 1)	sˆ2	(z),
p	e	1		N	e

где sˆ2e (z) — несмещенная оценка дисперсии в регрессии с полным набором факторов.

Информационный критерий Акаике:

AIC = ln 2πs2(z1) + 2(n1 + 1) .

e N

Байесовский информационный критерий (критерий Шварца):

2 ln(N )(n1 + 1)

BIC = ln 2πse (z1) + N .

В тех же обозначениях скорректированный коэффициент детерминации имеет вид

	R˜2 = 1	−	se2(z1)	N − 1	,
			se2( ) N − n1 − 1
где se2( ) — остаточная дисперсия из регрессии с одной константой.
					˜2	используется
Регрессия тем лучше, чем ниже показатель Cp ( AIC , BIC ). Для R
противоположное правило — его следует максимизировать. Вместо						˜	2	при неиз-
						R
менном количестве наблюдений N можно использовать несмещенную остаточную
дисперсию sˆ2	= sˆ2(z1), которую уже следует минимизировать.
e	e

В идеале выбор модели должен происходить при помощи полного перебора возможных регрессий. А именно, берутся все возможные подмножества факторов z1 , для каждого из них оценивается регрессия и вычисляется критерий, а затем выбирается набор z1 , дающий наилучшее значение используемого критерия.

˜2	2	при выборе моде-
Чем отличается поведение критериев R	( sˆe ), Cp , AIC , BIC

ли? Прежде всего, они отличаются по степени жесткости, то есть по тому, насколько велик штраф за большое количество факторов и насколько более «экономную» мо-

дель они имеют тенденцию предлагать. ˜2 является наиболее мягким критерием.

R

Критерии Cp и AIC занимают промежуточное положение; при больших N они ведут себя очень похоже, но Cp несколько жестче AIC , особенно при малых N . BIC является наиболее жестким критерием, причем, как можно увидеть из приведенной формулы, в отличие от остальных критериев его жесткость возрастает с ростом N .

Различие в жесткости проистекает из различия в целях. Критерии Cp и AIC направлены на достижение высокой точности прогноза: Cp направлен на минимизацию дисперсии ошибки прогноза (о ней речь пойдет в следующем параграфе),

240	Глава 7. Основная модель линейной регрессии

а AIC — на минимизацию расхождения между плотностью распределения по истинной модели и по выбранной модели. В основе BIC лежит цель максимизации вероятности выбора истинной модели.

2) Оценки коэффициентов регрессии при факторах, ранее введенных в уравнение, как правило, меняются после введения дополнительного фактора. Они остаются прежними в двух и только двух случаях: а) если неизменным остается коэффициент детерминации и выполняется условие (7.53) (в этом случае уравнение в целом остается прежним, т.к. a2 = 0); б) если новый фактор ортогонален старым ( zˆ1 и zˆ2 линейно не зависят друг от друга), т.е.

A

m		=	1	Zˆ	Zˆ	= 0	(7.61)
	12
			N	1	2

	(в этом случае объясненная дисперсия равна сумме	C
	дисперсий, объясненных факторами zˆ1 и zˆ2 по от-
		F
	дельности).	O
	Действительно, в соотношении (7.58) M11−1m12	D
		E
	не может равняться нулю при m12 = 0, т.к. M11
	невырожденная матрица. Поэтому из данного со-	B
	отношения следует, что оценки a1 не меняются,
	если a2 = 0 (случай «а») или/и m12 = 0 (случай	Рис. 7.4
	«б»).

Случай «а», как это следует из (7.59), возникает, когда выполняется (7.53).

В случае «б» соотношение (7.60) переписывается следующим образом:

sq2	(7.9)	a =a1	m1a1 + m2a2,
	= m1a1 + m2a2	1=

т.к. вторая (нижняя) часть системы (7.55) означает в этом случае, что m22a2 = m2 ,

т.е. a2	— оценка параметра в регрессии xˆ по zˆ2 :
	xˆ = zˆ a	2	+ e	2	= s2	+ s2	,	(7.62)
	2				q	q2
где s2	— дисперсия xˆ, объясненная только zˆ .
q2					2

Что и требовалось доказать.

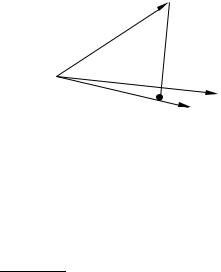
Иллюстрация случая «а» при n1 = 1 достаточно очевидна и дана выше. Рисунок 7.4 иллюстрирует случай «б». На этом рисунке: OA — xˆ, OB — zˆ1 , OC — zˆ2 ,

EA — e, нормаль xˆ на zˆ1 , F A — e2		, нормаль xˆ на zˆ2 , DA — e , нормаль
xˆ	на плоскость, определенную zˆ1 и zˆ2	, ED — нормаль к zˆ1 , F D — нормаль
к	zˆ2 .

Понятно (геометрически), что такая ситуация, когда точка E является одновременно началом нормалей EA и ED, а точка F — началом нормалей F A и F D, возможна только в случае, если угол COB равен 90◦.

7.3. Независимые факторы: спецификация модели

241

Но именно этот случай означает (как это следует из рисунка) одновременное выполнение соотношений регрессий (7.51) ( OE + EA = OA), (7.52) (при a1 = a1 ) ( OE +OF +DA = OA) и (7.62) ( OF +F A = OA), т.е. что введение нового фактора не меняет оценку при «старом» факторе, а «новая» объясненная дисперсия равна сумме дисперсий, объясненных «старым» и «новым» факторами по отдельности (сумма квадратов длин векторов OE и OF равна квадрату длины вектора OD).

	На основании сделанных утверждений можно
	сформулировать такое правило введения новых	A
	факторов в уравнение регрессии: вводить в ре-
	грессию следует такие факторы, которые имеют
	высокую корреляцию с остатками по уже введен-
	ным факторам и низкую корреляцию с этими уже	O
	введенными факторами. В этом процессе следует	D C
	пользоваться F -критерием: вводить новые фак-
	торы до тех пор, пока уменьшается показатель pv
	F -статистики.	B
	В таком процессе добавления новых факторов	Рис. 7.5
	в регрессионную модель некоторые из ранее вве-

денных факторов могут перестать быть значимыми, и их следует выводить из уравнения.

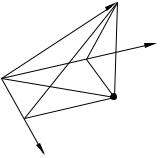
Эту возможность иллюстрирует рисунок 7.5 в пространстве наблюдений при n1 = 1.

На этом рисунке: OA — xˆ, OB— zˆ1 , OC — zˆ2 , AD — нормаль xˆ на плоскость, определенную zˆ1 и zˆ2 .

Рисунок показывает, что нормаль AD «легла» на вектор вновь введенного фактора. Следовательно, «старый» фактор входит в «новую» регрессию с нулевым коэффициентом.

Это — крайний случай, когда «старый» фактор автоматически выводится из уравнения. Чаще встречается ситуация, в которой коэффициенты при некоторых «старых» факторах оказываются слишком низкими и статистически незначимыми.

Процесс, в котором оценивается целесообразность введения новых факторов и выведения ранее введенных факторов, называется шаговой регрессией. В развитой форме этот процесс можно организовать следующим образом.

Пусть z — полный набор факторов, потенциально влияющих на x. Рассматривается процесс обращения матрицы ковариации переменных x, z, в начале которого рядом с этой матрицей записывается единичная матрица. С этой парой матриц производятся одновременные линейные преобразования. Известно, что если первую матрицу привести таким образом к единичной, то на месте второй будет получена матрица, обратная к матрице ковариации. Пусть этот процесс не завершен,

242	Глава 7. Основная модель линейной регрессии

и только n1 строк первой матрицы, начиная с ее второй строки (т.е. со строки первого фактора), преобразованы в орты; z1 — множество факторов, строки которых преобразованы в орты, z2 — остальные факторы. Это — ситуация на текущем шаге процесса.

В начале процесса пара преобразуемых матриц имеет вид (над матрицами показаны переменные, которые соответствуют их столбцам):

x

z1

z2

x z1

z2

mxx

m1

m2

1 0

0

m1

M11

M12

и

0 I1

0 ,

m2

M12

M22

0 0 I2

где

mxx =

1

Xˆ Xˆ — дисперсия x ,

N

m1 =

1

ˆ ˆ

— вектор-столбец коэффициентов ковариации z1

и x ,

N

Z1X

m2 =

1

ˆ ˆ

— вектор-столбец коэффициентов ковариации z2

и x ,

N

Z2X

M11 =

1

Zˆ

Zˆ1

— матрица коэффициентов ковариации z1

между собой,

N

1

M12 =

1

Zˆ

Zˆ2

— матрица коэффициентов ковариации z1

и z2 ,

N

1

M22 =

1

Zˆ2Zˆ2

— матрица коэффициентов ковариации z2

между собой.

N

На текущем шаге эти матрицы преобразуются к виду:

x

z1

z2

mxx − m1M1−1m1

m1M1−1

m2 − m1M1−1M12

←−−−−→1

←−−−−−−−−−−−−→e2

a

c

0

I1

0

m2 − M12M1−1m1

M12M1−1

M2 − M12M1−1M12

x

z1

z2

1

0

0

и

−M1−1m1

M1−1 −M1−1M12 .

0

0

I2