ТОЭ ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

Т11. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

СРАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

1.Общие определения

Параметры электрических цепей в той или иной мере всегда распределены вдоль длины отдельных участков. В большинстве практических случаев распределением параметров вдоль длины пренебрегают и представляют электрическую цепь эквивалентной схемой с сосредоточенными схемными элементами R, L и C.

Однако существует большой класс электрических цепей, для которых пренебрежение распределением параметров вдоль длины приводит к существенным погрешностям при их расчёте и становится неприемлемым.

Из курса физики известно, что электромагнитное поле распространяется вдоль электрической цепи не мгновенно, а с конечной скоростью υ,

проходя всю длину цепи l за время

Δt

l υ

. Если за время ∆t режимные па-

раметры в цепи (u, i) изменяются незначительно и этим изменением можно пренебречь, то для такой цепи пренебрегают распределением параметров вдоль длины и замещают ее схемой с сосредоточенными элементами. Если за время ∆t режимные параметры в цепи (u, i) изменяются на заметную величину, которую необходимо учитывать в расчете, то такие цепи считаются с распределенными параметрами и расчет их проводится уже с учетам распределения параметров вдоль их длины.

Пример 1. Воздушная линия электропередачи длиной l = 50 км рабо-

тает на частоте ƒ = 50 Гц, скорость волны υ = 300000 км/с, T

1

,

f

f

= 6000км, t

l

2 10

4

с,

t

360

t 3,6

. Таким образом,

фазовый

T

сдвиг для волн напряжения и тока вначале и в конце линии составляет всего 3,6о, чем можно пренебречь и считать такую линию как цепь сосредоточенными параметрами.

Пример 2. Линия электропередачи длиной l = 500 км: ƒ = 50 Гц, ско-

рость волны υ = 300000 км/с,

t	l	2 10	3
	υ

с,

t

	360	t
	T

36

.

Фазовый сдвиг для волн напряжения и тока в начале и конце линии составляет 36о, расчет режима в такой линии без учета распределения параметров по длине привел бы к существенным ошибкам, поэтому такую линию следует считать как цепь с распределенными параметрами.

Пример 3. Соединительный кабель от комнатной антенны до входного гнезда телевизора имеет длину l = 2 м, телевизионный канал работает на

181

частоте ƒ =

	t	l	10

150 МГц,

10	9	с,

υ = 200000

	t	360	t
		T

км/с,

540

	T	1
		f
	.

6,67 10	9

с,

f

1,3 м,

Вывод: соединительный кабель следует рассматривать как цепь с распределенными параметрами.

При синусоидальном режиме цепи критерием необходимости учета распределения параметров по длине может служить соотношение между длиной линии l и длиной волны . Если l << ,то цепь рассматривается

	как c сосредоточенными параметрами (в примере 1			l		50	0,0083 ), ес-
						6000
	ли l и		соизмеримы, то цепь рассматривается как с распределенными па-

раметрами (в примере 2

l

		500
		6000

0,083

, в примере 3

l

		2
		1,3

1,6

).

К цепи с распределенными параметрами относятся все лини связи, линии электропередачи длиной l > 100 км.

Одни и те же электрические цепи в зависимости от формы воздействующего напряжения в одних случаях принимаются с распределенными параметрами, а в других с сосредоточенными параметрами. Например, обмотки силовых трансформаторов при расчете установившихся режимов в них на частоте ƒ = 50 Гц считаются цепями с сосредоточенными параметрами, но при расчете переходных процессов, возникающих в результате коммутации или атмосферных разрядов те же обмотки считаются цепями с распределенными параметрами.

Если параметры цепи распределены равномерно по ее длине, то цепь называется, однородной, если неравномерно – то неоднородной. В курсе ТОЭ рассматриваются только однородные цепи.

2. Дифференциальные уравнения лини с распределенными параметрами

Рассмотрим двухпроводную однородную линию, физические параметры которой равномерно распределены по ее длине:

R0 – активное сопротивление пары проводов на единицу длины

[Ом/м], определяется по известной формуле

	R	l
		s

	1		l
			s

, зависит от мате-

риала провода (γ ) и от ее температуры	R R	(1 t)	;
	0

L0 – индуктивность пары проводов на единицу длины линии [Гн/м],

определяется как отношение потокосцепления к току ( L0 i0 ), является

182

отображением магнитного поля линии в ее схеме замещения, зависит от магнитных характеристик среды (μ) и геометрических размеров линии;

G0 – активная проводимость между проводами на единицу длины ли-

нии [См/м], является следствием несовершенства изоляции между проводами, зависит от электрических параметров среды (γ) и геометрических размеров линии;

C	0

– емкость между проводами на единицу длины линии [Ф/м], опре-

деляется как отношение заряда к напряжению (

C			q
	0		0
			U

), является отобра-

жением электрического поля линии в ее схеме замещения, зависит от электрических характеристик среды ( ) и геометрических размеров линии.

Удельные параметры линии

R	, L	, G	, C	0
0	0	0

зависят от физических па-

раметров самих проводов и окружающей их среды, поэтому они получили название физических или первичных.

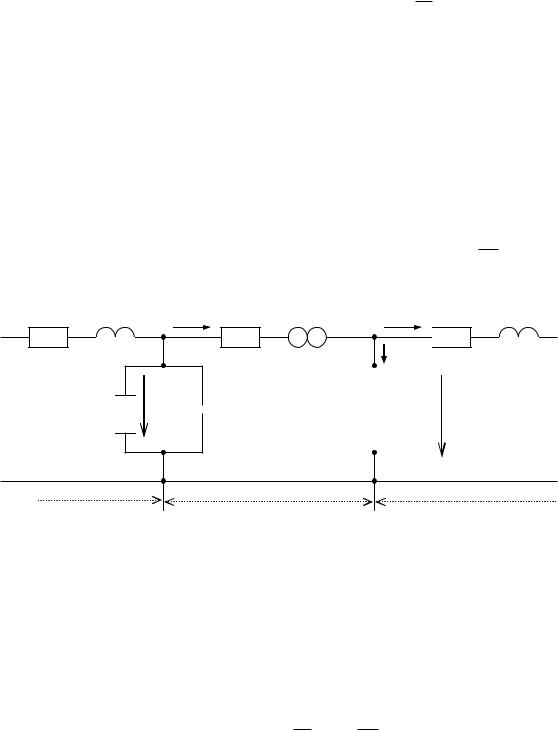
Разделим всю линию на элементарные участки длиной dх и рассмотрим один из таких участков, находящийся на расстоянии х от начала линии. Схема замещения участка будет иметь вид рис. 154. Здесь u и i – напряжение и ток в начале рассматриваемого участка. В конце участка

напряжение и ток получают приращения:

	u	u	dx
		x

и

i

ix

dx

.

i R0dx

G0dx u C0dx

L0dx			i+ ( i / x
			di
G0dx			C0dx

)dx

u+ ( u / x)dx

x	dx		dx

Рис. 154

Функции напряжения и тока (u, i) зависят от двух параметров t и x, они изменяются в пространстве и во времени, поэтому дифференциальные уравнения для схемы замещения следует составлять в частных производных.

Уравнение по 2-му закону Кирхгофа для контура:

u R0 dx i L0 dx ti u ux dx 0 .

183

После упрощения получим:

	u	R i L		i	.
	x	0	0	t

По закону Ома и 1-му закону Кирхгофа:

(1)

di (u

u

dx)G

dx C

dx

(u

u

dx) uG

dx C

dx

u

.

0

0

x

0

t

x

0

t

В приведенном выражении пренебрегаем слагаемыми второго поряд-

ка малости, содержащими

d

2

x

.

По 1-му закону Кирхгофа для узла:

i i

i

dx

di i

i

dx uG dx C

dx

u

0

.

x

x

0

t

После упрощения получим:

		i
		x

G	u C	0
0

ut

.

(2)

Уравнения (1) и (2) являются основными дифференциальными уравнениями двухпроводной линии с распределенными параметрами, которые используются для расчета как переходного, так и установившегося режима линии.

3.Решение уравнений линии с распределенными параметрами

вустановившемся синусоидальном режиме

Пусть напряжение и ток в линии с распределенными параметрами изменяются по синусоидальному закону:

u(t) Um sin( t u) U Ue j u ,

i(t) Im sin( t i) I

Ie

j i

.

Заменим

в

дифференциальных уравнениях линии синусоидальные

функции u(t)

и

i(t) и их производные

u

и

i

соответствующими ком-

t

t

плексными изображениями u(t) U ,

i(t) I ,

u

j

U

,

i j I :

t

t

184

		dU
		dx
		d I
		dx

В уравнениях (1) и

R	I j L	I (R	j L	)I Z	0	I
0	0	0	0

G U j C U (G			j C	)U Y		0	U
0	0	0	0
(2) приняты обозначения:					Z	0		R	j L
								0	0

(1)

(2)

ком-

плексное сопротивление линии на единицу длины [Ом/м],	Y	G	j C	0
	0	0

комплексная проводимость линии на единицу длины [См /м]. Дифференцируем уравнение (2) по переменной х и делаем в него под-

становку из (1):

			d	2	U							d I
								Z							Z						( Y				U ) Z						Y			U
			dx			2				0		dx							0					0						0			0
или
										d		2	U
															Z					Y			U 0																	(3)
										dx				2				0				0
Решаем дифференциальное уравнение 2-го порядка (3) классическим
методом. Характеристическое уравнение и его корни:																																		k	2	Z		Y		0,
																																					0		0
k			Z	0	Y		0							,	k	2					+			Z		0	Y	0		+				.
откуда 1

Решение для искомой функции в общем виде:

где

Z	0	Y	0

	U
(R
0

( x) A e x
	1
j L )(G		j C
0	0	0

A e	x
2
)

,

j

безразмерная ком-

плексная величина, названная коэффициентом (постоянной) распростране-

ния,	A	, A	комплексные постоянные интегрирования, которые опреде-
	1	2

ляются через граничные условия, т. е. через значения искомых функций U(x), I(x) в заданной точке линии, например в ее начале (х = 0) или в ее конце (x = l).

Из уравнения (1) находим:

	I (x)						1		d I			1	( A e- x A			e x )
							Z 0 dx					Z 0		1	2
		Z 0				( A e- x				A		e x )		1	( A e- x A			e	x )	,
											2						2
	1													Z c	1
		Z 0	Y	0

185

					1				Z	0		R		j L							j c
где	Z	c											0			0		Z	C	e		– волновое или характери-
				Z		Y			Y			G		j C
					0		0			0			0				0
стическое сопротивление линии.
	Таким образом, решения для искомых функций U(x) и I(x) имеют вид:
											U ( x) A e- x								A e x						,		(4)
																1						2
											I ( x)				1		( A e- x A							e x )		.	(5)
																							2
															Z			1
															C

Волновое сопротивление

Z C

и постоянная распространения

полу-

чили название вторичных параметров линии.

Выразим постоянные

интегрирования

A1

и

A2

условия начала линии. При

х = 0

U (x) U

1

,

I ( x)

значения в уравнения (4) и (5):

U

1

A A

2

1

I

1

( A

A

)

1

Z C

1

2

через граничные

I	, подставим эти
1

Совместное решение этих уравнений позволяет определить постоян-

ные интегрирования:

A1

1	(U
2	1

I	1	Z	C	)

,

A	2

1	(U
2	1

I	1	Z	C

)

.

Подставим полученные значения постоянных интегрирования в решения для искомых функций (4) и (5):

U ( x)

1

(U

I

Z

)e x

1

(U

I

Z

)e x

1

1

C

1

1

C

2

2

e

x

e

x

e

x

e

x

U

I

Z

) U ch x I

Z

sh x

,

1

1

C

1

C

2

2

1

I ( x)

1

1

I 1 Z C )e

- x

1

1 I

x

(

U

1

(

U

1 Z C )e

Z C

2

2

U

e

x

e

x

e

x

e

x

U

1

I

I

ch x

1

sh x

1

Z

2

2

1

Z

C

C

.

Полученные уравнения используются при расчетах цепей с распределенными параметрами в установившемся синусоидальном режиме.

Если принять х = l ,то получим значения параметров режима в конце линии:

186

				U ch I					sh
U			2			1	Z	C
				1
				I ch	U		sh
	I				1
		2		1	Z C

.

Выразим постоянные интегрирования через граничные условия конца линии. Для этой цели в полученных ранее решениях (4) и (5) заменим переменные х на l – y из условия x = l y, где l – длина всей линии, а y – расстояние от конца линии до рассматриваемой точки:

Здесь

U

A3

( y) A e					( y)		A		e ( y) A e									e y A		e e y
			1					2						1					2
A e e y							A e e y							A e y A e y
	1							2									3			4	,
		I ( y)				1		( A e ( y )						A				e ( y ) )
																	2
						Z			1
							c
	1		( A e e y A e e y )											1		( A e y A e y )
																					.
	Z				1				2					Z				3	4
		c													c
A e		l		,	A		A			e	l		есть некоторые новые постоянные
	1					3			2

интегрирования.

При y = 0	U ( y) U

ные уравнения, получим:

2

,

I ( y) I 2

подставим эти значения в найден-

U			2	A		3	A		4
	I				1		( A		A	)
		2						3
					Z C				4

Совместное решение этих уравнений позволяет определить постоянные интегрирования:

A3

1	(U
2	2

I	2	Z	C	)

,

A4 12 (U 2 I 2 Z c )

Подставляем значения постоянных в решение для искомых функций:

U ( y)

1

(U

I

Z

)e y

1

(U

I

Z

)e y

2

2

C

2

2

C

2

2

U

e y e y

I 2 Z C

e y e y

U

2 ch y I 2 Z C sh y ,

2

2

2

I ( y)

1

1

(U

I

Z

)e

y

1

(U

I

Z

)e

y

2

2

C

2

2

C

Z

2

2

C

I 2

e y e y

U

2

e y e y

I

2ch y

U

2

sh y .

Z C

2

2

Z C

187

Полученные уравнения используются при расчете цепей с распределенными параметрами в установившемся синусоидальном режиме.

Если принять y = l, то получим значение параметров режима в начале линии:

		U	1		U	2ch l I 2 Z C sh l
				I 2ch l			U		2	sh l
	I 1
							Z C

4. Волновые процессы в линии с распределенными параметрами

Ранее были получены решения для напряжения и тока в установившемся режиме:

		U (x) A e- x A														e x				,
						1								2
	I (x)						1	( A e- x A e x )														.
							Z c		1						2
Учитывая, что постоянные интегрирования и коэффициент
странения являются комплексными числами (																	A			a e			j	,		A
																							1				2
																			1			1
j
) преобразуем уравнение для U(x):
U ( x) a e				j		( j ) x					a			e	j			2 e			( j ) x
					1 e								2
	1
a e	x	e		j( x					)	a				e	x				e			j( x		2	)
						1						2														.
1

распро-

a		e	j	2	,
	2

Перейдем от комплексного изображения функции к ее оригиналу, т.е. к ее функции времени:

u(x,t)	2a e x sin( t x )		2a	e x sin( t x	2	)
	1	1	2

U1m (x) sin( t x 1) U2m (x) sin( t x 2 ) un (x,t) uo (x,t) .

Функция u(x,t) состоит из двух слагаемых, первое из которых представляет собой прямую или падающую волну uп(x,t), а второе обратную или отраженную волну uо(x,t). Проанализируем, как изменяется каждая из волн в пространстве и во времени.

Падающая волна напряжения равна:

un ( x, t) 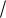2a1e x sin( t x 1 ) .

188

В произвольной точке линии	x x
	/

по синусоидальному закону с постоянной

const напряжение изменяется амплитудой:

где

U m

u	n	( x , t)
	2a e		- x
		1

2

a e	x	'
1
const
	,

sin( t

x	) U
1	m

	x	.
1

sin( t

)

,

В произвольно выбранный момент времени	t t		const	напряже-

ние вдоль линии изменяется по синусоидальному закону, но с затуханием амплитуды с увеличением расстояния х:

u

n

( x, t )

2a e- x sin( t x ) U

m

( x) sin( x )

,

1

где

U

( x)

2a e

- x

,

.

m

1

Коэффициент β

показывает, как изменяется фаза падающей волны

напряжения на единицу длины линии [рад/м] и называется коэффициентом фазы.

Длиной волны λ называется расстояние ∆х между двумя ближайшими точками линии, которые находятся в одинаковом фазовом состоянии, т.е. через интервал 2π:

β∆x = βλ = 2π, откуда следует

2

.

С течением времени синусоидальное распределение напряжения перемещается вдоль линии. Под скоростью распространения волны или фазовой скоростью понимают скорость перемещения вдоль линии определенного фазового состояния, для чего должно удовлетворяться условие:

t x

1

const

.

Продифференцируем члены этого уравнения, в результате полу-

чим: dt dx 0

, откуда следует:

dx

2 f

f

n

dt

2 /

Неравенство

n > 0 означает, что падающая волна перемещается в

положительном в направлении, т. е. от начала линии к ее концу.

Амплитуда

падающей

волны

зависит

от координаты х:

- x

- x

U m ( x) 2a1e

, она убывает (затухает) по показательному закону

e

в направление возрастания х, т.е. в направлении движения волны. Скорость затухания определяется коэффициентом α, который получил название коэффициента затухания волны [Неп/м].

Коэффициент	j	показывает в комплексе характер измене-

ния волны при движении ее вдоль линии, поэтому получил название коэффициента распространения волны.

Характер распространения падающей волны напряжения un ( x, t ) показан на рис. 179.

189

u

un(t )

un(t + t)

v

x

Рис. 155

Отраженная волна напряжения равна:

u	( x, t)
o

Фазовая скорость

	2a		e	x	sin( t
		2

отраженной волны

x	2	)	,

найдется из уравнения:

t x	2	const.

После дифференцирования получим:

dt dx 0

0

, откуда следует

				dx
		0		dt				n

Отраженная волна распространяется с той же фазовой скоростью, что и падающая, но в обратном направлении (знак минус), т.е. от конца линии

к ее началу. Она имеет ту же длину волны 2 . Амплитуда отражен-

ной волны

U	mo	( x)

2a		e	x
	2

, при α > 0 убывает (затухает) в направлении

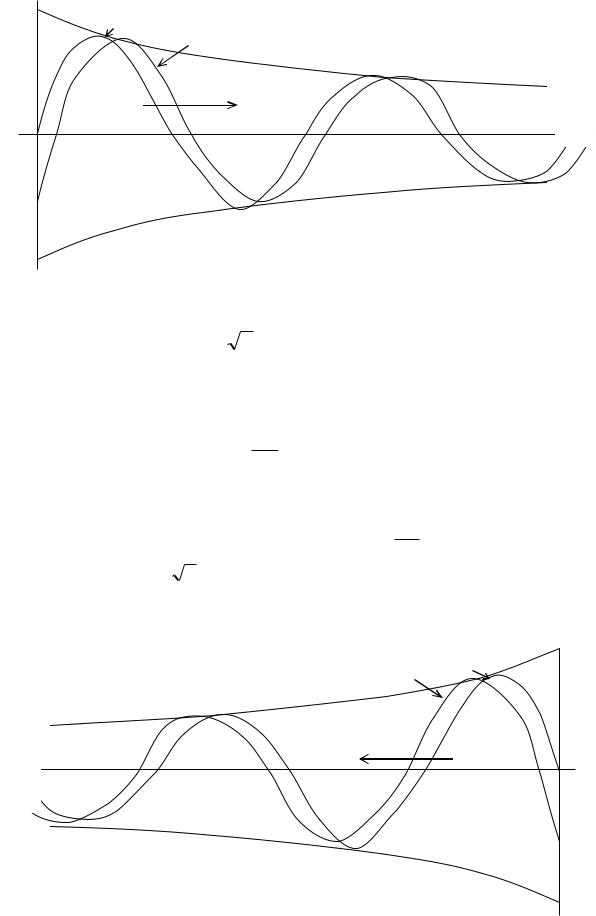
уменьшения координаты х , т.е. в направлении движения волны. Характер распространения отраженной волны показан на рис. 156.

un(t + t)	uo(t )	u
v

y

Рис. 156

190