
Ряды в комплексной плоскости
.doc§8 Числовые ряды
Ряд
![]() ,
(23)
,
(23)
членами которого являются комплексные числа, называется числовым рядом (в комплексной области). Ряд (23) можно записать в виде
![]()
где
![]() и
и
![]()
![]()
действительные числа.
действительные числа.
Сумма
![]() первых
первых
![]() членов ряда (23) называется
членов ряда (23) называется
![]() частичной
суммой ряда.
частичной
суммой ряда.
Если
существует конечный предел
![]() последовательности частичных сумм
последовательности частичных сумм
![]() ряда:
ряда:
![]() то ряд (23) называется сходящимся, а
то ряд (23) называется сходящимся, а
![]() суммой ряда; если
суммой ряда; если
![]() не существует, то ряд (23) называется
расходящимся.
не существует, то ряд (23) называется
расходящимся.
Очевидно, что ряд (23) сходится тогда и только тогда, когда сходится каждый из рядов
![]() (24)
(24)
![]() (25)
(25)
При
этом
![]() где
где
![]() сумма ряда(24), а
сумма ряда(24), а
![]() сумма ряда (25). Это означает, что
исследование сходимости ряда с
комплексными членами сводится к
исследованию сходимости рядов (24), (25) с
действительными членами.
сумма ряда (25). Это означает, что
исследование сходимости ряда с
комплексными членами сводится к
исследованию сходимости рядов (24), (25) с
действительными членами.
В теории рядов с комплексными членами основные определения, многие теоремы и их доказательства аналогичны соответствующим определениям и теоремам из теории рядов с действительными членами.
Приведем некоторые из них.
Теорема:
(необходимый
признак сходимости ряда). Если ряд (23)
сходится, то его общий член
![]() при
при
![]() стремится к нулю, т.е.
стремится к нулю, т.е.
![]()
Ряд (23) называется абсолютно сходящимся, если сходится ряд
![]() (26)
(26)
Теорема: Если сходится ряд (26), то абсолютно сходится ряд (23).
При
исследовании на сходимость рядов с
комплексными членами применимы все
известные из действительного анализа
признаки сходимости знакопостоянных
рядов, в частности признак
Даламбера:
Если существует
![]() ,
то при
,
то при
![]() ряд (26) абсолютно сходится, а при
ряд (26) абсолютно сходится, а при
![]()
расходится.
расходится.
§9 Степенные ряды
Степенным рядом в комплексной области называется ряд
![]() ,
(27)
,
(27)
или
ряд
![]() ,
(28)
,
(28)
где
![]() комплексные числа (коэффициенты ряда),
комплексные числа (коэффициенты ряда),
![]()
Ряды
(27) и (28) при одних значениях аргумента
![]() могут
сходиться, при других
расходиться. Совокупность всех значений
могут
сходиться, при других
расходиться. Совокупность всех значений
![]() ,
при которых ряд (27) [(28)] сходится, называется
областью
сходимости
этого ряда.
,
при которых ряд (27) [(28)] сходится, называется
областью
сходимости
этого ряда.
Теорема
(Абеля):
Если степенной ряд (27) сходится при
![]() (в точке
(в точке
![]() ,
то он абсолютно сходится при всех
значениях
,
то он абсолютно сходится при всех
значениях
![]() ,
удовлетворяющих условию
,
удовлетворяющих условию
![]()
Следствие:
Если ряд (27) расходится при
![]() ,
то он расходится при всех значениях
,
то он расходится при всех значениях
![]() ,
удовлетворяющих условию
,
удовлетворяющих условию
![]() ,
т.е. вне круга радиуса
,
т.е. вне круга радиуса
![]() с центром в начале координат.
с центром в начале координат.
Из
теоремы Абеля следует, что существует
такое число
![]() ,
что при всех
,
что при всех
![]() ,
для которых
,
для которых
![]() ,
степенной ряд (27) абсолютно сходится.
Эти точки лежат на комплексной плоскости
внутри круга радиуса
,
степенной ряд (27) абсолютно сходится.
Эти точки лежат на комплексной плоскости
внутри круга радиуса
![]() с центром в точке
с центром в точке
![]()
Величина
![]() называется радиусом сходимости ряда,
круг
называется радиусом сходимости ряда,
круг
![]() называется кругом сходимости ряда, вне
этого круга ряд расходится, а на границе
может как сходиться, так и расходиться.
называется кругом сходимости ряда, вне
этого круга ряд расходится, а на границе
может как сходиться, так и расходиться.
Если
![]() ,
то ряд (27) сходится в точке
,
то ряд (27) сходится в точке
![]() ,
если
,
если
![]() ,
то ряд сходится на всей комплексной
плоскости. Для ряда (28) кругом сходимости
является круг
,
то ряд сходится на всей комплексной
плоскости. Для ряда (28) кругом сходимости
является круг
![]() с центром в точке
с центром в точке
![]() .
.
Радиус сходимости находится по формулам:
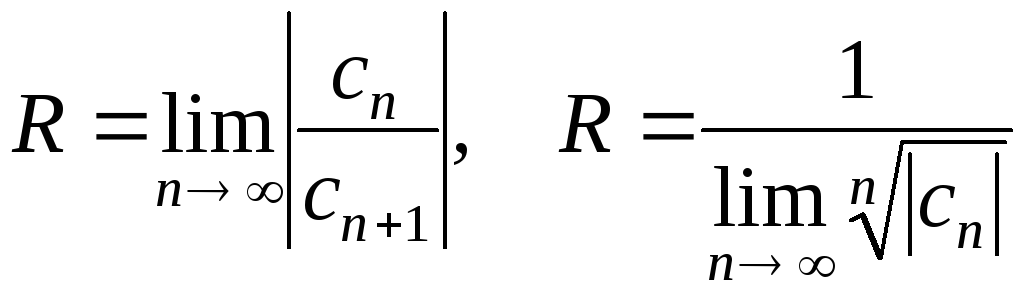 .
.
Свойства ряда (27), (28):
-
Сумма степенного ряда внутри круга его сходимости есть аналитическая функция;
-
Степенной ряд внутри круга сходимости можно почленно дифференцировать и почленно интегрировать любое число раз, полученный при этом ряд имеет тот же радиус сходимости, что и исходный ряд.
Примеры: Найти область сходимости рядов:
Решение:
Здесь
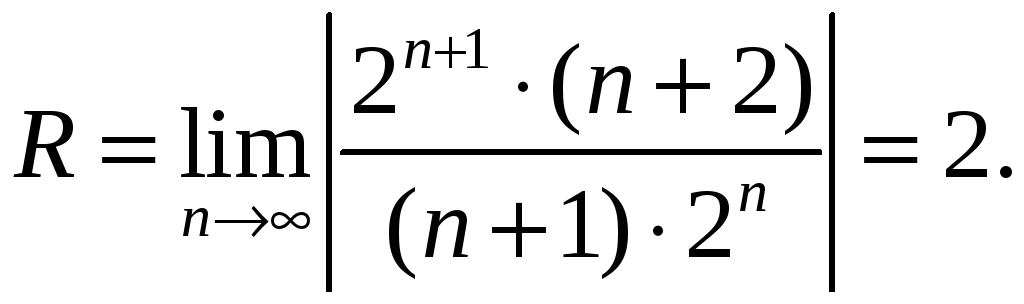 Данный ряд сходится в области
Данный ряд сходится в области
![]()
-
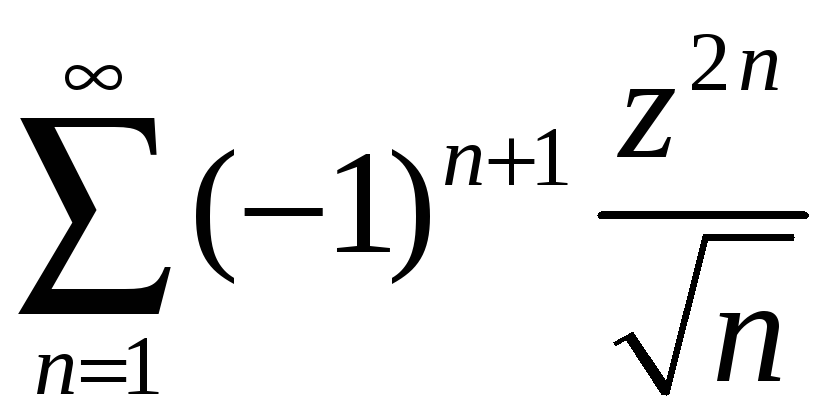 и
исследовать сходимость ряда в точках
и
исследовать сходимость ряда в точках
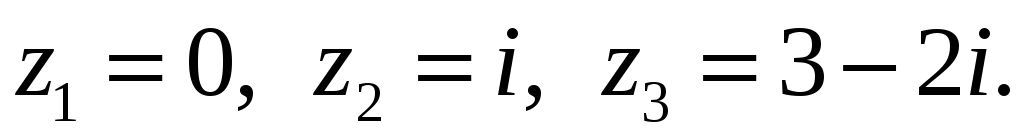
Решение: Здесь
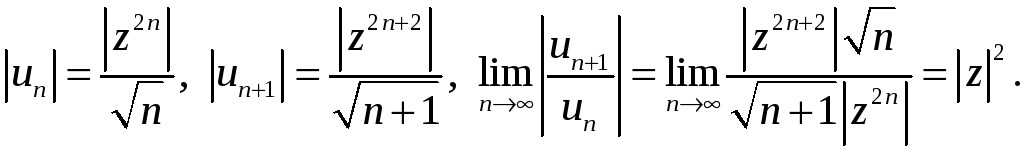 Ряд
сходится при всех
Ряд
сходится при всех
![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
![]() т.
е.
т.
е.
![]() Кругом сходимости является круг с
центром в точке
Кругом сходимости является круг с
центром в точке
![]() и радиусом равным 1.
и радиусом равным 1.
Точка
![]() лежит внутри круга сходимости, в этой
точке ряд сходится абсолютно. Точка
лежит внутри круга сходимости, в этой
точке ряд сходится абсолютно. Точка
![]() лежит на границе круга сходимости, в
этой точке ряд может сходится (абсолютно
или условно) и расходиться. Подставляя
значение
лежит на границе круга сходимости, в
этой точке ряд может сходится (абсолютно
или условно) и расходиться. Подставляя
значение
![]() в выражение общего члена ряда, получим
в выражение общего члена ряда, получим
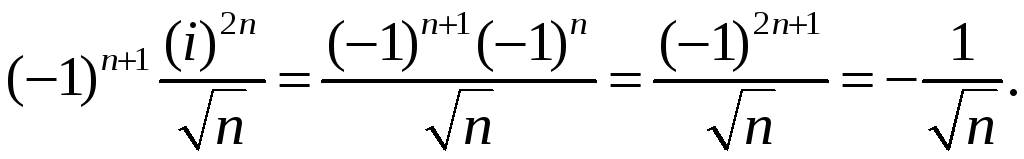 Числовой ряд с общим членом
Числовой ряд с общим членом
 расходится согласно интегральному
признаку Коши. Следовательно, в точке
расходится согласно интегральному
признаку Коши. Следовательно, в точке
![]() степенной ряд
степенной ряд
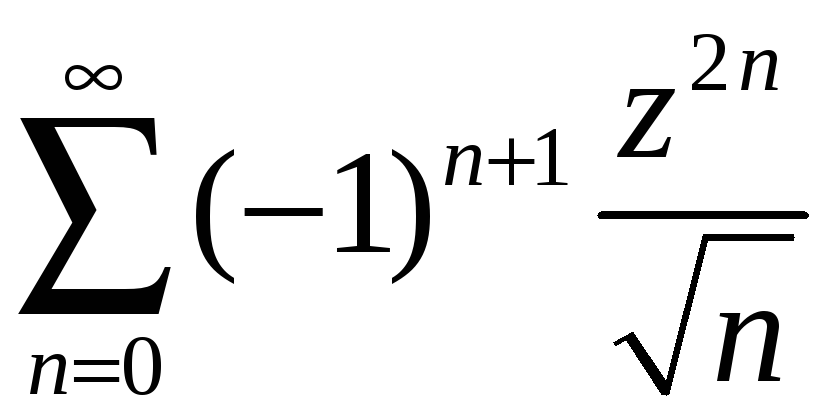 расходится.
расходится.
Точка
![]() лежит вне круга сходимости, ряд в этой
точке расходится.
лежит вне круга сходимости, ряд в этой
точке расходится.
§10 Ряд Тейлора
Теорема:
Всякая аналитическая в круге
![]() функция
функция
![]() может быть единственным образом разложена
в этом круге в степенной ряд
может быть единственным образом разложена
в этом круге в степенной ряд
![]() ,
(29)
,
(29)
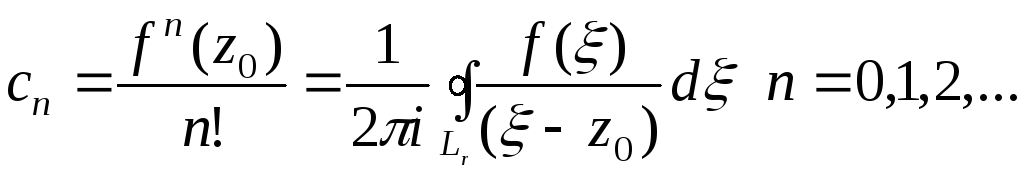 ,
(30)
,
(30)
где
![]()
произвольная окружность с центром в
точке
произвольная окружность с центром в
точке
![]() ,
лежащая внутри круга.
,
лежащая внутри круга.
Степенной
ряд (29) называется рядом Тейлора для
функции
![]() в рассматриваемом круге.
в рассматриваемом круге.
Приведем разложение некоторых элементарных функций в ряд Тейлора (Маклорена):
![]()
![]()
![]()
![]()
![]()
Первые
три разложения справедливы во всех
точках комплексной плоскости, последние
два – в круге
![]()
Заменив
![]() на
на
![]() в разложении функции
в разложении функции
![]() ,
получим:
,
получим:
![]() т.е.
формулу Эйлера
т.е.
формулу Эйлера
![]()

