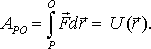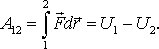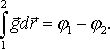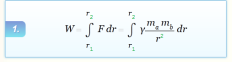Часть 1.

1) Системы отсчета. Уравнения движения. Скорость, ускорение.

Система отсчёта — это совокупность тела отсчета, связанной с ним системы координати системы отсчётавремени, по отношению к которым рассматривается движение (или равновесие) каких-либоматериальных точекили тел.

Инерциа́льная систе́ма отсчёта (ИСО) — система отсчёта, в которой справедлив первый закон Ньютона (закон инерции): все свободные тела (то есть такие, на которые не действуют внешние силы или действие этих сил компенсируется) движутся прямолинейно и равномерно или покоятся.

Инерциальной называется система отсчёта, по отношению к которой пространствоявляетсяоднороднымиизотропным, авремя—однородным.

Свойства инерциальных систем отсчёта

Всякая система отсчёта, движущаяся относительно ИСО равномерно и прямолинейно, также является ИСО. Согласно принципу относительности, все ИСО равноправны, и всезаконы физикиинвариантны относительно перехода из одной ИСО в другую. Это значит, что проявления законов физики в них выглядят одинаково, и записи этих законов имеют одинаковую форму в разных ИСО.

Предположение о существовании хотя бы одной ИСО в изотропномпространстве приводит к выводу о существовании бесконечного множества таких систем, движущихся друг относительно друга со всевозможными постоянными скоростями. Если ИСО существуют, то пространство будет однородным и изотропным, а время — однородным; согласнотеореме Нётер, однородность пространства относительно сдвигов даст закон сохраненияимпульса, изотропность приведёт к сохранениюмомента импульса, а однородность времени — к сохранениюэнергиидвижущегося тела.

В специальной теории относительностискорости относительного движения ИСО, реализуемых действительными телами, не могут превышать некоторойконечной скорости«C» (скорость распространения света в вакууме) и связь между координатами и моментами времени любого «события» в разных ИСО осуществляется преобразованиями Лоренца.

Неинерциа́льная систе́ма отсчёта — система отсчёта, к которой не применим законинерции(говорящий о том, что каждое тело, в отсутствие действующих на него сил, движется по прямой и с постоянной скоростью), и поэтому для согласования сил и ускорений в которой приходится вводить фиктивныесилы инерции. Всякая система отсчета, движущаяся с ускорением относительно инерциальной, является неинерциальной.

Законы Ньютонавыполняются только в инерциальных системах отсчёта. Для того, чтобы найти уравнение движения в неинерциальной системе отсчёта, нужно знать законы преобразования сил и ускорений при переходе от инерциальной системы к любой неинерциальной.

равноускоренное, равнозамедленное (равнопеременное), равномерное.

Уравнения движения , Скорость ,ускорение. (в тетрадке, подготовка ко второй лабороторной работе)

2) Ускорение. Тангенциальное и нормальное ускорение.

Тангенциальное и нормальное ускорение

Вектор a - ускорение материальной точки - характеризует быстроту изменения ее скорости v как по модулю, так и по направлению.

Поэтому часто вместо выражения вектора ускорения через три его проекции на оси координат удобнее представлять его в виде геометрической суммы только двух составляющих, направленных по касательной и нормали к траектории. При этом составляющая, направленная по касательной к траектории и называемая тангенциальным (касательным) ускорением, будет характеризовать быстроту изменения величины скорости.

Составляющая же, направленная по нормали к траектории и называемая нормальным (или центростремительным) ускорением, будет характеризовать быстроту изменения скорости только по направлению. Найдем эти составляющие ускорения.

С этой целью удобнее всего использовать так называемый "естественный" способ описания движения точки, который применяют тогда, когда заранее известна траектория точки.

Движение точки определено, если известны ее траектория, начало отсчета O, положительное направление дуговой координаты l и закон движения точки, то есть зависимость l(t).

Рассмотрим движение материальной точки (рис. 14).

В момент времени t0 ее скорость – 0, в момент времени t скорость>0. Траектория – кривая линия.

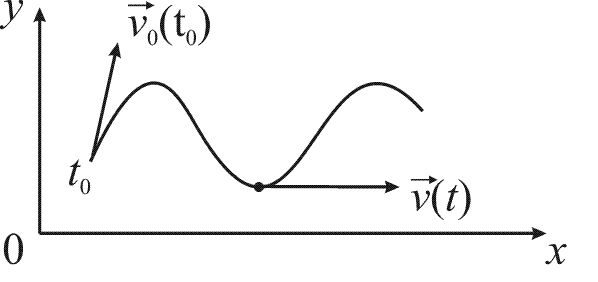
Рис. 14

За интервал времени t = t – t0 скорость изменяется и по направлению, и по модулю (числовому значению).

Построим вектор изменения скорости (рис. 15):

.

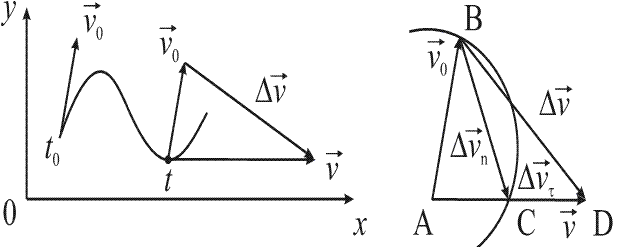
Рис. 15

Разложим вектор на два вектораи.

Для этого по линии вектора отложим отрезок |AC|, длина которого равна |0|:

.

Соединим точки В и С. Построим вектор . Вектор. Из рис. 16 видно, что– результирующий вектор:

. (10)

Вектор характеризует изменение скорости за интервал времениt по направлению.

Вектор характеризует изменение скорости за интервал времениt по модулю (числовому значению).

Разделим две части уравнения (10) на t0:

.

При t0 имеем:

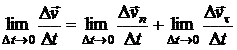. (11)

По определению (формула (7)):

(полное ускорение).

Физическая величина, характеризующая изменение скорости по направлению, – нормальное ускорение.

.

Физическая величина, характеризующая изменение скорости по модулю, – тангенциальное ускорение.

.

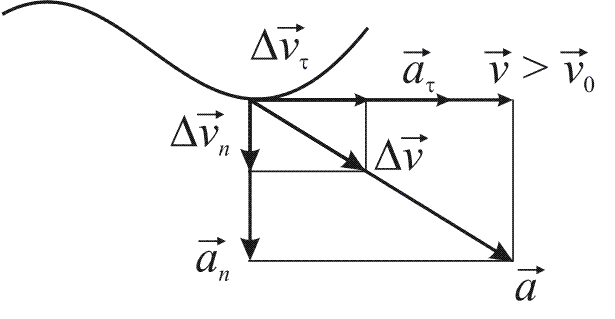
Тогда из уравнения (11) следует, что вектор полного ускорения равен векторной сумме тангенциального и нормального ускорений:

. (12)

Мы знаем, что направления векторов ускорения и изменения скорости всегда совпадают: . На рис. 16 векторсовпадает с. Разложим вектор ускоренияна две взаимно перпендикулярные компоненты – тангенциальнуюt, совпадающую с вектором скорости, и перпендикулярнуюn к вектору. Модуль полного ускорения равен:

. (13)

3) Уравнения пути равномерного и равноускоренного движения.

равноускоренное, равнозамедленное (равнопеременное), равномерное.

Вывод формул, формулы, пояснения, описания.

4) Кинематика криволинейного движения. Вращение, линейная и угловая скорости, частота вращения, угловое ускорение.

Движение по окружности и его кинематические характеристики. 

 Описание движения по окружности. Для начала рассмотрим один из простых случаев криволинейного движения частицы - движение, при котором меняется только направление ее радиуса-вектора r(t). Уравнение, характеризующее изменение положения частицы со временем, будет иметь вид:

r(t) = r·e_r(t), где r = const.

 

Пусть радиус-вектор частицы описывает круговой конус. Тогда его сечение плоскостью перпендикулярной оси OZ образует окружность радиуса r (см. рис. 2.1). В декартовой системе координат уравнения движения примут вид:

x(t) = r·cos f(t);  y(t) = r·sin f(t).

Траектория будет описываться следующим уравнением:

x² + y² = r².

В случае равномерного движения по окружности угол изменяется со временем по закону f(t) = w·t + f₀, а мировая линия в трехмерном мире событий будет представлять из себя винтовую линию, которая симметрична относительно оси Ot и имеет шаг, равный периоду T = 2p/w.

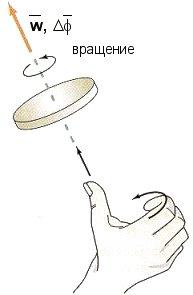  Рис. 2.2. К определению направления векторов элементарного углового перемещения и угловой скорости. 

Вектор угловой скорости и ускорения. То, что величина элементарного углового перемещения является вектором, можно доказать, выразив ее как комбинацию других известных нам векторных величин. Докажем это на примере вектора угловой скорости w, который параллелен df. 

Используя определение угловой скорости, как производной от угла по времени:

w = df/dt,

выразим ее через другие известные нам векторные величины. Модуль вектора скорости равен:

 

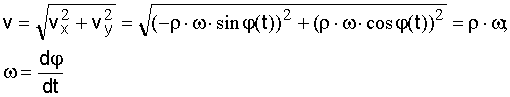
С учетом направлений векторов скалярное равенство v = w·r можно записать в векторном виде:

v = [w·r].

Аналогично можно получить уравнение для нахождения угловой скорости, как комбинации векторов v и r:

w = [r·v]/r².

Вектор углового ускорения  вводится по аналогии с поступательным движением, т.е. как производная от угловой скорости по времени:

e = dw/dt.

Вектор углового ускорения при неизменной ориентации ее оси вращения направлен вдоль этой оси (параллельно или антипараллельно вектору w). 

Если а.т.т. участвует одновременно в нескольких вращательных движениях, то его угловая скорость равна векторной сумме угловых скоростей каждого из движений: w = w₁+ w₂+ ... + w_n.

Прецессия. Движение любого вектора, конец которого перемещается по окружности, описывая со временем конус вокруг некоторой оси, не совпадающей с направлением вектора угловой скорости называется прецессией. Вектор скорости для прецессионного движения равен:

v = dr/dt = [w·r] = {- df/dt·r_y, df/dt·r_x, 0}.

Прецессия характерна не только для механических объектов. Она, например, присуща электронам в атомах, помещенным в магнитное поле.

Угловая скорость и угловое ускорение

Рассмотрим твердое тело, которое вращается вокруг неподвижной оси. Тогда отдель­ные точки этого тела будут описывать окружности разных радиусов, центры которых лежат на оси вращения. Пусть некоторая точка движется по окружности радиуса R (рис. 6). Ее положение через промежуток времени Dt зададим углом D. Элементар­ные (бесконечно малые) повороты можно рассматривать как векторы (они обозначают­ся  или ). Модуль вектора равен углу поворота, а его направление совпадает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, т.е. подчиняется правилу правого винта (рис.6). Векторы, направления которых связываются с направлением вращения, назы­ваются псевдовекторами или аксиальными векторами. Эти векторы не имеют опреде­ленных точек приложения: они могут откладываться из любой точки оси вращения.

Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

Вектор  направлен вдоль оси вращения по правилу правого винта. Размерность угловой скорости dim w=T^–1, а ее единица — ради­ан в секунду (рад/с).

Линейная скорость точки

т. е.

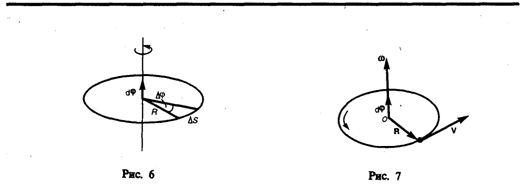
В векторном виде формулу для линейной скорости можно написать как векторное произведение:

При этом модуль векторного произведения, по определению, равен , а направление совпадает с направлением поступательного движения правого винта при его вращении откR.

Если (=const, то вращение равномерное и его можно характеризовать периодом вращения T — временем, за которое точка совершает один полный оборот, т.е. поворачивается на угол 2p. Так как промежутку времени Dt = T соответствует = 2p, то = 2p/T, откуда

Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения:

откуда

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости.

При ускоренном движении вектор сонаправлен вектору(рис.8), при замедлен­ном — противонаправлен ему (рис.9).

Тангенциальная составляющая ускорения

Нормальная составляющая ускорения

Таким образом, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение , нормальное ускорение) и угловыми величинами (угол поворота j, угловая скорость w, угловое ускорение e) выражается следующими формулами:

В случае равнопеременного движения точки по окружности (e=const)

      

где  w₀ — начальная угловая скорость.

5) Динамика. Законы Ньютона. Инерциальные системы. Границы применимости законов Ньютона.

Законы Ньютона.

Классическая динамика основана на трёх основных законах Ньютона:

1-й: Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или их действие скомпенсировано.

2-й: В инерциальной системе отсчета сумма всех сил, действующих на тело, равна произведению массы этого тела на векторное ускорение этого же тела (действие на тело силы, проявляется в сообщении ему ускорения).

В наиболее общем случае, который описывает также движение тела с изменяющейся массой (например, реактивное движение), 2-й закон Ньютона принято записывать следующим образом:

,

где —импульс тела. Таким образом, сила характеризует быстроту изменения импульса.

3-й: Тела действуют друг на друга силами равными по модулю и противоположными по направлению

Если при этом рассматриваются взаимодействующие материальные точки, то обе эти силы действуют вдоль прямой, их соединяющей. Это приводит к тому, что суммарный момент импульса системы состоящей из двух материальных точек в процессе взаимодействия остается неизменным. Таким образом, из второго и третьего законов Ньютона могут быть получены законы сохранения импульса и момента импульса

Законы Ньютона в неинерциальных системах отсчета

Существование инерциальных систем отсчета лишь постулируется первым законом Ньютона. Реальные системы отсчета, связанные, например, с Землей или с Солнцем, не обладают в полной мере свойством инерциальности в силу их кругового движения. Вообще говоря, экспериментально доказать существование ИСО невозможно, поскольку для этого необходимо наличие свободного тела (тела на которое не действуют никакие силы), а то, что тело является свободным, может быть показано лишь в ИСО. Описание же движения в неинерциальных системах отсчета, движущихся с ускорением относительно инерциальных, требует введения т. н. фиктивных сил таких как сила инерции, центробежная сила или сила Кориолиса. Эти «силы» не обусловлены взаимодействием тел, то есть по своей природе не являются силами и вводятся лишь для сохранения формы второго закона Ньютона:

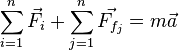
где — сумма всех фиктивных сил, возникающих в неинерциальной системе отсчета.

Описание динамики исходя из принципа наименьшего действия

Многие законы динамики могут быть описаны исходя не из законов Ньютона, а из принципа наименьшего действия.

Формулы некоторых сил, действующих на тело

Сила всемирного тяготения:

или в векторной форме:

вблизи земной поверхности:

Сила трения:

Сила Архимеда:

Границы применимости механики Ньютона. До конца прошлого столетия никто не сомневался в абсолютной правильности законов Ньютона. Однако в XX в. выяснилось, что эти законы все-таки не абсолютно точны.

Ими нельзя пользоваться, когда тела движутся с очень большими скоростями, которые сравнимы со скоростью света. Альберт Эйнштейн, которого называют Ньютоном XX в., сумел сформулировать законы движения, справедливые и для движения со скоростями, близкими к скорости света.

Эти законы лежат в основе так называемой релятивистской механики или теории относительности. А законы Ньютона представляют собой следствие этих законов, когда скорости тел малы по сравнению со скоростью света.

Законы Ньютона нельзя применять и при рассмотрении движения внутриатомных частиц. Такие движения описываются законами квантовой механики, в которой классическая механика рассматривается как частный случай.

Законы сохранения импульса и энергии, выведенные из законов Ньютона, справедливы и в квантовой механике, и в теории относительности. Механика лежит в основе всего естествознания.

6) Механический принцип относительности. Преобразования Галилея.

Преобразования Галилея и механический принцип относительности.

В классической механике справедлив механический принцип относительности (принцип относительности Галилея): законы динамики одинаковы во всех инерциальных систе­мах отсчета.

Для его доказательства рассмотрим две системы отсчета: инерциальную систему K (с координатами х, у, z), которую условно будем считать неподвижной, и систему K' (с координатами x', у', z'), движущуюся относительно K равномерно и прямолинейно со скоростью u (u=const). Отсчет времени начнем с момента, когда начала координат обеих систем совпадают. Пусть в произвольный момент времени t расположение этих систем друг относительно друга имеет вид, изображенный на рис. 58. Скорость u направлена вдоль OO', радиус-вектор, проведенный из О в О', r₀=ut.

Найдем связь между координатами произвольной точки А в обеих системах. Из рис. 58 видно, что

(34.1)

Уравнение (34.1) можно записать в проекциях на оси координат:

(34.2)

Уравнения (34.1) и (34.2) носят название преобразований координат Галилея.

В частном случае, когда система К' движется со скоростью т вдоль положительного направления оси х системы К (в начальный момент времени оси координат совпадают), преобразования координат Галилея имеют вид

В классической механике предполагается, что ход времени не зависит от относи­тельного движения систем отсчета, т. е. к преобразованиям (34.2) можно добавить еще одно уравнение:

(34.3)

Записанные соотношения справедливы лишь в случае классической механики (u<<с), а при скоростях, сравнимых со скоростью света, преобразования Галилея заменяются более общими преобразованиями Лоренца 

Продифференцировав выражение (34.1) по времени (с учетом (34.3)), получим уравнение

(34.4)

которое представляет собой правило сложения скоростей в классической механике.

Ускорение в системе отсчета К

Таким образом, ускорение точки А в системах отсчета К и К', движущихся друг относительно друга равномерно и прямолинейно, одинаково:

(34.5)

Следовательно, если на точку А другие тела не действуют (а=0), то, согласно (34.5), и а'=0, т. е. система К' является инерциальной (точка движется относительно нее равномерно и прямолинейно или покоится).

Таким образом, из соотношения (34.5) вытекает подтверждение механического принципа относительности: уравнения динамики при переходе от одной инерциальной системы отсчета к другой не изменяются, т. е. являются инвариантными по отношению к преобразованиям координат. Галилей обратил внимание, что никакими механичес­кими опытами, проведенными в данной инерциальной системе отсчета, нельзя устано­вить, покоится ли она или движется равномерно и прямолинейно. Например, сидя в каюте корабля, движущегося равномерно и прямолинейно, мы не можем определить, покоится корабль или движется, не выглянув в окно.

7) Масса, импульс тела. Закон сохранения импульса. Центр масс.

масса есть в тетраде.

Импульс тела- физ. величина равная произведению массы тела на скорость его движения. Импульс- векторная величина, в си измеряется (кг*м/с).

Закон сохранения импульса- в инерциальной системе отсчета суммарный импульс системы тел с течением времени не изменяется.

Центр масс, центр ине́рции — (в механике) геометрическая точка, характеризующая движение тела или системы частиц как целого.

Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом:

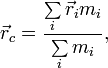
где

—радиус-вектор центра масс,

—радиус-вектор i-й точки системы,

—масса i-й точки.

Для случая непрерывного распределения масс:

где:

—суммарная масса системы,

—объём,

—плотность.

Центр масс, таким образом, характеризует распределение массы по телу или системе частиц.

Понятие центра масс широко используется в физике.

Движение твёрдого тела можно рассматривать как суперпозицию движения центра масс и вращательного движения тела вокруг его центра масс. Центр масс при этом движется так же, как двигалось бы тело с такой же массой, но бесконечно малыми размерами (материальная точка). Последнее означает, в частности, что для описания этого движения применимы все законы Ньютона. Во многих случаях можно вообще не учитывать размеры и форму тела и рассматривать только движение его центра масс.

Часто бывает удобно рассматривать движение замкнутой системы в системе отсчёта, связанной с центром масс. Такая система отсчёта называется системой центра масс (Ц-система), или системой центра инерции. В ней полный импульс замкнутой системы всегда остаётся равным нулю, что позволяет упростить уравнения её движения.

8) Природа сил. Виды сил в механике.

силы в тетраде.

9) Закон всемирного тяготения.

Закон всемирного тяготения.

Подобно тому как Луна движется вокруг Земли, Земля в свою очередь обращается вокруг Солнца. Вокруг Солнца обращаются Меркурий, Венера, Марс, Юпитер и другие планеты Солнечной системы. Ньютон доказал, что движение планет вокруг Солнца происходит под действием силы притяжения, направленной к Солнцу и убывающей обратно пропорционально квадрату расстояния от него. Земля притягивает Луну, а Солнце — Землю, Солнце притягивает Юпитер, а Юпитер — свои спутники и т. д. Отсюда Ньютон сделал вывод, что все тела во Вселенной взаимно притягивают друг друга.

Силу взаимного притяжения, действующую между Солнцем, планетами, кометами, звездами и другими телами во Вселенной, Ньютон назвал силой всемирного тяготения.

Сила всемирного тяготения, действующая на Луну со стороны Земли, пропорциональна массе Луны . Очевидно, что сила всемирного тяготения, действующая со стороны Луны на Землю, пропорциональна массе Земли. Эти силы по третьему закону Ньютона равны между собой. Следовательно, сила всемирного тяготения, действующая между Луной и Землей, пропорциональна массе Земли и массе Луны, т. е. пропорциональна произведению их масс.

Распространив установленные закономерности — зависимость силы тяжести от расстояния и от масс взаимодействующих тел — на взаимодействие всех тел во Вселенной, Ньютон открыл в 1682 г. закон всемирного тяготения: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними:

. (9.3)

Векторы сил всемирного тяготения направлены вдоль прямой, соединяющей тела.

Закон всемирного тяготения в такой форме может быть использован для вычисления сил взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними. Ньютон доказал, что для однородных шарообразных тел закон всемирного тяготения в данной форме применим при любых расстояниях между телами. За расстояние R между телами в этом случае принимается расстояние между центрами шаров.

Силы всемирного тяготения называют гравитационными силами, а коэффициент пропорциональности G в законе всемирного тяготения называют гравитационной постоянной.

Все тела взаимодействуют друг с другом с силой, прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними.

Сила тяжести - это сила притяжения тел к Земле (к планете).

- из закона Всемирного тяготения. (где M - масса планеты, m - масса тела, R - расстояние до центра планеты).

- сила тяжести из второго закона Ньютона (где m - масса тела, g - ускорение силы тяжести).

- ускорение силы тяжести не зависит от массы тела (опыты Галилея).

g₀»9,81 м/с² - на поверхности Земли

Если обозначить R₀ радиус планеты, а h - расстояние до тела от поверхности планеты, то:

10) Гравитационная и инертная массы. Проверка ОТО. Проблема гравитационных волн.

Гравитационные и инертная масса равны друг другу (с высокой точностью — порядка 10⁻¹³ — экспериментально^[1][2], а в большинстве физических теорий, в том числе всех, подтверждённых экспериментально — точно), поэтому в том случае, когда речь идёт не о «новой физике», просто говорят о массе, не уточняя, какую из них имеют в виду.

Гравитационная масса показывает, с какой силой тело взаимодействует с внешними гравитационными полями (пассивная гравитационная масса) и какое гравитационное поле создаёт само это тело (активная гравитационная масса) — эта масса фигурирует в законе всемирного тяготения.

Инертная масса, которая характеризует меру инертности тел и фигурирует во втором законе Ньютона. Если произвольная сила в инерциальной системе отсчёта одинаково ускоряет разные тела, этим телам приписывают одинаковую инертную массу.

Гравитационная масса — характеристика материальной точки при анализе в классической механике, которая полагается причиной гравитационного взаимодействия тел, в отличие от инертной массы, которая определяет динамические свойства тел.

О́бщая тео́рия относи́тельности — геометрическая теория тяготения, развивающая специальную теорию относительности (СТО), опубликованная Альбертом Эйнштейном в 1915—1916 годах. В рамках общей теории относительности, как и в других метрических теориях, постулируется, что гравитационные эффекты обусловлены не силовым взаимодействием тел и полей, находящихся в пространстве-времени, а деформацией самого́ пространства-времени, которая связана, в частности, с присутствием массы-энергии. Общая теория относительности отличается от других метрических теорий тяготения использованием уравнений Эйнштейна для связи кривизны пространства-времени с присутствующей в нём материей.

ОТО в настоящее время — самая успешная теория гравитации, хорошо подтверждённая наблюдениями. Первый успех общей теории относительности состоял в объяснении аномальной прецессии перигелия Меркурия. Затем, в 1919 году, Артур Эддингтон сообщил о наблюдении отклонения света вблизи Солнца в момент полного затмения, что качественно и количественно подтвердило предсказания общей теории относительности. С тех пор многие другие наблюдения и эксперименты подтвердили значительное количество предсказаний теории, включая гравитационное замедление времени, гравитационное красное смещение, задержку сигнала в гравитационном поле и, пока лишь косвенно, гравитационное излучение^[4]. Кроме того, многочисленные наблюдения интерпретируются как подтверждения одного из самых таинственных и экзотических предсказаний общей теории относительности — существования чёрных дыр.

Несмотря на ошеломляющий успех общей теории относительности, в научном сообществе существует дискомфорт, связанный, во-первых, с тем, что её не удаётся переформулировать как классический предел квантовой теории, а во-вторых, с тем, что сама теория указывает границы своей применимости, так как предсказывает появление неустранимых физических расходимостей при рассмотрении чёрных дыр и вообще сингулярностей пространства-времени. Для решения этих проблем был предложен ряд альтернативных теорий, некоторые из которых также являются квантовыми. Современные экспериментальные данные, однако, указывают, что любого типа отклонения от ОТО должны быть очень малыми, если они вообще существуют.

Согласно принципу соответствия, в слабых гравитационных полях предсказания общей теории относительности совпадают с результатами применения ньютоновского закона всемирного тяготения с небольшими поправками, которые растут по мере увеличения напряжённости поля.

Первыми предсказанными и проверенными экспериментальными следствиями общей теории относительности стали три классических эффекта, перечисленных ниже в хронологическом порядке их первой проверки:

1. Дополнительный сдвиг перигелия орбиты Меркурия по сравнению с предсказаниями механики Ньютона.

2. Отклонение светового луча в гравитационном поле Солнца.

3. Гравитационное красное смещение, или замедление времени в гравитационном поле.

До сих пор надёжных экспериментальных свидетельств, опровергающих ОТО, не обнаружено. Отклонения измеренных величин эффектов от предсказываемых ОТО не превышают 0,01 % (для указанных выше трёх классических явлений). Несмотря на это, в связи с различными причинами теоретиками было разработано не менее 30 альтернативных теорий гравитации, причём некоторые из них позволяют получить сколь угодно близкие к ОТО результаты при соответствующих значениях входящих в теорию параметров.

11) Поля сил/векторные поля/. Напряженность гравитационного поля.

Полем сил называют область пространства, в каждой точке которого на помещенную туда частицу действует сила, закономерно меняющаяся от точки к точке. Примером может служить поле силы тяжести Земли или поле сил сопротивления в потоке жидкости (газа). Если сила в каждой точке силового поля не зависит от времени, то такое поле называют стационарным. Ясно, что силовое поле, стационарное в одной системе отсчета, в другой системе может оказаться и нестационарным. В стационарном силовом поле сила зависит только от положения частицы.

Работа, которую совершают силы поля при перемещении частицы из точки 1 в точку 2, зависит, вообще говоря, от пути. Однако среди стационарных силовых полей имеются такие, в которых эта работа не зависит от пути между точками 1 и 2. Этот класс полей, обладая рядом важнейших свойств, занимает особое место в физике. Рассмотрим свойства таких полей.

Определение: стационарное силовое поле, в котором работа силы поля на пути между двумя любыми точками не зависит от формы пути, а зависит только от положения этих точек, называется потенциальным, а сами силы - консервативными.

Если это условие не выполняется, то силовое поле не является потенциальным, а силы поля называют неконсервативными. К числу таких сил принадлежит, например, сила трения, так как работа этой силы зависит в общем случае от пути.

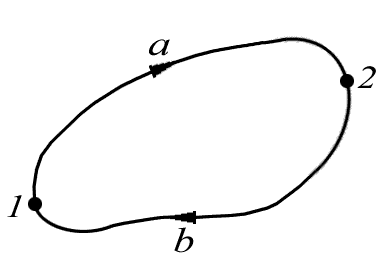
Покажем, что в потенциальном поле работа сил поля на любом замкнутом пути равна нулю. Действительно, любой замкнутый путь (рис. 5.5) можно разбить произвольно на две части: 1а2 и 2b1. Так как поле

Рис. 5.5.

Работа в потенциальном поле сил потенциально, то, по условию С другой стороны, очевидно, чтоПоэтому

что и требовалось доказать.

Наоборот, если работа сил поля на любом замкнутом пути равна нулю, то и работа этих сил на пути между произвольными точками 1 и 2 от формы пути не зависит, т. е. поле потенциально. Для доказательства выберем два произвольных пути: 1а2 и 1b2 (рис. 5.5). Составим из них замкнутый путь 1a2b1. Работа на этом замкнутом пути по условию равна нулю, т. е. ОтсюдаНо, поэтому

Таким образом, равенство нулю работы сил поля на любом замкнутом пути есть необходимое и достаточное условие независимости работы от формы пути, и может считаться отличительным признаком любого потенциального поля сил.

Рассмотрим важный случай поля центральных сил. Всякое силовое поле вызывается действием определенных тел. Сила, действующая на частицу А в таком поле, обусловлена взаимодействием этой частицы с данными телами. Если силы, зависят только от расстояния между взаимодействующими частицами и направлены по прямой, соединяющей эти частицы, от их называют центральными. Такими примерами служат силы гравитационные, кулоновские и упругие.

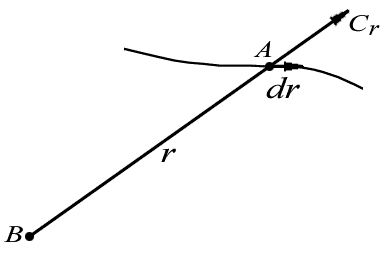
Центральную силу, действующую на частицу А со стороны частицы В, можно представить в общем виде:

,

(5.8)

где -функция, зависящая при данном характере взаимодействия только от r - расстояния между частицами;единичный вектор, задающий направление радиус-вектора частицы А относительно частицы В (рис.5.6).

Рис. 5.6. Работа в поле центральных сил

Докажем, что всякое стационарное поле центральных сил потенциально. Для этого найдем работу центральных сил в случае, когда силовое поле вызвано наличием одной неподвижной частицы B, а затем обобщим результат на произвольный случай. Элементарная работа силы (5.8)

на перемещении естьТак какпроекция векторана вектор, или на соответствующий радиус-вектор(рис. 5.6), тоРабота же этой силы на произвольном пути от точки 1 до точки 2

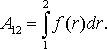
Полученное выражение зависит, очевидно, только от вида функции , т. е. от характера взаимодействия и от значений и- начального и конечного расстояний между частицамиA и B. От формы пути оно никак не зависит. Это и означает, что данное силовое поле потенциально.

Обобщим полученный результат на стационарное силовое поле, вызванное наличием совокупности неподвижных частиц, действующих на частицу A с силами .., каждая из которых является центральной. В этом случае работа результирующей силы при перемещении частицыA из одной точки в другую равна алгебраической сумме работ отдельных сил. А так как работа каждой из этих сил не зависит от формы пути, то и работа результирующей силы от нее также не зависит. Таким образом, действительно, любое стационарное поле центральных сил потенциально.

Введем понятие потенциальной энергии частицы в поле. То, что работа сил потенциального поля зависит только от начального и конечного положений частицы, дает возможность ввести чрезвычайно важное понятие потенциальной энергии.

Представим себе, что мы перемещаем частицу в потенциальном поле сил из разных точек P в фиксированную точку O. Так как работа сил поля не зависит от формы пути, то остается зависимость ее только от положения точки P (при фиксированной точке O ). А это значит, что данная работа будет некоторой функцией радиус-вектора r точки P.

Обозначив эту функцию , запишем

(5.9)

Функцию называютпотенциальной энергией частицы в данном поле.

Теперь найдем работу сил поля при перемещении частицы из точки 1 в точку 2 (рис. 5.7). Так как работа не зависит от пути, выберем путь,

Рис. 5.7. Введение понятия потенциальной энергии

проходящий через точку O. Тогда работа на пути 1O2 может быть представлена в виде

или с учетом (5.9)

(5.10)

Выражение, стоящее справа, есть убыль потенциальной энергии, т. е. разность значений потенциальной энергии частицы в начальной и конечной точках пути. Таким образом, работа сил поля на пути 1-2 равна убыли потенциальной энергии частицы в данном поле.

Изменение какой-либо произвольной физической величины X можно характеризовать либо ее приращением, либо убылью. Приращением величины X называют разность конечного и начальногозначений этой величины:

Приращение .

Убылью величины X называют разность ее начального и конечногозначений:

Убыль ,

т. е. убыль величины X равна ее приращению, взятому с обратным знаком. Приращение и убыль - величины алгебраические: если , то приращение положительно, а убыль отрицательна, и наоборот.

Очевидно, частице, находящейся в точке O поля, всегда можно приписать любое заранее выбранное значение потенциальной энергии. Это соответствует тому обстоятельству, что путем измерения работы может быть определена лишь разность потенциальных энергий в двух точках поля, но не ее абсолютное значение. Однако как только фиксирована потенциальная энергия в какой-либо точке, значения ее во всех остальных точках поля однозначно определяются формулой (5.10).

Формула (5.10) дает возможность найти выражение для любого потенциального ноля сил. Для этого достаточно вычислить работу, совершаемую силами поля на любом пути между двумя точками, и представить ее в виде убыли некоторой функции, которая и есть потенциальная энергия.

Именно так и было сделано при вычислении работы в полях упругой и гравитационной (кулоновской) сил, а также в однородном поле тяжести [см. формулы (5.3)- (5.5). Из этих формул сразу видно, что потенциальная энергия частицы в данных силовых нолях имеет следующий вид:

1) в поле упругой силы

(5.11)

2) в поле точечной массы (заряда)

(5.12)

где для гравитационного взаимодействия идля кулоновского взаимодействия;

3) в однородном поле сил тяжести

(5.13)

Еще раз подчеркнем, что потенциальная энергия - это функция, которая определяется с точностью до прибавления некоторой произвольной постоянной. Это обстоятельство, однако, совершенно несущественно, ибо во все формулы входит только разность значенийв двух положениях частицы. Поэтому произвольная постоянная, одинаковая для всех точек поля, выпадает. В связи с этим ее обычно опускают, что и сделано в трех предыдущих выражениях.

Отметим еще одно важное обстоятельство. Потенциальную энергию следует относить не к частице, а к системе взаимодействующих между собой частицы и тел, вызывающих силовое поле. При данном характере взаимодействия потенциальная энергия взаимодействия частицы с данными телами зависит только от положения частицы относительно этих тел.

Определим связь потенциальной энергии и силы поля. Взаимодействие частицы с окружающими телами можно описывать двумя способами: с помощью сил или с помощью потенциальной энергии. В классической механике оба способа используют одинаково широко. Однако первый способ обладает несколько большей общностью, ибо он применим и к таким силам, для которых нельзя ввести потенциальную энергию (например, к силам трения). Второй же способ применим только в случае консервативных сил.

Наша задача - установить связь между потенциальной энергией и силой поля, точнее, определить поле сил по заданной потенциальной энергиикак функции положения частицы в поле.

Ранее было показано, что при перемещении частицы из одной точки потенциального поля в другую работа, которую производят силы поля, может быть представлена как убыль потенциальной энергии частицы, т. е. Это относится и к элементарному перемещениюили

(5.14)

Учитывая, что , где- элементарный путь, перепишем уравнение(5.14) в форме

где - это убыль потенциальной энергиив направлении перемещения. Отсюда

(5.15)

т. е. проекция силы поля - вектора - в данной точке на направление перемещенияравна с обратным знаком производной потенциальной энергиипо данному направлению. Символ-частной производной - подчеркивает, что производная берется по определенному направлению.

Перемещение мы можем взять в любом направлении, в частности вдоль координатных осей х, у, z. Если перемещение, например, параллельно оси х, то его можно представить так:гдеорт осиприращение координаты. x. Тогда paбота силына перемещении, параллельном оси x,

где проекция векторана орта не на перемещение, как в случае

Подставив последнее выражение в уравнение (5.14), получим

где символ частной производной означает, что потенциальная энергия при дифференцировании должна рассматриваться как функция одного аргумента х, остальные же аргументы должны оставаться при этом постоянными. Ясно, что для проекцийиуравнения будут аналогичны уравнению для.

Итак, взяв с обратными знаками частные производные функции U по х, у и z, мы найдем проекции ивекторана орты. Отсюда легко найти и сам вектор:или

Величину, стоящую в скобках, называют градиентом скалярной функции U и обозначают илиМы будем пользоваться вторым, более удобным, обозначением, где значок"набла" означает символический векторный оператор

.

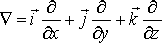Поэтому формально можно рассматривать как произведение символического векторана скаляр.

Таким образом, связь между силой поля и потенциальной энергией как функцией координат можно представить в следующем компактном виде:

(5.16)

т. е. сила поля равна со знаком минус градиенту потенциальной энергиичастицы в данной точке поля. Можно сказать и проще: сила поля F равна антиградиенту потенциальной энергии. Последняя формула дает возможность, зная функцию , восстановить поле сил.

Пример. Потенциальная энергия частицы в некотором поле имеет вид:

а) гдепостоянная;

б) гдепостоянный вектор,радиус-вектор точки поля

Найдем соответствующее каждому случаю поле сил:

а)

б) представим сначала функцию U в виде ; тогда

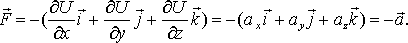
Смысл градиента станет нагляднее и яснее, если ввести понятие эквипотенциальной поверхности - поверхности, во всех точках которой потенциальная энергия U имеет одно и то же значение. Ясно, что каждому значению U соответствует своя эквипотенциальная поверхность.

Из формулы (5.15) следует, что проекция вектора на любое направление, касательное к эквипотенциальной поверхности в данной точке, равна нулю. Это значит, что векторнормален эквипотенциальной поверхности в данной точке. Далее, возьмем перемещениев сторону уменьшенияU, тогда U меньше 0, и, согласно (5.15), т.е. векторнаправлен в сторону уменьшения U. А так какпротивоположен по направлению вектору, то мы приходим к выводу, чтоградиент U - это вектор, направленный по нормали к эквипотенциальной поверхности в сторону возрастания потенциальной энергии U.

Рис. 5.8. Эквипотенциальные поверхности и направление силы

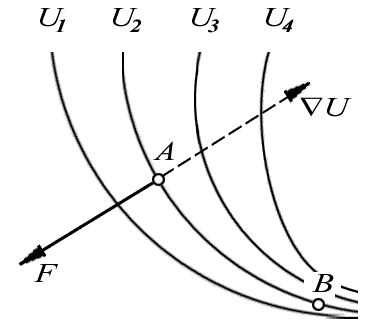
Сказанное поясняет рис. 5.8, относящийся к двумерному случаю. На

нем изображена система эквипотенциалей , a также градиент потенциальной энергии U и соответствующий вектор силыв точке А поля. Полезно подумать, какими будут векторы этих двух величин, например, в точке В данного поля.

В заключение заметим, что можно говорить о градиенте не только функции U, но и любой другой скалярной функции координат. Понятие градиента широко используется в самых различных разделах физики, особенно в теории электромагнетизма.

Рассмотрим понятие поля сил. Опыт показывает, что в случае гравитационных и электростатических взаимодействий сила , действующая на частицу А со стороны окружающих тел (системы В), пропорциональна массе (или заряду) частицы А Другими словами, силаможет быть представлена в виде произведения двух величии:

,

(5.17)

где m-масса (или заряд) частицы A, - некоторый вектор (для гравитационных сил вблизи поверхности Земли он совпадает с вектором ускорения свободного падения), зависящий как от положения частицы А, так и от свойств окружающих тел - системы В.

Такое представление силы открывает возможность иной физической интерпретации взаимодействия, связанной с понятием поля. А именно: в этом случае говорят, что система В создает в окружающем пространстве поле, характеризуемое вектором . По-другому можно сказать, .что в каждой точке пространства система В - источник поля - создает такие условия (вектор), при которых частица, помещенная в эти точки, испытывает действие силы(5.17). Причем считают, что поле (вектор ) существует безотносительно к тому, есть ли в нем частица А или нет. При рассмотрении стационарных случаев, понятие поля может рассматриваться как чисто условное (формальное), введенное лишь для удобства описания явлений. Однако при переходе к переменным полям выясняется, что понятие поля имеет глубокий физический смысл: поле есть физическая реальность.

Вектор называютнапряженностью поля. Одно из важнейших свойств полей заключается в том, что поле, образованное несколькими источниками, равно сумме полей, созданных каждым из них. Точнее, напряженность G результирующего поля в произвольной точке

(5.18)

где - напряженность поля соответствующего источника в этой же точке. Эта формула выражает так называемыйпринцип суперпозиции (или наложения) полей, который является отражением опытных фактов и дополняет законы механики.

Обратимся теперь к потенциальной энергии частицы. Согласно (5.17),

формулу (5.14) можно записать так: Поделив обе части нат и обозначив получим

(5.19)

или

(5.20)

Функцию называютпотенциалом поля в точке с радиус-вектором .

Формула (5.20) дает возможность, в частности, найти потенциал любого гравитационного и электростатического полей. Для этого достаточно вычислить интеграл по произвольному пути между точками1 и 2 и представить затем полученное выражение в виде убыли некоторой функции, которая и есть потенциал . Так, потенциалы гравитационного ноля точечной массыт и кулоновского поля точечного заряда q определяются, согласно (5.12), формулами

(5.21)

Заметим, что потенциал , как и потенциальная энергия, может быть определен только с точностью до прибавления некоторой произвольной постоянной, также совершенно несущественной. Поэтому ее обычно опускают, полагая равной нулю.

Итак, поле можно описывать или в векторном виде , или в скалярном. Оба способа эквиваленты. Практически же оказывается, что второй способ описания поля с помощью потенциалав большинстве случаев значительно удобнее. Этому есть несколько причин.

1. Зная , можно немедленно вычислить потенциальную энергиюU и работу сил поля A:

(5.22)

2. Вместо трех компонент векторной функции проще задавать скалярную функцию.

3. Когда поле создается многими источниками, потенциал рассчитывать легче, чем вектор: потенциалы - скалярные величины, их можно просто складывать, не заботясь о напрвлении сил. Действительно, согласно(5.18) и (5.19), то есть

(5.23)

где потенциал, создаваемыйчастицей в данной точке поля.

4. И наконец, зная функцию , можно легко восстановить поле- как антиградиент потенциала:

(5.24)

Эта формула непосредственно следует из (5.16).

В заключение рассмотрим пример на нахождение потенциала поля центробежных сил инерции.

Пример. Найдем напряженность и потенциалполя центробежных сил инерции в системе отсчета вращающейся вокруг неподвижной оси с постоянной угловой скоростью.

Напряженность гдерадиус-вектор точки поля относительно оси вращения.

Теперь, согласно (5.20), найдем интеграл от по пути от точки 1 до точки 2:

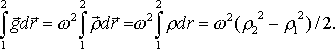
Видно, что этот интеграл от формы пути между точками 1 и 2 не зависит,

а зависит только от положения данных точек. Это означает, что рассматриваемое поле сил является потенциальным.

Из сравнения полученного результата с (5.20) следует, что

(5.25)

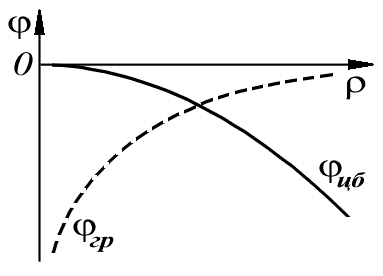
На рис. 5.9 показан график зависимости от расстояния до оси

Рис. 5.9. Зависимость центробежного потенциала от расстояния до оси вращения

вращения. Здесь же для сравнения показан и график потенциала гравитационного поля точечной массы, находящейся в точке

Векторное поле — это отображение, которое каждой точке рассматриваемого пространства ставит в соответствие вектор с началом в этой точке. Например, вектор скорости ветра в данный момент времени изменяется от точки к точке и может быть описан векторным полем.

Евклидово пространство

Векторное поле на евклидовом (или псевдоевклидовом) пространстве^[1] определяется каквектор-функция точки пространства, отображающая это пространство в (на) себя^[2]:

То есть, каждой точке пространства сопоставляется некоторый вектор (значение векторного поля в данной точке пространства). В общем случае этот вектор различается для разных точек пространства, то есть в общем случае векторное поле принимает разные значения в разных точках пространства. В каждой точке пространства вектор поля имеет определенную величину и определенное (за исключением тех случаев, когда поле обращается в ноль) направление в этом пространстве^[3].

В литературе (особенно в более старой, а также в физической) применительно к векторному полю на некотором пространстве употребляется также предлог в (т.е. говорят и поле на пространстве, и поле в пространстве).

Многообразие

В более общем случае, когда исходное пространство является многообразием, векторное поле определяется как сечение касательного расслоения к данному многообразию, то есть отображение, которое каждой точке ставит в соответствие векториз касательного пространства в.

В физике

В физике термин векторное поле, кроме общего значения, описанного выше, имеет специальное значение, в основном в отношении фундаментальных полей (см. ниже). Смысл этого употребления сводится к тому, что фундаментальные физические поля классифицируются по природе их потенциала, и один из таких типов — векторные поля (как электромагнитное или глюонное поля).

Напряжённость гравитацио́нного по́ля — векторная величина, характеризующая гравитационное поле в данной точке и численно равная отношению силы тяготения, действующей на тело, помещённое в данную точку поля, к гравитационной массе этого тела:

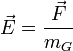
Свойства

Если источником гравитационного поля является некое гравитирующее тело, то согласно закону всемирного тяготения:

где:

—гравитационная постоянная;

—гравитационная масса тела-источника поля;

—расстояние от исследуемой точки пространства до центра масс тела-источника поля.

Применяя второй закон Ньютона и принцип эквивалентности гравитационной и инерционной масс:

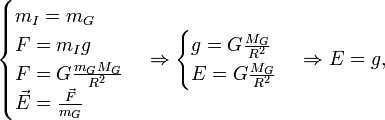
то есть напряжённость гравитационного поля численно (и по размерности) равна ускорению свободного падения в этом поле.

12) Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек) тела или системы^[1].

Определение

В механике можно ввести понятие работы, исходя из довольно простых представлений^[2]

Работа силы (сил) над одной точкой

Работа нескольких сил определяется естественным образом как работа их равнодействующей (их векторной суммы). Поэтому дальше будем говорить об одной силе.

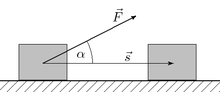
При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения^[3]:

Здесь точкой обозначено скалярное произведение^[4], —вектор перемещения; подразумевается, что действующая сила постоянна в течение всего того времени, за которое вычисляется работа.

Если сила не постоянна, то в этом случае она вычисляется как интеграл^[5]:

(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений если вначале считать их конечными, а потом устремить длину каждого к нулю).

Если существует зависимость силы от координат^[6], интеграл определяется^[7] следующим образом:

,

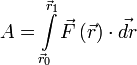где и—радиус-векторы начального и конечного положения тела соответственно.

Cледствие: если направление движения тела ортогонально силе, работа (этой силы) равна нулю.

Работа силы (сил) над системой или неточечным телом

Работа сил над системой материальных точек определяется как сумма работ этих сил над каждой точкой (работы, совершённые над каждой точкой системы, суммируются в суммарную работу этих сил над системой).

Даже если изначально тело не является системой дискретных точек, можно разбить его (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых считать материальной точкой, вычисляя работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл.

Эти определения могут быть использованы как для какой-то конкретной силы или класса сил — для вычисления именно их работы отдельно, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.

Кинетическая энергия

Кинетическая энергия вводится в механике в прямой связи с понятием работы.

Схема рассуждений такова: 1) попробуем записать работу, совершаемую всеми силами, действующими на материальную точку и, пользуясь вторым законом Ньютона (позволяющим выразить силу через ускорение), попытаться выразить ответ только через кинематические величины, 2) убедившись, что это удалось, и что этот ответ зависит только от начального и конечного состояния движения, введём новую физическую величину, через которую эта работа будет просто выражаться (это и будет кинетическая энергия).

Если — полная работа, совершённая над частицей, определяемая как сумма работ совершенных приложенными к частице силами, то она выражается как:

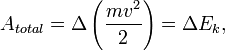
где называетсякинетической энергией. Для материальной точки, кинетическая энергия определяется как работа силы, ускорившей точку от нулевой скорости до величины скорости и выражается как:

Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.

Потенциальная энергия

Сила называется потенциальной, если существует скалярная функция координат, известная как потенциальная энергия и обозначаемая , такая что

Если все силы, действующие на частицу консервативны, и является полной потенциальной энергией, полученной суммированием потенциальных энергий соответствующих каждой силе, тогда:

.

Этот результат известен как сохранение механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы

является постоянной относительно времени. Этот закон широко используется при решении задач классической механики.

Работа в термодинамике

Основная статья: Термодинамическая работа

В термодинамике работа, совершенная газом при расширении^[8], рассчитывается как интеграл давления по объёму:

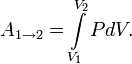
Работа, совершенная над газом, совпадает с этим выражением по абсолютной величине, но противоположна по знаку.

Естественное обобщение этой формулы применимо не только к процессам, где давление есть однозначная функция объема, но и к любому процессу (изображаемому любой кривой в плоскости PV), в частности, к циклическим процессам.

В принципе, формула применима не только к газу, но и к чему угодно, способному оказывать давление (надо только чтобы давление в сосуде было всюду одинаковым, что неявно подразумевается в формуле).

Эта формула прямо связана с механической работой. Действительно, попробуем написать механическую работу при расширении сосуда, учитывая, что сила давления газа будет направлена перпендикулярно каждой элементарной площадке, равна произведению давления P на площадь dS площадки, и тогда работа, совершаемая газом для смещения h одной такой элементарной площадки будет

Видно, что это и есть произведение давления на приращение объема вблизи данной элементарной площадкой. А просуммировав по всем dS получим конечный результат, где будет уже полное приращение объема, как и в главной формуле параграфа.

Работа силы в теоретической механике

Рассмотрим несколько детальнее, чем это было сделано выше, построение определения энергии как риманова интеграла.

Пусть материальная точка движется по непрерывно дифференцируемой кривой, где s — переменная длина дуги,и на неё действуетсила , направленная по касательной к траектории в направлении движения (если сила не направлена по касательной, то будем понимать подпроекцию силы на положительную касательную кривой, таким образом сведя и этот случай к рассматриваемому далее). Величина, называетсяэлементарной работой силы на участкеи принимается за приближенное значение работы, которую производит сила, воздействующая на материальную точку, когда последняя проходит кривую. Сумма всех элементарных работ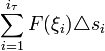является интегральной суммой Римана функции.

В соответствии с определением интеграла Римана, можем дать определение работе:

Предел, к которому стремится сумма 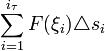всех элементарных работ, когда мелкостьразбиениястремится к нулю, называется работой силывдоль кривой.

Таким образом, если обозначить эту работу буквой , то, в силу данного определения,

,

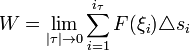следовательно,

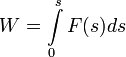(1).

Если положение точки на траектории её движения описывается с помощью какого-либо другого параметра (например, времени) и если величина пройденного пути,является непрерывно дифференцируемой функцией, то из формулы (1) получим

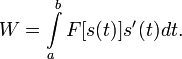
Размерность и единицы

Единицей измерения работы в СИ является Джоуль, в СГС — эрг

1 Дж = 1 кг·м²/с² = 1 Н·м

1 эрг = 1 г·см²/с² = 1 дин·см

1 эрг = 10⁻⁷ Дж

Мо́щность — физическая величина, равная в общем случае скорости изменения энергии системы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.

Различают среднюю мощность за промежуток времени

и мгновенную мощность в данный момент времени:

Интеграл от мгновенной мощности за промежуток времени равен полной переданной энергии за это время:

Содержание

1 Единицы измерения

2 Мощность в механике

3 Электрическая мощность

4 Приборы для измерения мощности

5 См. также

6 Ссылки

Единицы измерения

В системе СИ единицей измерения мощности является ватт, равный одному джоулю, делённому на секунду.

Другой распространённой единицей измерения мощности является лошадиная сила.

Соотношения между единицами мощности
Единицы	Вт	кВт	МВт	кгс·м/с	эрг/с	л. с.(мет.)	л. с.(анг.)
1 ватт	1	10^−3	10^−6	0,102	10^7	1,36·10^−3	1,34·10^−3
1 киловатт	10^3	1	10^−3	102	10^10	1,36	1,34
1 мегаватт	10^6	10^3	1	102·10^3	10^13	1,36·10^3	1,34·10^3
1 килограмм-сила-метр в секунду	9,81	9,81·10^−3	9,81·10^−6	1	9,81·10^7	1,33·10^−2	1,31·10^−2
1 эрг в секунду	10^−7	10^−10	10^−13	1,02·10^−8	1	1,36·10^−10	1,34·10^−10
1 лошадиная сила (метрическая)	735,5	735,5·10^−3	735,5·10^−6	75	7,355·10^9	1	0,9863
1 лошадиная сила (английская)	745,7	745,7·10^−3	745,7·10^−6	76,04	7,457·10^9	1,014	1

Мощность в механике

Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:

где F — сила, v — скорость, — угол между вектором скорости и силы.

Частный случай мощности при вращательном движении:

M — момент силы, — угловая скорость,— числопи, n — частота вращения (число оборотов в минуту, об/мин.).

Электрическая мощность

Основная статья: Электрическая мощность

Электри́ческая мощность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии. При изучении сетей переменного тока, помимо мгновенной мощности, соответствующей общефизическому определению, вводятся также понятия активной мощности, равной среднему за период значению мгновенной, реактивной мощности, которая соответствует энергии, циркулирующей без диссипации от источника к потребителю и обратно, и полной мощности, вычисляемой как произведение действующих значений тока и напряжения без учёта сдвига фаз.

13) Кинети́ческая эне́ргия — энергиямеханической системы, зависящая отскоростейдвижения её точек. Часто выделяют кинетическую энергиюпоступательного и вращательного движения.

Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.

Содержание

1 История

2 Физический смысл

3 Физический смысл работы

4 Релятивизм

5 Соотношение кинетической и внутренней энергии

6 См. также

История

Впервые понятие кинетической энергии было введено в трудах Г. Лейбница, посвященных понятию «живой силы»

Физический смысл

Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона:

—есть результирующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы . Учитывая, что, Получим:

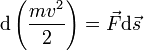
Если система замкнута, то есть , то, а величина

остаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия является интегралом движения.

Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

где:

—масса тела

—скорость центра масс тела

—момент инерции тела

—угловая скорость тела.

Физический смысл работы

Работа всех сил, действующих на частицу, идёт на приращение кинетической энергии частицы:

Релятивизм

При скоростях, близких к скорости света, кинетическая энергия любого объекта равна

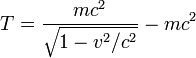
где:

—масса объекта;

—скорость движения объекта в инерциальной системе отсчета;

—скорость света в вакууме (—энергия покоя).

Данную формулу можно переписать в следующем виде:

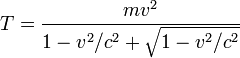
При малых скоростях () последнее соотношение переходит в обычную формулу.

Соотношение кинетической и внутренней энергии

Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров), то тело неподвижно как единое целое, и можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.

То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов и молекул, и внутренняя энергия обусловлена движением атомов и молекул и рассматривается как следствие теплового движения этих частиц, а абсолютная температура тела прямо пропорциональна средней кинетической энергии такого движения атомов и молекул. Коэффициент пропорциональности — Постоянная Больцмана.

14) Если тело перемещается в гравитационном поле на значительное расстояние, то совершаемую против сил гравитационного притяжения работу (например, работу для вывода ракеты в космос) нельзя вычислить по формуле W=G·h, потому, что сила тяжести G обратно пропорциональна расстоянию между центрами масс.

Работа, совершаемая при перемещении тела вдоль радиуса в гравитационном поле, определяется как интеграл

Здесь: W — работа против гравитационной силы (Джоуль), G — гравитационная сила, с которой два тела притягиваются друг к другу (Ньютон), m_a — масса первого тела (кг), m_b — масса второго тела (кг), r — расстояние между центрами масс тел (метр), r₁ — начальное расстояние между центрами масс тел (метр), r₂ — конечное расстояние между центрами масс тел (метр), γ — гравитационная постоянная 6.67 · 10^-11 (м³/(кг · сек²)),

Величина работы W не зависит от формы пути от точки r₁ к r₂, так как в формулу входят только радиальные составляющие dr перемещения, совпадающие с направлением силы притяжения.

формула (3) справедлива в случае любых небесных тел.

15) Потенциальным называется поле, работа которого при переходе из одной точки поля в другую не зависит от формы траектории. Потенциальными являются поле силы тяжести и электростатическое поле.

Потенциальное поле - это поле, в котором работа силы не зависит от формы пути, а зависит лишь от положений начальной и конечной точек траектории, а силы, действующие в нем, - консервативными.

Консервативные (потенциальные) силы - это силы, зависящие только от координат точек системы и работа которых не зависит от пути перехода из начального в конечное положение, а определяется только начальным и конечным положением.

В потенциальном поле работа сил по любому замкнутому контуру равна нулю.

Связь между силовой и энергетической характеристиками в потенциальном силовом поле.

В потенциальном силовом поле и E и F являются функциями координат. Пусть сила F направлена вдоль перемещения, тогда приращение Ep:

-dE = Fdr = Frdr

Fr = -dEp/dr

"-" указывает на то, что сила направлена в сторону убывания потенциальной энергии.

В случае, когда вектор F имеет произвольное направление в пространстве, необходимо поставить в соответствие сколярному полю Ep вектор F.

Эту задачу решает градиент:

F = - grad Ep.

Потенциальная энергия —скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы^[1]. Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином.

Единицей измерения энергии в СИ является Джоуль, в СГС — эрг.

Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии.

Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными.

Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля.

Любая физическая система стремится к состоянию с наименьшей потенциальной энергией.

Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела.