Экзамен по ЧМРТЗ

Тема 1. Численные методы. Область использования. Преимущества, недостатки.

Большинство реальных задач описываются системами сложных уравнений, отражающих тот или иной реальный процесс. Модели, которые используются для реальных процессов и установок весьма сложны. Решение их поэтому затруднено из-за большого числа входящих в них элементов. Кроме того эти модели часто не имеют полной информации о входящих в них величинах. Для теоретических исследований поэтому используются вычислительные эксперименты. На первом этапе формулируется решаемая задача (выбирается физическая модель процесса), этой модели ставится в соответствие математическая модель (описание процесса с помощью алгебраических, дифференцальных и других уравнений), затем выбирается метод решения (аналитический или численный), осуществляется решение и анализ полученных результатов.

Вычислительный эксперимент.
физическая модель
	↓
математическая модель
	↓
выбор математического решения
численные методы	↓	аналитическое
↓

представление задачи в удобном для решения виде

↓

составление блок-схемы

↓

программирование задачи

↓

решение

↓

проверка

↓

анализ

Основные требования, представляемые к вычислительному алгоритму:

1.Точность. Алгоритм должен давать решение задач с заданной точностью. Увеличение точности ведѐт к увеличению времени вычисления.

2.Экономичность. Среди эквивалентных по порядку точности алгоритмов выбирают тот, который даѐт решение с затратой наименьшего машинного времени.

3.Отсутствие аварийного останова в процессе вычислений. Если получаемые значения слишком велики или малы, то происходит останов ЭВМ вследствии переполнения разрядной сетки.

Численные методы дают приближенное решение задач, т.е. вместо точного решения находят решение другой задачи, близкое к искомому.

К преимуществам численных методов относятся:

1)низкая стоимость (по сравнению с экспериментом);

2)возможность получения результатов решения по многим вариантам за короткое время;

3)полнота получаемой информации;

4)возможность математического моделирования любых реальных объектов.

Численные методы обычно содержат погрешности. Источники погрешностей: (1,2 – неустранимые)

1)Несоотвествие математической модели изучаемому реальному явлению. Вопрос соответствия проверяется путѐм сравнения экспериментальных данных и решений данной модели.

2)Погрешность исходных данных. Влияние еѐ можно установить варьируя исходные данные в пределах погрешности.

3)Погрешность метода решения. Даже при соотвествии математической модели получаемому явлению и высокой точности исходных данных возникает погрешность метода. Это происходит потому что решается другая более простая задача, приближѐнная к исходной. Часто численный метод строится на бесконечном процессе, который приводит к искомому решению, но реально предельный переход не удаѐтся осуществить и процесс прерывается, получается приближѐнное значение.

4)Погрешность округления в арифметических и других действиях над числами. Если количество выполняемых арифметических действий невелико, то погрешность не проявляется.

Методы решения алгебраических и трансцендентных уравнений:

↓

	однородные				система уравнений
линейные	↓	нелинейные		линейные (1 решение) ↓		нелинейные(несколько
	алгебраические ↓		трансцендентные			решений)

Нелинейные уравнения, содержащие тригонометрические функции или другие называются трансцендентными.

Пример: sinx+2=0 3 + = 0

Решаемая задача состоит в отыскаии корней уравнения (нулей) f(x)=0.

Если функция представляет многочлен, то уравнение называется алгебраическим.

0 + 1 + 2 2 + + = 0

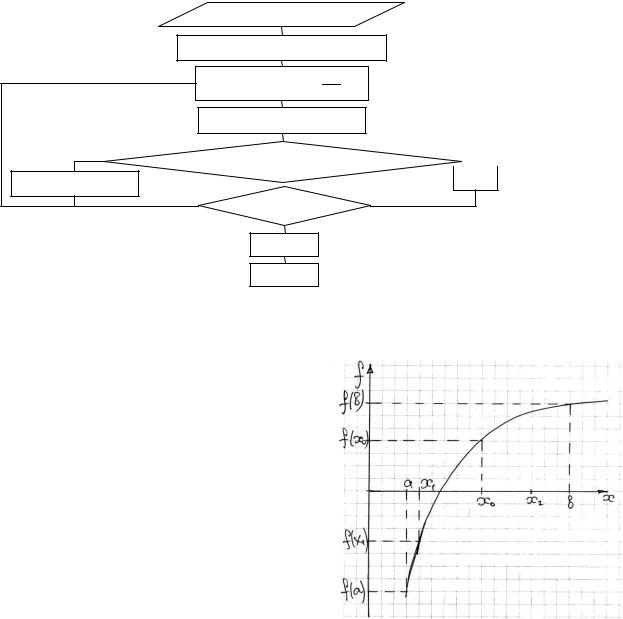
Тема 2. Метод половинного деления. Дихотомия.

Считают, что известен отрезок ab, внутри которого существует и расположен один корень. Условие единственности:

1)	∙ = ;
2)	′′ не меняет знак на	, .

Метод используется тогда, когда вид функции f(x) достаточно схожий. Этот метод хоть и требует большого объѐма вычислений, но всегда приводит к искомому результату.

Исходный отрезок ab делится пополам, находится значение функции в x0; находят функцию в точке a или b и преверяют знак произведения 0 ∙ .

Если знаки совпадают, то выбирают противоположный отрезок, делят его пополам и т.д. Интервал, в котором находится корень, сужается. Процесс деления происходит до тех пор, пока длина отрезка, на котором находится корень, не будет меньше наперед заданной погрешности ε. − − ≤

Нет

Да

b=x0 ∙ 0

Ввод данных (ε, a, b)

Нахождение функции f(a), f(b)

Средняя точка 0 = +2

Нахождение нулей f(x0)

Нет Проверка 0 ∙ < 0

a=x

b − a ≤ ε

Да

Печать

Конец

Изложенный метод является типичным машинным, так как вычисления просты и цикличны, метод устойчив к ошибкам округления, обладает хорошей сходимостью после того как впервые найден интервал, на котором находится корень, его ширина после n-итераций убывает в 2n-раз. Но скорость сходимости невелика.

Пример:

−

1 − 3 = 0

0; 1

= 0,1

= 0+1 = 0,5

0

2

0

=

0 − 1 − 0 = 0

1

=

1 − 1 − 3 ∙ 1 = 0,16

0,5 −

1 − 3 ∙ 0,5 = −0,422

= 1+0,5 = 0,75

0

2

0,75

= 0,75 − 1 − 3 ∙ 0,75 = −0,13

= 0,75+1 = 0,875

2

2

0,875 = 0,875 −

1 − 3 ∙ 0,875 = −0,016

= 0,875+1 = 0,9375

3

2

Тема 3. Метод Ньютона. Метод секущих.

1 Метод Ньютона (касательных)

Этот метод эффективен для тех уравнений, длякоторых значение модуля f′ x по абсолютной величине вблизи корня достаточно велико, т.е. график функции в окресностях корня имеет большую крутизну.

В основе метода лежит разложение функции f(x) в ряд Тейлора у окресности точки xn.

f xn + h = f xn	+ hf′ x +	h2	f′′	x +	h = xn+1 − xn – шаг.
	2

Ввиду малости h слагаемое, содержащее h в квадрате и большей степени, может быть отброшено: f xn + h = f xn + hf′ xn

+ = + + − ′

Предположим, что переход от xn к xn+1 приближает значение функции к нулю, так что f xn + h = 0, тогда

+ = − ′

Значение xn+1 соотвествует точке, в которой касательная к точке xn пересекает ось Ох.

xn − xn−1 ≤ ε

ε, xn, n=0

f(xn), f’(xn)

+1 = − ′

		−	≤	Да
					Печать	Конец
		−1

Нет

xn = xn+1

n = n + 1

Пример:

x −

1 − 0,3x

= 0

0; 1

ε = 0,1

f′

x = 1 +

0,3

2

1−0,3x

0,3

x0

= 0

f x0

= 0 −

1 − 0,3 ∙ 0 = −1 f′ x0

= 1 +

= 1,15

2

1−0,3∙0

x

= 0 −

−1

= 0,869

1

1,15

x2

= 0,869 −

0,869−

1−0,3∙0,869

= 0,861

1+

0,3

2

1−0,3∙0,869

n=2

2 Метод секущих Если определение производной функции затруднено, то можно воспользоваться некоторым приближением, а именно

	′			− −
				−−

Подставим е в формулу Ньютона:

xn+1	= xn − f xn	xn −xn−1
	f xn	−f xn−1

Для определения новой точки требуются две предыдущие. Метод уступает методу Ньютона по скорости сходимости, но его преимущество – не требуется определение производной.

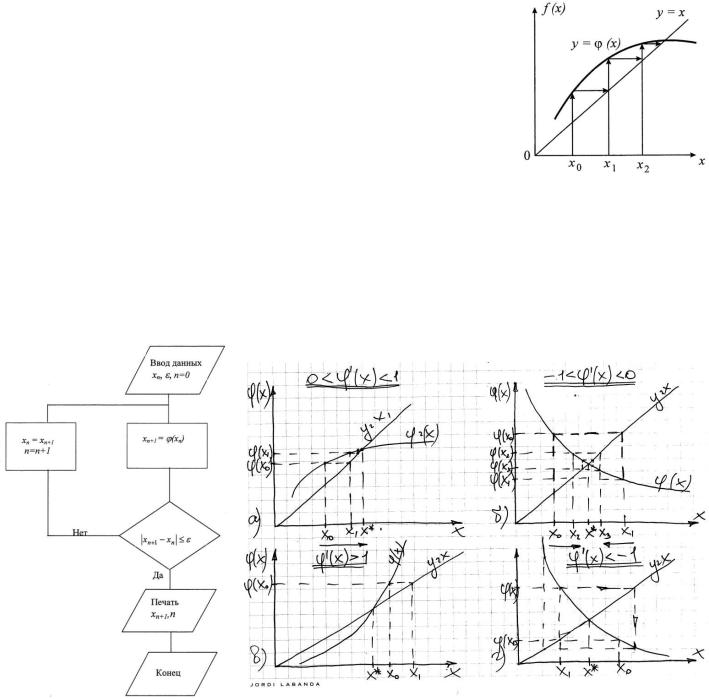
Тема 4. Метод простой итерации.

Численный метод, в котором шаг за шагом производится уточнение первоначального приближения, называется методом итераций. Каждый шаг называется итерацией. Если в результате итерирования получают значения, которые всѐ ближе к истинному значению корня, то говорят, что метод итерации сходится. n – число итераций.

Для использования метода простой итерации необходимо исходное уравнение( ) = 0 переписать в виде = (1), выразив x1 в левой части.

3 + sin = 0	= −	sin
	3
Это можно сделать многими способами, например, выделив x, а остальное
перенеся в левую часть или умножив обе части исходного уравнения на
некоторую константу λ и прибавив к обеим частям x.
+ = (2)		= +		′ = ′ + 1 (3)
φ(x) стараются выбрать так, чтобы производная от неѐ была меньше 1 ′					< 1, тогда корень уравнения будет

всегда найден. Продифференцируем (3) по x. Наиболее высокая скорость сходимости будет в том случае, если

	′		= 0, тогда = −		1	. Подставим значение λ в (2), тогда = −		– формула Ньютона. Следовательно
				′			′

метод Ньютона является наиболее быстросходящимся из итерационных методов.

Метод итерации заключается в следующем: на известном интервале выбирается любое x0 и через него находится функция φ: 1 = 0 . Значения этих величин сравнивают по абсолютной величине: 0 − 1 ≤ . Если это условие выполняется, то x считается корнем уравнения. Если нет, то x0=x1 и продолжают до выполнения условия.

′

< – сходится;

′

> 1 – расходится;

Пример:

−

0; 1

= 0,1

1 − 0,3

= 0

Проверка: ′

0,3

′

′ 1 = −0,18

=

1 − 0,3

= −

0 = −0,15

2

1−0,3

x0=1 x0=0,837

x0=0,865

x1=0,837	x1≠x0
x1=0,865	x1≠x0
x1=0,861	0 − 1 ≤ 0,01

n=3

Скорость сходимости метода итерации зависит от удачности выбора нулевого приближения. Метод итерации с коэффициентом.

Сходимость метода простой итерации можно увеличить, если последующее значение x принимать в виде

		= +				=	−	=	1	– поправка.
+1									′
	а)		1<α<∞
	б)		½<α<1
	в)		α<0
	г)		0<α<½

Метод итерации с коэффициентом улучшает сходимость. А в некоторых случаях, когда метод итерации расходится, то позволяет получить корень уравнения.

Тема 5. Понятие обусловленных и плохообусловленных матриц.

Система n-уравнений с n-неизвестными, каждое слагаемое которой содержит только одно неизвестное и оно входит в уравнение в первой степени, называется линейной.

+ + + +					=
11	1	12 2	13 3	1			1
+ + + + =								(1)
21	1	22 2	23 3	2			2
… + + + + + + + =
+ + + +						=
1 1		2 2	3 3
Ax=B	11	12	… 1			1
									1
	21	22	… 2			2
=	… …		… … ;	=		… ;		=	2
									…
			…
	1	2

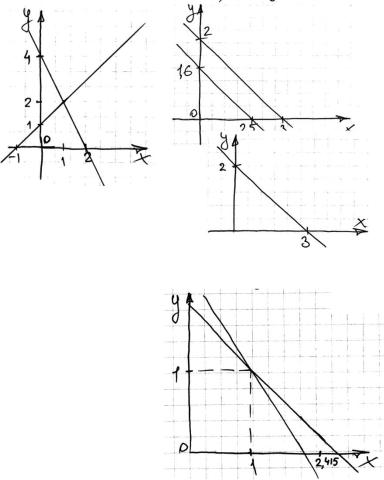
Для произвольной системы уравнений без предварительного исследования нельзя сказать, имеет ли она (система) решения и является ли оно единственным.

1.Решение существует, оно единственное

2 + = 4

− = −1

2.Не имеет решений

4 + 6 = 10

2 + 3 = 6

3. Бесконечное количество решений

4 + 6 = 12

2 + 3 = 6

Системы типа 2 и 3 являются вырожденными.

Если определитель равен нулю, то система вырожденная.

С точки зрения практических вычислений могут существовать «почти» вырожденные системы. При их решении получают недостоверные значения неизвестных.

При задании невысокой точности после окргуления могут получаться решения, не лежащие ни на одной из линий, но очень близкие к ним.

Пример:

5 + 7 = 12

7 + 10 = 17

Решение: x=y=1,

но x=2,415 и у=0 удовлетворяют решению при заданной точности

5*2,415+7*0=12,075

7*2,415+10*0=16,905

Такие системы называют плохообусловленными.

Тема 7. Метод исключения Гаусса для решения СЛАУ.

Основан на последовательном исключении неизвестных x1, x2 и т.д. xn-1 и получении в конечном итоге одного уравнения с xn. Одновременно осуществляется преобразование системы, которое позволяет после определения xn

последовательно найти xn-1, xn-2 и т.д. x1.

11 1 + 12 2 + 13 3 = 1 − 121 1 + 22 2 + 23 3 = 2 − 2 (1)31 1 + 32 2 + 33 3 = 3 − 3

Если a11=0, то уравнения надо представить так, чтобы коэффициент при x1 в первом уравнении не равнялся нулю. Прямой ход:

1. = домножаем 1 на ω2 и вычитаем из 2

21 − 11 2 1 + 22 − 12 2 2 + 23 − 13 2 3 = 2 − 1 2

′22 2 + ′23 2	= ′2
2. аналогично 3	= 31 домножаем 1 на ω3 и вычитаем из 3
		11
′32 2 + ′33 2	= ′3
11 1 + 12 2 + 13 3 = 1 − 1
′22 2 + ′23 2		= ′2	− 2′ (2)
′32 2 + ′33 2		= ′3	− 3′

3.′3 = ′32 домножаем 2' на ω’3 и вычитаем из 3'

′22

′22	− ′32′3 2				+ ′23	− ′33′3	3 = ′2 − ′3′3
′′23 3 = ′′2
4. Получаем треугольную систему
11 1 + 12 2 + 13 3 = 1 − 1
′22 2 + ′23 2				= ′2		− 2′
′′23 3 = ′′2						− 3′′
Обратный ход:
5. Из 3'' находим x3; из 2 находим x2; из 1 находим x3.
Пример:
2 1 + 4 2 + 3 3 = 4
3 1 + 2 − 2 3 = −2
4 1 + 11 2	+ 7 3		= 7
1	2	4	3	4
1. 2	3	1	−2		−2
3	4	11	7	7

2.	Исключаем x1											из второго и третьего уравнений и нормируем
			=			1						1	2	1.5	2
		1	2
	2 = 2 − 3 1											0	−5	−6,5	−8
	3 = 3 − 4 1 0 3													1 −1
3.	Исключаем x2											из последнего уравнения
			1									1	2	1.5	2
			=		2							0	1	1,3	1,6
		2			−5
	3 = 3 − 3 2											0	0	−2,9	−5,8
4.	Нормируем
		1									1	2	1,5	2
		=		2							0	1	1,3	1,6
	2		−5
	3	=		3							0	0	1	2
			−2,9
5.	Треугольная система:
	1 + 2 2 + 1,5 3 = 2														1 = 1
		2 + 1,3 2 = 1,6													2 = −1
				3 = 2											3 = 2

Выполняя вручную данные преобразования не трудно ошибиться, поэтому часто используют решение с помощью ЭВМ.

Точность результатов будет определяться точностью выполнения арифметических операций при преобразовании элементов матрицы. Для уменьшения погрешности при делении на диагональный элемент рекомендуют осуществлять такую перестановку уравнений, чтобы поставить на диагональ наибольший по модулю из всех элементов рассматриваемого столбца. Это выбор главного элемента.

= + +1

Тема 13. Метод прогонки.

Модифицированным методом Гаусса является метод прогонки. Он применим для трѐх диагональных матриц.

−1 2 + 1 1 = 1									− 1
−2 3 + 2 2 − 2 1 = 2 − 2											1		1	1	0	0
−3 4 + 3 3 − 3 2 = 3											0 2			2	2	0
				… … … …							0 0 3				3	3
−						=			− 3
				−1
Из 1 выражаем x1
=	1 +		1					=		+				(4)		= 1		= 1
1	1		1	2				1	1 2	1					1	1	1		1
Подставим 4 в 2
−2 3 + 2 2 − 2 1 2 + 1									= 2
Выразим x2											= 2+ 2 1
=	2+ 2 1 +					2										=	2
2	2−1		2		2	−1 2		3			2		2−1 2			2	2−1 2
2 = 2 3			+ 2
=				+				(5)
		+1
Из 3 определяют xn
=		+						(6), при этом x				заменяют по формуле 5
		−1									n-1
	− −1

Затем, зная xn последовательно определяют все xn текущее обратной подстановкой. Последовательность метода прогонки:

1.определяют e1 и f1 из 1;

2.определяют en и fn по

						+
=			=					−1
	− −1					− −1

3.из 3 определяют xn

4.по 5 определяют xn-1, xn-2, …, x1

Формирование коэффициентов новой матрицы (пункты 1-2) – это прямой ход метода прогонки. Определение

неизвестных (пункты 3-4) – обратный ход метода прогонки.

Пример:

−51 1 + 35 2 = 0,2 − 1

15 1 − 51 2 + 35 3 = 0,4 − 2

0 = 0

5 = 1

n=0,…,5

15 2 − 51 3 + 35 4 = 0,6

15 3 − 51 4 + 35 5 = 0,8

Из 1 определяем x1

=

35

− 0,2

= 0,68 − 0,0039

= 0,68

= 0,0039

1

51

2

51

2

1

1

Из 2 определяем x2

=

35

+ 0,4−15 0,0039

= 0,85

− 0,011

= 0,85

= 0,011

51

−15 0,68

2

3

51−15 0,68

3

2

2

… … …

5 = 1

4 = 4 5 + 4

Хотя прямые методы решения СЛАУ весьма эффективны для небольших систем, для больших матриц они уступают итерационным.

Тема 9. Метод релаксации.

Можно увеличить сходимость итерационного процесса в методе Гаусса-Зейделя, если записать итерационную схему в виде+1 − , где а – уточненное значение по методу Гаусса-Зейделя; ω – параметр 0 ≤ ≤

2.

При ω<1 x изменяется медленнее; а при ω>1 быстрее. Однако несмотря на кажущиеся преимущества быстрого изменения x часто поведение неизвестных с увеличением номера итерации носит колебательный характер. Поэтому в ряде случаев для ускорения сходимости решения возникает необходимость «тормозить» значение x, для чего и задают ω<1. В большинстве случаев ω подбирают путѐм численных экспериментов. При ω>1 метод называют последовательной верхней релаксацией, при ω<1 – метод последовательной нижней релаксации, а при ω=0 получают метод Гаусса-Зейделя.

Тема 8. Метод Якоби для СЛАУ.

Любой итерационный процесс начинается с задания по некоторым соображениям начального приближения x1, x2, …, xn. В методе простой итерации каждое новое приближение рассматривается по известным на предыдущем

шаге.
		=		1			− −1					− −1		− −	−1
1				11			1		12		2	13	3	1
		=		1		− −1						− −1		− −	−1
2				22			2		21		1	23	3	2
											… … … … …
				1
	=				−					−1		−	−1	− −		−1
									1		1	2	2	−1		−1
																	− −1
Итерационный процесс заканчивается, когда максимум																						≤ .
Пример:
5 1 − 2 + 2 3 = 8
1 + 4 2 − 3 = −4
1	+ 2 + 4 3 = 4
1	= 0 1 + 0,2 2 − 0,4 3 + 1,6															(0)		= 1,6, (0)			= −1, (0)
2 = −0,25 1								+ 0 2			+ 0,25 3 − 1												= 1
3 = −0,25 1								− 0,25 2 + 0 3 + 1								1			2			3
	(1) = 0,2 ∙ −1										− 0,4 ∙ 1 + 1,6 = 1
		1
(1) = −0,25 ∙ 1,6 + 0,25 ∙ 1 − 1 = −1,15																(1)		= 1, (1)		= −1,15, (1)				= 0,85 – первое приближение x
2																1			2			3
(1)		= −0,25 ∙ 1,6 − 0,25 ∙ −1											+ 1 = 0,85
3
(2)		= 0,2 ∙ −1,15									− 0,4 ∙ 0,85 + 1,6 = 1,03
1
(2) = −0,25 ∙ 1 + 0,25 ∙ 0,85 − 1 = −1,037																(2)		= 1,03, (2)				= −1,037, (2)			= 1,037
2																1				2				3
(2)		= −0,25 ∙ 1 − 0,25 ∙										−1,15 + 1 = 1,037
3
∆ = 0,03								∆	= 0,022			∆	= 0,187					≠
1								2				3

Тема 6. Метод Гауса-Зейделя для решения СЛАУ.

Анализ показывает, что итерационный метод сходится быстрее, если при расчѐте xi на k-итераций в правой части для неизвестных с номерами меньше i подставляют значения неизвестных уже найденные на данной итерации.

	=		1										−				−
1				11							1				12	2		13			3
	=		1										−				−
																			23
2				22							2				21	1					3
	=		1										−				−
																			32
3					33						3				31	1					2
(0)	,	(0)						, (0)
1			2					1			3
(1)		=													−		(0)		−			(0)
1							11						1			12	2				13	3
(1)		=				1									−		(1)		−			(0)
2													2			21	1				23	3
					22 … … … … …
(1)		=				1									−		(1)		−			(1)
3					33								3			31	1				32	2
В общем виде:
( )		=					1						− (−1) − (−1)
1						11							1			12	2					13	3
( )			=					1						− ( ) − (−1)
	2							22							2	21		1			23		3
														… … … … …
( ) =										1					− ( )						− ( )
	3								33						3		31	1				32	2
Пример:
1 = 0,2 2 − 0,4 3 + 1,6																							(0)	= 1,6, (0)	= −1, (0)
2	= −0,25 1 + 0,25 3 − 1																									= 1
3 = −0,25 1 − 0,25 2 + 1																							1	2	3
(1)				= 0,2 ∙ −1												− 0,4 ∙ 1 + 1,6 = 1
	1
(1)				= −0,25 ∙ 1 + 0,25 ∙ 1 − 1 = −1																				1 = 1, 2 = −1, 3 = 1
2
(1)		= −0,25 ∙ 1 − 0,25 ∙																	−1			+ 1 = 1
3

Тема 11. Системы нелинейных уравнений. Методы решения.

Нелинейность в уравнениях системы может возникать из-за использования нелинейных функций и из-за нелинейности коэффициентов системы. Пример: теплофизические характеристики веществ.

			=		2
				2

Для нелинейности систем неизвестны прямые методы решения, а всегда применяются итерационные. В общем

случае нелинейная система уравнений может быть записана как линейная

11 1 + 12 2 + 13 3 + + 1 = 1

21 1 + 22 2 + 23 3 + + 2 = 2 (1)

… + + + + + + + =

1 1 + 2 2 + 3 3 + + == 1, 2, … , (2)

но коэффициенты являются функцией неизвестных величин.

Метод простой итерации для СНАУ.

Для решения 1-2 применяют итерационные методы, в которых на каждой итерации решается линеаризованная система, полученная из исходной нелинейной задачи. На каждом итерационном шаге коэффициенты системы вычисляются по значениям неизвестных, найденных в предыдущем шаге

	=		−1	, −1	, … , −1	(3), а затем эти значения используют для нахождения неизвестных , i=1,…,n
			1	2

путѐм решения линейной системы уравнений. Конец процесса: max | −1 − | ≤ . Метод Ньютона.

Этот подход к решению нелинейных систем более сложен, но позволяет во многих случаях ускорить сходимость итерационого процесса. В основе метода лежит представление всех n-уравнений системы в ряд Тейлора. Разложение в ряд Тейлора:

		+ ∆ ,				+ ∆ , …				=			+ ∆	1	+ ∆	1		+ + ∆				+ + слагаемые более высого порядка
1 1				1 2					2			1	1		2
														1		2
+ ∆ , + ∆ , … , + ∆													= , , … , + ∆										+ + ∆
																			+ ∆					+
1			1 2						2				1 2					1	1	2	2
Если превращение переменных в ∆ таковы, что функция fi																			принимает значения, близкие к корню, то считают,
что левые части этой системы обращаются в нули, ∆2																		и больших степенях отбрасываются, таким образом задача
сводится к нахождению величин ∆ , при которых это происходит.
1 ∆ + 1					∆ + +					1	∆ = − , , … ,
1		1		2		2							1	1	2
							+ + + =
					∆ + +
∆ +										∆ = − , , … ,
	1	1		2		2								1	2
													−1
1		1					1			∆1
										∆2			−2
1		2							×			=		– матрица Якоби.
										∆			−
	1		2

Если точные значения частных производных найти не удаѐтся, то используют их приближѐнные значения, определенные по методу секущих. Искомые приращения ∆ находят из системы уравнений. Метод Ньютона рекомендует находить новые значения неизвестных на k-ой итерации через предыдущее.

( ) = −1 + ∆−1

Если обозначить обратную матрицу Якоби −1 , то тогда метод Ньютона сформулируется

= −1 − −1 −1 −1 (1)

Упрощѐнный метод Ньютона.

Рекомендует брать обратную матрицу Якоби только один раз через нулевое приближение.

= −1 − −1 (0) −1 (2)

При расчѐте по 1 начиная с некоторого момента итерации сходятся быстро по квадратичному закону, а при решении по 2 гарантируется сходимость только по геометрической прогрессии. Счѐт прекращается когда

∆ ≤ .

Для корней xi, имеющих большое значение, это условие может оказаться завышенным. Тогда пользуются

нормируемыми превращениями ∆ ≤ .

Тема 12. Метод возмущения параметров.

Сходимость итерационных методов существенно зависит от удачности начального приближения. Этот метод позволяет получить решение СНАУ вне зависимости от удачного выбора начального приближения.

Суть метода: сначала наряду с функцией

		= 0 (1)	i=1,…,n	j=1,…,n
рассматривается функция
		= 0 (2)	i=1,…,n	j=1,…,n

решение которой известно. Затем деформируя 2, превращают в уравнение 1 с помощью конечного числа n- последовательных малых преращений параметра.

		= −1		+		− −1			K=1,…,N
							1

Решение исходной системы уравнений можно использовать как исходные значения переменных для итерационного решения системы g на первой итерации. Так как эта система мало отличается от предыдущей, то весьма вероятно, что сходимость будет обеспечена. В процессе расчѐта −1 используется для получения решения . В конце счѐта, когда K=N, решаемая система становится эквивалентна исходной. Так как для превращения системы уравнений g, решение которой известно, в решаемую систему f может потребоваться большое количество шагов N, то использование этого метода связано с большими затратами машинного времени. Однако при малой величине шага сходимость на каждом отдельном шаге может быть достигнута всего несколькими итерациями.