метода АА

Рис. 2. Формы продольных колебаний стержня

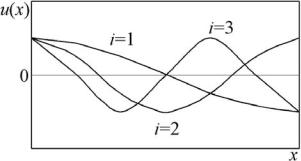
скорости) распространения продольных волн в стержне υ = υф.

Решения уравнения (1) можно представить в виде
ξi(x,t) = ui(x) cos(ω0it + ϕi) ,	(2)

где ui(x) – i-я собственная или амплитудная функция, определяющая форму колебаний (i = 1,2,3…); ω0i – i-я собственная частота, соответствующая ui(x).

Подставим решение (2) в уравнение (1). В этом случае уравнение в частных производных превращается в обыкновенное дифференциальное уравнение для амплитудной функции:

d2u/dx2 + ki

2 u = 0,

(3)

где ki2 = ω0i2/υ2 = ω0i2/υф2. Число ki называется волновым числом. Общее решение уравнения (3) можно представить в виде:

ui(x) = C1cos ki x + C2sin ki x ,

(4)

где С1 и С2 – постоянные интегрирования, зависящие от граничных условий, то есть условий закрепления концов стержня (табл. 1).

Таблица 1. Варианты граничных условий при продольных колебаниях в стержне

Условия закрепления конца стержня	Граничное условие
Конец стержня жестко закреплен	ξ = 0, u = 0
Конец стержня свободен	Fж = ES∂ξ /∂x = 0, ∂ξ /∂x = 0; du/dx = 0

На рис. 2 представлены рассчитанные с помощью (4) амплитудные функции (формы) первых трех мод продольных колебаний i = 1,23 для стержня со свободными концами.

Значения соответствующих собственных частот определяются через волновые числа ki, которые, в сою очередь зависят от размеров и характеристик материала стержня.

Таким образом, решение дифференциального уравнение (3) связано с решением задачи на отыскание собственных функций ui(x) и собственных значений ki2, определяющих характеристики свободных колебаний стержня.

1.2. Изгибные (поперечные) колебания стержней

Жесткость стержня на изгиб обычно меньше, чем на растяжение или кру-

31

чение, поэтому изгибные колебания представляют наибольший практический интерес. При анализе изгибных колебаний используются следующие упрощающие предположения: упругая ось стержня совпадает с линией центров масс поперечных сечений; все точки стержня смещаются только вдоль оси Z, направленной перпендикулярно оси стержня (при этом все поперечные сечения стержня остаются плоскими).

Смещение поперечных сечений стержня вдоль оси Z, (если ось Х располагается вдоль центральной оси стержня), характеризуется функций z(x,t).

При изгибных колебаниях стержня каждому его поперечному сечению dx можно поставить в соответствие изгибающий момент M(x,t), т.е. момент внутренних сил, возникающих в данном поперечном сечении стержня:

M = EJ y ∂2 z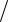∂x2 ,

где Е – модуль упругости материала, Jy – момент инерции сечения относительно оси Y.

Возникновение изгибающего момента сопровождается появлением перерезывающей (поперечной) силы F (x, t), с которой изгибающий момент связан

соотношением ∂M 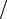∂x = F (x, t).

Если в расчетах учитываются только силы инерции, действующие в направлении оси Z, и силы упругости, препятствующие деформации изгиба, то уравнение движения стержня имеет вид: FЖ = FИ.

В роли силы жесткости Fж выступает перерезывающая сила, приходящаяся на единицу длины стержня: FÆ = ∂F 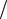∂x = ∂2 M 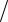∂x 2 .

Сила инерции, приходящаяся на единицу длины: Fи = m0(∂2z/∂t2) . Таким образом, уравнение движения стержня принимает вид

∂2M/∂x2 = m0(∂ 2z/∂t2) или:

	∂2		ΕJ y	∂2 z		+ m0	∂2 z	= 0 .	(5)
	∂x2			∂x2			∂t2

Решения уравнения (5) находятся методом разделения переменных:

zi(x,t) = ui(x) cos(ω0it + ϕi).

(6)

Здесь ui(x) – неизвестные пока амплитудные функции, характеризующие отклонение точек стержня от положения равновесия на резонансных частотах ω0i. Аналогично случаю продольных колебаний стержень при изгибных колебаниях обладает дискретным бесконечным набором резонансных частот.

Функция ui(x) называется также собственной формой колебаний стержня, она зависит от граничных условий и номера собственной формы.

После подстановки (6) в (5) получим

32

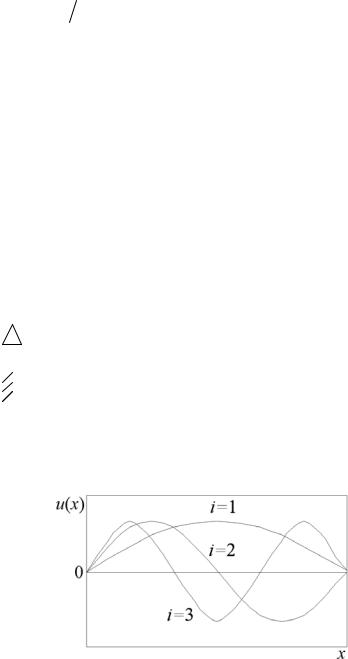
	d 4u		−	m	0	ω	0i		u = 0 .		(7)
	dx 4			EJ y
									(EJ y ) как ki4. Здесь ki – волновое
Произведем замену в (7), обозначив (m0 ω0i )
число с индексом i = 1,2,3,…): ki		4 = (m0ω0i					2)/(EJy) = ρSω0i			2/(EJy), где ρ – плот-
ность материала, S – площадь поперечного сечения стержня. Получим:
(d4u / dx4) – ki								4u = 0 .			(8)
Общее решение уравнения (8) состоит из суммы четырех частных решений:
ui(x) = Aisinkix + Bicoskix + Cishkix + Dichkix .											(9)

Здесь Ai, Bi, Ci, Di – постоянные интегрирования, для определения которых следует рассмотреть условия закрепления концов стержня (табл. 2).

Таблица 2. Варианты граничных условий при изгибных колебаниях стержня

Условия закрепления конца стержня			Схема		Результат
Конец стержня свободно оперт (шар-					Прогиб и изгибающий мо-
					мент равны 0, т.е. u = 0;
нирное крепление)
					u" = 0
					Прогиб и угол поворота се-
Конец стержня жестко закреплен					чения равны 0, т.е. u = 0; u' =
					0
					Изгибающий момент и пе-
Конец стержня свободен					ререзывающая сила равны 0,
					т.е. u" = 0, u''' = 0
На рис. 3 показаны рассчитанные с
помощью (9) амплитудные функции
(формы) первых трех мод поперечных
колебаний стержня, шарнирно закреп-
ленного на обоих концах.
Таким образом, решение диффе-
ренциального уравнение (8) также свя-
зано с решением задачи на отыскание
собственных функций ui(x) и собствен-
ных значений ki2, определяющих харак-			Рис. 3. Формы поперечных колебаний

теристики свободных поперечных колебаний стержня.

33

1.3. Динамические процессы в пластинах

При построении модели, описывающей собственные колебания пластин (рис. 4, а) обычно принимают ряд допущений.

а

б

Рис. 4. Моделирование собственных колебаний пластин:

а– модель пластины; б – результаты численного моделирования колебаний

Кэтим допущения относятся следующие. Изгибные деформации пластины при колебаниях малы по сравнению с ее толщиной, упругие деформации подчиняются закону Гука. Пластина имеет постоянную толщину. В пластине имеется нейтральный слой, который при изгибных колебаниях пластины не подвержен деформации растяжения-сжатия

Для определения резонансных частот, амплитуд и механических напряжений в пластинчатых конструкциях используются различные подходы. Для самых простых частных случаев используется аналитический подход с точным решением задачи. Применяются приближенные методы Рэлея, Ритца и др. Моделирование реальных пластин (например, печатных плат) производится численно с помощью компьютера (рис. 4, б).

Точное решение для определения собственных колебаний пластины основано на принципах, использованных для стержней. В результате уравнение движения пластины можно представить в виде:

∂2 z

∂4 z

∂4 z

∂4 z

m

0

+ D

+ 2

+

= 0.

2

4

2

2

4

∂t

∂x

∂x

∂y

∂y

Здесь m0 – погонная (приведенная) масса пластины (масса единицы площади); z = z(x,y,t) прогиб пластины в направлении оси Z; D = EH3/12(1 – ν2) – цилиндрическая жесткость пластины (свойство жесткости для каждого микроучастка пластины); E – модуль упругости первого рода; Н – толщина пластины; ν – коэффициент Пуассона (обычно ν ≈ 0,25-0,35).

Следует отметить, что пластины тоже обладают бесконечным дискретным набором резонансных частот, значения которых зависят от формы и раз-

34

меров пластин, а также свойств материалов, из которого они изготовлены.

Так же, как и для стержней, определения форм свободных колебаний и соответствующих им резонансных частот, сводится к решению задачи на отыскание собственных функций и собственных значений.

1.4. Задача определения формы потери устойчивости

Помимо прочностного расчета анализ конструкции устройства должен включать исследование вопросов ее устойчивости. Под устойчивостью в данном случае понимается свойство конструкции оказывать сопротивление внешним воздействиям и самостоятельно восстанавливать исходную форму после прекращения силового воздействия.

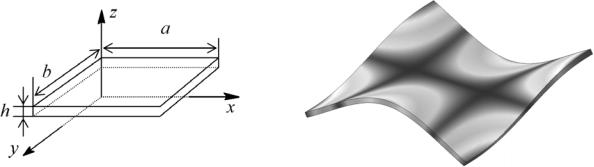
Рассмотрим прямолинейный упругий однородный по длине стержень, к которому вдоль его оси приложена сила F (рис. 5).

Рис. 5. Формы потери устойчивости стержня

При значении силы меньше некоторого критического значения F < Fкр стержень находится в состоянии равновесия и сохраняет первоначально прямолинейную форму. В случае, когда величина силы достигает критической F ≥ Fêð , стержень при малейшем отклонении от продольной оси переходит в

новое равновесное изогнутое состояние. Следует отметить, что статический расчет в данном случае позволил бы определить лишь сжатие стержня вдоль его оси, но не изгиб, то есть форму потери устойчивости.

Анализ формы потери устойчивости конструкции так же, как и для свободных колебаний стержней и пластин приводит к решению задачи определения собственных функций.

35

2. РАСЧЕТ СВОБОДНЫХ КОЛЕБАНИЙ И ФОРМЫ ПОТЕРИ УСТОЙЧИВОСТИ В ПАКЕТЕ SOLIDWORKS

Впакете SolidWorks расчет резонансных колебаний и формы потери устойчивости представлен в соответствующих видах анализа – «Frequency» (Частотный) и «Buckling» (Потеря устойчивости).

Численное моделирование свободных колебаний и формы потери устойчивости так же, как и другие виды расчета, включает задание свойств материала, ограничений и генерацию сетки конечных элементов на геометрии исследуемой конструкции. На полученной сетке формируется массивы данных, представляющих описание задачи.

Впредположении отсутствия изгибных деформаций в элементах конструкции в состоянии покоя уравнение равновесия в матричной форме может быть записано в следующем виде:

[[K ]+ λ[K Ã ]]{W}= 0,

где [K ] и [K Ã ] – глобальные матрицы общей и геометрической жесткости; λ – параметр нагружения; {W} – вектор узловых перемещений ансамбля элементов, соответствующий вектору узловых сил {F}, вызывающих деформацию конечных элементах.

Выбор вида встроенного в SolidWorks решателя – «Direct sparse» (прямой) или «FFEPlus» (итерационный) может определяться видом модели. В случае сложной геометрии конструкции выбор первого из решателей может привести к значительным затратам времени и памяти компьютера.

При интерпретации результатов частотного анализа следует учитывать, что получаемые «эпюры», показывающие форму колебаний носят не более, чем качественный характер. Количественное описание, представленное графическим постпроцессором условно, хотя бы потому, что при расчете свободных колебаний не задается воздействие, вызывающее эти колебания.

3.УКАЗАНИЯ К ВЫПОЛНЕНИЮ РАБОТЫ

1.Подготовьте геометрическую модель исследуемой конструкции.

2.Ознакомьтесь с порядком проведения частотного анализа и расчета формы потери устойчивости в пакете SolidWorks.

3.Выполните частотный анализ и расчета формы потери устойчивости для исследуемой конструкции в пакете SolidWorks.

4.Оформите отчет.

4.СОДЕРЖАНИЕ ОТЧЕТА

1.Цель работы.

2.Краткое описание геометрической модели (включая ее изображение), характеристики материалов, способы закрепления, нагрузки.

36

3.Описание основных этапов расчета (копии экрана – модель сетки и приложенные ограничения/нагрузки).

4.Результатов расчета («эпюры», количественные результаты).

5.Выводы по работе.

5.КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Назовите известные инженерные и научные программы из семейства CAE-пакетов. Дайте их характеристику.

2.Дайте характеристику основных видов ошибок – усечения, округления

ираспространения. Опишите способы их уменьшения.

3.К какой математической задаче сводится задача расчета собственных частот механического резонанса конструкции?

4.Какие виды колебаний рассчитываются в пакете SolidWorks при частотном анализе – свободные и / или вынужденные?

5.Каким образом следует интерпретировать шкалу деформаций при частотном анализе в пакете SolidWorks?

6.Для чего используется расчет формы потери устойчивости?

7.Какими общими свойствами характеризуются частотный анализ и расчет устойчивости формы в пакете SolidWorks?

8.Учитывается ли внутреннее трение при расчете собственных частот механического резонанса конструкции? Если да, то каким образом?

9.Сколько собственных частот по умолчанию обычно рассчитывается в пакете SolidWorks?

10.Существует ли предельное количество собственных частот пластины произвольной формы? Если да, то какое?

11.Чем отличаются результаты расчета деформации детали при статическом нагружении и при анализе формы потери устойчивости?

12.Как изменяется погрешность результата частотного анализа в зависимости от номера моды колебаний? Ответ поясните.

37

ЛАБОРАТОРНАЯ РАБОТА 5 ТЕПЛОВОЙ АНАЛИЗ

Цель работы: изучение методики проведения теплового анализа

впакете SolidWorks.

1.КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Известны три механизма передачи тепла: кондуктивный теплоперенос; конвекция; излучение. Тепловой анализ предназначен для расчета температурного распределения в исследуемом объекте вследствие действия какого-либо из приведенных или всех перечисленных механизмов.

Все три механизма связаны с переносом тепловой энергии из среды с повышенной температурой в область с пониженной температурой. При этом кондуктивный и конвективный перенос тепла требуют наличия некоторой материальной среды, а излучательный механизм – нет.

1.1. Кондуктивный перенос тепла

Кондуктивный теплоперенос – механизм теплопередачи, при котором тепловая энергия переходит от одной точки до другой благодаря взаимодействию между атомами или молекулами среды. Этот механизм наблюдается в твердых веществах, жидкостях и газах.

Кондуктивный теплоперенос не использует общего движения вещества. Теплопроводность газов обусловлена прямыми столкновениями между молекулами, и их теплопроводность низка по сравнению с твердыми веществами, так как они имеют меньшую плотность. Перенос тепловой энергии в жидкостях происходит аналогично газам за исключением того, что ситуация значительно более сложна, так как молекулы более близко расположены, и поля молекулярных сил оказывают сильное влияние на обмен энергии в процессе столкновения. Неметаллические твердые среды передают тепло за счет колебаний решетки, за счет которых передается тепло без переноса вещества. Металлы имеют лучшую теплопроводность по сравнению с неметаллами при нормальных температурах, потому что у них есть свободные электроны, которые переносят тепловую энергию.

Кондуктивный перенос тепла описывается законом Фурье, в соответствии с которым перенос тепла Qcond пропорционален площади S, через которую осуществляется перенос и градиенту температуры dT/dx:

Qcond = – K S (dT/dx) ,

где K – коэффициент теплопроводности, описывающий способность материала передавать тепло. Единицей измерения K является Вт/(м·K). Для плоского слоя, показанного на рис. 1, а формула, описывающая кондуктивный перенос тепла, имеет вид Qcond = – K S ( TH - TC ) / L , где TH – температура в нагретой области

38

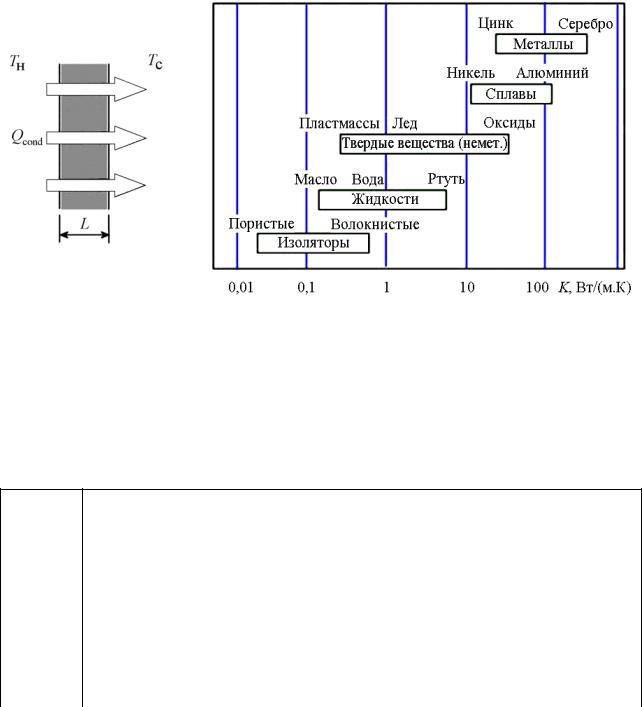
TC – с пониженная температура. На рис. 1, б приведены диапазоны значений теплопроводности различных материалов при комнатной температуре и нормальном атмосферном давлении.

а

б

Рис. 1. Кондуктивный теплоперенос: а – механизм переноса тепла; б – диапазоны значений коэффициента теплопроводности K различных материалов

Для большинства материалов K меняется с температурой. В табл. 1 показано изменение коэффициента теплопроводности K (Вт/(м·K)) от температуры T (K) для ряда материалов.

Таблица 1. Зависимость коэффициента теплопроводности (Вт/м·K) от температуры Температура, K

	Материал
		103	173	273	373	473	573	673	873
	Сталь				15	17	19	21	25
	Свинец	40	37	36	34	33	32	17	20
								(жидк.)	(жидк.)
	Цинк	124	122	122	117	110	106	100	60
									(жидк.)
	Кремний	856	342	168	112	82	66	54	38

1.2. Конвекция

Конвекция – способ передачи тепла, при котором высокая температура передается от твердого тела к соприкасающейся с ним средой (газом или жидкостью), которая за счет ее перемещения отводит тепло от тела. Конвекция включает две составляющих: перенос энергии за счет случайного движения мо-

39

Рис. 2. Циркуляция газа (жидкости) при естественной конвекции

лекул теплоотводящей среды (механизм диффузии), и передачу энергии, связанную с движением макроскопических объемов этой среды.

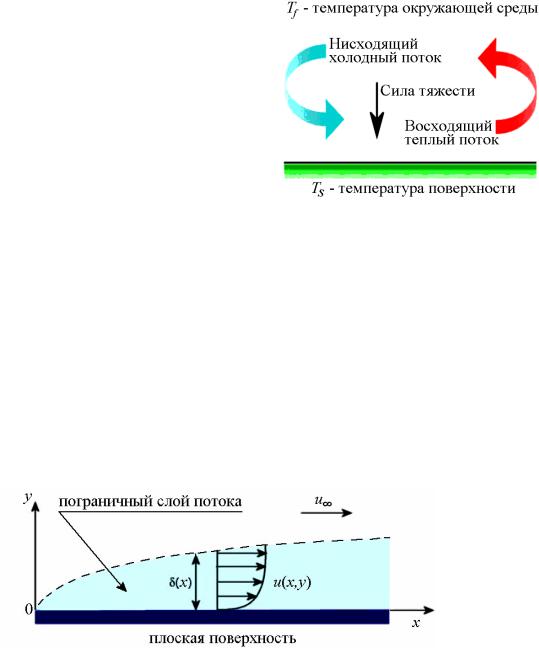
Механизм конвекции можно объяснить следующим образом: поскольку слой среды, соприкасающейся с нагретой поверхностью, становится более теплым, уменьшение ее плотности (при постоянном давлении, плотность уменьшается с ростом температуры) увеличивает ее «плавучесть». Более холодная (более тяжелая) среда опускается к охлаждаемой поверхности, заменяя более теплую. Таким образом, происходит циркуляция газа (жидкости).

Обмен тепла между подвижной средой, имеющей температуру Tf, и поверхностью тела площадью S c температурой TS повинуется закону охлаждения Ньютона, который может быть представлен формулой

Qconvection = h A (TS – Tf) ,

где h – коэффициент конвективной теплоотдачи. Единицей измерения h является Вт/(м2·К). Коэффициент конвективной теплоотдачи h зависит от геометрии системы, характера движения теплоотводящей среды, ее термодинамических и физических свойств.

Характеристики конвективной теплоотдачи определяются процессами в тонком переходном слое газа (жидкости) вблизи охлаждаемой поверхности.

На рис. 3 показано распределение u(x,y) – скорости движения газа (жидкости) воль оси 0x. Вблизи охлаждаемой поверхности скорость потока минимальна, но по мере удаления от поверхности возрастает, достигая максимальной величины в свободном пространстве. Толщина переходного слоя δ(x) определяется положением его верхней границы, на которой скорость u(x,y) составляет 99 % от скорости свободного потока u∞ .

Рис. 3. Распределение скорости газа (жидкости) вблизи охлаждаемой поверхности

Распределение температуры вблизи охлаждаемой поверхности аналогичным образом представлено на рис. 4. Следует заметить, толщина пригранично-

40