метода АА

Министерство образования и науки Российской Федерации Сибирский федеральный университет

КОМПЬЮТЕРНЫЕ ТЕХНОЛОГИИ В НАУКЕ И ПРОИЗВОДСТВЕ

Учебно-методическое пособие для выполнения лабораторных работ

Электронное издание

Красноярск

СФУ

2012

УДК 621.396.6(07)

ББК 32я73

К637

Составитель: А.А. Левицкий

К637 Компьютерные технологии в науке и производстве: учебнометодическое пособие для выполнения лабораторных работ [Электронный ресурс] / cост. А. А. Левицкий. – Электрон. дан. – Красноярск: Сиб. федер. ун-т, 2012. – Систем. требования: PC не ниже класса Pentium I; 128 Mb RAM; Windows 98/XP/7; Adobe Reader V8.0 и выше. – Загл. с экрана.

В учебно-методическом пособии приведены описания лабораторных работ по выполнению компьютерного анализа методом конечных элементов в программе SolidWorks. Изложены краткие теоретические сведения, представлена методика выполнения лабораторных работ.

Предназначено: по кодификатору ГОС ВПО-2 для направлений подготовки магистров 210100.68 – «Электроника и микроэлектроника» и 210200.68 – «Проектирование и технология электронных средств»; по кодификатору ФГОС ВПО-3 для направлений подготовки магистров 210100.68 – «Электроника и наноэлектроника» и 211000.68 – «Конструирование и технология электронных средств». Рекомендуется для всех специальностей и направлений укрупненных групп 210000 «Электронная техника, радиотехника и связь» и 200000 «Приборостроение и оптотехника».

УДК 621.396.6(07)

ББК 32я73

© Сибирский федеральный университет, 2012

Учебное издание

Подготовлено к публикации редакционно-издательским отделом БИК СФУ

Подписано в свет 21.05.2012 г. Заказ 7049. Тиражируется на машиночитаемых носителях.

Редакционно-издательский отдел Библиотечно-издательского комплекса Сибирского федерального университета 660041, г. Красноярск, пр. Свободный, 79

Тел/факс [phone]. E-mail [e-mail] http://rio.sfu-kras.ru

2

ВВЕДЕНИЕ

В настоящих методических указаниях представлены лабораторные работы, целью проведения которых является ознакомление студентов с технологиями численного моделирования конструкций электронных устройств. Лабораторные работы нацелены на выработку навыков, необходимых при решении проектных и научных задач с использованием компьютера.

Лабораторные работы выполняются в среде SolidWorks Simulation (SolidWorks\COSMOSWorks). Расчеты проводятся с использованием базовых возможностей пакета без привлечения специализированных программ анализа, таких как COSMOSFloWorks. Описание настроек приведено для версий 20072011 пакета SolidWorks. В связи с различием вариантов русификации версий пакета названия команд и настроек могут несколько отличаться от приведенных в данных методических указаниях.

Для выполнения работ студенты должны владеть основами работы на персональном компьютере и иметь базовые навыки работы в пакете SolidWorks. Лабораторный практикум проводится каждым студентом индивидуально. Работа выполняется в соответствии с данными методическими указаниями под руководством преподавателя. При выполнении лабораторной работы студент должен предъявить рабочую версию расчета и его результаты на компьютере.

Лабораторная работа считается выполненной после её защиты. Для защиты работы необходимо представить отчёт, оформленный в соответствии с приведенными в данных методических указаниях требованиями.

ЛАБОРАТОРНАЯ РАБОТА 1 РАСЧЕТ РЕАКЦИИ КОНСТРУКЦИИ НА СТАТИЧЕСКУЮ НАГРУЗКУ

Цель работы: изучение методики проведения линейного статического анализа и оценки изделий по критериям прочности в пакете SolidWorks.

1. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

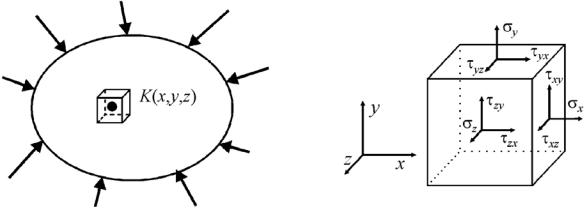
Оценка прочности конструкции электронного устройства является одной из основных задач, решаемых в процессе проектирования электронных устройств. В данной работе рассматривается методика проведения анализа реакции конструкции на статическую нагрузку. Моделирование проводится в рамках линейного описания, при котором справедлив закон Гука, описываемый для одномерного случая (например, при растяжении или сжатии тонкого стержня) выражением σ = Eε, где σ – механическое напряжение, E – модуль продольной упругости (модуль Юнга), ε = l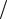L – относительная деформация, l – абсо-

лютная деформация, L – длина деформируемого тела.

3

1.1. Напряженное состояние в точке тела

Рассмотрим некоторое твердое тело, нагруженное поверхностными и распределенными по объему силами – нагрузками. В общем случае распределение внутренних напряжений в объекте неоднородное. Как правило, в некоторых частях тела возникают значительные локальные напряжения. Такие области принято называть концентраторами напряжений. При больших механических напряжениях материала в объекте могут появиться пластические деформации, трещины, с которых начнется его разрушение. Исследование процессов, связанных с потерей прочности конструкций под действием внешних нагрузок представляет значительный практический интерес.

Для анализа напряжений, возникающих в твердом теле, выделим в нем «единичный» куб малого объема (рис. 1), центром которого является некоторая точка K с координатами (x, y, z). Сориентируем ребра куба по осям x, y и z (рис. 2). Будем полагать, что напряженные состояния в малом единичном кубе однородны, одинаковы во всех точках куба. Равнодействующие силы, прило-

женные к площадкам куба называются напряжениями, с единицами измерений

1 H/м2 = 1 Па.

Рис. 1. Единичный куб в твердом теле

Рис. 2. Напряжения на гранях куба

Механические напряжения на каждой из граней разложим на составляющие по трем осям. Нормальные к грани составляющие обозначим буквами σ, а касательные напряжения буквами τ (рис. 2).

Например, к грани, ортогональной координатной оси x, приложено нормальное напряжение σx и два касательных напряжения τxy и τxz, где в индексах на первом месте стоит соответственно x, а на втором – ось, вдоль которой направлена составляющая касательного напряжения. К противоположной грани куба, приложены противоположно направленные нормальное и касательное напряжения, равные по модулю соответствующим напряжениям исходной грани. Положительные направления напряжений соответствуют направлению осей x, y и z. Поэтому, например, если вдоль оси x на куб действует не растягивающая нагрузка то нормальному напряжению σx присваивается положительный знак, а если сжимающая нагрузка – отрицательный.

4

Теоретически можно показать, что для каждой точки K нагруженного тела существует такая система отсчета K(x1, y1, z1) и соответственно такой ориентированный по ее осям «единичный» куб малого объема, для которого все касательные напряжения на его гранях равны нулю. Тогда нормальные к граням куба напряжения называют главными напряжениями в точке тела, а грани соответствующего малого куба, на которые действуют главные напряжения, называются главными площадками в точке К.

Такой «главный» элементарный куб, под действием внешних сил испытывает деформации растяжения-сжатия вдоль направления действия нормальных напряжений. При этом происходит только изменение длин его ребер (в соответствии с законом Гука) без изменения прямых углов между ребрами, поэтому он сохраняет форму прямоугольного параллелепипеда.

Главные напряжения принято отмечать численными индексами: σ1, σ2, и σ3. Порядок расстановки индексов выбирают так, чтобы упорядочить напряжения по убыванию их числовых значений: σ1 > σ2 > σ3 (с учетом знака).

Экспериментальные и теоретические исследования характеристик материалов и способов оценки их прочности привели к созданию ряда критериев прочности (их часто называют теориями). В первую очередь они позволили определить показатели прочности для случаев, когда материал находится в одноосном напряженном состоянии типа растяжение-сжатие, или простейшем плоском напряженном состоянии сдвига при деформации кручения.

В качестве условий прочности полагается, что наибольшее нормальное напряжение для состояния растяжения σTmax или сжатия –σCmin и наибольшее касательное напряжение τmax для деформации кручения не должно превосходить допускаемого напряжения, соответствующего экспериментально установленному пределу текучести (Yield Stress) в случае пластичных материалов или пределу прочности при сжатии или растяжении (Tensile/Compressive Strength) в случае хрупких материалов:

σT max ≤ σT ; σC min ≤ σC или τmax ≤ τLimit ,

где σT = σt 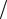n , σC = σc 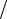n – допускаемые значения нормальных напряжений

при растяжении и сжатии соответственно, связанные с пределом текучести (для пластических материалов), или пределом прочности (для хрупких материалов) коэффициентом запаса прочности n, τLimit – допускаемое касательное напря-

жение.

5

1.2. Критерии прочности

Критерий максимальных нормальных напряжений (Maximum normal stress). Согласно этому критерию предполагается, что предел прочности при сложном напряженном состоянии достигается, когда наибольшее нормальное напряжение σ1 или |σ3| достигает предельного напряжения σT или σC при одноосном напряженном состоянии.

В случае преобладающего влияния σ1 условие имеет вид:

σ1 < σLimit или σ1 / σLimit < 1 ,

где σLimit – предельное напряжение растяжения или сжатия, равное σT или σC. Для плоского напряженного состояния при σ3 = 0 это условие можно за-

писать следующим образом: σС < {σ1, σ2, 0} < σT. На плоскости 0σ1σ2 критерий наибольших нормальных напряжений задает квадратную область. Причем для пластических материалов (с учетом σc ≈ σt) центр области допустимых значений будет находиться в начале координат (рис. 3).

Рис. 3. Критерий максимальных	Рис. 4. Критерий максимальных
нормальных напряжений	касательных напряжений

На практике данный критерий находит подтверждение только для хрупких однородных материалов, таких, как стекло, керамика, инструментальные стали.

Критерий наибольших касательных напряжений (Maximum Shear Stress). Согласно этой теории, известной также как критерий Треска, предельное состояние наступает тогда, когда наибольшее касательное напряжение τmax

достигает опасного значения, то есть при условии τmax ≤ τLimit . Максимальное касательное напряжение связано с максимальным (σ1) и

минимальным (σ3) главными напряжениями соотношением

τmax = (σ1 – σ3) / 2 .

В случае плоского напряженного состояния одно из трех главных напряжений равно нулю. В случае σ3 = 0 область допустимых значений напряжений

6

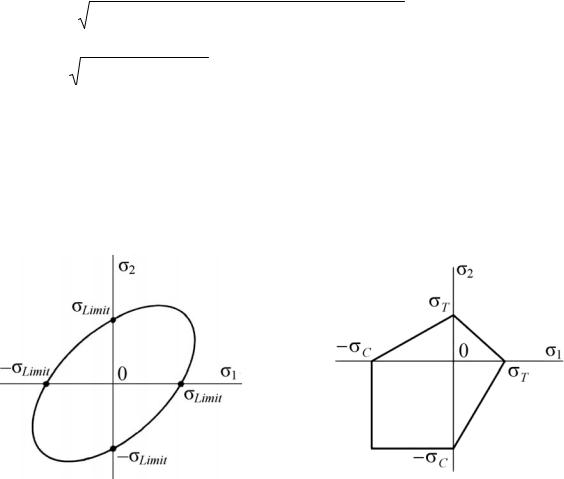
имеет вид, представленный на рис 4.

Критерий Треска дает хорошие результаты для материалов одинаково сопротивляющихся растяжению и сжатию. Аналогом этой теории для материалов, имеющих существенно разные предельные напряжения растяжения и сжатия является критерий Мора-Кулона.

Энергетический критерий Мизеса (von Mises). В соответствии с этим критерием прочность материала при сложном напряженном состоянии обеспечивается, если удельная потенциальная энергия деформации не превосходит допускаемой для одноосного напряженного состояния: W ≤Wmax .

Удельная потенциальная энергия деформации при объемном напряженном состоянии равна

W = [σ12 + σ22 + σ32 − 2v(σ1σ2 + σ2σ3 + σ3σ1 )] 2E ,

где E – модуль упругости (модуль Юнга), v – коэффициент Пуассона. Выражение в квадратных скобках позволяет определить эквивалентное

напряжение σvon Mises, определяющее предельно допустимое напряжение:

σvon Mises < σLimit или

σvon Mises / σLimit < 1 ,

где σ

von Mises

= σ 2

+ σ

2 + σ 2

− 2v(σ σ

2

+ σ

σ

3

+ σ σ ).

1

2

3

1

2

3

1

Для плоского напряженного состояния (σ3 = 0) при v = 0,5 условие при-

нимает вид

σ12 + σ2

2 − σ1σ2

< σLimit

или σ12 +σ2

2 −σ1σ2 < (σLimit )2 . Поэтому

на плоскости 0σ1σ2 это условие определяет эллиптическую область (рис. 5). Недостатком критерия Мизеса, как и критерия Треска, является то, что

они не учитывают различия между растяжением и сжатием и поэтому неприменимы для материалов, имеющих существенно различные характеристики при растяжении и сжатии. Критерий Мизеса применим для пластичных материалов, одинаково сопротивляющихся растяжению и сжатию, к которым относятся большинство металлов, а также некоторые пластмассы.

Рис. 5. Критерий Мизеса

Рис. 6. Критерий Мора-Кулона

7

Критерий Мора-Кулона (Coulomb-Mohr). Этот критерий является обобщением критерия Треска, расширяя его применение на материалы со значительно отличающимися предельными напряжениями сжатия и растяжения. Условие прочности имеет вид:

σ1 − σ3 <1 .

σT σC

Для плоского напряженного состояния одно из трех главных напряжений равно нулю: σ3 = 0, если σ1 и σ2 положительные; или σ1 = 0, если σ2 и σ3 отрицательные. При σ3 = 0 данное условие задает область изменения напряжений, показанную на рис. 6.

Теория Мора-Кулона применяется для хрупких материалов, по-разному сопротивляющихся растяжению и сжатию.

1.3.Общие сведения о методе конечных элементов

Внастоящее время эффективным средством численного моделирования компьютере являются метод конечных разностей и метод конечных элементов. Существуют различные формулировки метода конечных элементов, отличающиеся как в основных, так и в менее значимых деталях. Ограничимся кратким рассмотрением основных этапов решения задачи этим методом.

Формирование сетки. Метод конечных элементов основывается на том, что любое непрерывное распределение физической переменной u(x,y,z,t) в расчетной области, например деформацию или температурное поле, можно аппроксимировать набором кусочно-непрерывных функций, определенных на конечном числе подобластей (конечных элементов). Данные элементы имеют общие узловые точки и в совокупности аппроксимируют форму области.

Взависимости от геометрии и размерности задачи используют различные виды конечных элементов (см. рис. 7). Чаще всего применяются простейшие элементы – симплексы.

а	б	в
Рис. 7. Некоторые	виды	конечных элементов:

a – одномерные; б – двухмерные; в – трехмерные

8

Количество узлов в симплексе на единицу превышает размерность задачи. Для двухмерной задачи симплекс-элементом будет являться прямолинейный трехузловой треугольник, а для трехмерных – прямолинейный четырехузловой тетраэдр. Широкое применение симплексов обусловлено тем, что они позволяют заполнять расчетную область произвольной формы полностью без разрывов, а также на них удобно использовать в качестве аппроксимирующих функций линейные полиномы.

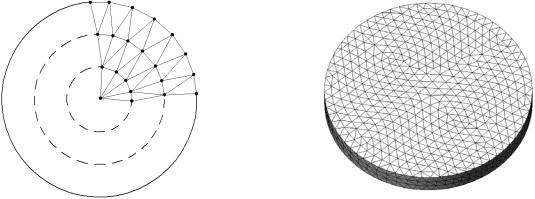
Обычно для разбиения расчетной области на элементы используется специальный алгоритм покрытия, обеспечивающий автоматическую генерацию сетки. Одна из таких процедур работает следующим образом (см. рис. 8, а). Вначале производится нанесение с некоторым шагом узлов на границу области. После этого внутри области строится вспомогательная кривая эквидистантная границе. На кривую также наносятся узлы. Поочередное соединение узлов на первом и втором контурах дает симплексы. Далее все операции повторяются до заполнения симплексами всей области.

Известны и другие алгоритмы формирования конечных элементов, например, «картографический», использующий наложение на расчетную область сетки, которая затем адаптируется к границам и неоднородностям геометрии, или методы, основанные на заполнении объекта набором фигур (тел) с использованием свойств симметрии или отражения.

а

б

Рис. 8. Построение сетки конечных элементов

Пример автоматически сгенерированной трехмерной сетки для круглого диска показан на рис. 8, б.

Конечно-элементная аппроксимация. Рассмотрим построение аппрок-

симации на одномерном примере. Пусть требуется найти распределение некоторой непрерывной функции u(x), вдоль стержня. Распределение u(x) заранее неизвестно, но для удобства иллюстрации метода будем полагать, что его примерный вид соответствует рис. 9, а. На практике эта функция может описывать, например, распределение температуры или деформацию стержня.

Выберем и пронумеруем ряд точек вдоль оси х – это узловые точки (рис.

9

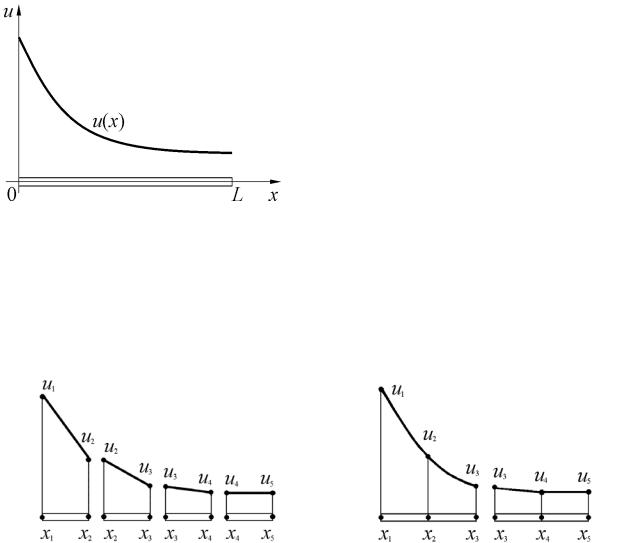
9, б). В нашем примере взято всего пять точек. Вообще говоря, их может быть произвольное количество, и располагаться они могут не на равном расстоянии друг от друга. Обозначим значения u(х) в узловых точках в соответствии с номерами узлов – u1, u2, u3, u4, u5 (см. рис. 9, б).

а

б

Рис. 9. Одномерное распределение

Разбиение расчетной области на конечные элементы может быть проведено различными способами. Можно, например, выделить четыре элемента, включив в каждый из них по два соседних узла (рис. 10, а). А можно выделить в стержне всего два элемента, содержащие по три узла (рис. 10, б).

а

б

Рис. 10. Варианты разбиения стержня на элементы

При использовании четырех элементов, каждый из которых включает только два узла, аппроксимирующая функция в пределах элемента будет линейна по х, так как две точки однозначно определяют прямую линию. Общая аппроксимация зависимости u(х) по всей длине стержня будет складываться из четырех отрезков прямых (рис. 10, а).

Зависимость u(x) в пределах одного элемента, ограниченного двумя соседними узлами xi и xj (j = i + 1), можно представить с помощью линейной интерполяции u(x) ≈ α + αx x. Определив параметры α и αx по известным в точках xi и xj значениям функции ui и uj, запишем функцию элемента следующим образом:

10