метода АА

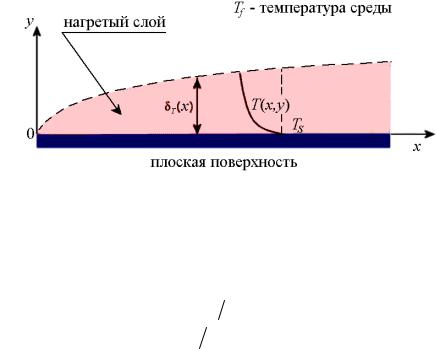
го нагретого слоя δT(x) в общем случае отличается от толщины δ(x) переходного слоя потока газа (жидкости).

Рис. 4. Распределение температуры газа (жидкости) вблизи охлаждаемой поверхности

Относительный вклад скорости потока и теплопроводности в переходном слое характеризуется числом Прандтля, значение которого определяется свойствами охлаждающей среды. Число Прандтля, связывающее δ(x) и δT(x), равно

Pr =	v			η ρ			C p η		,
		=				=
	α		k	(ρC p )			k
где ν – кинематическая вязкость,				α –	коэффициент тепловой					диффузии,
η – коэффициент динамической вязкости;					ρ – плотность среды, k –					теплопро-

водность среды, Cp – теплоемкость среды при постоянном давлении.

Число Прандтля как отношение параметров ν и α характеризует соотношение между интенсивностями молекулярного переноса количества движения и переноса теплоты теплопроводностью – является физической характеристикой среды и зависит только от её термодинамического состояния. Условие Pr = 1 подразумевает одинаковый характер распределений – u(x,y) и T(x,y).

Рассмотрим в качестве основного механизма передачи тепла через переходной слой в направлении оси 0y кондуктивную теплопередачу, через стационарный объем жидкости, приняв поток тепла равным теплопередаче за счет конвекции:

h S (TS – Tf) = – k S (dT/dy)S .

Таким образом, коэффициент конвекции для данной ситуации может быть определен, путем измерения количество переданного тепла и разницы температур TS и Tf (или температурного градиента). Однако, как правило, значения коэффициентов передачи тепла для различных вариантов систем с конвекцией приводятся в справочной литературе.

Вообще, различают два вида конвективной передачи тепла. Естественная конвекция (рис. 5, а). Движение среды (газа или жидкости),

соприкасающейся с твердым телом обусловлено силами плавучести, вынужденными изменениями плотности среды из-за различия температур тела и жид-

41

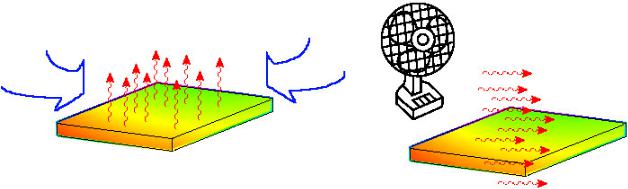
кости. При охлаждении нагретой пластины воздух вблизи ее поверхности становятся более теплыми, что приводит к уменьшению его плотности движению вверх.

Вынужденная конвекция (рис. 5, б). Внешнее средство типа вентилятора или насоса используется, чтобы ускорить поток жидкости вдоль поверхности охлаждаемого тела. Быстрое движение газа или жидкости увеличивает интенсивность отвода тепла.

а

б

Рис. 5. Виды конвективной передачи тепла: а – естественная; б – вынужденная

В табл. 2 приведены некоторые характерные значения для конвективной теплоотдачи.

Таблица 2. Значения коэффициента конвективной теплоотдачи для различных сред

Среда	Коэффициент конвективной теплоотдачи
	h, Вт/(м2·K)
Свободная конвекция газов	5…50
Вынужденная конвекция газов	30…5·102
(воздух/перегретый пар)
Масло – вынужденная конвекция	60…1,8·103
Вода – свободная конвекция	102…103
Вода – вынужденная конвекция	5·102…2·104
Вода – кипение	3·103…6·104
Пленочная конденсация водяных паров	3·103…1,5·104
Капельная конденсация водяных паров	4·104…1,2·105

1.3. Излучение

Тепловое излучение представляет собой тепловую энергию, испускаемую телами в виде электромагнитного излучения вследствие их нагрева. Все тела,

42

имеющие температуру выше абсолютного нуля, излучают тепловую энергию. Свойствами теплового излучения обладает только электромагнитное излучение в диапазоне длин волн 0,4…800 мкм.

Энергия теплового излучения зависит от температуры нагретого тела, его атомной и молекулярной структуры, а также от состояния поверхности тела. Зависимость плотности теплового излучения E (Вт/м2) от температуры тела T описывается законом четвертой степени: E ~ T 4.

Поскольку электромагнитные волны распространяются в вакууме, не требуется какая-либо среда для переноса излучения.

Электромагнитное излучение, включая тепловое излучение, распространяется со скоростью света. В вакууме эта скорость равна c0 = 3·108 м/с, в вещественной среде скорость составляет c = c0/n, где n – коэффициент преломления). Поэтому излучение является самым быстрым из механизмов переноса тепла.

2.ПРОВЕДЕНИЕ ТЕПЛОВОГО АНАЛИЗА В ПАКЕТЕ SOLIDWORKS

Впакете SolidWorks расчет тепловых полей представлен в соответствующем виде анализа – «Thermal» (Тепловой расчет).

Вбазовом варианте тепловой расчет обеспечивает моделирование процессов теплопередачи внутри деталей и сборок, а также между исследуемой конструкцией и окружающей средой. При этом впрямую данный вид расчета не затрагивает моделирование аэрогидродинамических процессов. Решение задач аэро- и гидродинамики обеспечивается специализированными CFD-модулями

(Computational Fluid Dynamics).

Теплопередача в твердом теле описывается уравнением теплопроводно-

сти

∂T

− div(KgradT )= Q

∂T

∂2T

∂2T

∂2T

C

ρ

или C

ρ

= K

+

+

+ Q ,

∂t

∂t

∂ 2

∂

∂

p

p

2

2

x

y

z

где t – время, Q – теплота, выделяемая (поглощаемая) в рассматриваемом объеме. Остальные обозначения соответствуют приведенным выше. Второе уравнение, записанное в прямоугольных координатах соответствует K = const.

Поскольку расчет тепловых полей производится лишь в пределах объема самой конструкции, ее взаимодействие с окружающей средой учитывается только через граничные условия. Внутри конструкции и при контакте деталей доминирующую роль играет кондуктивный перенос тепла. Вклад конвекции и теплового излучения, как правило, менее значим. Конвективные процессы оказывают заметное влияние если они нося вынужденный характер, а излучение становится существенным при большой разнице температуры нагретого тела и окружающей среды (или другого тела, поглощающего излучение).

Описание в пакете SolidWorks параметров кондуктивного (conduction) и конвективного (convection) механизмов переноса тепла соответствует приведенным выше соотношениям. Передачи тепла излучением (radiation) описыва-

43

ется выражением

Qrad = εrad kB S(T f

4 −TS

4 ),

где εrad – излучательная способность, kB – постоянная Больцмана, S – площадь

поверхности, через которую происходит перенос тепла, Tf – температура окружающей среды, TS – температура поверхности тела. Поэтому в пакете SolidWorks для учета данного механизма требуется задать параметры εrad , Tf,, TS.

Площадь S определяется автоматически при выборе поверхности.

В SolidWorks может выполняться как стационарный (Steady State), так и нестационарный (Transient) тепловой расчет. Первый вид расчета дает установившееся распределение температуры в равновесном состоянии. Второй вид анализа показывает процесс перераспределения температуры в конструкции с течением времени. Следует отметить, что при выборе достаточно большого интервала времени нестационарный расчет должен дать распределение температуры соответствующее установившемуся режиму.

Тепловой анализ в SolidWorks позволяет также выполнить статический расчет конструкции с учетом температурных деформаций.

3.УКАЗАНИЯ К ВЫПОЛНЕНИЮ РАБОТЫ

1.Подготовьте геометрическую модель исследуемой конструкции.

2.Ознакомьтесь с порядком проведения теплового анализа в пакете SolidWorks.

3.Выполните расчеты для стационарного и нестационарного режимов.

4.Оформите отчет.

4.СОДЕРЖАНИЕ ОТЧЕТА

1.Цель работы.

2.Краткое описание геометрической модели (включая ее изображение), основные характеристики материалов, граничные и начальные условия.

3.Описание основных этапов расчета (копии экрана – модель сетки и приложенные ограничения/нагрузки).

4.Результаты расчета для стационарного и нестационарного режимов.

5.Выводы по работе.

5.КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Опишите основные механизмы передачи тепла.

2.Поясните физический смысл числа Рейнольдса.

3.Перечислите основные параметры, описывающие модель для теплового расчета (включая свойства материала, виды нагрузок и ограничений).

4.Какие виды сеток используются при тепловом анализе в пакете SolidWorks? Если ограничения на виды сеток существуют, то каковы они?

44

5.Какие основные виды тепловых расчетов обеспечивает тепловой ана-

лиз в пакете SolidWorks?

6.Опишите последовательность расчета при стационарном тепловом анализе в пакете SolidWorks.

7.Опишите последовательность расчета при нестационарном тепловом анализе в пакете SolidWorks.

8.Какие параметры материалов необходимо задавать при проведении теплового анализа?

9.Опишите виды граничных условий (виды нагрузок и ограничений) при тепловом анализе в пакете SolidWorks. Поясните их физический смысл.

10.Как физически интерпретируется при тепловом анализе в пакете SolidWorks отсутствие граничного условия на какой-либо из поверхностей исследуемой модели?

11.Учитывается ли в базовом тепловом анализе в пакете SolidWorks движение окружающей среды – газа или жидкости?

12.Какое из приложений SolidWorks обеспечивает расчет аэрогидродинамических процессов при тепловом анализе?

ЛАБОРАТОРНАЯ РАБОТА 6 ПАРАМЕТРИЧЕСКАЯ ОПТИМИЗАЦИЯ

Цель работы: изучение методики проведения параметрической оптимизации конструкций в пакете SolidWorks.

1. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Под оптимизацией понимают процесс или последовательность операций, позволяющих получить наилучшее в некотором смысле решение среди многих других.

1.1. Задача оптимизации. Основные понятия

Рассматриваемые в задачах оптимизации варианты решения оценивают некоторой характеристикой, которая, может быть выражена численно, например: вес изделия, стоимость и т.п. Довольно часто, чем больше оптимизируемый показатель, тем лучше, например: прибыль предприятия, коэффициент полезного действия устройства, коэффициент усиления усилителя. Однако оптимизация может проводиться и по показателям, которые желательно уменьшать: потребляемая прибором мощность, его размеры, температурный дрейф характеристик. Поэтому параметром задачи, который определяют в первую очередь, является следующий.

Целевая функция – числовой показатель, позволяющий количественно сравнить варианты решения. Целевая функция может изменяться в зависимости

45

от выбираемых разработчиком вариантов реализации проекта, поэтому в задачах оптимизации используют понятие проектных параметров.

Проектные параметры – независимые переменные параметры, которые полностью и однозначно определяют решаемую задачу проектирования. В качестве проектных параметров в зависимости от вида решаемой задачи могут выступать различные величины: размеры элементов конструкции, масса изделия, сопротивления резисторов в электрической схеме, характеристики материалов, концентрация химических веществ и т.п.

Количество проектных параметров характеризует степень сложности задачи оптимизации. Обозначив целевую функцию буквой F, а проектные параметры через x с соответствующими индексами, запишем целевую функцию как зависимость:

F = F(x1,x2,x3,...,xn) .

Здесь n – число проектных параметров, определяющее размерность задачи. Как правило, задачи оптимизации рассматриваются применительно к

случаю поиска минимума функции, поэтому в дальнейшем ограничимся рассмотрением задач минимизации. Задача поиска максимума целевой функции F(x1,x2,...,xn) равносильна задаче минимизации, только с отрицательной функ-

цией –F (x1,x2,...,xn).

Пространство проектирования – область, определяемая проектными параметрами. Пространство проектирования обычно ограничено рядом условий, связанных с сущностью задачи.

Выделяют два типа задач оптимизации – безусловные и условные. Условные задачи оптимизации или задачи с ограничениями отличаются от безусловных задач наличием некоторых дополнительных условий (ограничений), которые необходимо учитывать при поиске решения. Различают два вида ограничений ограничения-равенства и ограничения-неравенства.

Ограничения-равенства выражают зависимость между проектными параметрами, которые должны учитываться при отыскании решения. Эти ограничения можно записать в виде

f1(x1, x2 , x3 ,K, xn )= 0, f2 (x1, x2 , x3 ,K, xn )= 0,

KKKKKKKKKK fm (x1, x2 , x3 ,K, xn )= 0.

Так, например, процентные доли составляющих в некоторой смеси, рас-

n

творе (переменные x1,x2,...,xn) должны удовлетворять условию ∑xi =100, то

i=1

есть их сумма должна быть равна 100 %. Другой пример – сопротивления резисторов в делителе напряжения должны всегда находиться в заданном отношении.

46

Рис. 1. Одномерная целевая функция

В некоторых случаях из этих соотношений часть проектных параметров можно выразить через другие. Тогда эти переменные можно исключить из процесса оптимизации, что позволяет уменьшить размерность задачи и облегчить ее решение.

Ограничения-неравенства – этот вид ограничений выражается неравенствами, имеющими вид

a1 ≤ ϕ1 (x1 , x2 , x3 ,K, xn )≤ b1 , a2 ≤ ϕ2 (x1 , x2 , x3 ,K, xn )≤ b2 ,

KKKKKKKKKKKK ak ≤ ϕk (x1 , x2 , x3 ,K, xn )≤ bk .

На практике ограничения могут настолько сильно ограничивать область допустимых значений проектные параметров, что наилучшее решение будет соответствовать одной из границ области проектирования, либо задача не будет иметь ни одного удовлетворительного решения. Поэтому в большом числе случаев приходится довольствоваться улучшением известных решений, а не доведением их до совершенства.

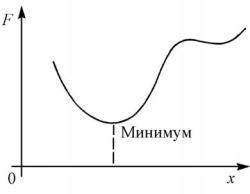
Целевая функция может зависеть от одного, двух и более проектных параметров. Если в задаче только один проектный параметр, целевую функцию изображают графиком на плоскости (рис. 1).

В случае, когда параметров два, целевую функцию можно представить поверхностью в пространстве трех измерений (рис. 2, а) или линиями постоянных значений целевой функции F(х1,х2) = const в системе координат х1, х2 (рис. 2, б). При трех и более проектных параметрах целевые функции описываются гиперповерхностями, которые не поддаются изображению обычными средствами.

Целевая функция и проектные параметры могут иметь особенности, определяемые

спецификой решаемой задачи. Целевую функцию, например, не всегда удается выразить в замкнутой математической форме, иногда ее зависимость от проектных параметров может быть представлена в табличном виде. Проектные параметры в некоторых случаях также принимают только целые значения. Таким примером может служить количество выступов на радиаторе охлаждения или число винтов крепления детали в конструкции.

47

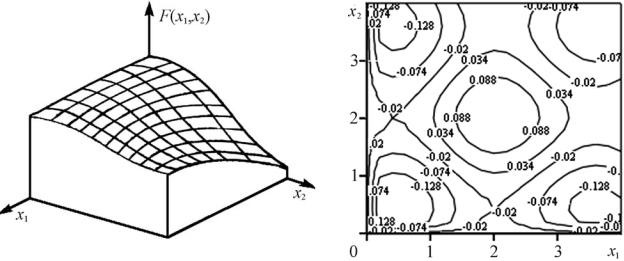
а

б

Рис. 2. Двумерная целевая функция, виды отображения: а – поверхностью; б – линиями постоянных значений

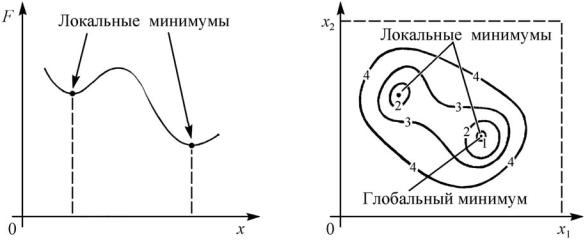
Сложность решения задачи оптимизации зависит от принадлежности задачи к классу одноэкстремальных (унимодальных) или много экстремальных (мулътимодальных). Такая классификация связана с существованием минимумов двух типов – локальных и глобальных.

Локальный оптимум – точка пространства проектирования, в которой целевая функция имеет экстремальное значение (минимум или максимум) по сравнению с ее значениями во всех других точках ее ближайшей окрестности.

Глобальный оптимум – это экстремальное значение целевой функции на всем пространстве проектирования. Данное значение лучше всех других экстремумов, соответствующих локальным оптимумам, и именно его ищет конструктор.

Локальных минимумов в задаче может быть больше одного, а иногда очень много. Возможен случай нескольких равных глобальных оптимумов, расположенных в разных частях пространства проектирования. В этих случаях задача является многоэкстремальной и приходится вести поиск наилучшего решения среди ряда локальных оптимумов.

На рис. 3. показаны примеры одномерной и двумерной целевых функций, имеющих два локальных оптимума. Для того, чтобы не принять за оптимальное решение задачи первый из найденных локальных оптимумов, используют новый запуск процедуры поиска оптимума из разных точек пространства проектирования.

На практике в процессе оптимизации стремятся улучшить не один, а несколько показателей, среди которых обычно рассматривают себестоимость, степень надежности, геометрические размеры, потребляемая мощность и другие. Любой из этих критериев пригоден как критерий оптимизации. Такая задача является многокритериальной, и в ней можно использовать векторную целевую функцию FV(X) = (F1(X), F2(X),...,FS(X)), состоящую из s компонентов.

48

Здесь X – набор параметров проектирования: X ≡ (x1 , x2 ,K, xn ).

а

б

Рис. 3. Примеры целевых функций, имеющих два локальных оптимума: а – одномерной; б – двумерной

Идеальным решением была бы такая точка X в пространстве проектирования, чтобы все критерии Fi одновременно были оптимальными. К сожалению, обычно, используемые критерии противоречивы. Как правило, конструкция изделия не может быть одновременно самого высокого качества и самой дешевой.

В таких случаях разработчик должен ввести систему приоритетов и поставить в соответствие каждой целевой функции Fi некоторый безразмерный весовой коэффициент. В результате векторная функция FV(X) становится «функцией компромисса», позволяющей в процессе оптимизации пользоваться одной составной целевой функцией. Применение функции компромисса позволяет включить в нее и «штрафные функции», которые могут, например, «ухудшать» FV(X), если алгоритм поиска оптимума пытается выйти за пределы области допустимых значений проектных параметров.

1.2. Одномерная оптимизация

На примере одномерной задачи оптимизации (когда имеется только один проектный параметр x) рассмотрим локальные методы поиска (методы прямого поиска) экстремума. Эти методы основаны на сравнении значений целевой функции в некоторых точках X1, X2, …, которые иногда называют точками испытаний. В зависимости от алгоритма выбора этих точек различают ряд локальных методов поиска.

Задачу одномерной оптимизации поставим следующим образом. Значение проектного параметра x, соответствующее экстремуму целевой функции будем искать на отрезке a ≤ x ≤ b. При этом будем предполагать, что исследуемая целевая функция является «унимодальной», то есть имеет в рассматриваемом интервале только один оптимум. Интервал значений x, в котором находит-

49

ся оптимум, будем называть «интервалом неопределенности».

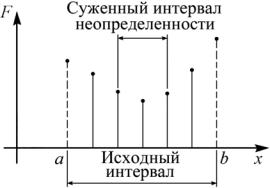
Наиболее естественным представляется сравнение целевой функции в точках испытаний, расположенных на равном расстоянии внутри исследуемого отрезка. В этом случае поиск минимума функции можно сравнить с поиском в водоеме самого глубокого места, когда проводят последовательные замеры глубины. Если в ходе замеров сначала глубина увеличивалась, а затем начала уменьшаться, значит, ее пиковое значение пройдено и интервал неопределенности можно сузить до границ двух последних шагов. Графическая иллюстрация такого варианта поиска минимума функции, называемого пошаговым поиском или методом перебора, показана на рис. 4.

Оценим коэффициент сужения интервала неопределенности K. Разделив исходный отрезок [a, b] на N частей, с помощью N+1 точек, тогда K = 2 / (N + 1). Для того чтобы сузить исходный интервал неопределенности в сто раз, то есть получить значение K = 0,01, требуется вычислить целевую функцию в 199 точках, а при

K = 0,001 и N = 1999. Рис. 4. Метод пошагового поиска

Понятно, что эффективность этого подхода при необходимости существенного уменьшении интервала неопределенности быстро падает. Поэтому можно модифицировать метод, производя поэтапное сужение интервала. Например, для получения K = 0,01, на первом этапе вычислить функцию в 19 точках и получить сначала K1 = 0,1, а затем, вычислив на сокращенном интервале неопределенности еще 19 значений функции, получить K = 0,01. При этом необходимо сделать всего 38, а не 199 вычислений. В общем случае коэффициент

сужения интервала неопределенности при N ≥ 3 составляет K = 22 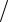(N −1).

Логическим развитием описанного метода является метод поиска оптимума делением отрезка пополам. В этом методе интервал неопределенности делится на каждом этапе на две равных части. Следует отметить, что значение целевой функции в середине каждого нового интервала, полученного после сужения, уже известно. Поэтому на следующем этапе требуется вычислить только два (вместо трех) значения целевой функции.

Известны и другие методы одномерного поиска, в частности, метод дихотомии, золотого сечения, Фибоначчи.

1.3. Методы многомерного поиска

При решении многомерных задач оптимизации прямые методы поиска, рассмотренные выше, малоэффективны. Это объясняется тем, что объем вычислений, необходимых для сужения интервала неопределенности в многомер-

50