
- •В.В. Черепанов, Н.С. Бакшаева
- •Киров 2004
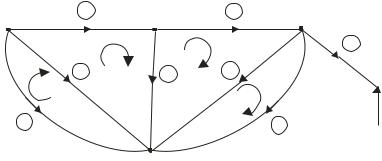
- •Рис.2.1. Классификация методов расчета установившихся режимов.
- •Здесь матрица
- •Вариант №1
- •Вариант №2
- •Вариант №3
- •Вариант №4
- •Вариант №5
- •Вариант №6
- •Вариант №7
- •Вариант №8
- •Вариант №9
- •Вариант №10
- •Вариант №1
- •Вариант №2
- •Вариант №3
- •Вариант №4
- •Вариант №5
- •Вариант №6
- •Вариант №7
- •Вариант №8
- •Вариант №9
- •Вариант №10
- •“Прикладные математические методы ч.1”
- •Литература
- •Оглавление
В.В. Черепанов, Н.С. Бакшаева
МАТРИЧНЫЕ МЕТОДЫ РАСЧЕТА РЕЖИМОВ ЭЛЕКТРИЧЕСКИХ СЕТЕЙ
Учебное пособие
|
1 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[M][I] = [J] |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
3 |
& |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||
|
|
& |
Ιу2 |
[ |
|
][ |
в |
] |
[ |
|
][ |
] |
||
|
|
|
3 |
|
|
|||||||||
4 |
|
Ιу1 |
|
& |
|
N |
U |
|
= N |
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ιу3 |
|
|
|
|
|
|
|
|
|
|
Киров 2004
УДК 621.311.1
В.В. Черепанов, Н.С. Бакшаева. Матричные методы расчета режимов электрических сетей. – Киров.
Учебное пособие предназначено для студентов, обучающихся по специальностям 100400 “Электроснабжение” и 181300 “Электрооборудование и электрохозяйство предприятий, организаций и учреждений”. Рекомендуется при изучении дисциплины “Прикладные математические методы в энергетике”.
Впособии описывается применение алгебры матриц и теории графов
красчету установившихся режимов электрических сетей. Для студентов заочного отделения приведены задания к контрольной работе и методические указания по их выполнению.
Учебное пособие подготовлено на кафедре электроснабжения Вятского государственного университета.
Рецензент: заведующий кафедрой электроснабжения Московского энергетического института, доктор технических наук, профессор С.И. Гамазин.
2
Введение
Задачей электроснабжения является бесперебойное обеспечение потребителей электроэнергией требуемого качества. Эта задача выполняется с помощью систем электроснабжения.
Проектирование и эксплуатация систем электроснабжения требуют расчета их режимов работы. На стадии проектирования расчет режимов систем необходим для выбора их элементов, а на стадии эксплуатации– для принятия мер к повышению экономичности их работы, то есть оптимизации режимов.
При расчетах режимов(состояний) систем электроснабжения составляются схемы замещения систем, которые представляют собой совокупности реактивных и активных сопротивлений, замещающих их элементы. При наличии схемы замещения расчет режима сводится к обычному, известному из курса теоретических основ электротехники, расчету электрических цепей. Однако при анализе режимов систем электроснабжения инженеру приходится иметь дело со сложными электрическими цепями. Достаточно сказать, что схемы замещения современных систем электроснабжения могут иметь десятки узлов и сотни ветвей, а параметры режима систем непрерывно изменяются во времени, причем часть из них изменяется случайным образом. Все это во многих случаях не позволяет использовать при расчетах привычные приемы ручного счета.
Поэтому в настоящее время разработаны и продолжают разрабатываться специальные математические методы расчета и оптимизации режимов систем электроснабжения. Причем использование этих методов вследствие их трудоемкости возможно, как правило, только при применении ЭВМ. К числу
таких методов следует отнести в первую очередь метод топологического анализа и методы теории вероятностей.
В настоящем пособии описаны матричные методы расчета режимов систем электроснабжения. Изложение материала в пособии предполагает знание курсов математики, теоретических основ электротехники, электрических измерений и электрических систем и сетей.
3
1. Основы применения алгебры матриц к расчету режимов электрических сетей.
1.1. Общая характеристика проблемы.
Проектирование и эксплуатация СЭС предприятия требуют расчета режима ее работы. Под режимом СЭС понимают ее состояние в любой момент времени или в некоторый промежуток времени. На стадии проектирования расчет режимов СЭС необходим для выбора их элементов, а на стадии эксплуатации – для принятия мер к повышению экономичности их работы.
При расчетах режимов(состояний) систем электроснабжения составляются схемы замещения систем, которые представляют собой совокупности реактивных и активных сопротивлений, отражающие свойства всех участков СЭС с необходимой для поставленной задачи степенью полноты. При наличии схемы замещения расчет режима сводится к обычному, известному из курса теоретических основ электротехники, расчету электрических цепей.
Режим всякой линейной электрической цепи, представляющей в схеме замещения электрическую сеть, определяется системой линейных алгебраических уравнений. Их число соответствует числу независимых узлов или независимых контуров, образованных электрической сетью. Схемы замещения современных электрических сетей могут содержать десятки и сотни независимых узлов. Поэтому для определения режима сети приходится решать системы, содержащие большое число уравнений. Непосредственное совместное рассмотрение уравнений оказывается настолько громоздким, что их решение практически невозможно без применения вычислительных машин.
Одним из эффективных способов облегчения расчетов и сокращения требуемого для этого времени является применение методов матричной -ал гебры. Матричные методы расчета режимов сетей не открывают каких-то принципиально новых возможностей для решения электрических задач. Они лишь обеспечивают удобную и легко приспособляемую к технике расчета на ЭВМ форму записи. С их помощью можно решить такие задачи, которые изза их сложности решить иным путем было бы практически невозможно. Именно в этом и состоит главное преимущество матричных методов для инженера, рассчитывающего электрические сети.
Алгебра матриц оперирует не с отдельными величинами, входящими в систему уравнений, а с группами величин, обладающими общими признаками. При этом группа из большого числа величин может быть обозначена одним символом. Алгебраические действия с символами похожи на обычные действия, известные из элементарной алгебры. Учитывать приходится лишь некоторые ограничения и особенности. Алгебра матриц упрощает запись
4
весьма сложных по техническому выполнению операций и не отвлекает внимание инженера от решения основной задачи.
Применение элементов теории графов позволяет получить обобщенные представления о схеме замещения системы электроснабжения независимо от ее фактического вида, сложности и параметров. Это дает возможность выполнить в общем виде исследования, применимые практически к любым схемам замещения. При этом упрощается и графическое представление схем. Основоположником применения теории графов к электрическим схемам является Кирхгоф, который спустя два года после опубликования знаменитых законов для токов и напряжений сформулировал основные топологические правила решения контурных уравнений схемы. Он впервые показал связь функций электрической схемы с ее геометрией.
Сочетание преимущества аналитического представления схем замещения в теории графов с символическими приемами записи систем линейных алгебраических уравнений в алгебре матриц привело к широкому использованию матричного метода для определения режимов электрических сетей. Для простых сетей применение матричных методов не оправдано. Применять их рекомендуется только для анализа режимов сложных сетей.
1.2. Некоторые сведения из теории матриц.
Основные определения и соотношения. Матрицей называется таб-
лица величин, расположенных (записанных) в определенной последовательности. Каждая из величин, входящих в матрицу, называется элементом матрицы. Запись группы величин в виде матрицы не предусматривает выполнение каких-либо действий над ними. Это лишь форма упорядоченной записи данных величин в виде условной таблицы.
Элементы матрицы могут быть записаны в виде одного столбца:
éа1 ù êêа2 úú
[A ]= а[i =]êê . úú. ê . ú
ê . ú
ê ú êëаn úû
Такая матрица называется столбцовой или матрицей-столбцом.
Матрица, состоящая из одной строки, называется строчной или матри- цей-строкой и обозначается следующим образом:
[аi ]=[a1,a2 ...an ] .
5
Матрица, имеющая по нескольку строк
угольной:
|
|
éа11 |
а12 ... |
éа |
ù |
ê |
а22 ... |
=êа21 |
|||
ë |
ij û |
ê ... |
... ... |
|
|
ê |
an2 ... |
|
|
ëаn1 |
и столбцов, называется прямо-
а1m ù
а2m ú
ú
... ú
ú
anm û
В этой матрице первый индекс элемента означает номер строки, а второй - номер столбца, в котором он расположен.
Если число строк матрицы равно числу ее столбцов, матрица на-
зывается квадратной.
Элементы а11, а22 … аnn, находящиеся на пересечении строк и столбцов, отмеченных одинаковыми номерами, считаются расположенными на главной диагонали матрицы.
Если элементы квадратной матрицы, расположенные симметрично относительно главной диагонали, одинаковы (аij = аji), то такая матрица называется симметричной. Если все элементы матрицы, кроме диагональных,
равны нулю – |
|
|
|
|
|
|
|
|
|
éa11 |
0 ... |
0 |
ù |
|
|
éа |
ù |
ê |
0 |
a22 ... |
0 |
ú |
, |
= ê |
|
... ... |
... |
ú |
|||
ë |
ij û |
ê ... |
ú |
|
|||
|
|
ê |
0 |
0 ... |
|
ú |
|
|
|
ë |
ann û |
|
|||
то матрица называется диагональной, а если каждый элемент главной диагонали такой матрицы равен единице –
é1 |
0 ... |
0 ù |
||
ê |
0 |
1 ... |
0 |
ú |
[1 ]= ê |
ú |
|||
ê... |
... ... |
...ú |
||
ê |
0 |
0 ... |
1 |
ú |
ë |
û |
|||
то матрица называется единичной.
В электротехнике, кроме того, находят применение единичные матри-
цы[n]и[nt ]:
6
é1ù |
|
ê ú |
|
ê1ú |
[nt ]=[1 1 . . . 1] . |
[n ]= ê.ú , |
|
ê ú |
|
ê.ú |
|
ê ú |
|
ë1û |
|
Если каждый элемент матрицы равен нулю, то матрица является нуле-
вой.
Транспонированной матрицей [At ] для матрицы [A] размера m×n
называется матрица размера n ×m, получаемая из матрицы [A]заменой ее строк столбцами, т.е. если
|
|
|
|
é a11 |
|
|
|
|
|
ê |
|
é |
ù |
= |
êa21 |
||
[A ]=ëаij û |
ê ... |
||||
|
|
|
|
ê |
|
то транспонированная матрица |
|
|
ëam1 |
||
|
|
|
|
||
|
|
|
|
|
éa11 |
|
é |
ù |
|
|
ê |
[At =] |
= |
êa12 |
|||
ëa ji |
û |
ê ... |
|||
|
|
|
|
|
|
ê
ëa1n
a12 |
... |
a1n |
ù |
|
a22 |
... |
a2n |
ú |
|
ú |
, |
|||
... |
... |
... |
ú |
|
am2 |
... |
|
ú |
|
amn û |
|
|||
a21 |
... |
am1 |
ù |
a22 |
... |
am2 |
ú |
ú . |
|||
... |
... |
... |
ú |
a2n |
... |
|
ú |
amn û |
|||
Алгебраические операции над матрицами. Сложением двух матриц называется операция, при которой складываются их элементы, расположенные на одинаковых местах.
[ |
|
] [ ] |
[ |
|
éa11 |
a12 |
... |
a1m ù |
éb11 |
b12 |
... |
b1m |
ù |
|||||||||||
C |
= |
ê] |
|
... |
... |
|
... |
ú |
ê |
|
... |
... |
... |
ú |
||||||||||
|
= A + B |
|
ê ... |
|
ú |
+ ê ... |
ú = |
|||||||||||||||||
|
|
|
|
|
êa |
n1 |
a |
n2 |
... |
a |
nm |
ú |
êb |
n1 |
b |
n2 |
... |
b |
|
ú |
||||
|
|
|
|
|
ë |
|
|
|
|
|
û |
ë |
|
|
|
nm û |
||||||||
|
|
|
|
|
éa11 + b11 |
a12 + b12 |
|
. . . a1m + b1m ù |
|
|
|
|||||||||||||
|
|
|
= |
ê |
|
|
|
|
|
. . . |
|
|
. . . |
|
|
|
. . . |
ú |
|
|
|
|||
|
|
|
ê . . . |
|
|
|
|
|
|
|
|
ú |
|
|
|
|||||||||
|
|
|
|
|
êa |
|
+ b |
|
|
a |
|
+ b |
|
|
. . . a |
|
|
+b |
. |
|
|
|
||
|
|
|
|
|
n1 |
n1 |
n2 |
n2 |
nm |
ú |
|
|
|
|||||||||||
|
|
|
|
|
ë |
|
|
|
|
|
|
|
nm û |
|
|
|
||||||||
Матрицы-слагаемые должны иметь одинаковое количество соответственно строк и столбцов.
7
Операция вычитания матриц выполняется аналогично операции сложения, т.к. может рассматриваться как операция сложения с обратным знаком .
При сложении и вычитании матриц справедливы переместительное и сочетательное свойства:
[A]±[B]=[B]±[A];
и[A]±[B]±[С]=[A]±([B]±[С])=([A]±[B])±[С].
Если[A]+[B]=[С], то[At ]+[Bt ]=[Ct ] , где индексом t отмечены соответству-
ющие транспонированные матрицы.
Умножением двух матриц называется такое действие, при котором в качестве элементов, расположенных на пересечении i-й строки и j-го столбца матрицы-произведения, принимаются суммы попарных произведений элементов, расположенных на одинаковых местах указанных строк матрицымножимого и столбцов матрицы-множителя:
|
C |
= A B = |
éa |
|
a |
|
|
a |
|
ù |
éb11 |
b12 ù |
|
|
|
|
|
|||||||||
[ |
ê] |
11 |
12 |
|
13 |
ú |
êb |
21 |
b |
|
ú = |
|
|
|
|
|||||||||||
|
] [ |
][ |
|
|
|
|
|
|
a |
|
ê |
|
|
22 |
ú |
|
|
|
|
|
||||||
|
|
|
|
|
ëa21 a22 |
|
23 û |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
b32 |
ú |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ëb31 |
û |
|
|
|
|
|
|||||
|
é a11b11 +a12b21 +a13b31 |
|
a11b12 +a12b22 +a13b32 ù |
|||||||||||||||||||||||
= êa b +a |
22 |
b |
21 |
+a |
23 |
b |
31 |
|
a b +a |
22 |
b |
22 |
+a |
23 |
b |
32 |
ú. |
|||||||||
|
ë |
21 |
11 |
|
|
|
|
|
21 |
12 |
|
|
|
û |
||||||||||||
Число строк матрицы-множителя должно быть равно числу столбцов матрицы-множимого. В общем случае операция умножения матриц не обла-
дает переместительным свойством, т.е.
[A]×[B]¹[B]×[A].
Поэтому |
следует |
различать |
умножение |
матрицы[A]на |
цу[B] слева [B] [A] |
и справа [A] [B] . Для диагональных матриц перемести- |
|||
тельное свойство справедливо.
Сочетательное и распределительное свойства справедливы во всех случаях умножения матриц:
[A][B][C]=([A][B])[C]=[A]([B][C]); [A]([B] ±[С])=[A][B] ± [A][С].
Постоянный множитель р для всех элементов матрицы можно вынести за знак матрицы:
8
р[A]=éëраij ùû,(i =1,..., n; j =1,..., m).
Умножение любой матрицы [A]на единичную справа или слева не
приводит к ее изменению.
[A][1]=[1][A]=[A].
Умножение любой матрицы на нулевую приводит к нулевой матрице.
[A][0]=[0][A]=[0].
Понятие обратная матрица возникает при решении матричных уравнений. Оно в известной мере заменяет операцию деления, которая в непосредственном виде в алгебре матриц отсутствует.
Квадратные матрицы одинакового порядка, произведение которых дает единичную матрицу, называются взаимно обратными или, сокращенно, об-
ратными.
[A ]éëA-1ùû =[1].
Обратная матрица отмечается показателем степени"-1". Прямоугольные матрицы обратных не имеют.
Обратная матрица состоит из элементов, которые определяются путем решения системы линейных алгебраических уравнений:
aij-1 =D-1M ji (-1 ()i+ j) ,
где D - определитель матрицы [А] ; Mji - минор для элемента аji матрицы [A], т.е. определитель матрицы на единицу меньшего порядка, полученной из матрицы [A] путем исключения строки j и cтолбца i.
Определение обратной матрицы может иметь место только в случаях, когда определитель исходной матрицы отличен от нуля. Такие матрицы называют неособенными. Квадратные матрицы, определитель которых равен нулю, называются особенными и обратных матриц не имеют. К ним относятся нулевая матрица, а также такая матрица [А], суммы элементов которой по
всем строкам и по всем столбцам равны нулю:
[nt ][A]= [0], [A][n]=[0].
Кроме того, особенной является матрица, в которой все элементы одной из строк или одного из столбцов равны нулю.
1.3. Схема замещения системы электроснабжения.
Анализ работы системы электроснабжения требует расчета ее режимов, т.е. определения параметров режима. Такие расчеты выполняются при помощи схем замещения сети, элементы которых отражают свойства всех ее участков. При этом схема замещения может отличаться от принципиальной
9
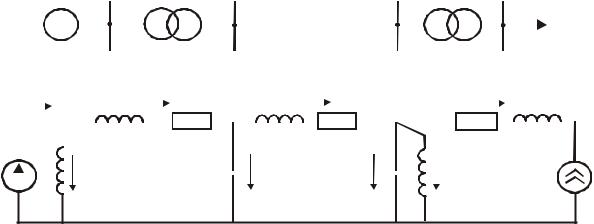
схемы соединений звеньев электрической цепи. Чаще всего приходится рассматривать симметричные режимы трехфазных сетей. Схема замещения в этих случаях составляется на одну фазу и имеет нейтраль. На рис.1.1 показаны схема электроснабжения и схема ее замещения
|
|
Г |
1 |
|
|
|
Т1 |
2 |
|
|
|
ЛЭП |
|
3 |
|
|
|
Т2 |
|
|
4 |
|
|
|
|
|||||||||||||
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
& |
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Ι |
|
|
|
|
|
|
Ι2 |
|
|
|
|
|
|
|
Ι3 |
|
|
|
|
|
|
|
|
|
|
Ι4 |
|
|
|
|
|
|
|||||
1 |
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
4 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
& |
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
& |
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
Ι |
|
|
|
|
|
Ι |
|
|
|
|
|
|
Ι |
|
|
|
|
& |
|||||
E1 |
|
|
|
Ι5 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
7 |
|
|
|
|
|
8 |
|
|
|
|
|
|
|
J |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0
Рис.1.1
В схеме замещения имеются ветви и узлы, ви общем случае, замкнутые контуры. Ветвью называется любая неразветвленная часть схемы, узлом - пункт соединения нескольких (не менее двух) ветвей. Непрерывная цепочка ветвей, начало которой соединено непосредственно с ее концом, называется замкнутым контуром. Если схема замещения не содержит замкнутых контуров, то она называется разомкнутой.
Каждая ветвь i схемы замещения в общем случае определяется ее полным сопротивлениемZ& ii , действующей в ней э.д..сE& i , проходящим по ней
& |
& |
|
|
|
током Ii и напряжением Ui между ее концами. |
|
|||
В соответствии с законом Ома при указанных на рис.1.2 положитель- |
||||
ных направлениях между этими величинами существует зависимость |
||||
|
& |
& & |
& |
(1.1) |
|
Ui =Zii Ii -Ei . |
|||
Кроме того, между отдельными ветвями i и j схемы замещения могут |
||||
иметь место |
|
& |
обусловленные, |
например, дей- |
взаимные сопротивленияZij , |
||||
ствием взаимной индуктивности. В схеме, обладающей свойством взаимности, взаимные сопротивления не зависят от очередности записи индексов:
Z& ij =Z& ji .
Для ветвей i и j, имеющих взаимные сопротивления, связь между всеми указанными выше величинами определяется при принятых на рис. 1.3 положительных направлениях следующими уравнениями:
& |
& & |
& |
& |
& |
ü |
|
Ui =Zii Ii -Ei + Zij I j ï |
|
|||||
& |
& & |
& |
& |
& |
ý. |
(1.2) |
U j = Zjj I j -E j + Zji Ii ï |
|
|||||
|
|
|
|
|
þ |
|
10

Взаимные сопротивления на схемах замещения не показываются.
|
|
|
|
|
|
|
|
|
|
|
|
Z& |
ii |
|
|
|
& |
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
E i |
|||
& |
|
Ui |
|
|
|
|
|
|
Z |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Z |
|
|
|
|
|
|
& |
& |
|
& |
ij |
& |
|||
|
|
|
|
ii |
|
|
Ei |
|
|
jj |
|
|
|
|
Ej |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Ii |
|
|
|
|
|
|
|
|
|
|
|
||||
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Рис.1.2. |
|
|
|
|
|
Рис.1.3. |
|
|
|||||||
Задающими токами |
& |
(источниками тока) обычно замещается каждая |
||||||||||||||||
J |
||||||||||||||||||
из электрических нагрузок сети. Их |
направление |
|
выбирается противо- |
|||||||||||||||
положным токам нагрузок. |
Источниками |
& |
|
|
|
|
|
|
|
|||||||||
э.д.с. E, как правило, замещаются |
||||||||||||||||||
генераторы электрических станций. При этом один из концов источников тока и э.д.с. соединяются с нейтралью. Величины E& и J& относятся к исходным параметрам режима и являются вынуждающим силами, вызывающими появление токов и напряжений в схеме замещения. Величины Z& ii и Z& ij - парамет-
ры системы. Все они нужны для определения остальных параметров режима: токов в ветвях&Ii , напряжений в узлах U& i и т.д. Если исходные параметры режима и параметры системы остаются независимыми от искомых параметров режима, то схема замещения называется линейной. В случае нелинейных схем замещения применяют приемы их линеаризации.
Установившийся режим электрической цепи синусоидального переменного тока определяется системой линейных алгебраических уравнений. Число уравнений, составляющих систему и подлежащих совместному решению, может достигать десятков и сотен. При этом число ветвейb в схеме всегда
¢ |
|
|
больше, чем число узлов y |
и число независимых контуров k : |
|
|
¢ |
-1. |
|
b = k+ y |
|
Под независимым контуром понимается замкнутый контур схемы, контурное уравнение, для которого не может быть получено в виде линейной комбинации из уравнений для остальных контуров. Как правило, число независимых контуров k меньше числа независимых узлов у , где
y = y¢-1.
Один из узлов схемы является зависимым, т.к. узловое уравнение для него получается путем почленного алгебраического суммирования узловых уравнений для всех остальных узлов схемы. Этот зависимый узел называется
узлом баланса.
Алгебраические уравнения (системы уравнений), определяющие режим схемы замещения, называются в дальнейшем уравнениями состояния. Чаще всего при расчетах рабочих режимов сложных схем в качестве уравнений состояния используются узловые или контурные уравнения, соответствующие первому и второму законам Кирхгофа..
11
Узловое уравнение показывает, что сумма подтекающих к любому узлу токов равна сумме утекающих от него токов:
n |
& |
|
& |
(1.3) |
|
åIi =J. |
||
i=1 |
|
|
Контурное уравнение показывает, что алгебраическая сумма падений |
||
напряжений в любом замкнутом контуре |
равняется |
алгебраической сумме |
э.д.с. вдоль того же контура: |
|
|
n |
|
(1.4) |
åUi =Ek , |
||
& |
& |
|
i=1
где E& k - значение суммарной э.д.с. в контуре, положительное направление которой выбрано совпадающим с направлением соответствующего контурного тока.
Определение установившегося режима электрической сети обычно сводится к решению одной из этих систем уравнений. В общем случае решение может потребовать линейной комбинации из этих уравнений и линейных преобразований полученной системы уравнений. Линейные преобразования системы уравнений проще всего производить, пользуясь специально приспособленным для этого математическим аппаратом - алгеброй матриц.
1.4.Матричная форма записи систем однотипных величин.
При подробной записи системы линейных уравнений(1.3) и (1.4) имеют следующий вид:
& |
& |
& |
& |
& |
& |
& |
ü |
|
a11x1 |
+a12x2 |
+...+a1n xn =b1 |
ï |
|
||||
& |
& |
& |
& |
& |
& |
& |
|
|
|
ý . |
(1.5) |
||||||
a21x1 |
+a22x2 |
+...+a |
2n xn =b2 |
|||||
& |
& |
& |
& |
& |
& |
& |
ï |
|
|
þ |
|
||||||
an1x1 |
+an 2x2 |
+...+ann xn =bn |
|
|||||
Здесь все величины определяются комплексными числами.
В эту систему уравнений входят следующие три группы величин: искомые параметры режимаx&i , свободные члены уравненийbi , определяемые
активными элементами схемыJ& , E& k , и коэффициенты a& ij при неизвестных,
являющиеся параметрами пассивных элементов схемы.
Под пассивными (в отличие от активных) понимаются такие элементы схемы замещения, которые сами не могут вызывать появления в ней токов и напряжений.
Нетрудно заметить, что величины x&i и b&i (параметры режима) имеют по одному индексу, а величины параметров схемы a&ij - по два индекса, из которых первый соответствует номеру строки (т.е. уравнения), а второй - но-
12
меру столбца (т.е. неизвестного). Поэтому число коэффициентов a&ij равно произведению числа неизвестных x&i на число уравнений, т.е. n2 .
Каждую из групп величин x&i и b&i можно записать в виде таблицы, состоящей из одного столбца, т.е. столбцовой матрицы:
|
& |
|
|
& |
|
|
|
|
ù |
éb |
ù |
||
é x |
||||||
ê |
& |
1 |
ú |
ê& |
1 |
ú |
|
|
|
êb2 |
ú |
||
êx2 ú |
||||||
ê . |
ú |
ê |
|
ú |
||
ê |
|
|
ú |
и ê . |
ú . |
|
ê . |
ú |
ê . |
ú |
|||
ê . |
ú |
ê . |
ú |
|||
ê |
|
|
ú |
ê |
|
ú |
êx |
|
ú |
êb |
|
ú |
|
ë |
|
n û |
n |
|||
|
ë |
û |
||||
Такая запись матриц применяется при необходимости выполнения действий с каждым из элементов. Матрицу в целом можно записывать короче,
используя лишь ее общий элемент: |
|
|
|
|
|
|||
& |
n |
и |
é |
& |
ù n |
& |
é& ù |
, |
[xi ]1 |
ëbi û 1 |
или [x] и |
ëbû |
|||||
с указанием пределов изменения индексов i = 1 … n.
Можно применить и условный символ матрицы в виде той же буквы, но другого шрифта.
Несколько иначе записывается таблица коэффициентов a&ij , поскольку
они имеют по два индекса. Пределы изменения этих индексов в рассматриваемом случае одинаковы. Поэтому соответствующая таблица должна иметь столько же строк, сколько она имеет столбцов, т.е. получается квадратной:
éa&11
n êa&21
éëa&ij ùû1 =êê ...
ê
ëa&n1
a12 |
... |
a1n |
ù |
& |
|
& |
ú |
& |
... |
& |
|
a22 |
a2n |
ú . |
|
... |
... ... |
ú |
|
& |
... |
& |
ú |
an2 |
ann |
û |
|
Здесь при записи матрицы с помощью общего элемента пределы изменения индексов указываются у правых черточек. В дальнейшем для сокращения записи они будут опускаться.
Теперь, используя правило умножения матриц, систему уравнений (1.5) можно записать в символическом виде, т.е. с помощью символов матриц:
é& ù |
& |
é& ù |
(1.6) |
ëaij û |
× [xi ] = |
ëbi û . |
Порядок умножения матриц здесь определен заранее, т.к. операцию умножения нужно выполнять строго в той последовательности, в какой она записана.
Записав в указанном виде систему линейных алгебраических уравнений, можно продолжить решение задачи в общем виде. Решение матричного
13
é -1ù
уравнения (1.6) получается просто с помощью обратной матрицы&ij
ëa û.
Умножим уравнение (1.6) слева на éëa&ij-1ùû.
é |
& |
-1 |
ù |
é |
& |
ù |
& |
]= |
é |
& |
-1 |
ù |
é |
& |
ù |
ëaij |
û ëaij û |
[xi |
ëaij û |
ëbi û . |
|||||||||||
Учитывая, что
éëa&ij-1ùû éëa&ij ùû = [1 ],
окончательно получим |
]= |
|
|
-1 |
|
|
|
|
|
|
& |
é |
& |
ù |
é |
& |
ù |
|
(1.7) |
||
|
|
û |
|
|
||||||
[xi |
ëaij |
ëbi û. |
|
|||||||
Такое решение возможно, если |
матрица |
|
é& |
ù |
является неособенной, |
|||||
|
ëaij û |
|||||||||
т.е. ее определитель отличен от нуля.
Следует отметить, что несмотря на кажущуюся простоту решения матричного уравнения объем вычислений остается достаточно большим. Наиболее трудоемкой является операция вычисления обратной матрицы. Однако независимо от сложности технического выполнения этой операции -за пись матричных преобразований с ее использованием значительно упрощает решение многих задач в общем виде.
Таким образом, уравнения состояния схем замещения систем электроснабжения могут быть записаны в виде матричных уравнений, решение которых может быть получено с помощью применения обратных матриц параметров сети. Но для решения конкретных задач матричным методом, в том числе и для записи уравнений состояния в символическом виде, необходимо иметь аналитическое описание схемы соединения ветвей и схемы замещения сети. Это описание может быть получено при использовании некоторых представлений топологической теории графов.
1.5. Топология сети. Элементы теории графов.
Для обобщенного анализа установившихся режимов сложных линейных схем замещения целесообразно использовать топологические методы.
Топология сети - это геометрия сети без рассмотрения ее физического характера (активных сопротивлений, индуктивности и емкостей). Ниже в кратком изложении приводятся необходимые сведения из топологической теории графов.
Граф (система линий) - множество вершин (узлов) и ребер (ветвей). Соединение ребер и вершин между собой образует граф.
Ребро (контур, отрезок линии) является линией, имеющей две конечные точки. Линия может быть направленной, т.е. указывающей из одной точки в другую. Ребро не обязательно должно быть прямой линией, однако оно не пересекает само себя, т.е. не имеет общих точек. В электротехниче-
14
ском смысле ребро может обозначать сопротивление, выпрямителъ и т.д. В общем случае ребру могут приписываться и другие значения, например, ребро может означать процесс между двумя состояниями.
Кратное ребро (параллельный контур) - это совокупность всех ребер, соединявших две одинаковые точки.
Вершина (узел) - конечная точка ребра (ветви) иди одна изолированная точка графа.
Значение вершины и ребра. Вершина может соответствовать узловой точке сети, например, шинам подстанции или сборным шинам электрической станции. Ребра - это соединения вершин, они могут представлять собой действительные связи, например, провода линий.
Соединение (совпадение, инцидентность) возникает, если одна конечная точка ребра совпадает с одной из вершин.
Степень вершины - число ребер, соединенных с этой вершиной. Степень конечной вершины равна единице.
Подграф (частичный граф) - множество ребер графа, выделенных из исходного графа.
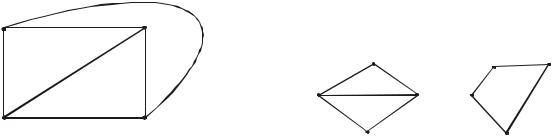
Трасса ребер - это такой ряд ребер, в котором кратность всех ребер равна единице, например, a e c b на рис. 1.4.
Путь - это такая трасса, у которой кратность всех относящихся к ней ребер равна единице, степень промежуточных, вершин - двум, а степень конечных вершин - единице. Так, например, на рис. 1.4 путь составляют ребра a e f. Ребра a e c b не могут составить путь, т.к. степень вершины 1 в данной трассе равна трем.
|
|
в |
d |
3 |
|
1 |
|
f |
с |
|
а |
4 |
е |
|
2 |
|
|
||
|
|
|
|
|
Рис.1.4. |
|
Рис.1.5. |
Длина пути - это число ребер пути. Следовательно, длина одного ребра равна единице.
Связный граф. Граф называется связным, если существует путь между любыми двумя вершинами этого графа. Связный граф представляет собой одно целое. На рис. 1.4 и 1.5 показаны примеры связного и несвязного графов.
15
Контур - однократная последовательность ребер, все вершины которой имеют степень, равную двум. Или другими словами, контур есть замкнутый путь (частичный граф), у которого все относящиеся к нему вершины имеют степень, равную двум. Например, на рис. 1.4 контур может быть образован ребрами a b d.
Дерево - множество ребер, которое не содержит ни одного замкнутого контура, но включает в себя все вершина графа. Иными словами, дерево - это разомкнутая часть замкнутой схемы, которая соединяет все узлы замкнутой схемы. Такая разомкнутая схема получается путем исключения ветвей, входящих в независимые замкнутые контуры схемы. Если поочередно разомкнуть все независимые замкнутые контуры, то одновременно разомкнутся и все прочие контуры и останется разомкнутая часть схемыдерево. Это основная часть схемы, ее "скелет".
Остальные ветви схемы, не вошедшие в дерево схемы, называются хордами, или соединениями графа. Число хорд равно числу независимых контуров схемы.
Ветви дерева - это ветви, которые составляют дерево.
В дереве между двумя узлами существует только один путь. Для электрической сети, имеющей вид дерева, для однозначного определения распределения токов достаточно одних узловых уравнений Кирхгофа. Поэтому в теории цепей понятие "дерево" очень важно.
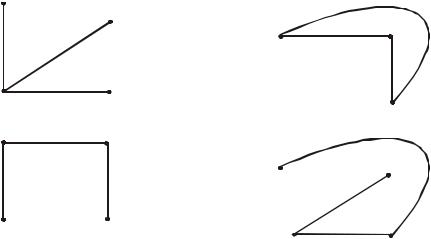
Одна и та же схема может быть разделена на дерево и хордыпо разному. На рис.1.6 показаны две из возможных вариантов разделения графа, представленного на рис.1.4, на дерево и хорды.
3 |
|
1 |
|
|
|
|
|
|
3 |
|
1 |
d |
|
f |
с |
|
в |
|||
|
|
а |
|
|||
4 |
е |
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
|
||
|
в |
|
|
|
|
|
3 |
1 |
|
|
|
|
|
|
|
|
|
d |
||
f |
|
а |
3 |
|
1 |
|
|
|
|
||||
4 |
|
|
|
|
с |
|
|
2 |
4 |
|
е |
|
|
|
|
|
|
2 |
|
Рис.1.6.
Разделение схемы на дерево и хорды позволяет упростить решение ряда задач. Это разделение целесообразно учитывать при нумерации ветвей: вначале нумеруются все ветви, входящие в дерево схемы, а затем - хорды.
16
1.6. Схема замещения электрической сети как связный граф.
Из приведенных кратких сведений теории графов можно сделать -вы вод, что схема замещения электрической сети может рассматриватся как граф. Схема замещения сети обычно является связным графом. Она состоит из ветвей, соединенных в узлы. Эти ветви образуют цепочки(пути графа), которые могут замыкаться и превращаться при этом в замкнутые контуры. Все величины, характеризующие состояние ветвей (токи, э.д.с., напряжения), имеют определенные направления. В связи с этим целесообразно каждой ветви схемы придать любое произвольно выбранное направление. Таким образом, схема замещения сети обычно является связнымнаправленным графом, ребрами которого являются ветви, а вершинами узлы. Так как речь идет о процессах в области электротехники, то в дальнейшем вместо терминов теории графов "вершина" и "ребро" будем применять обычные в электротехнике названия "узел" и "ветвь".
При изображении схем в виде графов нет надобности в специальных обозначениях сопротивлений, э.д.с. и напряжений. Ветви графически изображаются прямой (или кривой) с указанием их направлений. Таким образом, направление ветви от начальной вершины к конечной одновременно является положительным направлением и для всех участвующих величин: э.д.с. E& , тока &I и напряженияU& . В качестве примера не рис.1.7 приведен граф сети, изображенной на рис.1.1. Взаимное сопротивление Z& ij = Z& ji между ветвями i
и j определяет э.д.с., наведенную в ветви j током &Ii , проходящим в ветви I, и наоборот:
E& i =Z& ij ×&I j ,
E& j = Z& ji &Ii .
1 |
2 |
2 |
3 |
|
3 |
|
II |
|
III |
|
4 |
|
|
|
|
||
|
5 |
6 |
7 |
|
4 |
|
I |
|
|
IV |
|
|
|
|
|
|
|
|
1 |
|
|
|
8 |
5
Рис.1.7.
Взаимные сопротивления и проводимости графически не изображаются и не являются ветвями графа. Наличие положительных направлений ветвей освобождает от применения специальных обозначений для определения
17
взаимного расположения ветвей, связанных взаимным сопротивлением. Если
& |
ветви j |
вызывает |
появление положительной э.д.с. |
|
положительный ток I j |
||||
& |
|
& |
между этими ветвями является по- |
|
Ei ветви i , то взаимное сопротивление Zij |
||||
ложительным. Если положительный ток |
& |
ветви j вызывает появление от- |
||
I j |
||||
& |
|
|
|
& |
рицательной э.д.с. Ei в ветвиi , то взаимное сопротивление Zij между этими
ветвями является отрицательным. При этом положительный ток &I j в ветви i
также вызывает появление отрицательной э.д.с. E& j в ветви j.
Для характеристики связей, определяемых графом, пользуются матричными выражениями. В частности, зависимость (1.1), приведенная ранее для отдельной ветви схемы замещения, может быть записана в виде матричного уравнения, справедливого для всей схемы в обобщенном виде:
|
|
|
|
|
|
|
|
|
|
éU ù |
=éZ |
ù éI |
ù-éE ù |
= éU ù |
- éE ù. |
(1.8) |
||||||||
|
|
|
|
|
|
|
|
|
|
ë |
& |
ë |
& |
& |
i û ë |
& |
i û |
ë |
& |
i û |
ë |
& |
i û |
|
|
|
|
|
|
|
|
|
|
|
вi û |
|
вi û ë |
|
|
|
|
||||||||
Здесь |
é |
|
& |
|
|
ù |
- столбцовая матрица напряжений на ветвях схемы; |
|
||||||||||||||||
ëUвi û |
|
|||||||||||||||||||||||
|
|
|
& |
|
|
ù |
- квадратная матрица сопротивлений ветвей; |
|
||||||||||||||||
|
éZ |
|
|
|||||||||||||||||||||
|
ë |
|
|
|
вi û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
é |
& |
|
ù |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ëIi |
û - столбцовая матрица токов ветвей; |
|
|
|
|
|
|
||||||||||||||||
|
|
|
& |
|
|
ù - столбцовая матрица э.д.с. ветвей; |
|
|
|
|
|
|
||||||||||||
|
éE |
|
|
|
|
|
|
|
||||||||||||||||
|
ë |
|
|
i û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
& |
|
ù |
|
& |
& |
ù |
- столбцовая матрица потерь напряжения в ветвях. |
||||||||||||||
|
éU |
= éZ |
ù éI |
|||||||||||||||||||||
|
ë |
|
|
|
i û |
ë |
|
вi û ë |
вi û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение (1.8) остается справедливым для любого направленного графа, которым представляется схема замещения электрической сети.
Таким образом, выбор направления для всех ветвей схемы определяет знаки для всех параметров схемы и параметров ее режима. Применение элементов теорий графов позволяет еще более рационализировать обобщенные записи математических соотношений и аналитическое решение задач.
1.7. Матрица соединений.
Матрица соединений, или, как ее иначе называют, первая матрица инциденций была впервые введена Пуанкаре. Она служит для обобщенного аналитического представления схемы соединений узлов и ветвей в направленном графе. При этом используются коэффициенты соединений(инцидентности).
Вматрице соединений строки соответствуют номерам узлов, а столбцы
-номерам ветвей. На пересечении строки i и столбца j располагаются коэффициенты соединений. Коэффициент соединений равен положительной единице, если ветвь j соединена с узлом i своей начальной вершиной, т.е. имеет направление от данного узла i . На пересечении строки i и столбца j помеща-
18

ется отрицательная единица, если ветвь j направлена к узлу i . Наконец, коэффициент соединений равен нулю, если ветвь j не соединена с узлом i непосредственно.
Каждая строка матрицы соединений для всей схемы[MS ] показывает,
какими вершинами присоединяются соответствующие ветви к данному узлу схемы. Каждый столбец показывает, какие узлы являются начальной и конечной вершинами данной ветви. В каждом столбце матрицы[MS ] может
быть только одна положительная и одна отрицательная единицы. Остальные элементы столбца равны нулю. Поэтому, если сложить все строки по столбцам, получится нулевая строка:
[nt ][MS ]=[0]. |
(1.9) |
Здесь операция сложения элементов матрицы[MS ] по столбцам вы-
полнена путем умножения ее слева на единичную матрицустроку[nt ] . Из
(1.9) следует, что определитель матрицы [MS ] равен нулю.
В качестве примера ниже приведена матрица соединений графа, показанного на рис. 1.7 и имеющего 5 узлов и 8 ветвей:
|
|
|
é-1 1 |
0 |
0 |
1 |
0 |
0 |
0 ù |
ü |
|||
|
|
|
ê |
0 |
-1 1 |
0 |
0 |
1 |
0 |
0 |
ú |
ï |
|
[ |
|
S |
ê |
ú |
ï |
||||||||
M |
] |
|
0 |
-1 1 |
0 |
0 |
1 |
1 |
ú |
ý |
|||
|
|
= ê 0 |
ïузлы |
||||||||||
|
|
|
ê |
0 |
0 |
0 |
-1 0 |
0 |
0 |
0 |
ú |
ï |
|
|
|
|
ê |
ú |
ï |
||||||||
|
|
|
ê |
1 |
0 |
0 |
0 |
-1 -1 -1 -1ú |
ï |
||||
|
|
|
ë |
|
|
|
|
|
|
|
|
û |
þ |
ветви
По матрице [MS ] можно восстановить схему соединений. Матрица
[MS ] полностью замещает схему и дает возможность выполнить анали-
тическое решение задачи в общем виде. Полученное решение оказывается справедливым для любой схемы. В развернутом виде эта матрица нужна только для выполнения численного расчета для конкретной схемы.
Выделим в матрице [MS ] строку, соответствующую опорной вершине
(базисному узлу), которая совпадает, как правило, с узлом баланса. Если принять номер выделенной строки последним, то, разделив матрицы на бло-
ки, условие (1.9) можно записать в следующем виде: |
|
[nt 1 êé] M úù =[0 ]. |
(1.10) |
ëMб û |
|
19
Здесь [M] - матрица соединений для схемы за исключением базисного узла;
[Mб ] - матрица соединений для базисного узла.
Полученный результат означает, что одну из строк матрицы можно получить путем суммирования всех остальных строк и изменения знаков всех элементов суммарной матрицы на обратные:
[Mб ]=-[nt ][M]. |
(1.11) |
Поэтому для практических расчетов достаточно пользоваться матрицей [M]для всей схемы, за исключением базисного узла. По этой матрице вся схема также может быть восстановлена.
Для замкнутой схемы матрица[M] получается прямоугольной. Для разомкнутой схемы, в том числе и для дерева графа, [M]получается квадрат-
ной и обозначаетсяéëMp ùû . Ее определитель равен +1 или -1, и она имеет об-
ратную матрицу, элементами которой тякже являются +1, -1 и 0.
1.8. Матрица контуров.
Матрица контуров [N] (вторая матрица инциденций) служит для обобщенного аналитического описания соединений ветвей схемы в -неза висимые замкнутые контуры. Наряду с матрицей [M], она дает допол-
нительную характеристику схемы. Строки матрицы [N] соответствуют неза-
висимым контурам схемы, а столбцы - ветвям. Наличие соединений здесь также определяется коэффициентами инцидентности. На пересечении строки i и столбца j матрицы помещают положительную единицу, если ветвь j входит в контур i и имеет направление, совпадающее с направлением контура. Отрицательная единица показывает, что ветвь j входит в состав контура i , но имеет направление, противоположное направлению обхода контура. Нуль ставится, если ветвь j не входит в контур i .
Матрица [N] получается прямоугольной. Число строк ее равно числу
независимых контуров, а число столбцов - числу ветвей. В каждом ее столбце должна быть по меньшей мере одна положительная или отрицательная единица. В каждой строке матрицы должно быть как минимум три положительных или отрицательных единицы, т.к. замкнутый контур не может состоять из меньшего количества ветвей(если схема не содержит параллельных ветвей).
В качестве примера ниже приведена матрица[N] для графа, пока-
занного на рис. 1.7 и имеющего восемь ветвей и четыре независимых контура.
20

Вид матрицы [N] зависит от выбора независимых контуров и принятых направлений его обхода. Одному и тому же графу сети в зависимости от выбора независимых контуров может соответствовать несколько матриц[N].
ветви
|
|
é 1 |
0 |
0 |
0 |
1 |
0 |
0 |
0ù ü |
|
|||
|
|
ê |
0 |
1 |
0 |
0 |
-1 1 |
0 |
0 |
ú |
ï |
|
|
[ |
] |
ê |
ú |
ï |
контуры |
||||||||
|
|
|
|
|
|
|
|
|
|
ý |
|||
|
N = |
ê |
0 |
0 |
1 |
0 |
0 |
-1 1 |
0ú |
ï |
|||
|
|
|
|||||||||||
|
|
ê |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
1 |
ú |
ï |
|
|
|
ë |
û |
þ |
|
||||||||
В отличие от матрицы[M] матрица [N] не дает возможности восстановить схему, т.к. соединение ветвей в узлах схемы по матрице контуров остается неизвестным. Одной и той же матрице[N] могут соответствовать разные схемы соединения ветвей в узлах. Это значит, что матрица [N] не дает полной информации о схеме соединений.
Как уже указывалось, матрица [N] прямоугольная. Поскольку прямо-
угольная матрица обратной не имеет, то ее целесообразно разделить на блоки так, чтобы одна из подматриц получилась квадратной. Такое разделение на блоки удобно производить в соответствии с делением схемы на дерево и хорды. При этом рекомендуется следующий порядок нумерации ветвей схемы. Вначале нумеруются ветви дерева, а затем хорды. Каждой ветви дерева дается номер ее конечного узла, а хорды нумеруются в той же последовательности, в которой пронумерованы соответствующие независимые контуры.
Кроме того, направления обхода указанных независимых контуров должны совпадать с направлением соответствующих хорд. При этом целесообразно так выбирать независимые контуры, чтобы каждая из хорд входила только в какой-либо один независимый контур схемы.
Матрицу [N] можно представить состоящей из двух матриц: [Na ]- со-
|
é ù |
|
|
1 |
|
ответствующей ветвям дерева графа, и |
- соответствующей хордам . |
||||
ëNb û |
|||||
[N]= |
é |
ù |
|
|
|
ëNa Nb û. |
|
|
|||
При указанном порядке нумерации ветвей матрица |
é ù |
квадратной и еди- |
|||
ëNb û |
|||||
ничной.
В дальнейшем при разделения матриц на блоки подматрицы с индексом α будут также соответствовать дереву схемы, а с индексом β- хордам.
21

1.9. Зависимости между токами и напряжениями электрической цепи.
Рассмотрим на примере, каким образом может быть получена матричная форма записи уравнений состояния.
На рис.1.8 приведен граф схемы замещения электрической сети, имеющий три независимых узла и два независимых контура. Активными элементами в схеме являются задающий ток J&2 в узле 2 и источник э.д.с. E& 4 в ветви 4. Для этой схемы в соответствии с законами Кирхгофа можно записать для независимых узлов схемы узловые, а для независимых контуров контурные уравнения в следующем виде.
|
|
|
|
|
& |
|
|
|
|
||
1 |
2 |
|
J 2 |
3 |
|||||||
|
3 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
II |
|
|
|||
|
|
|
|
I |
|
|
|
|
|||
|
|
1 |
|
4 |
|
|
5 |
|
|||
|
|
|
|
|
|
|
|
|
|
||
4
Рис.1.8
Узловые уравнения:
узел 1: -&I1 +I&2 +0 +0 +0 =0;
узел 2: 0-I&2 +I&3 +I&4 +0 =J&2 ; узел 3: 0+0 -&I3 +0 +&I5 =0.
В качестве узла баланса (базисного узла) принят узел 4. Контурные уравнения:
контур 1: |
& |
|
& |
+0 |
& |
|
|
|
|
|
|
|
|
|
& |
|
|
|
UВ1 |
+ UВ2 |
+UВ4 +0 |
= 0 +0 + 0 +E4 +0; |
|
||||||||||||||
контур 2: |
& |
|
& |
& |
& |
|
|
= 0 |
+0 + 0 +0 +0. |
|
||||||||
UВ1 |
+ UВ2 |
+UВ3 +0 +UВ5 |
|
|||||||||||||||
Эти две системы уравнений, записанные в матричной форме, будут |
||||||||||||||||||
иметь вид: |
|
|
|
|
|
|
|
éI |
ù |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
é-1 1 0 0 0ù |
ê |
&1 |
ú |
|
é |
0 ù |
|
|
||||||||
|
|
êI2 ú |
|
|
|
|||||||||||||
|
|
ê |
0 -1 |
1 1 |
0 |
ú |
|
& |
|
ú |
= |
ê |
& |
|
ú |
, |
(1.12) |
|
|
|
ê |
ú |
×êI |
3 |
ê |
J |
2 |
ú |
|||||||||
|
|
|
|
|
|
ê |
|
ú |
|
|
|
|
||||||
|
|
ê |
0 0 |
|
|
ú |
& |
|
|
ê |
0 |
ú |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
ë |
-1 0 1û |
êI4 |
ú ë |
û |
|
|
||||||||||
|
|
|
|
|
|
|
|
ê |
& |
|
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ëI5 |
û |
|
|
|
|
|
|
|
||
22
|
|
éUВ1 |
ù |
|
é |
0 ù |
|
|
|
|
& |
|
|
|
|
|
|
é1 1 0 1 0ù |
ê & |
ú |
|
ê |
0 |
ú |
|
|
êUВ2 |
ú |
é1 1 0 1 0ù ê |
ú |
(1.13) |
||||
ê |
ú |
êUВ3 |
ú |
= ê |
ú ê |
0 ú |
||
|
|
& |
|
|
|
|
|
|
ë1 1 1 0 1û ê & |
ú ë1 1 1 0 1û ê |
& |
ú |
|
||||
|
|
êUВ4 |
ú |
|
êE4 |
ú |
|
|
|
|
ê & |
ú |
|
ê |
0 |
ú |
|
|
|
ëUВ5 |
û |
|
ë |
û |
|
|
Нетрудно видеть, что матрица - множимое в уравнении (1.12), состоящая из 1, -1 и 0, представляет собой матрицу соединения[M]. Матрицы -
множимое в уравнении (1.13), являются матрицами контуров[N]. Следова-
тельно, уравнения состояния можно записать в матричной форме, используя матрицы инциденций.
é&ù |
= |
é&ù |
; |
|
(1.14) |
Узловое уравнение [M]ëIû |
ëJû |
|
|||
|
& |
|
|
& |
(1.15) |
Контурное уравнение [Ν]ëéUВ ûù = [Ν]ëé |
Εûù. |
||||
Учитывая, что падение напряжения на ветви равно произведению -со противления ветви Z& bi на ее ток &Ii , контурное уравнение можно переписать в следующем виде:
|
|
|
|
[N]éZ |
ù éIù |
= [N] éEù |
= éE |
ù . |
(1.16) |
||||||
|
|
|
|
ë |
& |
|
& |
û |
ë |
& |
û |
ë |
& |
k û |
|
|
|
|
|
В û ë |
|
|
|
|
|||||||
Здесь через |
|
& |
ù |
обозначена столбцовая матрица контурных э.д.с. |
|||||||||||
éE |
|||||||||||||||
|
ë |
|
k û |
|
|
|
|
|
|
|
|
|
|
|
|
Уравнения |
(1.14) |
и (1.15) |
представляют |
собой всю |
систему алгеб- |
||||||||||
раических уравнений состояния схем замещения электрических цепей. В таком виде они справедливы для любых схем, в том числе и для нелинейных цепей.
Полученные в матричной форме узловое и контурное уравнения сос-
|
|
|
|
|
|
|
|
|
|
|
[ |
] |
[ |
]ë |
& |
В û |
тояния можно |
|
объединить в одно, если |
|
матрицы |
|
M |
и |
N éZ |
ù рас- |
|||||||
сматривать как блоки одной объединенной матрицы параметров системы |
||||||||||||||||
|
|
|
|
|
|
[ |
A = |
é M |
ù , |
|
|
|
|
|
|
|
|
|
|
|
|
|
] |
ê |
|
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ëN ZВ û |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
& |
и |
& |
|
& |
ù |
рассматривать как блоки одной объединенной |
||||||||||
а матрицы éJù |
éNEù |
= éE |
||||||||||||||
ë û |
|
ë û |
ë |
|
k û |
|
|
|
|
|
|
|
|
|
|
|
матрицы исходных параметров режима
é J& ù é J& ù éF& ù =ê ú =ê ú. ë û ëNE& û ëE& k û
При этом обобщенное уравнение состояния принимает следующий вид:
éA& ù é&Iù= éF& ù. (1.17) ë û ë û ë û
23
|
é & ù |
|
|
|
|
Здесь матрица ëAû является квадратной и в обычных условиях неособенной. |
|
||||
Поэтому полученное уравнение состояния можно решить относительно мат- |
|
||||
рицы токов ветвей: |
é & -1 |
|
|
|
|
|
é&ù |
ù é & ù |
(1.18) |
|
|
|
ëIû |
=ëA |
û ëFû. |
|
|
Зная токи, можно определить все остальные параметры режима непосред- |
|
||||
ственно без решения какой-либо системы уравнений. |
|
|
|||
|
Преимуществом такого общего решения является, в частности, то, что |
|
|||
простая запись его может быть |
использована для |
дальнейших- |
пр |
||
образований и получения соотношений между матрицами отдельных вели- |
|
||||
чин в других более целесообразнах формах. С точки же зрения решения кон- |
|
||||
кретных задач такое объединение уравнений состояния не является наиболее |
|
||||
|
é & ù |
достаточно высок и получение матрицы |
|
||
удачным, т.к. порядок матрицы ëAû |
|
||||
é & -1 |
ù |
|
|
|
|
ëA |
û вызывает затруднения. |
|
|
|
|
2. Методы расчета установившихся режимов электрических сетей.
2.1. Классификация методов расчета.
Как известно, все формы уравнений, описывающих режим электрической сети, являются следствием двух матричных уравнений состояния цепи, отвечающих двум законам Кирхгофа.
Непосредственное применение уравнений Кирхгофа приводит к“прямому” методу расчета, основанному на решении матричного уравнения (1.17)
“Прямой” метод расчета связан с необходимостью решения тем или иным методом систем уравнений, число которых равно числу ветвей в направленном графе схемы. Стремление уменьшить число узловых уравнений привело к появлению метода контурных токов. Первый из них сводит задачу к определению узловых напряжений, число которых равно числу узлов схемы (без базисного узла). Второй метод приводит к решению уравнений, определяющих контурные токи. В обоих случаях число неизвестных и соответственно число уравнений в системе, определяющей параметры режима, оказывается меньше числа ветвей в схеме. Кроме того, можно выделить третье направление, определяющее параметры режима сети на основе метода наложения через обобщенные параметры схемы. Практически уравнения этого метода могут быть получены с помощью двух первых методов.
Каждая из выделенных групп уравнений может непосредственно -ис пользоваться для определения параметров режима электрических сетей. Вместе с тем эти уравнения служат основой для ряда методов расчета, преду-
24
