
- •Шайкин а.Н.
- •Операции над строками матрицы
- •Ступенчатые матрицы
- •Отбросим первую строку. Оставшаяся матрица имеет строку. По индуктивному предположению ее можно привести к ступенчатому виду:
- •Линейная зависимость строк матрицы
- •Ранг матрицы. Базисные строки
- •Определители
- •Операции над матрицами
- •Обратная матрица
- •Системы линейных уравнений
- •Тогда в матричной записисистема линейных уравнений может быть записана в виде.
- •Специальный случай.
- •Раскладывая определитель по первой строке, имеем
- •Критерий совместности Вернемся к произвольной системе mуравнений сnнеизвестными.
- •Однородные системы
- •С использованием этой фундаментальной системы решений общее решение однородной системы записывается в виде , где– произвольные константы.
Раскладывая определитель по первой строке, имеем
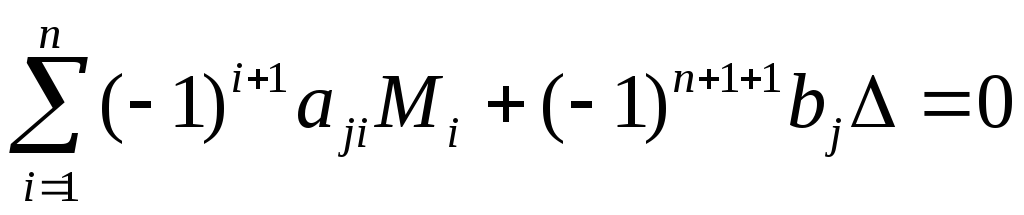 ,
,
где
![]() – определитель матрицы, полученной из
расширенной матрицы системы вычеркиваниемi-го
столбца. Тогда
– определитель матрицы, полученной из
расширенной матрицы системы вычеркиваниемi-го
столбца. Тогда
 .
.
Поскольку
![]() ,
можно написать
,
можно написать
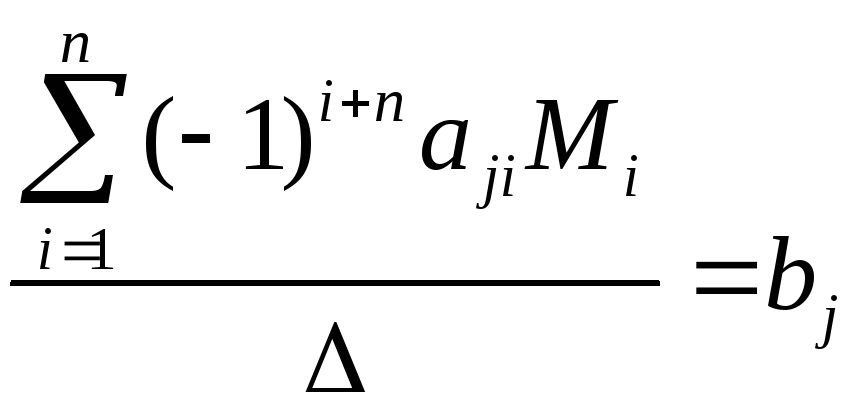
![]()
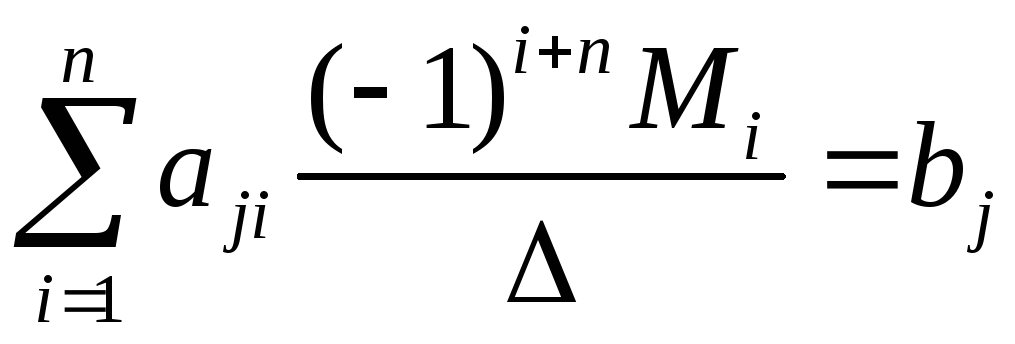 ,
,
откуда,
сравнивая с
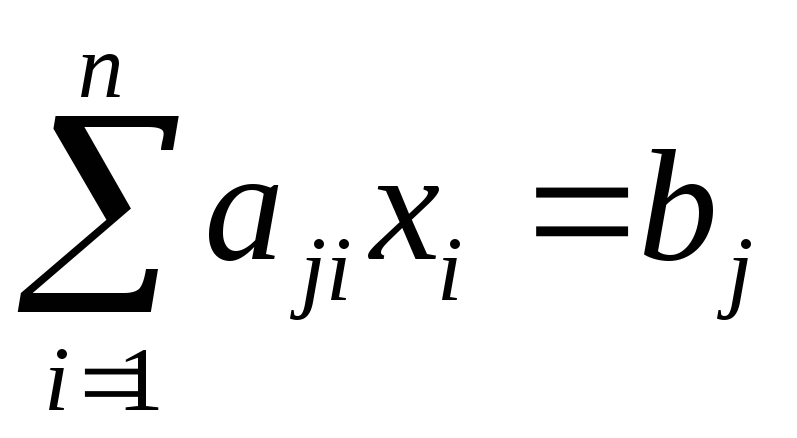 ,
делаем вывод, что
,
делаем вывод, что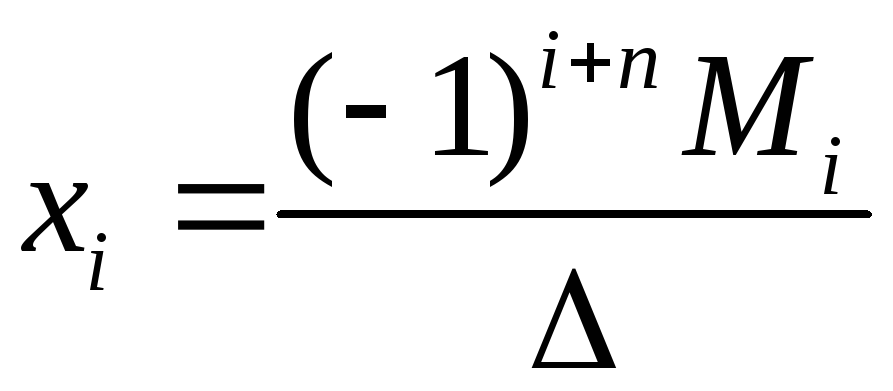 (
(![]() )
удовлетворяютj-му
уравнению системы. Поскольку выражения
для
)
удовлетворяютj-му
уравнению системы. Поскольку выражения
для
![]() не зависят отj,
то они удовлетворяют всем уравнениям
системы. Тем самым существование решения
доказано. Учитывая, что
не зависят отj,
то они удовлетворяют всем уравнениям
системы. Тем самым существование решения
доказано. Учитывая, что
![]() ,
получаем нужный вид для формул Крамера:
,
получаем нужный вид для формул Крамера:
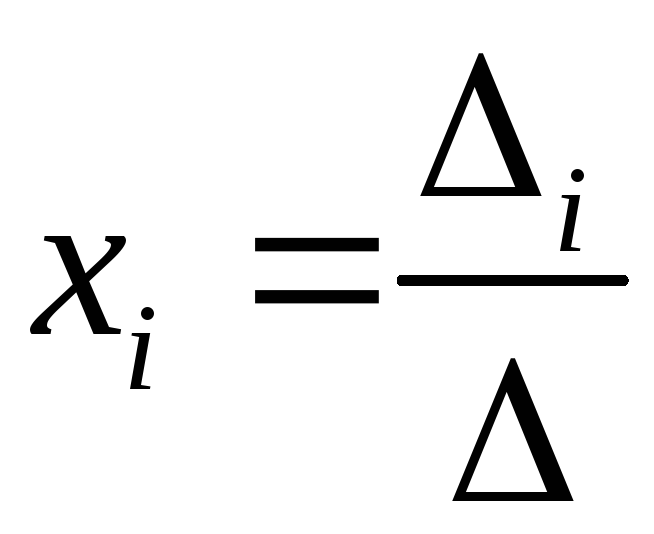 .
.
Осталось
доказать единственность полученного
решения. Предположим, есть два решения
![]() и
и![]() .
Подставим эти решения в систему:
.
Подставим эти решения в систему:![]() и
и![]() .
Тогда
.
Тогда
![]() ,
,
поскольку существование обратной матрицы гарантируется ненулевым определителем матрицы А.■
Также
системы линейных уравнений
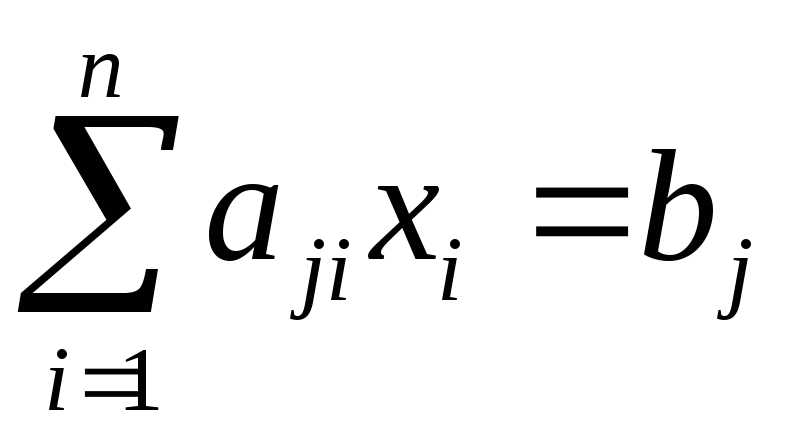 (j=1,2,…,m)
с квадратной матрицей, определитель
которой неравен нулю, можно решать с
помощью нахождения обратной матрицы,
или другими словами, решая матричное
уравнение
(j=1,2,…,m)
с квадратной матрицей, определитель
которой неравен нулю, можно решать с
помощью нахождения обратной матрицы,
или другими словами, решая матричное
уравнение ![]() .
Поскольку
.
Поскольку
![]() ,
обратная матрица
,
обратная матрица![]() существует. Поэтому
существует. Поэтому![]() – решение системы.
– решение системы.
Критерий совместности Вернемся к произвольной системе mуравнений сnнеизвестными.
Теорема (Кронекер – Капелли). Система линейных уравнений совместна тогда и только тогда, когда ранг ее матрицы равен рангу расширенной матрицы.
Доказательство. Покажем, что если к матрице системы применить элементарное преобразование строк, то система, соответствующая полученной матрице, будет равносильна изначальной системе.
Элементарному преобразованию первого типа соответствует перемена местами двух строк системы. Очевидно, новая система будет равносильна старой.
Элементарному
преобразованию второго типа соответствует
замена одной из строк (например i-й)
системы на сумму этой строки и другой
строки (например j-й)
системы, умноженной на какое-либо число
(например
![]() ).
Поскольку от новой системы к старой
также можно перейти с помощью одного
преобразования строк второго типа, то
достаточно показать, что всякое решение
старой системы будет решением новой.
Пусть
).
Поскольку от новой системы к старой
также можно перейти с помощью одного
преобразования строк второго типа, то
достаточно показать, что всякое решение
старой системы будет решением новой.
Пусть
![]() –
решение старой системы. Сомнение может
вызвать толькоi-е
уравнение новой системы. Однако выкладки
–
решение старой системы. Сомнение может
вызвать толькоi-е
уравнение новой системы. Однако выкладки
![]()
![]()
![]()
рассеивают это сомнение.
Элементарному преобразованию третьего типа соответствует умножение какой-нибудь строки системы на ненулевое число. Очевидно, новая система будет равносильна старой.
Теперь приведем расширенную матрицу систему к ступенчатому виду Гаусса. Поскольку при этом столбцы не менялись местами, то тем самым оказалась приведенной к ступенчатому виду и матрица (нерасширенная) системы. Система, соответствующая ступенчатому виду расширенной матрицы, равносильна изначальной системе.
Возможны два случая.
Существует строка в ступенчатом виде расширенной матрицы, в которой опорный элемент находится в столбце свободных членов. Очевидно, что расширенная матрица имеет ранг, на единицу больший, чем ранг матрицы системы. С другой стороны, соответствующее такой строке уравнение системы решений не имеет.
Если указанной строки нет, то ранг расширенной матрицы равен рангу матрицы системы. Покажем, что в этом случае система совместна. Пусть ранг равен r, а опорные элементы располагаются в столбцах с номерами
 ,
причем
,
причем .
Тогда неизвестные
.
Тогда неизвестные можно
объявить
главными
(базисными),
а остальные можно
объявить свободными.
Кроме того, отбросим уравнения полученной
системы, соответствующие нулевым
строкам в ступенчатом виде Гаусса
расширенной матрицы, что дает системе,
равносильную исходной. Перенеся
свободные неизвестные в правую часть,
придем к системе
можно
объявить
главными
(базисными),
а остальные можно
объявить свободными.
Кроме того, отбросим уравнения полученной
системы, соответствующие нулевым
строкам в ступенчатом виде Гаусса
расширенной матрицы, что дает системе,
равносильную исходной. Перенеся
свободные неизвестные в правую часть,
придем к системе

где
через
![]() обозначена сумма свободных неизвестных,
умноженных на стоящие перед ними
коэффициентыi-го
уравнения. Поскольку коэффициенты
обозначена сумма свободных неизвестных,
умноженных на стоящие перед ними
коэффициентыi-го
уравнения. Поскольку коэффициенты
![]() отличны от нуля, то при отсутствии
свободных переменных имеем единственное
решение, а при наличии свободных
переменных, придавая им различные
значения, однозначно определяем главные
неизвестные и, тем самым, имеем бесконечно
много решений. Придавая свободным
переменным всевозможные значения,
получим общее решение системы.■
отличны от нуля, то при отсутствии
свободных переменных имеем единственное
решение, а при наличии свободных
переменных, придавая им различные
значения, однозначно определяем главные
неизвестные и, тем самым, имеем бесконечно
много решений. Придавая свободным
переменным всевозможные значения,
получим общее решение системы.■
Таким образом, система имеет единственное решение, когда ранг ее матрицы равен рангу ее расширенной матрицы и числу неизвестных и меньше или равен числу уравнений, т. е. отсутствуют свободные неизвестные.
При доказательстве теоремы Кронекера – Капелли общее решение совместной системы было получено методом, который называется метод Гаусса.
1.
Составить расширенную матрицу (А|![]() )
и привести ее к ступенчатому виду с
помощью элементарных преобразований
строк.
)
и привести ее к ступенчатому виду с
помощью элементарных преобразований
строк.
а. Если существует строка в ступенчатом виде расширенной матрицы, в которой опорный элемент находится в столбце свободных членов, то система несовместна и решение окончено.
б. Если такой строки нет, то система совместна, главными переменными объявляем те, которые соответствуют базисным столбцам, а остальные переменные объявляем свободными.
2. Привести ступенчатую матрицу к ступенчатому виду Гаусса.
Написать систему линейных уравнений, соответствующую матрице, построенной на шаге 2, обозначив свободные неизвестные числами
 .
.Выразить из полученной системы главные неизвестные через свободные.
Записать общее решение в виде
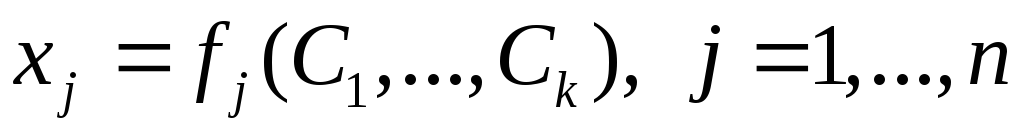 .
.
