Однородные системы

Линейная однородная система алгебраических уравнений всегда совместна, т. к. всегда имеет нулевое решение , называемое тривиальным. Поэтому интересно выяснить, когда имеются нетривиальные решения.

Теорема. Линейная однородная система алгебраических уравнений имеет нетривиальные решения тогда и только тогда, когда ее ранг меньше числа неизвестных.

Доказательство. Приведем данную однородную систему к ступенчатому виду. Очевидно, она при этом останется однородной. Также ясно, что число главных неизвестных равно рангу системы. Следовательно, существуют свободные неизвестные, что в соответствии с методом Гаусса обеспечивает существование ненулевых решений.■

Теорема. Линейная однородная система алгебраических уравнений, у которой число уравнений равно числу неизвестных имеет нетривиальные решения тогда и только тогда, когда определитель ее матрицы равен нулю.

Доказательство. Линейная однородная система алгебраических уравнений имеет нетривиальные решения тогда и только тогда, когда ее ранг меньше числа неизвестных, а значит меньше числа строк. Таким образом, линейно независимых строк меньше общего числа строк, т. е. все строки матрицы будут линейно зависимы. Тогда определитель матрицы равен нулю.■

Теорема. Множество решений линейной однородной системы алгебраических уравнений является линейным векторным пространством.

Доказательство. Поскольку решения можно рассматривать как вектора и нулевой вектор всегда принадлежит множеству решений, достаточно проверить линейность. Пусть и– два решения однородной системы. Покажем, чтои– тоже решения этой системы. Для этого подставим их вi-е уравнение системы:

0,

.■

Теорема. Пространство решений линейной однородной системы алгебраических уравнений с n неизвестными и матрицей ранга r имеет размерность k=n–r.

Доказательство. В соответствии с методом Гаусса, в общем решении свободные переменные могут принимать произвольные значения, их количество равно k=n–r, а главные переменные определяются через свободные однозначно.■

Тогда любой упорядоченный набор из k=n–r линейно независимых решений однородной системы образует базис в пространстве решений.

Определение. Фундаментальной системой решений линейной однородной системы алгебраических уравнений называется базис в пространстве решений этой системы.

Особо выделяют фундаментальную систему решений, состоящую из вектор-столбцов , получаемых из общего решения однородной системы подстановкой вместо вектора свободных неизвестныхпоочередно следующих векторов

.

С использованием этой фундаментальной системы решений общее решение однородной системы записывается в виде , где– произвольные константы.

Теорема. Общее решение совместной неоднородной системы равно сумме ее частного решения и общего решения соответствующей однородной системы.

Доказательство. Покажем, что сумма любого решения неоднородной системы и любого решения соответствующей однородной системы есть решение неоднородной системы. Пусть и– решения однородной и неоднородной систем, соответственно. Подставляя в любое (например, вi-е) уравнение неоднородной системы на место неизвестных сумму этих решений, получаем .

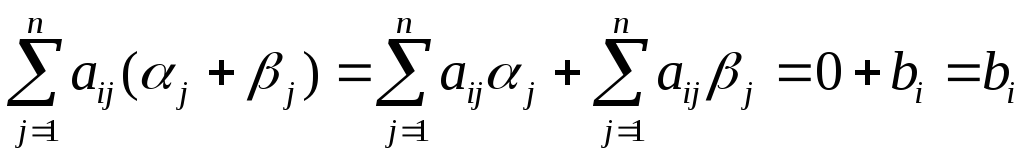Теперь покажем, что разность двух произвольных решений неоднородной системы является решением соответствующей однородной системы. Пусть и– два решения неоднородной системы. Подставляя в любое (например, вi-е) уравнение однородной системы на место неизвестных разность этих решений, получаем .

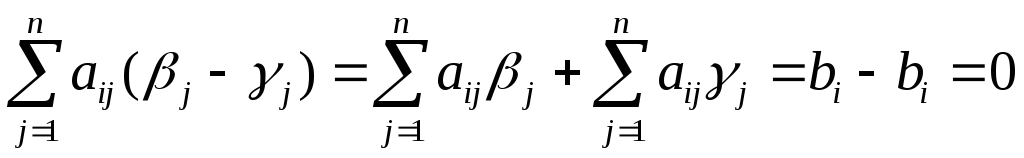Из доказанного вытекает, что, найдя одно решение неоднородной системы и складывая его с каждым решением соответствующей однородной системы, мы получим все решения неоднородной системы.■