Глава одиннадцатая. Цепи несинусоидального тока

11.1. Общие и методические замечания

В настоящей главе рассматриваются цепи с периодическими токами и напряжениями, форма которых отличается от гармонической. Изучавшиеся до сих пор гармонические токи и напряжения являются лишь частным случаем более общих-несинусоидальных процессов в цепях.

Практически все генераторы переменного тока генери­руют не чисто гармонические колебания, а периодические несинусоидальные. Источниками несинусоидальности могут быть неоднородности магнитного поля в зазоре генератора электроэнергии, переключения b преобразователях перемен­ного тока, нелинейности в электронных генераторах.

Следует указать еще на один существенный источник ис­кажений формы кривой напряжения и тока - мощныенели­нейные и нестационарные нагрузки. В энергетике это, на­пример, дуговые сталеплавильные печи или мощные выпря­мительные установки.

В тех случаях, когда требуется мощный источник пере­менного тока для энергетических целей - форма кривой его напряжения или тока должна быть близка к синусои­дальной (требования к синусоидальности жестко регламентируются. Несинусондальность источника энергии играет отрицательную роль главным образом при питании электрических машин, поскольку приводит к снижению вращаю­щего момента, повышенному нагреву двигателей, генерато­ров и трансформаторов и вытекающему отсюда ускорению старения изоляции. Некоторые формы кривых периодическо­го несинусоидального напряжения показаны на рис. 11.1а, б.

Во многих случаях несинусоидальность токов или напря­жений является полезным эффектом,

например, в схемах выпрямления кривая напряжения несинусоидальна (рис. l1.l в, г). В цепях

передачи и переработки информации напряжения и токи существенно несинусоидальны. Это

могут быть импульсные сигналы различной формы, например прямоугольные (рис. 11.1д, е) или

импульсы линейно изменяющегося напряжения (рис. 11.1 ж), применяемые, в частно­сти, в цепях

развертки телевизора.

Рис.11.1.(а)

Рис.11.1.(б)

Рис.11.1.(в)

Рис.11.1.(г)

Рис.11.1.(д)

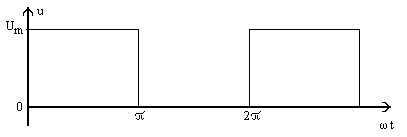Рис.11.1.(е)

Рис.11.1.(ж)

Рис. 11.1а, б, в, г, д , е, ж

Цель настоящей главы —рассмотрение методов расчета и анализа линейных цепей, питаемых

источниками периоди­ческих несинусоидальных ЭДС и токов. Основной метод анализа -

- разложение несинусоидальных кривых ЭДС и тока в тригонометрический ряд Фурье и расчет цепи по принципу наложения, под действием источников каждой частоты в от­дельности.

При изучении материала этой главы следует вспомнить— в чем заключается принцип и метод наложения. Расчет ли­нейных цепей несинусоидального тока тесно связан с комп­лексным методом, поэтому нужно знать его основные поло­жения. Так как один из этапов расчета цепей несинусоидального тока связан с разложением периодической несину­соидальной функции в дискретный ряд Фурье, следует ос­вежить знания по теории рядов.

11.2. Разложение периодических несинусоидальных кривых напряжения и тока в тригонометрический ряд

Рассматривается несинусоидальная перидическая функция с периодом, например, напряжениеили токТребуется разложить эту функцию в тригонометрический ряд

(ряд Фурье).

Ряд Фурье имеет вид

(11.1)

где Uo—постоянная составляющая напряжения;иамшлитуды косинусной и синусной составляющихR-й гармо­ники напряжения соответственно.

Эти величины вычисляются по известным формулам раз­ложения Фурье:

(11.2)

Каждую гармоническую составляющую можно представить в полярной системе координат

(11.3)

где

или

Тогда ряд Фурье будет записываться следующим образом

(11.4)

Совокупность гармонических составляющих функцииназывается спектром. Спектр

представляет собой дис­кретный ряд гармоник с частотами , где= 0, 1, 2, ...с амплитудами

и фазами(постоянная составляющаяUoздесь представляет собой амплитуду

напряжения нуле­вой гармоники при ). Такой спектр называется дискрет­ным, или

линейчатым, и изображается графически в виде диаграмм, где по оси абсцисс откладываются

частоты гар­моник, а по оси ординат соответствующие амплитуды (амп­литудный спектр) или

фазы (фазовый спектр).

В случаях симметрии формы несинусоидальнои кривой (напряжения или тока) вид, разложения в ряд Фурье упро­щается, а именно:

1. Если функция нечетна, т. е. симметрична относительно начала координат (например, рис. 11.1а,д ), то

и в разложении Фурье содержатся только синусные составляющие

(11.5)

2. Если функция четная, т. е. симметрична относительно оси ординат

(например, рис. 11.1в), то

и в разложении Фурье содержатся только постоянная и косинусные составляющие

(11.6 )

3.Если функциясимметрична относительно оси абсцисс (например, рис. 11.1б), то

и в разложении Фурье содержатся только нечетные гармо­ники.

В ряде случаев необходимо разложить в ряд Фурье функ­цию, смещенную на некоторый угол а

относительно функ­ции, разложение которой известно. Пусть дано разложение Фурье

тогда разложение смещенной функции имеет вид

(11.7)

где значения определяются по формулам (11.2);

— угол смещения начала координат по оси.

Пример 11.1.Определить постоянную составляющую, первую и вторую гармоники

разложения и ряд Фурье кривой двухполупериодного выпрямленного напряжения ( рис.11.1в)

при .

Решение

Кривая имеет вид

Для разложения в ряд Фурье используем формулы (11,2). При определении коэффициентов

Фурье учтем симметрию кривой относительно оси ординат. В разложении содержат­ся

постоянная и косинусные составляющие.

Постоянная составляющая напряжения

Здесь при интегрировании учтено, что кривая напряжения состоит из повторяющихся дважды за

период полусинусоид, поэтому интегрирование проводится в пределах полусинусои­ды.

После подстановки , получаем.

Коэффициент при первой гармонике

так как , а интеграл последней функции за полупериод равен 0.

Коэффициент при второй гармонике

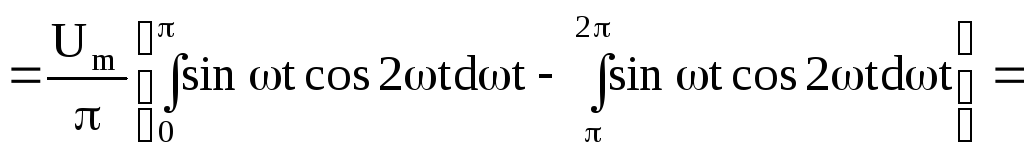
При =100В,=42,44В.

Таким образом,