Шпаргалка - 2000 / matan0006

1. Частной производной по х ф-ции z=f(x,y) в точке М(x,y) называется конечный предел отношения частного приращения _хZ к приращению х при стремлении х к нулю, если этот предел существует.

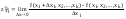. Частная производная 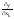есть мера скорости изменения у относительно х₁ при фиксированных значениях остальных независимых переменных. Каждая частная производная может быть найдена посредством диф-ния ф-ции f(x₁,x₂,…,x_k) по х_n, если остальные (k-1) независимые переменные рассматривать как постоянные параметры.

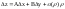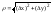2. Диф-мость ф-ции. Функция z = f(x, y) наз диф-мой в точке М(х, у), если в этой точке ее полное прира­щение представимо в виде , где и

Теорема 1 (о связи диф-мости и непрерывнос­ти). Если функция z = f(x, y) диф-ема в точке М(х, у), то она непрер в этой точке.

Теорема 2 (о связи диф-мости с существовани­ем частных производных). Если ф-ция z = f(x, y) диф-ма в точке М(х, у), то в этой точке она имеет частные произв по x и у, кот равны

4. Произв. слож. ф-ции. Если f(u₁,u₂,…,u_m) ф-ция многих переменных, а u_i=u(x₁,x₂,…,x_n) (i=1,2,…,m), то

(k=1,2,…,n)

5. Полная производная. Пусть ф-ции х=х(u), у=у(u) диф-мы в некоторой точке u, а функция z = f(x, y) диф-ма в соотв точке М(x, y). Тогда сложная функция z = f(x(u), у(u)), как функция одной переменной u, диф-ма в точке u и ее полная производная в этой точке вычисляется по формуле: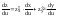

Следствие. Пусть ф-ция y=y(x) диф-ма в некоторой точке x, а функция z = f(x, y) диф-ма в соотв точке М(х, у). Тогда сложная функция z = f(x, y(x)), как ф-ция переменной x, диф-ма и ее полная производная в точке x вычисляется по формуле:

6. Полный диф-ал. Ф-ция y=f(x₁,x₂,…,x_n) имеет в точке (x₁,x₂,…,x_n) полный диф-ал, если ее приращение в этой точке может быть представлено в виде

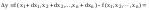
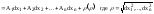и A₁,A₂,…A_n не зависят от dx₁,dx₂,…,dx_n. В этом случае полным диф-лом ф-ции f(x₁,x₂,…,x_n) называется выражение вида

7. Диф-ние функции заданной неявно уравнением F(x,y)=0. Если функция F(x, у) определена на не­котором множестве DR² и существует такая функция y=f(x), определенная на некотором множестве IR¹, что (х, f(x))D xI и выполняется равенство F(x,f(x)) 0 хI, то функция y=f(x) называется не­явной функцией, заданной уравнением F(x,y)=0.(1)

Теорема 1. Пусть функция у = f(x) задана неявно ур-ем (1), где F(x,y) диф-уема в точке (x₀,y₀), для которой .F(x₀,y₀)=0, и 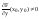. Пусть ф-ция у = f(x) диф-ма в точке x₀, тогда

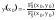
10. Производная по направлению. Производной ф-ции u=f(x,y,z) в точке P₀(x₀,y₀,z₀)D(f) по направлению вектора s называется конечный предел (если он сущ-ет) отношения приращения ф-ции к расстоянию |P₀P| при условии, что

РР₀, PD(f) и Р₀Рs.

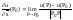
11. Градиентом ф-ции u=f(x,y,z) в точке P₀(x₀,y₀,z₀) наз. вектор, выч. по ф-ле:

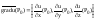
,s₀s и |s₀|=1

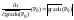, Вектор 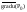направлен по нормали к поверхности уровня u(x,y,z)=c, где с = u(P₀) Произв. ф-ции u в точке Р₀ по направл вектора 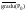принимает наиб. значение по сравнению с произв. ф-ции u в точке Р0 по любому др. направл. и это наиб. значение равно | |

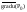12. Max(min) ф-ции нескольких переменных. Необходимые усл экстремума. Пусть ф-ция u=f(P) определена в точке Р₀ и имеет в ней экстремум. Тогда любая производная первого порядка ф-ции f в точке Р₀ равна нулю или не существует. Действительная ф-ция f(x₁,x₂,…,x_n), определенная при x_i=a_i, i=(1,n) имеет в точке (a1,…,an) max или min f(a1,…,an), если сущ такое положит число , что при всех x₁,x₂,…,x_n для которых выполняется неравенства 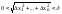и сущ значение , приращение ф-ции

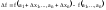
13. Двойной интеграл. Пусть z=f(P) определена в области DR². Разобьем D какими-нибудь линиями на n частей D₁,…,D_n, площади которых обозначим s1,…,sn, причем S_D=s₁+…+s_n, где S_D-площадь D. В каждой из областей Dk выберем произвольным образом точку Рк. Составим сумму: наз. двойной интегральной суммой для ф-ции z=f(P) в области D. d=max_(k=1,n)s_k – диаметр разбиения D на части. Если сущ конечн предел при d0 и этот предел не зависит ни от способа разбиения D на части, ни от выбора в них промежуточных точек, то этот предел наз. двойн интеграл.

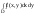. Д.И. численно равен объему вертикального цилиндрического тела построенного на основании D и ограниченного сверху соотв куском поверхности z=f(x,y)

16. Замена переменных в д.и. Пусть ф-ция z=f(x,y) интегрируема в области DR². Пусть ф-ции x=x(u,v), y=y(u,v) удовлетворяют условиям: 1. Определены в GR² и взаимно однозначно отображают G на D; 2. Непрерывно диф-мы в области G, причем якобиан 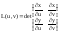либо отрицателен, либо не положителен в G. Тогда имеет место формула замены переменных в д.и. Полярная сист. коорд. Д.и. выражается через полярные коорд. фомулой 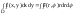где F(r,)-та ф-ция коорд r,, которая представляет данную ф-цию f(P) точки Р. Выражение rdrd наз. элементом площади в поляр коорд Оно эквив площади ABCD, где ADOA = rdr и AB=DC=dr.

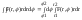
18. Кривол. Интегр. По коорд. Для данной спрямляемой дуги С, описываемой при atb уравне­ниями x=x(t), y=y(t), z=(t), кривол интеграл f(x, у, z)ds от огранич функции f(x,y,z) по опред равен

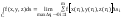
где

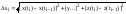
(a=t₀<t₁<…<t_m=b; t_i-1t_i i=1,2,…,m) если предел сущ кривол интеграл можно вычислить (или непосредственно определить) как интеграл по t: 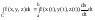где элемент дуги ds: Oпуская члены, относящиеся к z, получаем кривол интеграл для кривой, расположенной на плоско­сти Oxy. Он равен работе совершаемой при перемещении еденицы массы из А в В по Г в силовом поле F.

19. Ф-ла Грина. Пусть D – плоская область, ограниченная контуром С и пусть всюду в этой области непрерывны ф-ции Р и Q и их частные производные. Тогда справедлива ф-ла Грина:

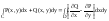
20. Условие независ. крив.инт. от пути интегриров. Пусть ф-ции Р(х,у), Q (х,y), а также их частные произв непрерывны в обл D ограниченной не­которой непрерывной замкнутой линией (не пересекающей себя). Возьмем в области D две фиксированные точки А(х₀,y₀), В(x₁,y₁) и будем рассматривать все возможные пути интегрирова­ния, ведущие из A в B и расположенные целиком в области D (таковы пути ALB, ANB на рис). Возможны два случая.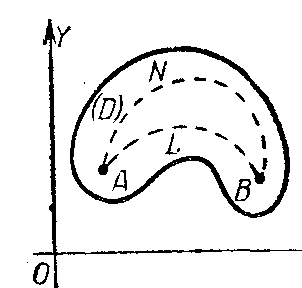

Случай 1 (исключительный). В области D тождест. удовлет. равенство 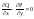(1). Тогда кривол интеграл не зависит от выбора пути, и соотв обознач Случай 2 (общий). Равенство (1) не является тожде­ством. Тогда кривол интеграл зависит от вы­бора пути. Пояснение. Разность I₁-I₂ кривол интегралов 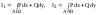равен сумме I₁+(-I₂). Последняя дает интеграл по контуру ALBNA, а он равен двойному интегралу разности частных производных по области ALBNA. Если ра­венство (1) есть тождество, I₃ = 0; значит, I₁=I₂, т. е. криволи­нейные интегралы вдоль путей ALB, ANB одинаковы. Если же равен­ство (1) не является тождеством, то можно по­добрать пути ALB и ANB так, чтобы I₃0 и тогда I₁I₂.

21. Ф-ция нескольких переменных. Ф-ция y=f(x₁,x₂,…,x_n) n переменных x₁,x₂,…,x_n относит упорядоченному множеству значений независимых переменных x₁,x₂,…,x_n значения зависимого переменного у. Множество Sx значений х, для которых определено соотношение f(x₁,x₂,…,x_n),есть область определения ф-ции. Линией уровня ф-ции нескольких переменных называется множество точек в Rn, в каждой из которых ф-ция f(x₁,x₂,…,x_n) принимает одно и то же знач. Если n<3, то говорят линии уровня, а n3 говорят поверхн уровня.

22. Предел ф-ции нескольких переменных. Ф-ция f(x₁,x₂,…,x_n) имеет (необходимо единственный) предел 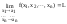, если для каждого положит числа сущ такая окрестность D точки (a₁, a₂,…,a_n), что для всех точек (x₁,x₂,…,x_n)D, исключая, быть может, точку (a₁, а₂,…,a_n), ф-ция f(x₁,x₂,…,x_n) опред и . При этом a₁,a₂,…,a_n могут быть как конечными, так и бесконечными.

23. Непрерывность. Ф-ция f(x₁,x₂,…,x_n) определ в некоторой окерстности () (a₁,a₂,…,a_n) непрерывна в точке (а₁,а₂,…,а_n) если сущ. предел f(x₁,x₂,…,x_n) при x₁a₁,…,x_na_n и этот предел равен f(а₁,а₂,…,а_n). Точка разрыва первого рода – это () а, в которой ф-ция разрывна и сущ. Пределы f(a+0) и f(a-0) не равные друг другу.

24. Произв. сложной ф-ции неск переменных. Если f(u₁,u₂,…,u_m) ф-ция многих переменных, а u_i=u(x₁,x₂,…,x_n) (i=1,2,…,m), то (k=1,2,…,n)

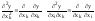
25. Частные произв высших порядков y=f(x₁,x₂,…,x_n) опред ф-лами: и.т.д. если соотв. пределы сущ.

26. Экстремум ф-ции неск перем. Необх условия. Если y=f(x₁,x₂,…,x_n) диф-ма в точке (a₁,a₂,…,a_n) то в точке (а₁,а₂,…,а_n) она имеет экстремум только тогда, когда ее частные производные по x₁,x₂,…,x_n равны нулю, при x₁=a₁,…,x_n=a_n.

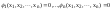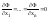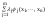27-28. Условный экстремум. Если есть дополн услов в виде m<n уравн связи (1) , то применяют следующие необх услов max/min ф-ции при огранич-ях (1): , где Ф(x₁,…,x_n)f(x₁,…,x_n)+ , где m параметров _i наз множителями Лагранжа. n+m неизвестных xi=ai и _i находят из m+n уравнений необх условий и уравн связи.

30. Сведение к повтор. Если контур области D встреч со всякой пересек его вертикальной прямой не более чем в двух точках M₁, M₂, то область D задается неравенст аxb, ₁(х)y₂(х) (а, b - крайние абсциссы области, ₁(х) и ₂(х) - функ­ции, выражающие ординаты нижней и верхней граничных линий AM₁B₁, AM₂B₂.

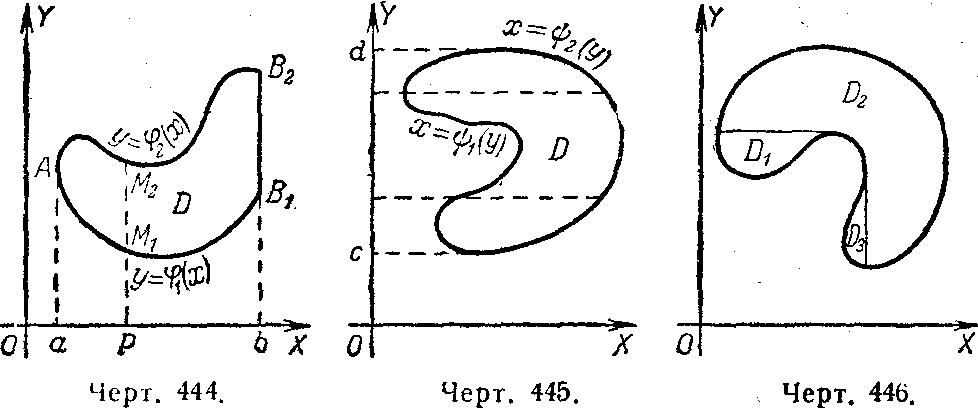
В этом случае двойной интеграл вычисляется по формуле 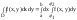или наоборот по гориз прямой.

32. Тройной интеграл. Пусть ф-ция f(x,у,z) точки Р(х,у,z) непрер внутри пространственной области D и на ее границе. Разобьем D на n частей; пусть v₁,…, v_n - их объемы. В каждой части возьмем по точке и составим сумму: S_n= f(x₁,у₁,z₁) v₁+… +f(x_n,у_n,z_n) v_n Предел, к кот S_n когда наибольший из диаметров частичных областей к нулю, наз тройным интегралом от функции f (х, у, z) no области D.

33. Криволин интеграл. -Нужно под-вить x=(x), y=(x) в выр выше. X,Y,Z –коорд.

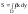
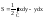
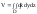
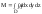где -плотность (ф-ция точки)