1.4.4. Логарифмически нормальное распределение

Существует целый класс распределений, которые можно отнести к нормальным, но при условии, что по нормальному закону распределена не сама величина t, а некоторая её функция. В логарифмически нормальном распределении по нормальному закону распределена не наблюдаемая величина t, а её логарифм . Логарифмически нормальное распределение широко применяется в теории надежности автоматизированных систем. Опыт показывает, что часто значения параметров в выборке, а также наработка на отказ стареющих элементов распределены по этому закону. Логарифмически нормальное распределение имеет место в том случае, когда скорость износа исследуемых объектов уменьшается во времени.

В случае имеем

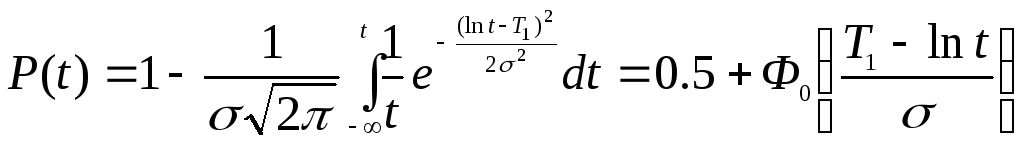, (1.30)

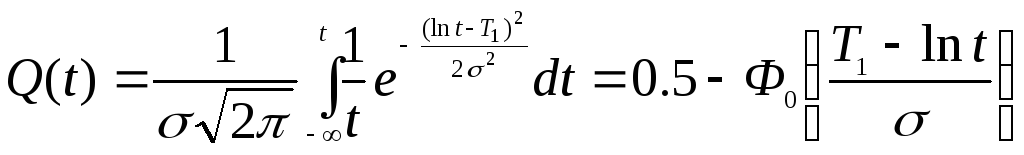, (1.31)

, (1.32)

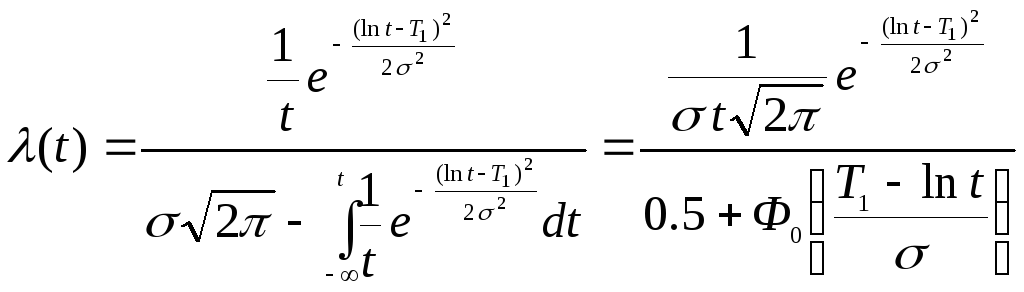, (1.33)

(1.34)

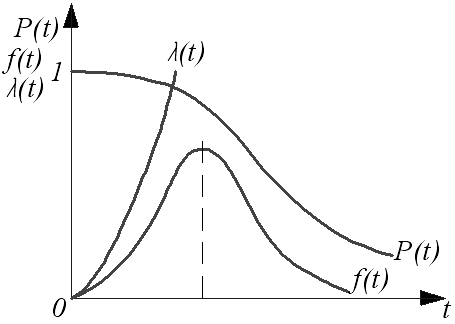
Графики, характеризующие логарифмически нормальное распределение, показаны на рис. 3 б.

a) б)

Р и с. 3. Графики изменения показателей надежности

а- нормальное распределение, б – логарифмически-нормальное распеределение

1.4.5. Распределение Вейбулла

Распределение Вейбулла необходимо, когда система содержит большое число объектов, слабо влияющих на работу друг друга. Распределение Вейбулла может быть применено для описания наработки до отказа ряда электронных и механических технических средств, включая период приработки.

Основные характеристики имеют следующий вид:

, (1.35)

, (1.36)

, (1.37)

, (1.38)

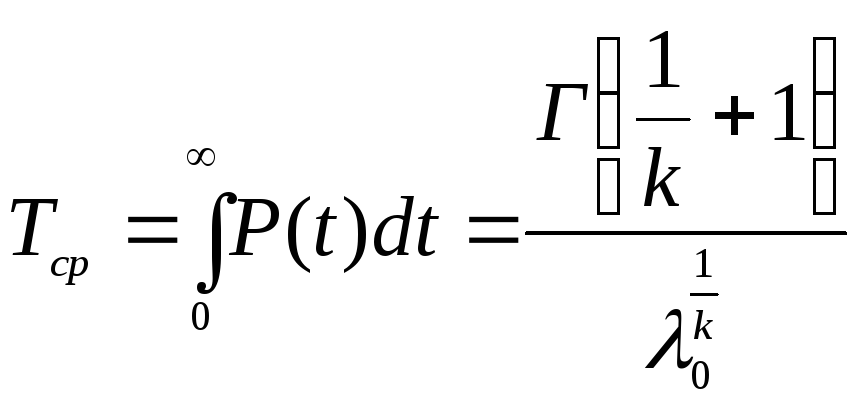, (1.39)

где Г – табулированная гамма-функция.

Графики, характеризующие распределение Вейбулла, показаны на рис. 4.

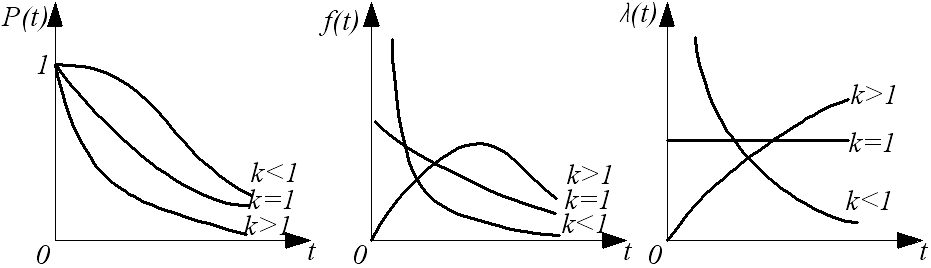
Р и с. 4. Графики изменения показателей надежности распределение Вейбулла

1.4.6. Гамма-распределение

При оценке надежности конструкций автоматизированных систем и качества технологических процессов часто используется модель накапливающихся повреждений, которая связана с гамма-распределением наработки на отказ.

Основные характеристики имеют следующий вид:

, (1.40)

, (1.41)

, (1.42)

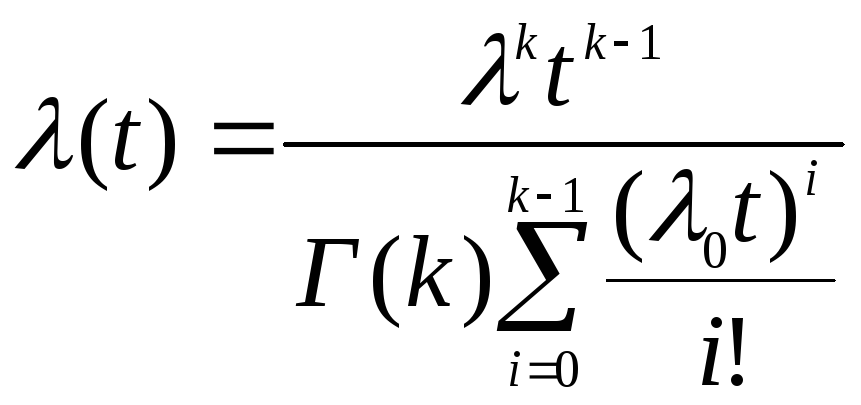, (1.43)

, (1.44)

где Г – табулированная гамма-функция. При целом k Г(k)=(k-1)!

Графики, характеризующие гамма-распределение, показаны на рис. 5.

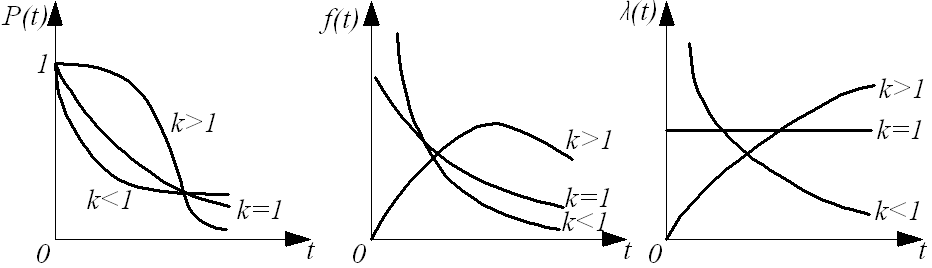
Р и с. 5. Графики изменения показателей надежности гамма-распределения

1.5. Показатели надежности восстанавливаемых объектов

Параметр потока отказов

По вероятностному определению параметра потока отказов:

, (1.45)

где - математическое ожидание числа отказов восстанавливаемого объекта за достаточ­но малую его наработку

По статистическому определению, параметр потока отказов есть отношение числа отказавших изделий в единицу времени к числу испытываемых изделий при условии, что все вышедшие из строя изделия заменяются исправными (новыми или отремонтированными):

, (1.46)

где – число отказавших образцов в интервале времени отдо ; – число испытываемых образцов;– интервал времени.

Параметр потока отказов и частота отказов для ординарных потоков с ограниченным последействием связаны интегральным уравнением Вольтера второго рода:

(1.47)

По известной можно найти все количественные характеристики надежности невосстанавливаемых изделий. Поэтому (1.47) является основным уравнением, связывающим количественные характеристики надежности невосстанавливаемых и восстанавливаемых изделий при мгновенном восстановлении.

Наработка на отказ

Эта характеристика определяется по статистическим данным об отказах по формуле:

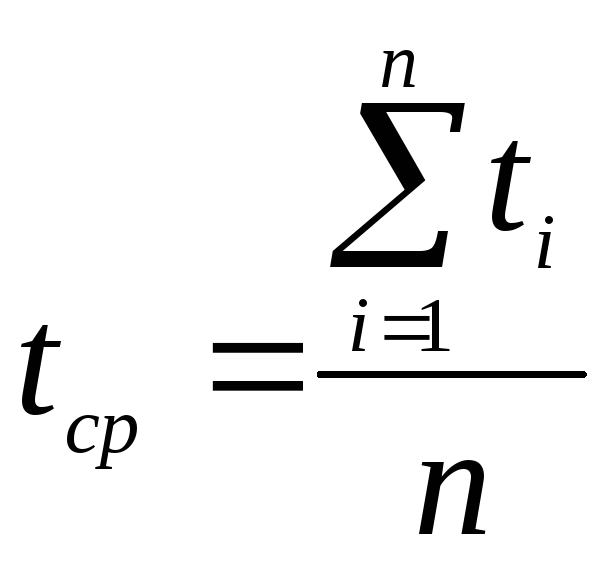(1.48)

где – время исправной работы изделия между -м и -мотказами; –число отказов за некоторое время

Из формулы (1.48) видно, что в данном случае наработка на отказ определяется по данным испытания одного образца изделия. Если на испытании находится N образцов в течение времени t, то наработка на отказ вычисляется по формуле

, (1.49)

где – время исправной работыj-го образца изделия между -м и -мотказами; –число отказов за некоторое время j-го образца.

Наработка на отказ является достаточно наглядной характеристикой надежности, поэтому она получила ши­рокое распространение на практике.

Параметр потока отказов и наработка на отказ ха­рактеризуют надежность ремонтируемого изделия и не учитывают времени, потребного на его восстановление. Поэтому они не характеризуют готовности изделия к выполнению своих функций в нужное время. Для этой це­ли вводятся такие критерии, как коэффициент готовности и коэффициент вынужденного простоя.

Коэффициентом готовности

Коэффициентом готовности называется отношение времени исправной работы к сумме времен исправной работы и вынужденных простоев изделия, взятых за один и тот же календарный срок:

, (1.50)

где – суммарное время исправной работы изделия;– суммарное время вынужденного простоя.

Время ивычисляются по формулам:

, (1.51)

где – время работы изделия между -м и -мотказами; – время вынужденного простоя после -гоотказа; –число отказов(ремонтов) изделия.

Выражение (1.50) является статистическим определением коэффициента готовности. Для перехода к вероятностной трактовке величины изаменяются математическими ожиданиями времени между соседними отказами и времени восстановления соответственно.

Тогда

, (1.52)

где – наработка на отказ;– среднее время восстановления.

Коэффициентом вынужденного простоя называется отношение времени вынужденного простоя к сумме времен исправной работы и вынужденных простоев изделия, взятых за один и тот же календарный срок.

Согласно определению:

(1.53)

или переходя к средним величинам

(1.54)

Коэффициент готовности и коэффициент вынужденного простоя связаны между собой соотношением:

(1.55)

В некоторых случаях критериями надежности восста­навливаемых систем могут быть также критерии надеж­ности невосстанавливаемых систем, например: вероят­ность безотказной работы, частота отказов, средняя на­работка до первого отказа, интенсивность отказов. Такая необходимость возникает всегда, когда имеет смысл оце­нить надежность восстанавливаемой системы до первого отказа, а также в случае, когда применяется резервиро­вание с восстановлением отказавших резервных устройств в процессе работы системы, причем отказ всей резерви­рованной системы не допускается.