11. Формулировка уравнения Шредингера для молекулярного иона водорода (Н2)+.

Оператор Гамильтона состоит из двух частей – оператора кинетической энергии () и оператора потенциальной энергии (). Первый представляет собой оператор Лапласа (в атомных единицах), второй в случае атома водорода выражается в соответствии с законом Кулона в виде 1/r (также в атомных единицах):

Так как атом водорода обладает сферической симметрией, то для решения уравнения необходимо перейти к сферическим координатам (рис. 2.1):

x = r sin θ cos φ;

y = r sin θ sin φ;

z = r cos θ;

0 ≤ r < ∞; 0 ≤ θ ≤ π; 0 ≤ φ ≤ 2π.

Р и с. 2.1. Связь сферических координат с декартовыми

При решении уравнения Шрёдингера (1.1) в сферических координатах переменные (r, θ, φ) легко разделяются, что приводит к следующим функциям для атома водорода:

где – радиальная часть функции,– часть функции, зависящая только от угловых переменных (сферическая гармоника),N – нормировочный множитель.

Радиальная часть функции имеет вид

где – присоединенный полином Лагерра степени (n+l), порядка (2l+1). Полиномы Лагерра с различными n и l ортогональны между собой, что определяет ортогональность радиальных функций.

Сферическая гармоника является произведением угловых функций Θ(θ) и Φ(φ):

где – присоединенный полином Лежандра степени l, порядка |m|.

Нормировочный множитель определяется квантовыми числами n, l, m (n = 1, 2, 3, …; l = 0, 1, 2, …, (n-1); |m| = 0, 1, 2, …, l ):

Число n называется главным квантовым, и оно определяет энергию атома водорода (или водородоподобного атома).

Квантовое число l называется орбитальным. Оно определяет величину углового момента и, следовательно, форму орбиталей, которые обозначаются латинскими буквами: s (l = 0), p (l = 1), d (l = 2), f (l = 3), g (l = 4). Буквенные обозначения связаны с английскими названиями спектральных линий в атомных спектрах: sharp (резкий), principal (главный), diffuse (диффузный), fundamental (основной).

Квантовое число m характеризует значение проекции углового момента на выбранную ось. В конкретном физическом эксперименте такая ось задаётся направлением электрического или магнитного поля.

Функции с главным квантовым числом до 2 для атома водорода представлены в табл. 2.1, а для водородоподобного атома – в табл. 2.2.

Таблица 2.1

Функции (орбитали) атома водорода (ρ = r / a₀ , где a₀ – боровский радиус)

Таблица 2.2

Функции водородоподобного атома (ρ = z r / a₀ , где z – заряд ядра)

n l m	Обозначение	Ψnlm
1 0 0	1s
2 0 0	2s
2 1 0	2pz
2 1 1	2py
2 1-1	2pz

Радиальные части s- и p-функций можно представить в виде следующих графиков (рис. 2.2).

Р и с. 2.2. Радиальные функции водородоподобного атома

12. Нерелятивистское приближение, границы его применимости. Влияние релятивистских поправок на рассчитываемые атомные и молекулярные свойства. (формулы в лекциях) В атомной системе единиц скорость движения электрона в молекуле приблизительно равна заряду ядра. В атомной системе единиц скорость света равна 127 или обратной величине тонкой структуры. Поэтому если заряд ядра = 127, то электрон должен двигаться со скоростью света, но это не возможно. В атоме водорода электрон движется 1% от скорости света; и с ростом заряда ядра скорость электрона приближается к световой. При этом масса электрона заметно увеличивается.

Этот эффект заметен для элементов 3 периода, он существенен для элементов 4 периода и обязательно учитывать для элементов 5 периода. Особенно сильно растет масса 1s электрона, т.е. близко к ядру. При этом 1s орбиталь сжимается. Вышележащие s орбитали также сжимаются, чтобы сохранилась ортогональность м/у ними.

Сжатые s орбитали лучше экранируют ядра, что приводит к увеличению орбитали с большим угловым моментом. Но р-орбитали не увеличиваются из-за sр - орбитальных взаимодействий. Увеличивается d и f орбитали. При увеличении d и f проявляются химические свойства тяжелых металлов. Способны к образованию дельта связи. Корреляция массы электрона = 4% . Уравнение Шрёдингера не применимо для решения релятивистских задач; потому что присутствие 2 производных для координат и 1 по времени т.к. имеют разный порядок , это уравнение не подчиняется преобразованиям Уоленса. Преобразование Уоленса – это преобразование перехода из 1 системы координат в другую. Для преобразования релятивистских задач используют уравнение Дирака. При решении уравнения Дирака возникают отрицательные энергетические состояния, соответствующие ненулевой вероятности превращения электрона в позитрон. Релятивистские эффекты мало влияют на длины связей, валентные углы и энергию атомизации.

Релятивистские эффекты проявляются в плоскости и не проявляются для валентных электронов. Поэтому при решении химических задач релятивистские поправки можно считать константой. Релятивистские поправки, как правило, меньше, чем ошибки связанные: 1. С использованием ограниченного базисного набора.

2. С приближением электронной корреляции.

13. Приближение Борна-Оппенгеймера. Адиабатическое приближение. Неадибатическое решение стационарного уравнения Шредингера. Границы применимости адиабатического приближения.

Оба эти приближения основаны на том, что масса ядер примерно в тысячи раз больше массы электрона. Электроны движутся с высокой скоростью около 1% от скорости света. Поэтому можно считать, что электрон движется в поле покоящихся ядер. В этом заключается смысл приближений. ( формулы лекций). Допустим, известно решение электронного уравнения Шредингера. параметры задаются до начала решения уравнения. Поскольку оператор Гамильтона эрмитов, то мы выбираем решение электронного уравнения Шредингера ввиде ортонормированных электронноволновых функций.

(формулки тут всякие) для того, чтобы упростить полученные уравнения мы используем свойство ортонормальности электроноволновых функций.

Переходим к интегралам умножая слева на житую электронную функцию и интегрируем…( еще куча формулок) Приближение Борна-Оппенгеймера заключается в приближении элементами не адиабатического приближения 1,2 порядка. (формулки) Не адиабатические элементы ответственны за преобразование типа электронноволновой функции при изменении ядерных координат. Адиабатическое приближение и приближение Оппенгеймера не применимо в том случае, если при изменении ядерной конфигурации меняется тип конфигурации. Ядерные параметры становятся переменными. В адиабатическом приближении остается 1 не адиабатический элемент 2 порядка для i=j. Этот вклад называется диогональной коллекцией (формулка). Чаще всего приближение Борна – Оппенгеймера не применимо к фотохимическим реакциям и иногда не применимо к реакциям сопровождающимся гомолитическими разрывами связи. (реакция) молекула LiF полярна и описывается ввиде 2 суперпозиций 2-х волновых функций полярной и неполярной. Энергия полярной меньше энергии неполярной, но полярная молекула диссоциирует на атомы.

Изолированные атомы устойчивее ионов. Для разделенных Li и F энергия ионноволновой функции больше чем энергия неполярной волновой функции.

Р и с. 3.2. Кривые диссоциации молекулы Li-F

В области пересечения приближения Оппенгеймера неприменимо. После принятия приближения Борна – Оппенгеймера молекулярное уравнение Шредингера распадается на 2 уравнения ( формулки) .

Сначало решают электронное уравнение Шредингера при заданных координатах ядер. Координаты ядер можно задать 2 способами. Далее оптимизируют геометрию с целью поиска минимума эл. Энергии.

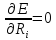
Далее решают ядерное уравнение Шредингера. Из найденной ядерно-волновой функции вычисляются колебательные и вращательные уровни Е.

Эти результаты помогают вычислить ИК спектры, микроволновые спектры, комбинационно рассеянные (Романовские).

Решение ядерного уравнения позволяет вычислить энергию нулевых колебаний ядер, а также энергию колебательную, поступательную и вращательную движения молекулы в целом. Эти 4 вклада необходимы для вычисления энергетического характера молекул при стандартных условиях.

Классификация движений молекул позволяет вычислить как энтропию, так и энтальпию энергетических молекул. Зная энтропию, можно узнать энегрия Гиббса. Е _эл. (типа стрелочка вправо) ΔЕ, G°( тоже стрелка) ΔG°.

ΔЕ практически ΔG°

14. Орбитальная модель. Электронный оператор Гамильтона. Одноэлектронный гамильтониан и оператор электронного отталкивания. Понятия "орбиталь", "спин-орбиталь". Спин-орбитальный детерминант (детерминант Слэйтера). Полная формулировка орбитальной модели.

Орбитальная модель –графическое изображение распределения плотности заряда электрона в атоме… Обоснование орбитальной модели атома, исходящее из корпускулярного характера электрона, состоит в следующем. Вероятность определенного положения электрона внутри объема пространства, окружающего атомное ядро, весьма велика, так как рассматривается устойчивое ( реально существующее) состояние атома. Такое распределение следует понимать так, что на любом выбранном расстоянии от ядра вероятность пребывания электрона одинакова во всех направлениях радиуса-вектора. Как следует из рис. 9, вероятность пребывания электрона в атомном ядре равна нулю, она незначительна вблизи ядра, но быстро возрастает при удалении от ядра. На некотором расстоянии ( для атома водорода оно равно. Бора) вероятность достигает максимума, а затем, медленно уменьшается, асимптотически приближаясь к нулю на расстоянии, стремящемся к бесконечности

Электронный оператор Гамильтона-(Оператор набла ∇ )– это символический вектор, сочетающий в себе векторные и дифференцирующие свойства.

,

Более близкие к истинным решения получают с помощью метода самосогласованного поля (ССП), предложенного Хартри. В методе ССП межэлектронным отталкиванием не пренебрегают, но действие на данный электрон всех остальных электронов заменяют средним полем, приближенно воспроизводящим их суммарное действие; последнее зависит от координат только рассматриваемого электрона. Это дает возможность разделить в сферической системе координат переменные в уравнении Шредингера. С формальной точки зрения это достигается следующим образом. Одноэлектронный гамильтониан записывают в виде: http://quant.distant.ru/files/Atom/Atom_razd.pdf(со стр 8 формулы) Последнее слагаемое описывает отталкивание между электронами i и j, усредненное по всем положениям электрона j и, следовательно, зависящее только от координат электрона i . Последствия этого состоят в следующем.

Рассмотрим гамильтониан ( формула) Его собственные функции (функции Хартри) имеют вид орбитальных произведений: ( формула) Собственные значения Н представляются суммой собственных значений h _i^ССП: ( опять долбанная формула) Энергия ε_i есть сумма кинетической энергии i-го электрона, потенциальной энергии его притяжения к ядру и средней потенциальной энергии его отталкивания от остальных электронов. Следовательно, Е` есть сумма кинетической энергии всех электронов, потенциальной энергии их притяжения к ядру и удвоенной потенциальной энергии их усредненного отталкивания от остальных электронов. Удвоение возникло потому, что отталкивание между электронами i и j учтено дважды: как среднее по j в h_i^ССП и среднее по i в h_j^ССП. С учетом этого, полная энергия атома равна: ( формулы) Соответственно, гамильтониан атома должен иметь вид: (формулы) Таким образом, необходимо решить систему одноэлектронных уравнений с гамильтонианом (45), включающим усредненное межэлектронное взаимодействие – систему уравнений Хартри. Для этого нужно построить набор операторов h_i^ССП для чего следует прежде рассчитать усредненные величины (формул). Значит, отталкивание электрона i, усредненное по всем положениям электрона j, равно: (формула)

Однако, чтобы вычислить этот интеграл, волновые функции χ _j (r_j) должны уже быть известны! Этопротиворечие преодолевается следующим образом. Сначала задаются некоторым набором N одноэлектронных функций, максимально близких к правильным χ _j ⁰(r_j) (позже мы увидим, что сделать это легко). С их помощью вычисляют интеграл (46) и строят оператор (h_i⁰)^ССП. Затем решают набор одноэлектронных уравнений Хартри, возникающий из условия минимума среднего значения гамильтониана (40), вычисляемого с волновой функцией Хартри (42): ( формула) Полученные решения χ _j ¹(r_j) используют, чтобы построить "исправленный" оператор (h_i¹)^ССП , вновь решают ту же систему уравнений, но теперь – с (h_i¹)^ССП и т.д. – до тех пор, пока получаемые собственные значения уравнений Хартри (т.е. энергии состояний)будут отличаться от полученных на предыдущей итерации лишь на очень незначительную величину (~ 10^-6 а.е.)Этот процесс называется самосогласованием, а результирующее поле, создающее усредненный потенциал в (40), называется самосогласованным полем – отсюда и название метода. ( хз то ли вообще, другого не нашла)

ОРБИТАЛЬ – область наиболее вероятного местонахождения электрона в атоме (атомная орбиталь) или в молекуле (молекулярная орбиталь).

Спин-орбиталь — это одноэлектронная волновая функция, получаемая из орбитали умножением ее на «спин-функцию», описывающую спиновое состояние отдельного электрона.

Детерминант Слейтера – детерминант, построенный из ортонормированных спин-орбиталей - атомных или молекулярных. Позволяет получить приближенную многоэлектронную волновую функцию N электронов, обеспечивая ее правильные антисимметричные свойства. Элементы детерминанта Слейтера есть описывающие электроны орбитали и перестановка электронов эквивалентна перестановке местами столбцов (строк) детерминанта, что изменяет его знак:

   

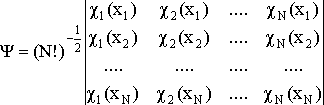
Детерминант Слейтера является единственной функцией, обеспечивающей антисимметричность волновой функции, записанной через орбитали (орбитальное приближение). Следовательно, он дает только одно решение соответствующих одноэлектронных уравнений. Хотя электроны неразличимы, в орбитальном приближении каждый электрон описывается "своей" волновой функцией. Системы, в которых все электроны занимают орбитали попарно, называются системами с закрытыми (замкнутыми) электронными оболочками. Для таких систем детерминант Слейтера состоит из дважды занятых электронами орбиталей, число которых равно половине числа электронов. Системы с нечетным числом электронов называются системами с открытыми (незамкнутыми) оболочками.

Наиболее полная формулировка орбитальной модели такова: волновая функция многоэлектронной системы может быть представлена ввиде линейной комбинации функций Ф_k ( k=1,2,…М)

Каждая функция Ф_k особым образом построена из множества (набора) спин-орбиталей ψ(r, ϭ). Каждая из спин-орбиталей представляет из себя произведение : ψ(r, ϭ)=φ(r) * η(ϭ).

Одной из орбиталей φ(r), входящих в исходный набор ортонормированных функций φ_i(r), i=1,2…,К., и одной из двух ортонормированных спиновых функций η_i(ϭ), i=1,2.