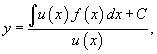Вопрос 9.

Дифференциа́льное уравне́ние — уравнение, связывающее значение производной функции с самой функцией, значениями независимой переменной, числами (параметрами). Порядок входящих в уравнение производных может быть различен (формально он ничем не ограничен). Производные, функции, независимые переменные и параметры могут входить в уравнение в различных комбинациях или все, кроме хотя бы одной производной, отсутствовать вовсе. Дифференциальное уравнение порядка выше первого можно преобразовать в систему уравнений первого порядка, в которой число уравнений равно порядку исходного уравнения.

Теорема существования единственного решения - ??

Вопрос 10.

Уравнением с разделенными переменными называется дифференциальное уравнение вида

f(x)dx + g(y)dy = 0

с непрерывными функциями f(х) и g(y).

Равенство

где C — произвольная постоянная, определяет общий интеграл уравнения с разделёнными переменными.

Начальное условие для уравнения  f(x)dx + g(y)dy = 0 можно задавать в виде y(x₀) = y₀ или в виде x(y₀) = x₀ .

 

Уравнением с разделяющимися переменными называется дифференциальное уравнение вида 

f₁(x)g₁ (y)dx + f₂(x) g₂(y)dy =0 .

Функции f₁(x), g₁(y), f₂(x), g₂(y) непрерывны в cвоих областях определения и g₁(y)f₂(x) ≠ 0 .

 

Разделив обе части уравнения на отличное от нуля произведение g₁(y)f₂(x), получим уравнение с разделенными переменными

Общий интеграл этого уравнения имеет вид

Вопрос 11.

Линейные дифференциальные уравнения первого порядка

Определение линейного уравнения первого порядка

Дифференциальное уравнение вида

где a(x) иb(x) − непрерывные функцииx, называтсялинейным неоднородным дифференциальным уравнением первого порядка. Мы рассмотрим два метода решения указанных уравнений:

• Использование интегрирующего множителя;

• Метод вариации постоянной.

Использование интегрирующего множителя

Если линейное дифференциальное уравнение записано в стандартной форме:

то интегрирующий множитель определяется формулой:

Умножение левой части уравнения на интегрирующий множитель u(x) преобразует ее в производную произведенияy(x)u(x).  Общее решение дифференциального уравнения выражается в виде:

где C− произвольная постоянная.

Решить уравнение  y' − y − xe^x = 0.

Решение.

Запишем данное уравнение в стандартной форме:

      

Будем решать это уравнение, используя интегрирующий множитель:

      

Тогда общее решение линейного дифференциального уравнения определяется выражением:

      

 Уравнение Бернулли

Уравнение Бернуллиявляется одним из наиболее известныхнелинейных дифференциальных уравнений первого порядка. Оно записывается в виде

где a(x) иb(x) − непрерывные функции.  Еслиm= 0, то уравнение Бернулли становитсялинейным дифференциальным уравнением. В случае когдаm= 1, уравнение преобразуется вуравнение с разделяющимися переменными.  В общем случае, когдаm≠ 0, 1, уравнение Бернулли сводится к линейному дифференциальному уравнению с помощью подстановки

Новое дифференциальное уравнение для функции z(x) имеет вид

и может быть решено способами, описанными на странице Линейные дифференциальные уравнения первого порядка.

   Пример 1

Найти общее решение уравнения  y' − y = y²e^x.

Решение.

Для заданного уравнения Бернулли m= 2, поэтому сделаем подстановку

      

Дифференцируя обе части уравнения (переменная yпри этом рассматривается как сложная функцияx), можно записать:

      

Разделим обе части исходного дифференциального уравнения на y²:

      

Подставляя zиz', находим:

      

Мы получили линейное уравнение для функции z(x). Решим его с помощью интегрирующего множителя:

      

Общее решение линейного уравнения выражается формулой

      

Возвращаясь к функции y(x), получаем ответ в неявной форме:

      

который можно записать также в виде:

      

Заметим, что при делении уравнения на y²мы потеряли решениеy= 0. В результате, полный ответ записывается в виде: