
ЧМТФ Лабораторная работа 5
.docxЛабораторная работа 5.
Нелинейные одномерные колебания
Цель работы: изучение нелинейных колебаний маятника с учетом сил сопротивления.
Теоретические сведения . Вывод дифференциального уравнения колебания математического маятника
Рассмотрим
колебания математического маятника
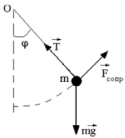
относительно точки подвеса О
(рис.
5.1). Момент инерции материальной точки
массы m
обозначим
J,
длину
нити L.
Тогда в данном случае
 .
Положение тела будем характеризовать
углом отклонением от положения
равновесия
.
Положение тела будем характеризовать
углом отклонением от положения
равновесия .
Движение тела описывается основным
уравнением динамики вращательного
движения
.
Движение тела описывается основным
уравнением динамики вращательного
движения
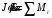 ,
где
,
где
 –
сумма
–
сумма
|
|
|
Рисунок 6.1. |
(с
учетом знака проекций) моментов всех
сил относительно точки подвеса О,
действующих на материальную точку m,
 -
угловое ускорение. Момент силы тяжести
-
угловое ускорение. Момент силы тяжести
 ,
сила сопротивления
среды
,
сила сопротивления
среды
 ,
где k
-коэффициент
сопротивления, V
- скорость.
Линейная скорость связана с угловой по
формуле
,
где k
-коэффициент
сопротивления, V
- скорость.
Линейная скорость связана с угловой по
формуле
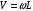 ,
поэтому момент силы сопротивления
,
поэтому момент силы сопротивления
 .
Момент силы натяжения нити T
равен нулю. Таким образом основное
уравнение динамики вращательного
движения принимает вид
.
Момент силы натяжения нити T
равен нулю. Таким образом основное
уравнение динамики вращательного
движения принимает вид
|
|
(5.1) |
или
 .
.
Порядок выполнения работы
Задание 1. Изучение колебаний маятника с учётом трения.
Найти
зависимость угла отклонения
 математического
маятника от положения равновесия при
различных значениях коэффициента трения
k
(0,
0.05 кг/с, 0.2 кг/с и 1 кг/с). Расчеты произвести
до
математического
маятника от положения равновесия при
различных значениях коэффициента трения
k
(0,
0.05 кг/с, 0.2 кг/с и 1 кг/с). Расчеты произвести
до
 с.
Начальное положение
с.
Начальное положение
 ,
начальная скорость - нулевая. Данные
для расчетов представлены в табл. 5.1.
,
начальная скорость - нулевая. Данные
для расчетов представлены в табл. 5.1.
|
|
|
Таблица 5.1 |
Задание 2. Построение фазовых диаграмм математического маятника.
Построить
фазовые диаграммы (зависимости
 )
для рассмотренных выше маятников.
Построить фазовые диаграммы при нулевом
начальном угле и различных начальных
скоростях без трения и с трением.
Рассмотреть случаи переворотов. Сделать
выводы о виде фазовых диаграмм в
зависимости от параметров системы и
начальных условий.
)
для рассмотренных выше маятников.
Построить фазовые диаграммы при нулевом
начальном угле и различных начальных
скоростях без трения и с трением.
Рассмотреть случаи переворотов. Сделать
выводы о виде фазовых диаграмм в
зависимости от параметров системы и
начальных условий.
Задание 3. Нахождение зависимости периода колебаний от коэффициента трения и амплитуды колебаний.
Вычислить периоды колебаний при различных значениях коэффициента трения и начального отклонения. Результаты занести в табл. 5.2.
|
|
|
|
|
Таблица 5.2 |
Задание 4. Изучение вынужденных колебаний.
Добавить
в правую часть дифференциального
уравнения (5.1) дополнительное слагаемое
 - угловое ускорение, вызванное внешней
вынуждающей силой. Найти зависимость
угла отклонения
- угловое ускорение, вызванное внешней
вынуждающей силой. Найти зависимость
угла отклонения
 математического
маятника от положения равновесия при
различных значениях частоты
математического
маятника от положения равновесия при
различных значениях частоты
 вынуждающей силы (
вынуждающей силы ( ,
,
 ,
,
 ,
,
 ,
где
,
где
 - малая величина Принять
коэффициент трения и начальные условия
равными нулю, а также А
=
1 рад/с .
- малая величина Принять
коэффициент трения и начальные условия
равными нулю, а также А
=
1 рад/с .
Задание 5.
Построить
резонансные кривые (зависимости
 при различных коэффициентах сопротивления.
при различных коэффициентах сопротивления.
Контрольные вопросы.
-
Выведите дифференциальное уравнение колебаний математического маятника.
-
Объясните метод решения дифференциального уравнения, применяемый при выполнении данной работы.
-
Объясните метод нахождения периода колебаний с помощью компьютерного моделирования.
-
Чему равен период математического маятника теоретически? В каких случаях результаты, вычисленные по этой формуле, опровергаются компьютерным моделированием?
-
Как зависит период колебаний от амплитуды?
-
Объясните, почему период нелинейных колебаний не является постоянной величиной.
7. Что такое фазовая диаграмма и как она выглядит?
8. Что такое резонанс колебательной системы?

 ,
,

