ЧМТФ Лабораторная работа 4

Лабораторная работа 4.

Моделирование законов динамики.

Цель работы:

• познакомиться с практическим применением законов Ньютона для реше­ния задач динамики методами компьютерного моделирования;

• научиться решать дифференциальные уравнения с помощью системы MathCAD.

Методы решений дифференциальных уравнений

Дифференциальным называется уравнение, которое, кроме независимых переменных и неизвестных функций этих переменных, содержит еще и производные неизвестных функций. Наивысший порядок производных неизвестной функции, входящих в это уравнение, называется порядком дифференциального уравнения.

Пример 1. Груз массой кг (рис. 4.1), получив в точке А начальную скорость 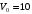м/с, движется в наклонной трубе АВ, расположенной в вертикальной плоскости. На груз кроме силы тяжести действует постоянная сила Н и сила сопротивления среды , где кг/м. Длина трубы м. Коэффициент трения скольжения груза о стенки трубы Считая груз материальной точкой, найти время движения, зависимости скорости и координаты от времени, а также скорость в точке В.

Рисунок 4.1.

Решение.

При решении данной задачи на начальном этапе воспользуемся обычным алгоритмом решения задач на динамику материальной точки:

1. Расставим на рисунке 4.1 силы, действующие на тело, и запишем второй закон Ньютона в векторном виде: .

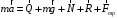2. Выберем оси координат OX и OY таким образом, чтобы большинство сил были параллельны или перпендикулярны осям.

3. Запишем второй закон Ньютона в проекциях на координатные оси:

ось OX: ,

ось OY: .

4. Учитывая, что сила трения скольжения равна произведению коэффициента трения на силу реакции опоры, получим выражение для определения ускорения . Полученная формула показывает, что ускорение не является постоянной величиной, поэтому в данном случае нельзя пользоваться известными формулами для вычисления скорости и перемещения при равноускоренном движении. Так как скорость является первой производной от координаты по времени, а ускорение - второй производной, то мы имеем дифференциальное уравнение второго порядка.

Метод Эйлера для решения дифференциальных уравнений.

Координата частицы x и ее скорость V определяются уравнениями

.

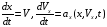Задача состоит в вычислении зависимостей и при условии, что заданы начальные значения координаты и скорости .

Выберем достаточно малое конечное значение величины , а затем воспользуемся соотношениями:

,

.

Многократно применяя эти соотношения, можно рассчитать значения x и V в ряде дискретных, но достаточно близких друг к другу точек.

Алгоритм решения:

1. Ввод данных

2. вводится точность решения задачи (максимальное время расчета, шаг по времени и количество малых промежутков времени, на которых производится расчет). Очень важно выбрать правильный шаг по времени . Чем меньше , тем точнее результат, но при этом увеличивается машинное время для проведения расчетов.

3. Ввод начальных условий.

4. На каждом малом промежутке времени вычисляется новое значение скорости и координаты. Если рассматривать движение в достаточно малый промежуток времени, движение можно считать равноускоренным. В пакете MathCAD имеются два различных оператора, с помощью которых можно запрограммировать повторяющиеся фрагменты программ. Программа расчета с помощью оператора цикла (прямого перебора) for приведена в процедуре Eulerl на рисунке 4.2.

Рисунок 4.2.

В процедуре Euler2 на рисунке 4.3 приведена программа расчета с помощью оператора цикла while с предварительной проверкой условия.

Рисунок 4.3

Для построения зависимостей скорости и координаты от времени необходимо рассчитанные значения физических величин занести в таблицу, которую назовем матрицей значений М. В нулевой столбец матрицы будем заносить значения времени, в первый - скорости, во второй - координаты. В процедуре Euler3 на рисунке 4.4 приведена программа создания матрицы значений для построения графических зависимостей. Также на рисунке представлен результат в виде таблицы значений времени, скорости, координаты.

Рисунок 4.4

Выделим массивы времени скорости, координаты.

Построим нужные графики.

Рисунок 4.5

Использование встроенных функций пакета Mathcad

для численного решения дифференциальных уравнений

Для решения дифференциальных уравнений в численном виде пользователям MathCAD предлагается ряд удобных процедур. Для быстрого получения практического результата удобно пользоваться процедурой Odesolve. В большинстве ситуаций дифференциальное уравнение или система дифференциальных уравнений могут быть решены с помощью этой процедуры, причем сам процесс достаточно прост. Обычно этот метод применяется, если известно время движения тела. Общий принцип работы с процедурой Odesolve состоит в следующем. В рамках блока Given задается решаемое уравнение (или система уравнений) с начальными условиями. Заканчивается блок командой вызова Odesolve с соответствующими аргументами. Таким образом, в численном виде определяется искомая функциональная зависимость (или зависимости).

Для решения нашей задачи рассмотрим уравнение .

Рисунок 4.6

На рисунке 4.6 число 0.931 обозначает время движения груза, которое вычислено методом Эйлера. Компьютер автоматически подбирает шаг интегрирования наиболее оптимальным способом.

Для ввода производных в уравнениях следует использовать штрих (комбинация клавиш Ctrl+F7) или кнопку производных панели Calculus. При вводе производных в начальных условиях следует использовать только комбинацию клавиш Ctrl+F7. При вводе уравнений после имени функции в скобках обязательно должен быть указан аргумент. Ввод знака « = » осуществляется с помощью комбинации клавиш Ctrl + = или с помощью оператора =, расположенного на панели инструментов Boolean (логика). Зависимость координаты от времени, вычисленная с помощью метода встроенных функций приведена на рисунке 4.7. Шаг по времени, который приведен на рисунке 4.7, необходим для построения графика и ничем не связан с шагом для решения дифференциального уравнения.

Рисунок 4.7

Рассмотренное выше дифференциальное уравнение второго порядка можно представить так же, как систему двух дифференциальных уравнений первого порядка (рисунок 4.8). В этом случае можно получить функциональную зависимость скорости от времени (рисунок 4.9).

Рисунок 4.8

Рисунок 4.9

Рассмотрим еще один способом решения дифференциальных уравнений с помощью процедуры rkfixed. В качестве примера решим задачу о гармоническом осцилляторе. Дифференциальное уравнение второго порядка преобразуем к системе из двух дифференциальных уравнений первого порядка

Зададим начальные условия , соответствует начальной координате, а – начальной скорости. Зададим теперь матрицу D. С учетом того, что искомая величина соответствует нулевому элементу массива, ее первая производная – первому, а вторая – второму, имеем .

Далее используется процедура rkfixed(y, x1, x2, N, D), где y – матрица начальных условий, х1 и х2 – интервал интегрирования, N – количество точек, на которое разбивается интервал интегрирования. Результатом выполнения процедуры rkfixed является массив, в первом столбце которого находится аргумент функции, во втором – сама функция, в третьем- ее первая производная и т.д. На рисунке 4.10 представлено решение задачи о гармоническом осцилляторе, у которого масса и частота равны 1 с начальной координатой равной 0 и начальной скоростью равной 1.

Рисунок 4.10

Выполнение работы.

Движение тел с учетом сил сопротивления среды.

Вычислить скорость ( и ) и пройденный путь падающего тела ( и ) без учёта и с учётом сопротивления воздуха соответственно в моменты времени, указанные в таблице 4.2. Построить графики зависимостей , , , .

Сила сопротивления воздуха определяется по формуле , где коэффициенты А, В и С пропорциональны площади поперечного сечения тела, коэффициента обтекаемости, вязкости среды. Данные для расчета взять из таблицы 4.1.

Таблица 4.1

Таблица 4.2

Задание 1. Составить программу с использованием метода Эйлера для вычисления скорости и ускорения. Принять dt = 0.001. Заполнить таблицу 4.2

Задание 2. Построить графики зависимостей , , , .

Задание 3. Определить, за какой промежуток времени тело пролетит 50 м. Вычислить конечную скорость на этом участке, с учетом и без учета сопротивления воздуха. Определить, какую ошибку (в % ), можно сделать, если не учитывать сопротивление воздуха. Произвести те же вычисления для расстояний 100, 100 и 300 м. Результаты занести в таблицу 4.3. Сделать вывод (обосновать необходимость учитывать сопротивления воздуха).

Таблица 4.3

Задание 4. Построить зависимость скорости и координаты тела от времени с использованием метода Эйлера.

Задание 5. Решите эту же задачу с использованием встроенных функций пакета MathCAD.

Задание 6. Проследить влияние величины шага на точность результата. Для этого вычислить значения координаты различными методами. Результаты занести в таблицу 4.4.

Таблица 4.4

Задание 7. Провести исследование зависимости скорости равномерного падения тела в воздухе в зависимости от массы тела и коэффициентов сопротивления.

Задание 8. Решить задачу о движении пушечного ядра.