Лекция 7

Лекция № 11

Условный экстремум

Пусть на открытом множестве заданы функции , , , . Обозначим – множество точек, координаты которых удовлетворяют уравнениям:

, ,. (*)

Уравнения (*) называют ограничениями или уравнениями связи.

Определение. Точка называется точкой условного строгого максимума, если выполняется неравенство .

Если выполняется неравенство , то точку называют точкой условного строгого минимума.

Методы нахождения точек условного экстремума.

1. Метод исключения. Рассмотрим уравнения связи , . Если уравнения связи удается разрешить относительно каких-то переменных: 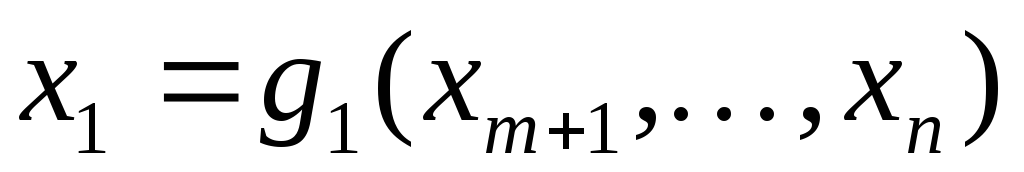, ,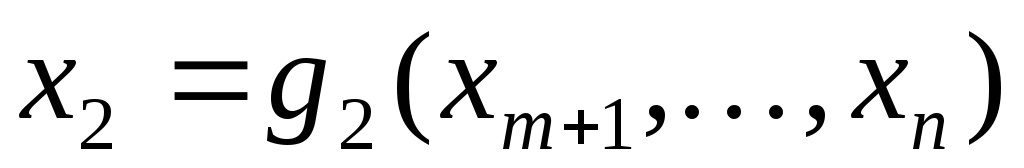,, 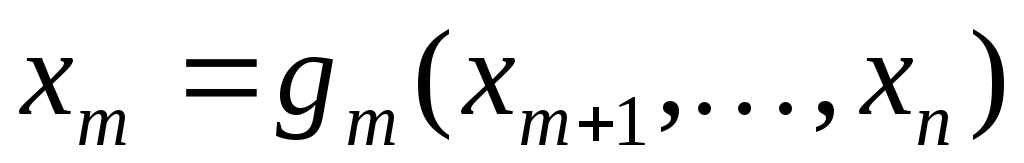то исследование функции на условный экстремум сводится к исследованию на обычный экстремум функции переменных.

Пример 1. Найти экстремум функции при условии, что и удовлетворяют уравнению связи .

Решение. Разрешим уравнение связи относительно переменной : . Подставив выражение для в функцию, получим . Исследуем на экстремум функцию одной переменной.

, .

Следовательно, точка минимума функции. Исходная функция в точке имеет условный минимум.

Пример 2. Найти условные экстремумы функции относительно уравнений связи , .

Решение. Разрешим уравнения связи относительно переменных и : , .

Подставив найденные значения и в выражения для , сведем задачу к исследованию на обычный (безусловный) экстремум функции . . Стационарные точки и .

, , . Следовательно, в точке функция имеет максимум , а в точке – минимум .

Исходная функция при заданных ограничениях имеет один условный максимум и один условный минимум .

2. Метод неопределенных множителей Лагранжа.

Пусть и непрерывно дифференцируемы в окрестности точки и ранг матрицы Якоби 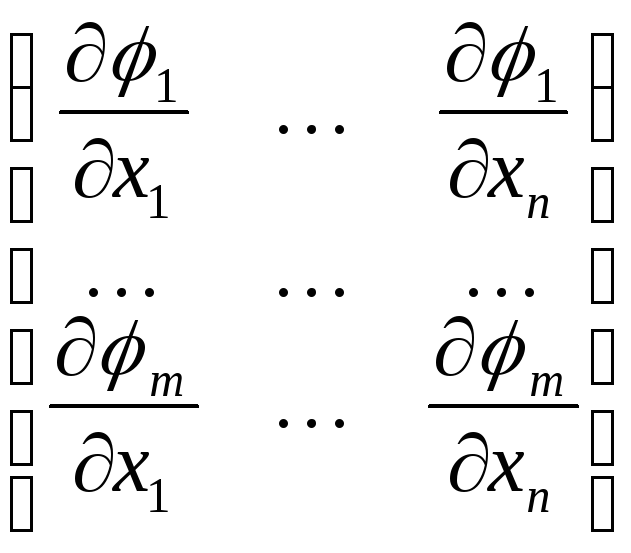в этой точке равен .

Функцию называют функцией Лагранжа. Коэффициенты – неопределенные множители Лагранжа.

Необходимые условия существования условного экстремума.

Для того, чтобы точка являлась точкой условного экстремума функции при связях необходимо, чтобы её координаты при некоторых значениях удовлетворяли системе уравнений

,

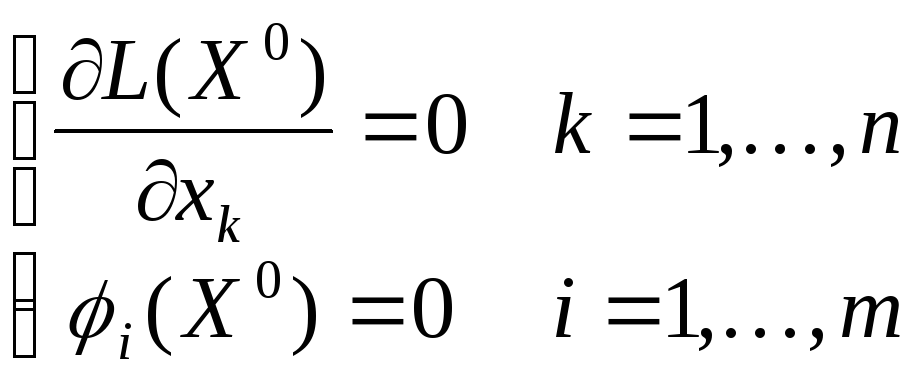т.е. – стационарная точка функции Лагранжа и её координаты удовлетворяют уравнениям связи.

Достаточные условия существования условного экстремума.

Пусть и дважды непрерывно дифференцируемы в окрестности точки , в которой выполняются необходимые условия существования условного экстремума функции при ограничениях .

Если при выполнении условий

, (1)

второй дифференциал является положительно (отрицательно) определенной квадратичной формой, то функция в точке имеет условный минимум (максимум).

Если при условиях (1) является неопределенной квадратичной формой, то в точке условного экстремума нет.

Пример 3. Найти экстремум функции при условии, что переменные и удовлетворяют уравнению .

Пример 4. Найти условный экстремум функции

относительно уравнения связи .

Решение. Функции и дважды непрерывно дифференцируемы. Матрица Якоби , .

Строим функцию Лагранжа .

Необходимые условия:

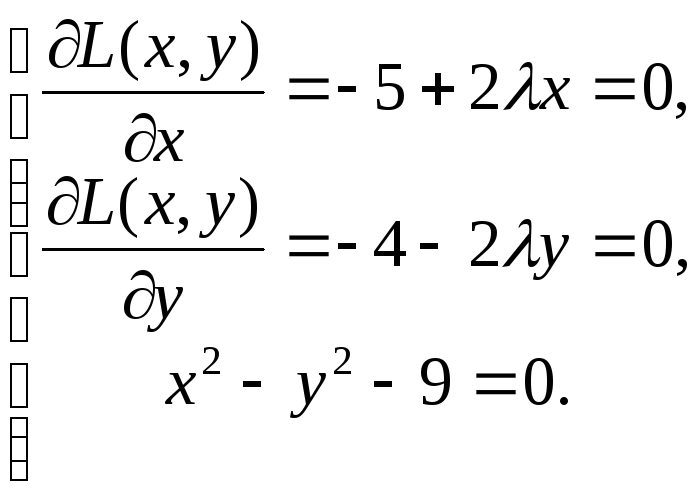
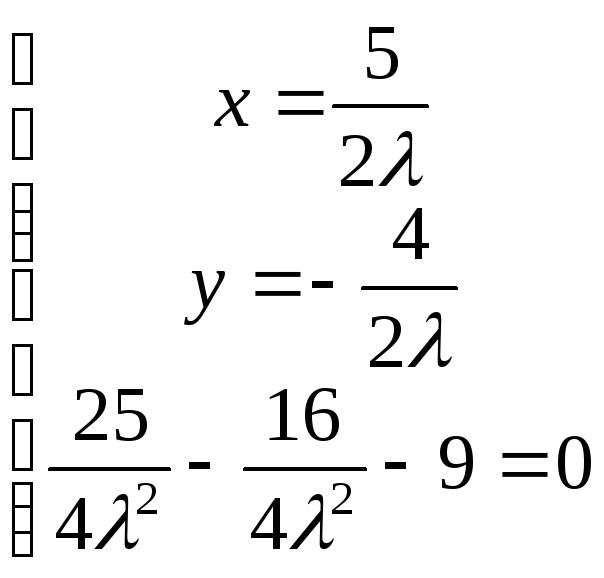
В точках и может быть условный экстремум.

Достаточные условия:

, , . , .

В точках и и связаны соотношением , поэтому и .

Точке соответствует поэтому и в точке условный максимум.

Точке соответствует поэтому и в точке условный минимум.

Наибольшее и наименьшее значение функции.

Hаибольшим значением функции в области называется число , если и для всех точек этой области выполняется неравенство .

Наименьшим значением функции в области называется число , если и для всех точек этой области выполняется неравенство .

Теорема Вейерштрасса. Для функции, непрерывной на ограниченном замкнутом множестве, существует на этом множестве точка, в которой функция принимает наибольшее значение и точка, в которой функция принимает наименьшее значение.

Функция, дифференцируемая в ограниченной области и непрерывная на её границе, достигает своего наибольшего и наименьшего значений либо в стационарных точках, либо в граничных точках области.

Пример 4. Определить наибольшее и наименьшее значения функции в области D: , , .

Решение. Указанная область есть треугольник (рис. 1). Стационарных точек функция не имеет, так как , .

Исследуем функцию на границах области. Граница состоит из трех отрезков [ОА], [АВ], [ОВ]. На отрезке , значит, для точек этого отрезка , .

Таким образом, задача свелась к нахождению наименьшего и наибольшего значений функции на отрезке . Так как , то функция принимает эти значения на концах отрезка, т. е. в точках и . Находим , .

Аналогично, для отрезка задача сводится к отысканию наибольшего и наименьшего значений функции на отрезке . Они реализуются на концах отрезка, т. е. в точках и , так как . Находим .

Отрезок определяется уравнением или при . Для этого отрезка имеем или и , т. е. наибольшее и наименьшее значения функция принимает на концах отрезка , в точках и . Сравнивая все полученные значения, заключаем, что

, .

Пример 5. Положительное число требуется разбить на три неотрицательных слагаемых так, чтобы их произведение было наибольшим.

Решение. Обозначим слагаемые , и . Ищем максимум функции . По смыслу задачи функция рассматривается внутри замкнутого треугольника , , .

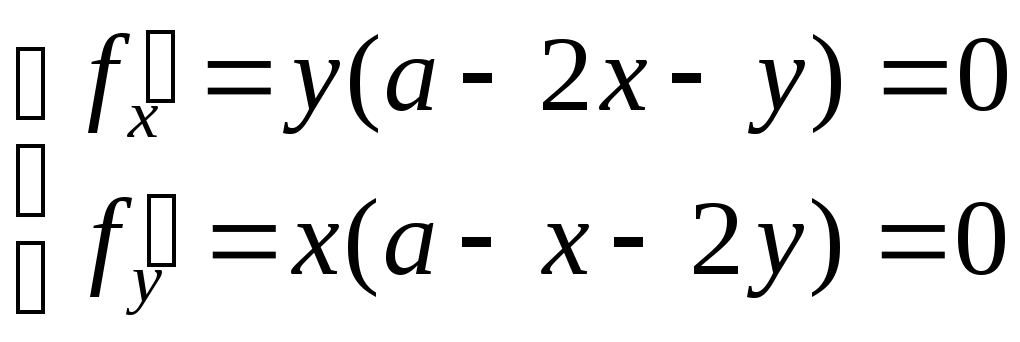. Внутренняя стационарная точка .

, , .

Матрица Гессе в стационарной точке 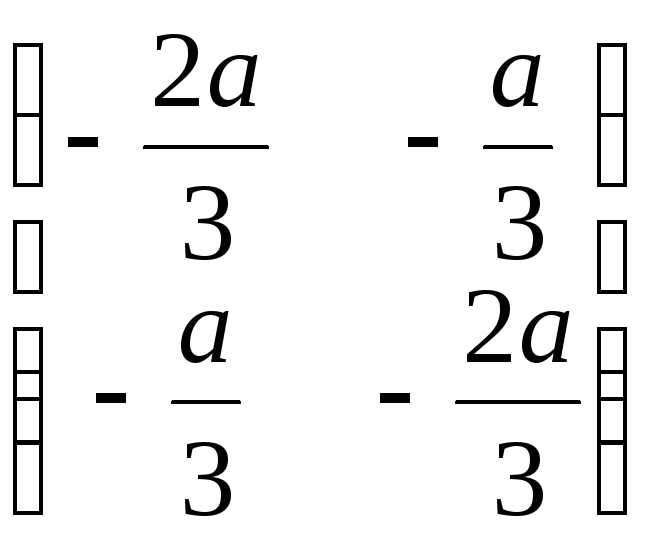. Так как , а , то в точке функция достигает максимума .

Поскольку на контуре треугольника , то этот максимум будет наибольшим значением.

Пример 6. (КИМ ЕГЭ 2006) Три числа, принадлежащих соответственно отрезкам , и , являются первыми членами арифметической прогрессии. Найдите, какие значения может принимать величина , где – первый член, а – разность прогрессии.

Р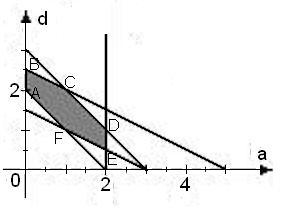ешение. Из условия задачи имеем: . Рассмотрим функцию , определенную на шестиугольнике . 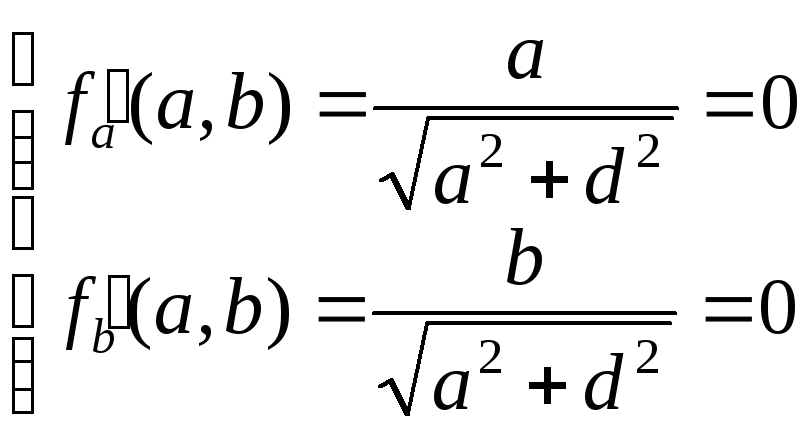, Стационарная точка не принадлежит шестиугольнику .

Найдем координаты вершин шестиугольника: , , , , , . Вычислим значения функции в вершинах: , , , , .

Значит, функция может принимать значения из отрезка .

5