Министерство образования и науки Российской Федерации

Красноярский государственный технический университет

ФИЗИКА

МЕХАНИКА

Лабораторный практикум

Утверждено Редакционно-издательским советом университета в качестве учебного пособия

Красноярск

2006

УДК 531/534 (07)

Рецензенты:

А.В. Шабанов, канд. физ.-мат. наук, научный сотрудник отдела молекулярной электроники КНЦ СО РАН; А.А. Черемисин, докт. физ.-мат. наук, проф., зав. кафедрой филиала ИГУПС

Физика. Механика: Лабораторный практикум для студентов всех специальностей и форм обучения. 2-е издание, исправленное и дополненное. Красноярск: ИПЦ КГТУ, 2006. 100 с.

Авторы

Е. М. Артемьев, А. Е. Бузмаков, Л. Л. Городилова, В. И. Злобин (отв. ред.), В. М. Зражевский, В. В. Кошманов, Л. И. Мамизерова,

Е. Е. Маторин, Н. М. Репина, В. Б. Шкуряева

Печатается по решению редакционно-издательского совета университета

© КГТУ, 2006

Печатается в авторской редакции

Гигиенический сертификат № 24.49.04.953.П.000338.05.01 от 25.05.2001 г.

Подп. в печать 21. 08. 2006. Формат 60x84/16. Бумага тип. № 1. Офсетная печать. Усл. печ. л. 5,8. Уч.-изд. л. 5,0. Тираж 500 экз. Заказ 492. С 155 Отпечатано в ИПЦ КГТУ 660074, Красноярск, ул. Киренского, 28

3

ОБЩИЕ СВЕДЕНИЯ

Выполнение лабораторных работ является обязательной составной частью при изучении дисциплины «Физика». Настоящий физический практикум по разделу «Механика» составлена в соответствии с программой для технических специальностей вузов. В физическом практикуме приведены 16 лабораторных работ, которые нужно выполнить студентам в первом (втором) семестре.

Цель практикума – научить применять физические законы, изученные в теоретическом курсе, к решению конкретных практических задач. Также при выполнении лабораторных работ студенты приобретают основные навыки исследовательской работы, учатся правильно пользоваться современными измерительными приборами и аппаратурой, знакомятся с методами измерений различных физических величин и обработкой полученных результатов, что является предпосылкой успешной дальнейшей работы в научной и заводской лаборатории.

Каждая работа содержит краткий теоретический материал, в котором излагается сущность изучаемого физического явления. Подробно раскрывается экспериментальная часть метода, положенного в основу изучения каждого опыта, а также приводится порядок выполнения работы и обработки результатов.

Практикум предназначен для студентов всех специальностей всех форм обучения.

ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ РАБОТ

На каждое лабораторное занятие студент должен приносить с собой: тонкую тетрадь, физический практикум, в котором дано описание выполняемой лабораторной работы, калькулятор, ручку, карандаш, линейку, миллиметровую бумагу для построения графиков.

Студент обязан являться в лабораторию подготовленным. К лабораторным занятиям студенты готовятся в часы их самостоятельной работы. Для этого необходимо тщательно изучить описание лабораторной работы по физическому практикуму и ознакомиться по учебнику с теоретическим материалом, необходимым для сознательного выполнения работы.

Обычно лабораторный курс тесно связан с лекционным курсом. В результате студент должен понимать физическую сущность явлений, которые будут изучаться в предстоящем эксперименте; отчетливо представлять те действия, которые необходимо произвести при работе с лабораторными установками.

Форма отчета выполняемой лабораторной работы должна быть подготовлена заранее дома.

4

ФОРМА ОТЧЕТА

Отчет каждой работы следует готовить в отдельной тонкой тетради (можно с двумя листами в зависимости от объема работы). Первый лист оформляется как титульный:

Министерство образования и науки Российской Федерации Красноярский государственный технический университет Кафедра “Физика”

Лабораторная работа № __ Полное название работы

Работу выполнил: студент _______

гр. №___

дата: ______.

Работу принял: преподаватель_______

Следующая страница должна содержать:

1)название работы;

2)цель работы;

3)описание приборов и принадлежностей с их характеристиками;

4)расчетные формулы с пояснением обозначений входящих в них величин;

5)таблицы наблюдений (с учетом числа измерений);

6)вычисление искомой величины;

7)вычисление относительной погрешности в % и абсолютной погреш-

ности;

8)окончательный результат с учетом абсолютной погрешности;

9)построенные графики;

10)выводы.

Студент не допускается к выполнению лабораторной работы, если: а) не оформлена предыдущая работа; б) имеется более одной несданной работы;

в) отсутствуют необходимые записи в отчете; г) студент не может удовлетворительно ответить на контрольные вопро-

сы преподавателя.

5

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

Погрешности измерений физических величин

Под измерением понимается сравнение измеряемой величины с другой величиной, принятой за единицу измерения. При измерении приходится выполнять три последовательные операции:

1)проверку и настройку приборов;

2)наблюдение их показаний и отсчет;

3)вычисление искомой величины из результатов измерений и оценку погрешности.

Измерения разделяют на прямые и косвенные. При прямых измерениях определяемая величина сравнивается с единицей измерения непосредственно или при помощи измерительного прибора, проградуированного в соответствующих единицах. К таким измерениям относятся измерения длины линейкой, штангенциркулем, микрометром; измерение массы тела, интервалов времени, величины напряжения или силы тока по шкале соответствующего прибора.

При косвенных измерениях интересующая нас физическая величина определяется вычислением по соответствующей формуле. Конкретная формула включает в себя ряд параметров, определяемых путем прямых измерений.

Например, при определении объёма V цилиндра необходимо измерить его диаметр D и высоту H, а затем по формуле V = πHD2 /4 вычислить объём.

Некоторые физические величины, входящие в расчетную формулу, остаются неизменными (параметры измерительной установки, физические и

математические константы), а некоторые величины xi при проведении серии опытов измеряются. Причем в общем случае в каждом из опытов значения

измеренной величины x1 , x2 , …, xn могут быть различными.

Это объясняется тем, что при измерении любой величины мы всегда получаем не истинное, а приближенное значение этой величины. Причина же связана как с измерительной точностью используемых инструментов и приборов, так и невозможностью учета всех внешних факторов, влияющих на конечный результат измерений.

Даже повторные измерения одной и той же величины при одних и тех же условиях и посредством одних и тех же приборов дают несколько различные результаты. Таким образом, любые измерения всегда выполняются с погрешностями или ошибками.

Погрешностью (или ошибкой) измерения называется отклонение данного результата измерения от истинного значения измеряемой физической величины.

6

Классификация погрешностей измерений

По характеру проявления погрешности подразделяют на систематические и случайные.

Систематическая погрешность – это составляющая ошибки измерения, которая при повторных измерениях остаётся постоянной или изменяется по определенному закону. Эти погрешности могут быть обусловлены неправильным выбором метода измерения, несовершенством или неисправностью приборов (например, измерения с помощью прибора, у которого смещен нуль).

Для того чтобы максимально исключить систематические погрешности, следует всегда тщательно анализировать метод измерений, сверять приборы с эталонами. В дальнейшем будем считать, что все систематические погрешности устранены, кроме тех, которые вызваны неточностью изготовления приборов и ошибкой отсчета. Эту погрешность будем называть аппаратурной.

Случайная погрешность – это составляющая ошибки измерения, которая изменяется случайным образом при повторных измерениях одной и той же величины. Причина данной погрешности заранее не может быть учтена. Случайные погрешности зависят от несовершенства наших органов чувств, от непрерывного действия изменяющихся внешних условий (изменение температуры, давления, влажности, вибрация воздуха и т. д.).

Хотя исключить случайные погрешности отдельных измерений невозможно, математическая теория случайных явлений дает возможность уменьшить влияние этих погрешностей на окончательный результат измерений и установить разумное значение погрешностей. Для этого необходимо выполнить не одно, а несколько измерений той же самой величины, причем, чем меньшее значение погрешности мы хотим получить, тем больше измерений нужно произвести.

Иногда при проведении измерений возникают грубые погрешности или промахи, являющиеся результатом небрежности отсчета по прибору или неожиданных сильных воздействий на измерения, неразборчивости записи показаний. Например, запись результата 26,5 вместо 2,65; отсчет по шкале 18 вместо 13 и т. д. При обнаружении грубой ошибки результат данного измерения следует сразу отбросить, а само измерение повторить.

Обработка результатов прямых измерений

Обычно в реальных измерениях присутствуют и случайные и систематические (аппаратурные) погрешности. Если вычисленная случайная погрешность прямых измерений равна нулю или меньше аппаратурной в два и большее число раз, то при вычислении погрешности косвенных измерений в

7

расчет должна приниматься аппаратурная погрешность. Если эти погрешности отличаются меньше, чем в два раза, то абсолютная погрешность вычисляется по формуле

x = xсл2

. + xсист2 . .

(1)

Случайная погрешность измерения обычно неизвестна, как неизвестно и истинное значение измеряемой величины. Поэтому задача элементарной обработки результатов измерений заключается в установлении интервала, внутри которого с заданной вероятностью находится истинное значение измеряемой физической величины.

Пусть в результате прямых измерений физической величины получен ряд ее значений: x1, x2, ..., xn.

Зная этот ряд чисел, нужно указать значение, наиболее близкое к истинному значению измеряемой величины, и найти величину случайной погрешности. Эту задачу решают на основе теории вероятностей, подробное изложение которой выходит за рамки нашего курса.

Наиболее вероятным значением измеряемой физической величины (близким к истинному) считают среднее арифметическое

	x + x +...+ x			1	n
< x >=	1 2	n	=		∑ x .		(2)
		n		n i=1		i

Здесь xi – результат i-го измерения, n – число измерений. В случае малого n правильная оценка погрешности основана на использовании распределения Стьюдента (t–распределения). Случайная ошибка измерения может быть оценена величиной случайной абсолютной погрешности xсл. , которую вычисляют по формуле

	x	=t(α,n)	1	n	(x −< x >)2		(3)
				∑		,
	сл.		n(n −1) i=1		i

где t(α, n) – коэффициент Стьюдента, зависящий от числа измерений n и доверительной вероятности α. Значение доверительной вероятности α задает сам экспериментатор.

Вероятностью случайного события называется отношение числа случаев, благоприятных для данного события, к общему числу равновозможных случаев. Вероятность достоверного события равна 1, а невозможного – 0.

Значение коэффициента Стьюдента, соответствующее заданной доверительной вероятности α и определенному числу измерений n, находят по табл. 1.

8

Из таблицы видно, что величина коэффициента Стьюдента и случайная погрешность измерения тем меньше, чем больше n и меньше α. Практически выбирают α = 0,95. Однако простое увеличение числа измерений не может свести общую погрешность к нулю, так как любой измерительный прибор дает погрешность.

					Таблица 1
Число	Доверительная вероятность α
измерений n	0,6	0,7	0,95		0,98
2	1,38	2,0	12,7		31,8
3	1,06	1,3	4,3		7,0
4	0,98	1,3	3,2		4,5
5	0,94	1,2	2,8		3,7
6	0,92	1,2	2,6		3,4
7	0,90	1,1	2,4		3,1
8	0,90	1,1	2,4		3,0
9	0,90	1,1	2,3		2,9
10	0,88	1,1	2,3		2,8
11	0,84	1,0	2,0		2,3
Поясним смысл терминов абсолютная погрешность				x и доверительная

вероятность α, используя числовую ось. Пусть среднее значение измеряемой величины <x> (рис. 1), а вычисленная абсолютная погрешность x. Отложим x от <x> справа и слева. Полученный числовой интервал от (<x> − x) до (<x> + x) называется доверительным интервалом. Внутри этого доверительного интервала находится истинное значение измеряемой величины x.

<x> − x <x> <x> + x	x
Рис. 1

Если измерения той же величины повторить теми же приборами в тех же условиях, то истинное значение измеряемой величины xист. попадет в этот же доверительный интервал, но попадание будет не достоверным, а с вероятностью α.

Вычислив величину абсолютной погрешности x по формуле (1), истинное значение x измеряемой физической величины можно записать в виде x = <x> ± x.

Величина абсолютной погрешности x результата измерений еще не определяет точности измерений. Для оценки точности измерения физической

9

величины подсчитывают относительную погрешность, которую обычно выражают в процентах:

	ε =	x	100 %.	(4)
		< x >

За меру точности измерения принимают величину 1/ε. Следовательно, чем меньше относительная погрешность ε, тем выше точность измерений.

Таким образом, при обработке результатов прямых измерений необходимо проделать следующее:

1.Провести измерения n раз (обычно 5).

2.Вычислить среднее арифметическое значение <x> по формуле (2).

3.Задать доверительную вероятность α (обычно берут α = 0,95).

4.По табл. 1 найти коэффициент Стьюдента, соответствующий заданной

доверительной вероятности α и числу измерений n.

5.Вычислить абсолютную погрешность по формуле (3) и сравнить ее с аппаратурной погрешностью. Для дальнейших вычислений взять ту из них, которая больше (см. пример на с. 11).

6.По формуле (4) вычислить относительную ошибку ε.

7.Записать окончательный результат

x = <x> ± x

с указанием относительной погрешности ε и доверительной вероятности α. Обычно кроме прямых измерений в лабораторной работе присутствуют

косвенные измерения.

Обработка результатов косвенных измерений

Пусть искомая физическая величина y связана с другими величинами x1, x2, ..., xn некоторой функциональной зависимостью

y = f(x1 , x2 , ..., xn).

(5)

Среди величин x1 , x2 , ..., xn имеются величины, полученные при прямых измерениях, и табличные данные. Требуется определить абсолютную ∆y и относительную ε погрешности величины y.

В большинстве случаев проще сначала вычислить относительную погрешность, а затем – абсолютную. Из теории вероятностей относительная погрешность косвенного измерения

ε = ε2x	+ε2x	+... +ε2x ..	(6)
1	2	n

							10
Здесьεx	=	1		∂f	xi , где	∂f	– частная производная функции по переменной
		y		∂xi
i						∂xi

xi, при вычислении которой все величины, кроме xi, считаются постоянными; ∆xi – абсолютная погрешность величины xi. Если xi получена в результате прямых измерений, то ее среднее значение <x> и абсолютную погрешность ∆x вычисляют по формулам (1) и (3). (Эти величины можно найти при помощи многофункционального калькулятора. Как это сделать, смотрите в прил. 1.) Для всех измеренных величин xi задается одинаковая доверительная вероятность α.

Если какие-либо из слагаемых в выражении (6) меньше на порядок (в 10 раз) других слагаемых, то ими можно пренебречь. Это нужно учитывать при

выборе табличных величин (π, g и др.), входящих в формулу относительной погрешности.

Конечный результат записывается в виде

y = <y> ± y.

Здесь <y> – среднее значение косвенного измерения, полученное по формуле

(5) при подстановке в нее средних величин xi, а ∆y – абсолютная погрешность косвенного измерения, найденная из определения относительной погрешности y = ε<y>. Обычно в абсолютной погрешности оставляют одну значащую цифру, а измеренную величину округляют до того разряда, в котором находится значащая цифра абсолютной погрешности.

Действия с приближенными числами

Многие считают, чем больше цифр содержит вычисленная или измеренная величина, тем она точнее. Вопрос о различной точности вычисления очень важен, так как завышение точности вычисления приводит к большому объему ненужной работы. Студенты часто вычисляют искомую величину с точностью до пяти и более значащих цифр. Следует понимать, что эта точность излишняя. Нет никакого смысла вести вычисления дальше того предела точности, который обеспечивается точностью определения непосредственно измерявшихся величин. Проведя обработку измерений, часто не подсчитывают ошибки отдельных результатов и судят об ошибке приближенного значения величины, указывая количество верных значащих цифр в этом числе.

Значащими цифрами приближенного числа называются все цифры, кроме нуля, а также нуль в двух случаях:

1) когда он стоит между значащими цифрами (например в числе 1071 – четыре значащих цифры);

11

2) когда он стоит в конце числа и когда известно, что единица соответствующего разряда в данном числе не имеется. Пример: в числе 5,20 три значащих цифры, и это означает, что при измерении мы учитывали не только единицы, но и десятые, и сотые, а в числе 5,2 – только две значащих цифры, и это значит, что мы учитывали только целые и десятые.

При вычислении промежуточных результатов сохраняют на одну цифру больше, чем рекомендуют правила (так называемая запасная цифра). Её обычно пишут меньшим размером. В окончательном результате запасная цифра отбрасывается. Если она окажется меньше пяти, ее следует просто отбросить, а если пять или больше пяти, то, отбросив ее, следует предыдущую цифру увеличить на единицу.

Обычно в абсолютной ошибке оставляют одну значащую цифру, а измеренную величину округляют до того разряда, в котором находится значащая цифра абсолютной ошибки.

Приближенные вычисления следует производить с соблюдением следующих правил:

1.При сложении и вычитании в результате сохраняют столько десятичных знаков, сколько их содержится в числе с наименьшим количеством десятичных знаков. Например: 0,8934 + 3,24 + 1,188 = 0,893 + + 3,24 + 1,188 =

=5,321 ≈ 5,32. Сумму следует округлить до сотых долей, т.е. принять равной

5,32.

2.При умножении и делении в результате сохраняют столько значащих цифр, сколько их имеет приближенное число с наименьшим количеством

значащих цифр. Например, необходимо перемножить 8,632×2,8×3,53. Вместо этого выражения следует вычислять 8,63×2,8×3,53 = 85,3 ≈ 85.

3. Результат расчета значений функций xn, n x , lg(x) некоторого приближенного числа x должен содержать столько значащих цифр, сколько их имеется в числе x. Например:

3,2 10−4 ≈ 1,8·10–2.

Рассмотрим пример. Пусть необходимо вычислить плотность вещества ρ, из которого изготовлен цилиндр. По определению

ρ = Vm ,

где m – масса тела, V – его объём. Объём цилиндра определяется формулой

V = πHD4 2 .

12

Здесь D – диаметр цилиндра, H – его высота.

Следовательно, расчётная формула для плотности вещества будет иметь вид

ρ =	4m		.	(7)
	πHD	2

Пусть D и H измерены штангенциркулем с ценой деления 0,1 мм, а масса определена на физических весах. В результате многократных измерений найдем средние значения <H> = 10,34 мм и <D> = 40,27 мм, а m = = 35,9 г. При подстановке этих данных в формулу (7) получим ρ = 2,726·103 кг/ м3. Если эту величину считать окончательным результатом, то запасная цифра 6 отбрасывается. Абсолютная погрешность измерения плотности в этом случае будет равна половине единицы последнего разряда, т. е. 5 кг/м3. Так обычно поступают при однократном измерении. В данном примере Н и D измерялись несколько раз, поэтому сначала надо вычислить относительную погрешность косвенного измерения плотности вещества по формуле

ε =

ρ

=

π 2

2

D 2

H 2

m 2

(8)

ρ

+

+

+

,

π

D

H

m

где D и H – абсолютные погрешности прямых измерений диаметра и высоты, а затем определить абсолютную погрешность плотности вещества из выражения ∆ρ = ερ. Пусть случайные абсолютные погрешности оказались

равными: Dсл. = 0,01 мм; Hсл. = 0,23 мм, а ∆m = 0,05 г. Сравним вычисленные случайные погрешности с аппаратурной, равной цене деления штанген-

циркуля. Dсл. < 0,1, поэтому в формулу (8) подставим D = 0,1 мм. А так как ( Hсл./ Hап.) < 3, то H вычисляем по формуле (3) и получаем 0,25 мм.

Значение π нужно выбрать таким, чтобы относительной погрешностью Δπ/π в формуле (8) можно было пренебречь. Из анализа измеренных величин и вычисленных абсолютных погрешностей D и H видно, что наибольший вклад в относительную погрешность измерения объема вносит ошибка измерения высоты. Вычисление относительной ошибки высоты дает εH =

= 0,0057. Если взять π = 3,1, то επ = 0,013, что превышает εH. Следовательно, значение π нужно взять 3,14. В этом случае Δπ/π ≈ 0,00064 (Δπ = 3,142 − − 3,14 = 0,002), что значительно меньше εH и относительную погрешность π можно не учитывать.

Вычисления относительной погрешности плотности по формуле (8) даёт значение ε = 0,00769, а ∆ρ = 0,0077·2,72· 103 = 20,9 кг/м3. Так как в абсолютной погрешности принято оставлять одну значащую цифру, то конечный результат следует записать в виде

13

ρ = (2,72 ± 0,02)103 кг/м3.

Необходимо сделать вывод по ответу. Полученное экспериментально значение величины плотности вещества, равное 2,72·103 кг/м3 с точностью до ошибки измерений, составляющей ±0,02·103 кг/м3, совпадает с табличным (теоретическим) значением плотности алюминия, равным 2,71·103 кг/м3.

Текст, выделенный курсивом, является шаблоном вывода по ответу в любой лабораторной работе.

Примечания:

1.Если измерения производят один раз или результаты многократных измерений одинаковы, то за абсолютную погрешность измерений нужно взять аппаратурную погрешность, которая для большинства используемых приборов равна цене деления прибора (более подробно об аппаратурной погрешности см. в пункте “Измерительные приборы”).

2.Если табличные или экспериментальные данные приводятся без указания погрешности, то абсолютную погрешность таких чисел принимают равной половине порядка (разряда) последней значащей цифры. Например,

если m = 2,47 г, тогда m = 0,5·0,01 = 0,005 г.
		Построение графиков
Результаты, полученные в ходе
выполнения лабораторной работы, часто
важно и	необходимо	представить
графической зависимостью. Для того
чтобы построить график, нужно на
основании	проделанных	измерений
составить таблицу, в которой каждому
значению одной из заданных величин
соответствует определенное значение
другой.
Графики необходимо выполнять на
миллиметровой бумаге. При построении			Рис. 2

графика значения независимой переменной следует откладывать на оси абсцисс (X), а значения функции – на оси ординат (Y). Около каждой оси нужно написать обозначение изображаемой величины и указать, в каких единицах она измеряется (рис. 2).

Для правильного построения графика важен выбор масштаба: кривая занимает весь лист, и размеры графика по длине и высоте получаются приблизительно одинаковыми. Масштаб должен быть простым. Проще всего, если единица измеренной величины (0,1; 10; и т. д.) соответствует 1, 2 или 5 см.

14

Следует иметь в виду, что пересечение координатных осей не обязательно должно совпадать с нулевыми значениями откладываемых величин. Каждое полученное экспериментальное значение отмечается на графике точкой, крестиком и т.д.

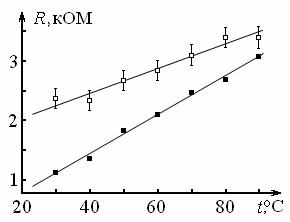
Погрешности указывают для измеряемых величин в виде отрезков длиной в доверительный интервал, в центре которых расположены экспериментальные точки. Так как указание погрешностей загромождает график, то делается это лишь тогда, когда информация о погрешностях действительно нужна: при построении кривой по экспериментальным точкам, при определении ошибок с помощью графика, при сравнении экспериментальных данных с теоретической кривой (рис. 2). Часто достаточно указать погрешность для одной или нескольких точек.

Через экспериментальные точки необходимо проводить плавную кривую. Нередко экспериментальные точки соединяют простой ломаной линией. Тем самым как бы указывается, что величины каким-то скачкообразным образом зависят друг от друга. А это является маловероятным. Кривая должна быть плавной, и может проходить не через отмеченные точки, а близко к ним так, чтобы эти точки находились по обе стороны кривой на одинаковом от нее расстоянии. Если какая-либо точка сильно выпадает из графика, то это измерение следует повторить. Поэтому желательно строить график непосредственно во время опыта. Тогда график может служить для контроля и улучшения наблюдений.

Вывод по графику (шаблон):

Полученный экспериментально график зависимости __________________

название функции словами

от _____________ имеет вид прямой (проходящей через начало координат,

название аргумента

параболы, гиперболы, плавной кривой) и качественно совпадает с теоретической зависимостью данных характеристик, имеющей вид ______________

формула

Измерительные приборы и учет их погрешностей

Для прямых измерений физических величин применяют измерительные приборы. Любые измерительные приборы не дают истинного значения измеряемой величины. Это связано, во-первых, с тем, что невозможно точно отсчитать по шкале прибора измеряемую величину; во-вторых, с неточностью изготовления измерительных приборов. Для учета первого фактора вводится погрешность отсчета x0, для второго – допускаемая погрешность

15

xд. Сумма этих погрешностей образует аппаратурную или абсолютную погрешность прибора xпр.:

x	=	x2	+	x2 .
ПР.		0		Д.

Допускаемую погрешность нормируют государственными стандартами и указывают в паспорте или описании прибора. Погрешность отсчета обычно берут равной половине цены деления прибора. Но для некоторых приборов (секундомер, барометр-анероид) – равной цене деления прибора (так как положение стрелки этих приборов изменяется скачками на одно деление) и даже нескольким делениям шкалы, если условия опыта не позволяют уверенно отсчитать до одного деления (например, при толстом указателе или плохом освещении).

Таким образом, истинную погрешность отсчета устанавливает сам экспериментатор, реально отражая условия конкретного опыта. Если допускаемая погрешность значительно меньше ошибки отсчета, то ее можно не учитывать. Обычно абсолютная погрешность прибора берется равной цене деления шкалы прибора.

Измерительные линейки обычно имеют миллиметровые деления. Для измерения рекомендуется применять стальные или чертежные линейки со скосом. Допускаемая погрешность таких линеек составляет 0,1 мм и ее можно не учитывать, так как она значительно меньше погрешности отсчета, равной ±0,5 мм. Допускаемая погрешность деревянных и пластмассовых линеек – ±1 мм.

Допускаемая погрешность измерения микрометра зависит от верхнего предела измерения и может составлять ±3–4 мкм (для микрометров с диапазоном измерения 0–25 мм). За погрешность отсчета принимают половину цены деления. Таким образом, абсолютную погрешность микрометра можно брать равной цене деления, т. е. 0,01 мм.

При взвешивании допускаемая погрешность технических весов зависит от нагрузки и составляет при нагрузке от 20 до 200 г – 50 мг, при нагрузке меньше 20 г – 25 мг.

Погрешность цифровых приборов определяется по классу точности.

16

ЛАБОРАТОРНАЯ РАБОТА № 1

МОДЕЛИРОВАНИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ И ИССЛЕДОВАНИЕ ЕЕ РАСПРЕДЕЛЕНИЯ

Цель работы: изучить статистические методы обработки опытных данных, подчиняющихся нормальному закону распределения случайных величин.

Оборудование: наручные часы с секундной стрелкой, электронный секундомер.

Краткие теоретические сведения

Случайной называется величина, изменяющаяся от опыта к опыту нерегулярно и, на первый взгляд, беспорядочно. Результат каждого отдельного измерения случайной величины практически непредсказуем. Однако совокупности результатов измерений подчиняются статистическим закономерностям, изучение которых служит одной из основ теории и практики физического и инженерного эксперимента. Существует множество законов распределения случайных величин. Одним из наиболее распространенных законов является нормальный закон распределения, описываемый функцией Гаусса:

	ρ(t) =		1	exp[−	(t −<t>)2	],	(1)
		σ	2π		2σ2

где ρ(t) – плотность нормального распределения случайной величины t, σ – среднеквадратичная ошибка или стандарт.

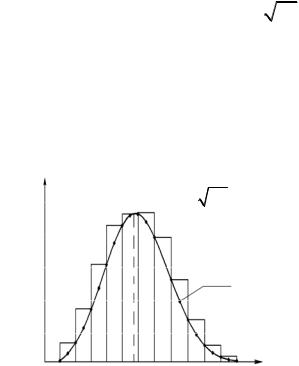
Закономерность распределения значений изучаемой случайной величи-

ны t становится наглядной,

если построить

гистограмму

–

ступенчатую

диаграмму, показывающую, как часто при

N

измерениях появляются значения, попа-

ρmax =

1

дающие в

тот

или иной

из

равных

N t

σ 2π

интервалов

t,

расположенных

между

наименьшим и наибольшим из всех

наблюдаемых значений величины t.

ρ(t)

Гистограмму

строят

в

следующих

координатах (рис. 1): ось абсцисс – изме-

ряемая величина t; ось ординат –

N/N t.

Здесь N – полное число измерений; N –

число результатов, попадавших в интервал

tmin

<t>

tmax

t

[t, t + t].

N/N определяет долю всех

Рис. 1

Частное

17

результатов, попавших в указанный интервал, и характеризует собой вероятность попадания в него результата отдельного измерения. Отношение этой величины к ширине заданного интервала N/N t называется «плотностью вероятности».

При очень большом числе измерений ( N →∞) вместо ступенчатой гистограммы получается плавная кривая зависимости

						1 dN
ρ(t)=			N		=			.	(2)
	lim
						N dt
	N→∞		N t
	t→0

Эту функцию называют плотностью вероятности или законом распределения по t. Чтобы сравнить наблюдаемое распределение с нормальным распределением (1), нужно найти по данным измерений параметры <t> и σ функции Гаусса (приближенно, поскольку число измерений ограничено). Параметр <t> есть среднее арифметическое случайной величины

<t >= 1 (t +t +...+t				)= 1 ∑ti .			(3)
						N
		1 2	n			i=1
	N				N

Параметр σ является средним квадратичным отклонением наблюдений от среднего <t>:

σ=	1	N t −<t > 2 .		(4)
	N −1i∑=1( i		)

Из анализа формулы (1) следует, что плотность нормального распределения имеет максимум

	ρ	(t)=	1	(5)
			σ 2π
	max

при значении t = <t> и симметрична относительно <t>. Нетрудно сравнить «наибольшую высоту гистограммы» и максимальное значение функции Гаусса (5).

Для количественной проверки того, насколько хорошо полученные результаты соответствуют нормальному распределению, можно воспользоваться соотношением (6), в котором вероятность Р12 попадания результата измерения в интервал (t1, t2), c одной стороны, может быть вычислена как интеграл функции Гаусса в этих пределах, а с другой – найдена как относительное число наблюдений N12 , результаты которых попали в этот интервал:

	18
	t
			1
		∫ ρ(t)dt ,
				(6)
P
	= t		2
12
	N / N
			12

При сравнении наблюдаемого распределения с нормальным (1) можно воспользоваться известными значениями вероятности распределения случайной величины для наиболее употребительных в технике измерений пределов:

t(<t> − σ; <t> + σ),	Pσ = 0,68;
t(<t> − 2σ; <t> + 2σ),	P2	σ = 0,95;
t(<t> − 3σ; <t> + 3σ),	P3	σ = 0,997.

Измерения и обработка результатов

В данной работе моделирование случайной величины осуществляется следующим образом. При помощи обычных часов с секундной стрелкой задают некоторый промежуток времени t и измеряют его высокочувствительным цифровым частотомером или электрическим секундомером, вручную нажимая кнопки «старт» и «стоп».

Выполнять работу рекомендуется двум студентам. Первый многократно задает определенные промежутки времени по часам, подавая команду «старт» и «стоп». Второй нажимает кнопки и записывает отсчеты по прибору. В этом случае результаты измерений будут независимыми, что должно привести к нормальному (Гауссовому) распределению случайной величины.

1.Проведите 30–50 раз измерение выбранного промежутка времени. Можно задать промежуток времени от 5 до 10 секунд. Показания цифрового частотомера занесите во второй столбец табл. 1.

2.Найдите в табл. 1 наименьший tmin и наибольший tmax из результатов

наблюдений. Промежуток (tmin – tmax) разбейте на 6–10 равных интервалов t. Границы интервалов занесите в табл. 2.

3.Подсчитайте число результатов наблюдений в табл. 2, попавших в каждый интервал ti, и заполните второй столбец табл. 2.

4.Вычислите экспериментальные значения плотности вероятности

попадания случайной величины в каждый из интервалов ti. Заполните третий столбец табл. 2.

5. Постройте гистограмму (рис. 1), для чего по оси абсцисс откладывайте интервалы ti, являющиеся основаниями прямоугольников, высота которых равна плотности вероятности ρi.

					19
											Таблица 1
Номер		ti , c		(ti − <t>)2 , c2
опыта											σ = ... , c
1
2
...
30										ρm a x = ... , c−1
		<t>, с		Σ(ti − <t>)2 , с2
											Таблица 2
Границы				N			N	, с−1			ρ, с−1
						N	t
интервалов, с

6.Вычислите <t> по (3) и σ по (4). Можно воспользоваться результатами двадцати наблюдений. Полученные значения занесите в табл. 1.

7.По формуле (5) найдите максимальное значение плотности вероятно-

сти ρmax при t = <t>. Результаты занести в табл. 1. Сравнить полученные значения ρmax с наибольшей высотой гистограммы.

8. Для значений t, соответствующих границам выбранных интервалов, вычислите по функции Гаусса (1) значения плотности вероятности ρ(t) и занесите их в четвертый столбец табл. 2.

9. Нанесите все расчетные точки на график, на котором изображена гистограмма, и проведите через них плавную кривую. Сравните их. В чем причина неполного соответствия кривой Гаусса и гистограммы?

						Таблица 3
	Границы	Интервал, с		N1 2	N1 2 /N	P1 2
	интервалов	от	до
	<t> ± σ
	<t> ± 2σ
	<t> ± 3σ

10. Проверьте, насколько точно выполняется в опытах соотношение (1). Вычислите границы интервалов, указанных в первом столбце табл. 3. По

20

данным табл. 1 подсчитайте число наблюдений N12, попадающих в каждый из трех интервалов, а также отношение N12/N (6). Сравните их с известными значениями Р12, соответствующими нормальному распределению случайных величин (1). В чем причина небольшого расхождения?

Контрольное задание

При обработке результатов измерения емкости для партии конденсаторов получено <C> = 1,1 мкФ, σ = 0,1 мкФ. Если взять коробку со 100 конденсаторами из этой партии, то сколько среди них можно ожидать конденсаторов с ёмкостью меньше 1 мкФ? Больше 1,3 мкФ? Меньше 0,8 мкФ?

Контрольные вопросы

1.Какие измерения называются прямыми? Косвенными?

2.Что называется абсолютной, относительной, систематической и случайной погрешностями измерений?

3.Что такое средняя квадратичная погрешность, доверительный интервал и доверительная вероятность?

4.Что такое дисперсия измерений?

5.Как распределяются случайные погрешности измерений? Как влияет дисперсия измерений на это распределение?

5.Какими свойствами обладает нормальное распределение результатов измерений?

6.Каков порядок обработки результатов измерений?

7.Как найти случайную погрешность среднего значения из результатов эксперимента?

8.Каков смысл введения коэффициента Стьюдента? Как его опреде-

лить?

9.Как найти погрешность косвенных измерений?

21

ЛАБОРАТОРНАЯ РАБОТА № 2

ПРОВЕРКА ВТОРОГО ЗАКОНА НЬЮТОНА НА МАШИНЕ АТВУДА

Цель работы: проверить второй закона Ньютона.

Оборудование: машина Атвуда с грузами и перегрузками, электрический секундомер.

Краткие теоретические сведения

По второму закону Ньютона произведение массы частицы на ускорение равно действующей силе:

ma = F .

(1)

В общем случае результирующая силаG является векторной суммой всех действующих на частицу сил: F =∑Fi . Выражение (1) называют также

основным законом динамики поступательного движения. Оно справедливо не только для частицы, но и для тела, движущегося поступательно.

Если на телоG постояннойG массы m действовать последовательно различными силами F1 и F2 , тогда по второму закону Ньютона тело будет двигаться

также с различными по величине ускорениями a1 и a2 , отношение которых равно отношению сил:

a1		=	F1	при m = const.	(2)
			F
a	2
			2

С другой стороны, из уравнения (1) следует, что если на тела с различ-

ными массами m1 и m2 действуют равные силы F , то тела будут двигаться с разными по величине ускорениями a1 и a2 , отношение которых обратно

отношению масс:

	a1	=	m2	при F = const.	(3)
	a2		m1

Описание установки и метода измерений

Соотношения (2) и (3) являются следствиями второго закона Ньютона и их можно проверить на машине Атвуда.

22

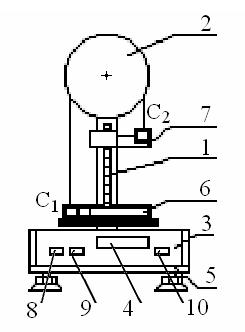
Принцип устройства машины Атвуда показан на рис. 1. На вертикальной стойке 1 с сантиметровыми делениями расположен легкий блок 2. Через блок перекинута нить с подвешенными на её концах грузами C1 и C2 равной массы m. Груз С1 удерживается в нижнем положении электромагнитом. На грузы помещаются перегрузки с разными массами (на рис. 1 не показаны). Время движения грузов измеряется электронным секундомером 3 с цифровой индикацией 4, который находится на основании 5 прибора. К электронному секундомеру подключены фотоэлектрические датчики 6 и 7. Датчик 7 включает секундомер, а датчик 6 – выключает. На лицевой панели прибора рас-

Рис. 1 положены также три клавиши: 10 (сеть) – выключатель сети; 8 (пуск) – отключение электромагнита и запуск секундомера; 9 (сброс) – включение электромагнита

и подготовка секундомера к следующему измерению.

ЗАДАНИЕ № 1

Цель работы: на машине Атвуда проверить следствие (2) второго закона Ньютона при постоянной движущейся массе. По результатам измерений необходимо определить отношение сил и отношение ускорений. Полученные результаты сравнить. Следствие (2) проверяется при движении системы тел под действием силы тяжести.

При движении системы грузов в подшипниках блока действует сила трения. Её можно компенсировать силой тяжести грузика, добавляемого к грузу C2, движущемуся вниз. Если после компенсации силы трения на левый и правый грузы положить перегрузки массой m1 слева и m2 справа (m2 > m1), то они выведут систему из равновесия, и она будет двигаться равноускоренно.

Тогда результирующая сила F1, сообщающая системе тел ускорение a1, равна разности сил тяжести, действующих на перегрузки:

F1 = m2 g − m1 g = (m2 − m1 )g.

(4)

Если переложить перегрузок m1 с левого груза на правый, то ускорение системы тел a2 возрастет, и соответствующая результирующая сила будет равна

F2 = m2 g + m1 g = (m2 + m1 )g.

(5)

			23
	Отношение сил X1 есть	F1		m2	−m1
	X1 =		=			.	(6)
		F2		m2
					+ m1

По условиям опыта под действием разных сил F1 и F2 система тел проходит равноускоренно одинаковый путь h, поэтому

h =		a1t12					a2 t22
				=					.	(7)
		2					2
Отношение ускорений X2 есть
X			a					t2		(8)
			1			2			.
	2 =					=
			a					t2
			2			1

Порядок выполнения работы

1.Ознакомиться с машиной Атвуда.

2.Скомпенсировать силу трения в блоке, добавляя к правому грузу, движущемуся вниз, небольшой грузик (кусочек пластилина или проволоки). При компенсации силы трения система тел, выведенная из равновесия легким толчком, движется равномерно. Равномерность движения определяется визуально. (Во время дальнейшей работы нужно следить за тем, чтобы положение грузов «левое» и «правое» не менялось.)

3. Положить на левый и правый грузы перегрузки известной массы m1

иm2, где правый перегрузок m2 > m1.

4.Измерить время t1 движения системы. Опыт повторить пять раз.

5.Оба перегрузка m1 и m2 положить на правый груз. Измерить время движения t2 также пять раз.

Результаты всех измерений записать в табл. 1.

						Таблица 1
					Масса перегрузка
Номер	Время	2	Время	2
опыта	t1i, с	(t1i − <t1>)	t2i, c	(t2i − <t2>)
					m1, г	m2, г
1
2
3
4
5
t(α, n)	<t1>, c	∑(t1i − <t1>)2	<t2>, c	∑(t2i − <t2>)2	m1, г	m2, г

24

6. По формуле (6) вычислить отношение сил, обозначенное через X1, по формуле (8) – отношения ускорений X2, подставляя средние значения времени

<t1> и <t2>.

7. Вычислить абсолютную погрешность измерения времени t1:

	t1 = t(α, n)	1	∑(t1i − < t1 >)2 .
		n(n −1)
	Здесь t(α, n) – коэффициент	Стьюдента для доверительной вероятности

α = 0,95 и числа измерений n = 5. Аналогично вычисляется абсолютная

	погрешность измерения времени		t2.
	8. Вычислить относительную погрешность измерения отношения уско-
	рений
			t1	2		t2	2
	ε = 2				+		.
			< t1 >			< t2 >

9. Вычислить абсолютную погрешность измерения отношения ускоре-

ний:

X2 = εX2 .

10. Вычислить абсолютную погрешность измерения отношения сил:

X	1	=		2		m		m2	+ m2 .
			(m		+ m		) 2	1	2
		1				2

Здесь m – абсолютная погрешность измерения массы перегрузков. 11. Записать результаты вычислений в виде

X1 = …± … , X2 = …± … .

12. Сравнить полученные значения X1 и X2, которые должны совпадать в пределах ошибок:

X1 − < X >2 ≤ ( X1 )2 + ( X2 )2 .

Выполнение этого неравенства является критерием выполнимости следствия (2) второго закона Ньютона. Сделать вывод.

25

ЗАДАНИЕ № 2

Цель работы: на машине Атвуда проверить следствие (3) второго закона Ньютона при постоянной силе. По результатам измерений определить отношение масс и отношение ускорений. Полученные результаты сравнить. Следствие (3) проверяется при движении системы тел под действием силы тяжести.

Если на правый груз C2, движущийся вниз, поместить перегрузок массой m0, то на систему тел будет действовать сила, равная силе тяжести m0g перегрузка. Движение будет равноускоренным с ускорением а1.

Общая масса системы

m1 = 2M +m0 ,

(9)

где M – масса груза.

Если на левый и правый грузы добавить перегрузки одинаковой массы m3, то результирующая сила не изменится. Однако система будет двигаться с другим ускорением а2, поскольку изменилась движущая масса. Общая масса системы тел увеличилась на 2m3 и стала равной

m2 = 2M + m0 +2m3 .

(10)

Найдем отношение масс:

Y1	=	m2	=	2M +m0 +2m3	.	(11)
		m1
				2M +m0

В обоих случаях система тел проходит равноускоренно одинаковый путь, следовательно

	a1t12	=	a2 t22		(12)
	2		2 .

Из равенства (12) найдем отношение ускорений:

Y2 =	a	1		t 2
			=	2	.	(13)
	a2
				t12

Порядок выполнения работы

1.Ознакомиться с машиной Атвуда.

2.Скомпенсировать силу трения в блоке (согласно п. 1 задания 1).

26

3.На правый груз поместить перегрузок известной массы m0.

4.Измерить время t1 движения системы тел. Опыт повторить пять раз. Результаты измерений записать в табл. 2.

Таблица 2

Номер	Время	(t1 i − <t1 >)2	Время	(t2 i − <t2 >)2	Масса	Масса перегр.
опыта	t1 i , c		t2 i , c		груза M, г
						m0 , г	m3 , г
1
2
3
4
5
t(α,n)	<t1 >, c	∑(t1 i −<t1 >)2	<t2 >, c	∑(t2 i−<t2 >)2	M, г	m0 , г	m3 , г

5.Изменить общую массу системы тел, добавляя к левому и правому

грузам перегрузки одинаковой массы m3. Измерить время t2 движения системы также пять раз. Результаты всех измерения записать в табл. 2.

6.По формуле (11) вычислить отношение масс. По формуле (13) вычислить отношение ускорений, подставляя средние значения времени <t1> и

<t2>.

6. Вычислить случайную абсолютную ошибку измерения времени t1:

t = t(α, n) ∑(t1i − < t1 >)2 .
1	n(n −1)

Здесь t(α,n) – коэффициент Стьюдента для доверительной вероятности α = 0,95 и числа измерений n = 5.

Аналогично вычислить абсолютную ошибку измерения времени t2.

7. Вычислить относительную ошибку измерения отношения ускорений

			t1	2		t2	2
	ε = 2				+		.
			< t1 >			< t2 >

8. Вычислить абсолютную ошибку измерения отношения ускорений:

Y2 = εY2.

9. Вычислить абсолютную ошибку измерения отношения масс:

		2	m		m	3	2
Y1	=							+1.
		2M	+ m0	5	2M +m0