
шпора матан
.docx|
1Понятие множества и подмножества. Пустое множество. Операции над множествами. Взаимно однозначное соответствие. Эквивалентные множества, счетные и несчетные множества Мн-ва – первичное понятие, на уровне здравого смысла, его не возможно точно определить. Для описания мн-в единая символика, а именно, если в мн-во А входят только эл. х, которые обладают некоторым св-вом S(x), то тогда мн-во А описывается А={х вып-ся усл S(x)}. Подмн-ва – если А и В 2 мн-ва и все эл-ты мн-ва А сод-ся в В, то А наз-ся подмн-вом В, А В, если в В сод-ся эл-ты отличные от эл-тов мн-ва А, то В строго шире А, то А наз-ся собственным подмн-вом В. А⊂В. А=В- мн-ва совпадают. Операции с мн-воми А В={х!х принадл. либо А, либо В} – обьединение мн-в А и В. А∩ В={хх∈А и х∈В} пересечение мн-в А и В. А\ В={хх∈А, но х∉В}дополн. к м-ву В во мн-ве А Числовые мн-ва R,N,Z,Q - стандартные обозначения мн-в на числ. прямой. (а,в)= {ха<х<в} – интервал из R (открытый промежуток, т.к. не содержит границ) [а,в] – замкнутый промежуток сод. гранич. т-ки. (а,в] – полуинтервал. Окрестностью т-ки х наз-ся любой интервал содержащий т-ку х, необязательно симметричную. Для того, чтобы сравнить два каких-либо множества А и В, между их элементами устанавливают соответствие. Если это соответствие взаимооднозначное, то множества называются эквивалентными или равномощными, А В или В А. Пусто́е мно́жество— множество, не содержащее ни одного элемента. Взаимно однозначным соответствием между множествами X и Y называется соответствие (соответственно, отображение), обладающее следующими тремя свойствами: 1) каждому элементу множества X соответствует один и только один элемент множества Y; 2) двум различным элементам множества X всегда соответствуют два различных элемента множества Y; 3) всякий элемент множества Y соответствует хотя бы одному элементу множества X. Множество, равномощное множеству натуральных чисел, называется счетным. Множество, не являющееся конечным или счетным, называется несчетным Множества и называются эквивалентными или равномощными, если между ними можно установить взаимно однозначное соответствие.
5. Связь между бесконечно малыми и бесконечно большими величинами. Основные теоремы о пределах. Предельный переход в неравенствах Cвязь.
Eсли
f
(x)
— бесконечно большая функция, то
В
самом деле, пусть
( Так
как |f
(x)|
> K
, то
Будем
считать, что
( Это
означает, что
Теорема 1. (о единственности предела функции). Функция не может иметь более одного предела.
Теорема
2. Если
функции f(x) и g(x) имеют пределы в
точке
1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.
3)предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.
а
функция f(u) непрерывна в точке
Переход. Теорема. Если элементы сходящейся последовательности {xn}, начиная с некоторого номера, удовлетворяют неравенству xn ≥ b (xn ≤ b), то и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b).
9. Точки разрыва, их классификация. Графические иллюстрации. Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х0, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х0 является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной. Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом. Если
односторонний предел (см. выше)
Если
односторонний предел (см. выше)
Определение. Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.
Определение. Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.
Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х0, достаточно того, что она определена слева и справа от нее. Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом поговорим ниже.
Определение. Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
12. Понятие дифференциала. Свойства дифференциала. Производные и дифференциалы высших порядков функции одной переменной и их свойства Дифференциалом функции y = f(x) называется главная линейная относительно D x часть приращения D y, равная произведению производной на приращение независимой переменной dy = f'(x)D x. Cвойства: d c = 0; d(c u(x)) = c d u(x); d(u(x) ± v(x)) = d u(x) ± d v(x); d(u(x) v(x)) = v(x) d u(x) + u(x)d v(x); d(u(x) / v(x)) = (v(x) d u(x) - u(x) d v(x)) / v2(x) еще одно свойство, которым обладает дифференциал, но не обладает производная. Рассмотрим функцию y = f(u), где u = f (x), то есть рассмотрим сложную функцию y = f(f(x)). Если каждая из функций f и f являются дифференцируемыми, то производная сложной функции согласно теореме ( 3) равна y' = f'(u)· u'. Тогда дифференциал функции dy = f'(x)dx = f'(u)u'dx = f'(u)du, так как u'dx = du. То есть dy = f'(u)du. Последнее равенство означает, что формула дифференциала не изменяется, если вместо функции от x рассматривать функцию от переменной u. Это свойство дифференциала получило название инвариантности формы первого дифференциала. Рассмотрим
функцию
Дифференциал выс. порядков dy= f‘(x)dx – диф. первого порядка ф-ции f(x) и обозначается d^2y, т.е. d^2y=f‘‘(x)(dx)^2. Диф. d(d^(n-1)y) от диф. d^(n-1)y наз-ся диф. n-ного порядка ф-ции f(x) и обознач. d^ny. Теорема Ферма. Пусть ф-ция f(x) определена на интервале (a,b) и в некоторой т-ке х0 этого интервала имеет наибольшее или наименьшее знач. Тогда если в т-ке х0 пр-ная, то она = 0, f‘(x0)=0. 2)Теорема Ролля. Пусть на отрезке [a,b] определена ф-ция f(x) причем: f(x) непрерывна на [a,b]; f(x) диф. на (a,b); f(a)=f(b). Тогда т-ка с(a,b), в которой f‘(c)=0. 3)Теорема Логранджа. Пусть на отрезке [a,b] определена f(x), причем: f(x) непр. на [a,b]; f(x) диф. на [a,b]. Тогда т-ка c(a,b) такая, что справедлива ф-ла (f(b)-f(a))/b-a= f‘(c). 4)Теорема Коши. Пусть ф-ции f(x) и g(x) непр. на [a,b] и диф. на (a,b). Пусть кроме того, g`(x)0. Тогда т-ка с(a,b) такая, что справедл. ф-ла (f(b)-f(a))/(g(b)-g(a))=f‘(c)/g‘(c).
|
2Понятие отображения (функции), его области определения и области значения. Основные элементарные функции. Обратное отображение. Отображе́ние или фу́нкция— одно из основных понятий математики, выражающее зависимость одной величины от другой. Множество X тогда называется о́бластью определе́ния отображения F (обозначается D(f) или D(x).). Множество Y — о́бластью значе́ний отображения F.(обозначается E(f) или E(y). Область определения функции - все значения, которые принимает независимая переменная. Область значений функции (множество значений)- все значения, которые принимает функция. Основные простейшие элементарные функции: Линейная функция y=kx+b; Степенная функция y=x?; Квадратичная функция; Показательная функция (0 <a1); Логарифмическая функция x (0 < a1); Тригонометрические функции: sin x, cos x, tg x, ctg x; Обратные тригонометрические функции: arcsin x, arccos x, arctg x, arcctg x. Таким образом, определено отображение , которое называется обратным отображению f, или обратной функцией функции f.
6.Односторонние пределы. Односторонний предел по Коши Число
Число
Свойства
Основные свойства односторонних пределов идентичны свойствам обычных пределов и являются частными случаями свойств пределов вдоль фильтра. Для существования (двустороннего) предела функции необходимо и достаточно, чтобы оба односторонних предела существовали и равнялись между собой
10. Понятие производной функции одной переменной. Геометрическая и экономическая интерпретации производной. Определение пр-ной 1) Пусть ф-ция y=f(x) определена по крайней мере в окр-тях т-ки х0, таким приращения х эл-нт. Составим соотв. ему приращения ф-ции т-ки х0. y=f(x0)=f(x0+x)-f(x0) Образуем разностное отношение y/x=f(x0)/x (1) (это разностное отношение явл. ф-цией х, т.к. х0-фиксирована, причем при х0 мы имеем дело с неопр. 0/0). Опр. Пр-ной ф-ции y=f(x) наз-ся предел разностного отношения 1 (при условии если он ), когда х0. Производная это предел отношения приращения в данной т-ке к приращению аргумента при усл., что посл-ть к 0. Эта производная обозначается через df(x0)/dx или f‘(x0), у‘ (если данная т-ка х0 подразумевается или же речь идет о пр-ной в любой текущей т-ке х. Итак согласно определению f‘(x0)=lim(x0) (f(x0+x)-f(x0))/x (2) Если ф-ция f(x) имеет в т-ке х0 пр-ную, т.е. предел в правой части (2) , то говорят что f(x) дифференц. в т-ке х0. Геометрический смысл производной. Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
рассмотрим график функции y = f ( x ):
видно,
что для любых двух точек A
и B
графика функции:
13.Возрастание и убывание функции. Достаточное условие строго возрастания (убывания) функции на интервале. Экстремум функции
Возрастание
и убывание дифференцируемой функции
связано со знаком её производной.
Напомним, что функция
Теорема. Для того чтобы функция f (x), дифференцируемая в точке х0 Î (а, b), возрастала (убывала) в точке х0 , достаточно, чтобы f ' (x0) > 0 (f ' (x0) < 0). Теорема. Для того чтобы функция f (x), дифференцируемая в точке х0 Î (а, b), возрастала (убывала) в точке x0, необходимо, чтобы её производная в точке х0 была неотрицательной f ' (x0) ≥ 0 (неположительной f ' (x0) ≤ 0). Теорема. Если функция f (x) определена на отрезке [а, b], дифференцируема в точках х Î (а, b) иf ' (x) > 0, ( f ' (x) < 0),то функция f (x) возрастает (убывает) на отрезке [а, b ]. Экстремум—максимальноеили минимальное значение функции на заданном множестве Пусть
дана функция 1.x0 называется точкой локального максимума функции
|
3.Числовая последовательность. Предел числовой последовательности. Предел функции в бесконечности и в точке. Бесконечно малые величины. Пусть множество X — это либо множество вещественных чисел , либо множество комплексных чисел . Тогда последовательность элементов множества X называется числовой последовательностью. Число
Число А называется пределом функции y=f(x) при х стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа E>0, найдется такое положительное число S>0 (зависящее от E)^ что для всех х таких что |x|>S, верно равенство |f(x)-A|<E Число А называется пределом функции y= f(x) при х стремящемся к х0 если для любого, даже сколько угодно малого положительного числа E>0 найдется такое положительное число S>0 (зависящее от E), что для всех х, не равных х0 и удоволетсворяющих условию |x-x0|<S, выполняется неравенство |f(x)-A|<E Бесконечно малая величина Последовательность Функция называется бесконечно малой в окрестности точки Функция
называется бесконечно
малой на бесконечности,
если
Также
бесконечно малой является функция,
представляющая собой разность функции
и её предела, то есть если
7. Первый и второй замечательные пределы. Два замечательных предела 1) lim(x0)sin/x=1 2) Явл. обобщением известного предела о посл-ти. Справедливо сл. предельное соотношение: lim(n)(1+1/n)^n=e (1) lim(n0)(1+x)^1/x=e (2) t=1/x => при х0 t из предела (2) => lim(x) (1+1/x)^x=e (3) Док-во 1)x+ n x:n=[x] => nx<n+1 => 1/(n+1)<1/x<1/n Посколько при ув-нии основания и степени у показательной ф-ции, ф-ция возрастает, то можно записать новое неравенство (1/(n+1))^n(1+1/n)^x (1+1/n)^(n+1) (4) Рассмотрим пос-ти стоящие справа и слева. Покажем что их предел число е. Заметим (х+, n) lim(n)(1+1/(n+1))=lim(n)(1+1/(n+1))^n+1-1= lim(n)(1+1/(n+1))^n+1lim(n)1/(1+1/(n+1))=e lim(n)(1+1/n)^n+1= lim(n)(1+1/n)^n lim(n)(1+1/n)=e1=e 2) x-. Сведем эту ситуацию к пред. Случаю путем замены переменной y=-x => y+, при x-. lim(x-)(1+1/x)^x=lim(y+)(1-1/y)^-y= lim(y+)((y-1)/y)^y=lim(y+)(1+1/(y-1))^y=e 3) Пусть x произвольным образом это означает при любом любом выборе посл-ти xn сходящихся к мы должны иметь в силу (3) соотношение lim(x)(1+1/xn)^xn=e (5) Условие 5~3, т.е расшифровка 3 на языке посл-ти. Выделим из посл-ти xn 2 подпосл-ти: {x‘n}+, {x‘‘n}-. Для каждой посл-ти по доказанному в п.1 и п.2 справедливо предельное соотношение 5 если заменить xnx‘nx‘‘n. По т-ме о связи
11. Понятие дифференцируемой функции. Производная суммы, произведения, частного, сложной и обратной функции. Уравнение касательной. Центральная идея диффер. ф-ций явл-ся изучение гладких ф-ций (без изломов и р-рывов кривые) с помощью понятия пр-ной или с помощью линейных ф-ций y=kx+b обладает простейшими наглядн. ф-циями; у=k‘ => k>0 то у возр. при всех х, k<0-то у убыв. при всех х, k=0 – ф-ция постоянна Теорема 20.2 . Производная суммы (разности) двух функций равна сумме (разности) производных этих функций: (u±ν)'=u'±ν'.Обозначим у=u±ν. По определению производной и основным теоремам о пределах получаем:
Теорема 20.3 . Производная произведения двух функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго: (u•ν)'=u'ν+v'u.
т е. (u•ν)'=u'•ν+u•ν'.При доказательстве теоремы использовалась теорема о связи непрерывности и дифференцируемости: так как функции u=u(х) и ν=ν(х) дифференцируемы, то они и непрерывны, поэтому ∆ν→0 и ∆u→0 при ∆х→0. Теорема
20.4.
Производная частного двух функций
Пусть у=u/v. Тогда
Производная сложной и обратной функцийПусть у=ƒ(и) и u=φ(х), тогда у=ƒ(φ(х)) — сложная функция с промежуточным аргументом u и независимым аргументом х.Теорема 20.5 . Если функция u=φ(х) имеет производную u'х в точке х, а функция у=ƒ(u) имеет производную у'u в соответствующей точке u=φ(х), то сложная функция у=ƒ(φ(х)) имеет производную у'х в точке х, которая находится по формуле у'х=у'u-u'х. Итак, для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножыть на производную промежуточного аргумента по независимому аргументу 14.Первое достаточное условие экстремума. Наибольшее и наименьшее значения функции на отрезке. Второе достаточное условие экстремума. Первое условие. Теорема. Если в достаточной близости от точки х = а производная f '(х) положительна слева от а и отрицательна справа от а (рис. 8), то в самой точке х = а функция f(x) имеет максимум при условии, что функция f(x) здесь непрерывна 1). Если, наоборот, слева от а производная f(х) отрицательна, а справа положительна (рис. 9), то f (х) имеет в точке а минимум при условии, что она здесь непрерывна 2). Теорема выражает тот факт, что f(x) при переходе от возрастания к убыванию имеет максимум, а при переходе от убывания к возрастанию -- минимум. 1) Однако, f(x) может и не быть дифференцируемой при х = а (см. рис. 2). 2) Однако, f(x) может и не быть дифференцируемой при х = а второе условие. Т е о р е м а 1. Пусть в точке х = а первая производная f ' (х) обращается в нуль; если при этом вторая производная f " (а) отрицательна, то функцияf (х) имеет в точке х = а максимум, если положительна, то -- минимум. В случае f "(а) = 0 см. теорему 2. Второе условие следующим образом связано с первым. Будем рассматривать f "(х) как производную от f '(х). Соотношение f "(а) < 0 означает, что f '(х) убывает в точке х = а. Атак как f '(а) = 0, то f(х) положительна при х < а и отрицательна при х > а. Значит (§ 3), f(х) имеет максимум при х = а. Аналогично для случая f " (а) > 0. Т е о р е м а 2. Если в точке х = а, где первая производная равна нулю, ближайшая не равная нулю производная имеет четный порядок 2k, то функция f (х) имеет при х = а максимум, когда f (2k)(а) < 0, и минимум, когда f(2k) (а) > 0. Если же ближайшая не равная нулю производная имеет нечетный порядок 2k + 1, то функция f(х) в точке а не имеет экстремума; она возрастает, когда f (2k + 1) (а) > 0, и убывает, когда f (2k + 1) (а) < 0. Значение, которое функция принимает в какой то точке множества, на котором задана данная функция, называется наибольшим (наименьшим) в данном множестве, если не существует другой точки этого множества, функция не имеет большего (меньшего) значения. Наименьшее и наибольшее значения функции, заданной на отрезке, могут достигаться либо в точках, в которых производная равна 0, либо в точках, в которых ее не существует, или же на концах отрезка. Непрерывная функция, которая заданна на отрезке, в любом случае достигает на нём наибольшего и наименьшего значений; если же непрерывную функцию рассматривать на интервале, то среди значений на данном интервале, наибольшего или наименьшего может попросту не оказаться.
|
4Свойства бесконечно малых величин. Связь бесконечно малых величин с пределами функций. Бесконечно большие величины. Свойства бесконечно малых 1.Сумма конечного числа бесконечно м.алых — бесконечно малая. 2Произведение бесконечно малых — бесконечно малая. 3.Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая. Если Отношение бесконечно малых величин образует так называемую неопределённость .0/0 Определения Допустим,
у нас есть бесконечно малые при одном
и том же
1.Если
2.Если
3.Если
Это обозначается как 4.Если
Для вычисления подобных пределов удобно использовать правило Лопиталя. Бесконечно большая величина Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция Последовательность Функция называется бесконечно большой в окрестности точки Функция
называется бесконечно
большой на бесконечности,
если
8. Непрерывность функции в точке и на множестве. Непрерывность справа и слева.
Опр. f(x) непрерывны Х0 и при этом ее предел в этой т-ке сущ-ет и равен знач. ф-ции в этой т-ке, т.е. lim(xx0)f(x)=f(x0)-непрерывность ф-ции в т-ке. Из определения вытекает что в случае непрерывности ф-ции в данной т-ке вычитание пределов сводится к вычит. знач. ф-ции в данной т-ке. Равенство lim(xx0)x=x0 (1‘). Т.е знак предела у непрерывной ф-ции можно вносить в аргумент ф-ции. Геометрически непрерывность ф-ции в т-ке х0 означает что ее график в этой т-ке не имеет разрыва. Если обозначить через у приращение ф-ции, т.е. у=f(x0+x)-f(x0) (приращение ф-ции в т. х0). “” - символ приращения. Приращение аргумента в т-ке х0 это соответствует тому, что текущая т. х, то условие непрерывности в т-ке х0 записывается сл. образом lim(x0)y=0~ у0 (1‘‘). Если в т-ке х0 ф-ция непрерывна, то приращение ф-ции 0 приращение аргумента. f(x) непрерывна в т-ке х0 <> y0 при х0. Если понятие предела приводит к понятию непр. Ф-ции то понятие одностороннего предела приводит к понятию односторонней непр. точки. Опр. Если f(x) имеет предел справа в т-ке х0(=f(x0+)) и этот предел равен значению ф-ции ф-ции в т-ке х0, т.е. f(x0+)=lim(xx0,x>x0)f(x)=f(x0), то ф-ция f(x) наз-ся непр. справа в т-ке х0. Аналогично при вып-нии усл. f(x0-)=lim(xx0, x<x0)f(x)=f(x0), то ф-ция наз-ся непр. слева в т. х0. Ясно что справедлива сл.теорема вытекающая из связи односторонних пределов ф-ция f(x) непр. в т-ке х тогда, когда она непр. в этой т-ке, как справа, так и слева. f(x0-)=f(x0+)=f(x0) Опр. Ф-ция f(x) непрерывна на некотором пр-ке D, если в каждой т-ке этого пр-ка при этом, если пр-ток D содержит граничную т-ку, то будем подразумевать соотв. одностор. непр. ф-ции в этой т-ке.
Теорема 20.6 . Если функция у=ƒ(х) строго монотонна на интервале (a;b) и имеет неравную нулю производную ƒ'(х) в произвольной точке этого интервала, то обратная ей функция х=φ(у) также имеет производную φ'(у) в соответствующей точке, определяемую равенством
Таким образом, производная обратной функции равна обратной величине производной данной функции. частная производная — одно из обобщений понятия производной на случай функции нескольких переменных. В явном виде частная производная функции
Определение. Пусть дана функция f, которая в некоторой точке x0 имеет конечную производную f(x0). Тогда прямая, проходящая через точку (x0; f(x0)), имеющая угловой коэффициент f ’(x0), называется касательной. Уравнение касательной Всякая невертикальная прямая задается уравнением вида y = kx + b, где k — угловой коэффициент. Касательная — не исключение, и чтобы составить ее уравнение в некоторой точке x0, достаточно знать значение функции и производной в этой точке.
Итак, пусть дана функция y = f(x), которая имеет производную y = f ’(x) на отрезке [a; b]. Тогда в любой точке x0 ∈ (a; b) к графику этой функции можно провести касательную, которая задается уравнением:
y = f ’(x0) · (x − x0) + f(x0)
Здесь f ’(x0) — значение производной в точке x0, а f(x0) — значение самой функции.
15.Выпуклые (вогнутые) функции одной переменой. Необходимое и достаточное условия точки перегиба. Асимптоты. Введем обозначение: x=(x1,x2,:,xn) - n-мерный вектор. Определение: n мерная функция f(x), определенная на выпуклом множестве D, называется выпуклой функцией тогда и только тогда, когда для любых двух точек x(1) и x(2) принадлежащих D, и любого числа L (0<=L<=1) выполняется неравенство: f(Lx(1) +(1-L)x(2))<=Lf(x(1))+(1-L)f(x(2)) Свойства выпуклых функций: 1.Хорда, соединяющая две любые точки кривой графика выпуклой функции, всегда проходит над (или выше) кривой в 2.интервале между двумя этими точками. 3.Выпуклая функция лежит над своими касательными 4.Тангенс угла наклона касательной, или первая производная f(x), возрастает или, по крайней мере, не убывает при увеличении x. 5.Вторая производная f(x) всегда не отрицательна на рассматриваемом интервале. 6.Для выпуклой функции локальный минимум всегда является глобальным минимумом. Функция f(x1,:,xn) является вогнутой функцией на множестве D тогда и только тогда, когда -f(x) есть выпуклая функция на D. Необходимое условие точки перегиба Теорема. Пусть функция y = f (x) дважды непрерывно дифференцируема на интервале (a, b). Для того, чтобы точка М(x0, f(x0)) была точкой перегиба графика функции y = f (x) необходимо, чтобы f " (x0) = 0. Достаточное условие точки перегиба Теорема. Пусть функция y = f (x) имеет вторую производную f "(x) в некоторой достаточно малой окрестности точки x0 интервала (a, b), за исключением, быть может самой точки х0, а график функции имеет касательную в точке С = (х0, f (x0)). Если при переходе через точку х0 вторая производная f "(x) меняет знак, то точка С является точкой перегиба графика функции y = f (x). Определение. Прямая называется асимптотой кривой, если расстояние от переменной точки кривой до этой прямой при удалении точки в бесконечность стремится к нулю. Вертикальные
асимптоты.Из
определения асимптоты следует, что
если Отметим, что горизонтальные асимптоты являются частным случаем наклонных асимптот при k =0.
|

 есть бесконечно малая функция в этой
же точке.
есть бесконечно малая функция в этой
же точке. ,
это означает, что
,
это означает, что K > 0) (
K > 0) ( δ = δ(K)>
0) (
δ = δ(K)>
0) ( 0 < |
x - x0
|
< δ ) : |
f
(x)
| > K
.
0 < |
x - x0
|
< δ ) : |
f
(x)
| > K
.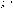 .
.
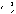 ,
тогда
,
тогда ε > 0) (
ε > 0) ( δ = δ(ε)> 0) (
δ = δ(ε)> 0) ( 0 < | x
- x0
|
< δ ) : 1/|
f
(x)|
<ε .
0 < | x
- x0
|
< δ ) : 1/|
f
(x)|
<ε .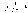 .
. ,
то:
,
то: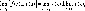 2)
предел
произведения функций равен произведению
пределов сомножителей,
т.е.
2)
предел
произведения функций равен произведению
пределов сомножителей,
т.е.

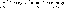
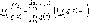 Теорема
3 (о
пределе сложной функции). Если
существует конечный предел
Теорема
3 (о
пределе сложной функции). Если
существует конечный предел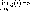
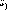 ,
то
,
то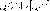
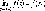 ,
то функция называется непрерывной
справа.
,
то функция называется непрерывной
справа.
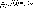 ,
то функция называется непрерывной
слева.
,
то функция называется непрерывной
слева.

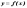 ,
определенную на некотором промежутке
,
определенную на некотором промежутке
 . Вычислим производную
. Вычислим производную
 ,
которая также является функцией на
,
которая также является функцией на
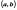 .
Производной второго порядка от функции
.
Производной второго порядка от функции
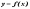 называется производная от ее
производной:
называется производная от ее
производной:
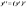 .
Аналогично определяют производную
любого порядка:
.
Аналогично определяют производную
любого порядка:
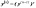
 называетсяправосторонним
пределом
(правым
пределом,
пределом
справа)
функции
называетсяправосторонним
пределом
(правым
пределом,
пределом
справа)
функции
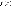 в точке
в точке
 ,
если для всякого положительного числа
,
если для всякого положительного числа
 отыщется отвечающее ему положительное
число
отыщется отвечающее ему положительное
число
 такое, что для всех точек
такое, что для всех точек
 из интервала
из интервала
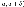 справедливо неравенство
справедливо неравенство
 .
.
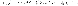
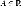 называется левосторонним
пределом
(левым
пределом,
пределом
слева)
функции
называется левосторонним
пределом
(левым
пределом,
пределом
слева)
функции
 в точке
в точке
 ,
если для всякого положительного числа
,
если для всякого положительного числа
 отыщется отвечающее ему положительное
число
отыщется отвечающее ему положительное
число
 такое, что для всех точек
такое, что для всех точек
 из интервала
из интервала
 справедливо неравенство
справедливо неравенство
 .
.
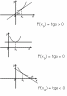

 xf(x0+
xf(x0+ x)−f(x0)=tg
x)−f(x0)=tg ,
где
,
где
 - угол наклона секущей AB.
Таким образом, разностное отношение
равно угловому коэффициенту секущей.
Если зафиксировать точку A
и двигать по направлению к ней точку
B,
то
- угол наклона секущей AB.
Таким образом, разностное отношение
равно угловому коэффициенту секущей.
Если зафиксировать точку A
и двигать по направлению к ней точку
B,
то
 x
неограниченно уменьшается и приближается
к 0, а секущая АВ
приближается к касательной АС.
Следовательно, предел разностного
отношения равен угловому коэффициенту
касательной вточкеA.
Отсюдаследует:производная
функции в точке есть угловой коэффициент
касательной к графику этой функции в
этой точке.
x
неограниченно уменьшается и приближается
к 0, а секущая АВ
приближается к касательной АС.
Следовательно, предел разностного
отношения равен угловому коэффициенту
касательной вточкеA.
Отсюдаследует:производная
функции в точке есть угловой коэффициент
касательной к графику этой функции в
этой точке. называется возрастающей
на интервале
называется возрастающей
на интервале
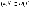 ,
если для любых двух точек
,
если для любых двух точек
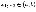 из неравенства
из неравенства
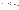 следует, что
следует, что
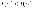 ;
убывающей
на интервале
;
убывающей
на интервале
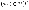 ,
если из неравенства
,
если из неравенства
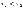 следует, что
следует, что
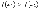 ;
невозрастающей
на интервале
;
невозрастающей
на интервале
 ,
если из неравенства
,
если из неравенства
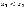 следует, что
следует, что
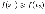 ,
и неубывающей
на интервале
,
и неубывающей
на интервале
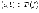 ,
если из неравенства
,
если из неравенства
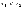 следует, что
следует, что
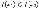 .
.
 и
и
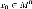 —
внутренняя точка области определения
—
внутренняя точка области определения
 называется пределом
числовой последовательности
называется пределом
числовой последовательности
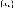 ,
если последовательность
,
если последовательность
 является бесконечно малой, т. е. все
её элементы, начиная с некоторого, по
модулю меньше любого заранее взятого
положительного числа.
является бесконечно малой, т. е. все
её элементы, начиная с некоторого, по
модулю меньше любого заранее взятого
положительного числа.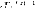 либо
либо
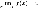 .
.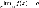 ,
то
,
то


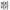 если ν(х)≠0 равна дроби, числитель
которой есть разность произведений
знаменателя дроби на производную
числителя и числителя дроби на
производную знаменателя, а знаменатель
есть квадрат прежнего знаменателя:
если ν(х)≠0 равна дроби, числитель
которой есть разность произведений
знаменателя дроби на производную
числителя и числителя дроби на
производную знаменателя, а знаменатель
есть квадрат прежнего знаменателя:


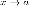 величины
величины
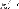 ,
то
,
то
 ,
то
,
то
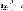 (предел конечен и не равен 0), то
(предел конечен и не равен 0), то
 (предел конечен и не равен 0), то
бесконечно малая величина
(предел конечен и не равен 0), то
бесконечно малая величина
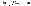 либо .
либо .
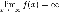
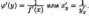
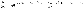
 или
или
 или
или
 ,
то прямая х = а – асимптота кривой y =
f(x)
,
то прямая х = а – асимптота кривой y =
f(x)