Замечание.
Под неконсервативными силами следует понимать силы, работа которых ведёт к рассеянию механической энергии, её переходу в другие формы энергии, например, во внутреннюю (тела нагреваются). Рассеяние (диссипация) механической энергии происходит, в частности, под действием различного рода сил трения, сопротивления движению. Эти силы объединяются общим термином – силы диссипативные.
Внутреняя энергия
это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутренняя энергия является однозначной функцией состояния системы.
Закон сохранения механической энергии.
Непосредственно из доказанной теоремы (4) следует, что механическую энергию можно считать постоянной, если пренебрежимо мала работа диссипативных сил. Причём, неважно, являются эти силы внутренними или внешними по отношению к телам, включённым в систему.
Формулировка закона сохранения механической энергии для замкнутой системы: Механическая энергия замкнутой системы тел, между которыми действуют
только консервативные силы, остаётся постоянной.
2,14 Понятие момент импульса
Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическай величина, определемая векторным произведением:
L=[r,mv]
Где : r – радиус-вектор, проведенный из точки О в точку А, p=mv –импульс материальной точки
L псевдовектор, направление которого совпадает с направлением поступательного движения правого винта приего вращении от r к p
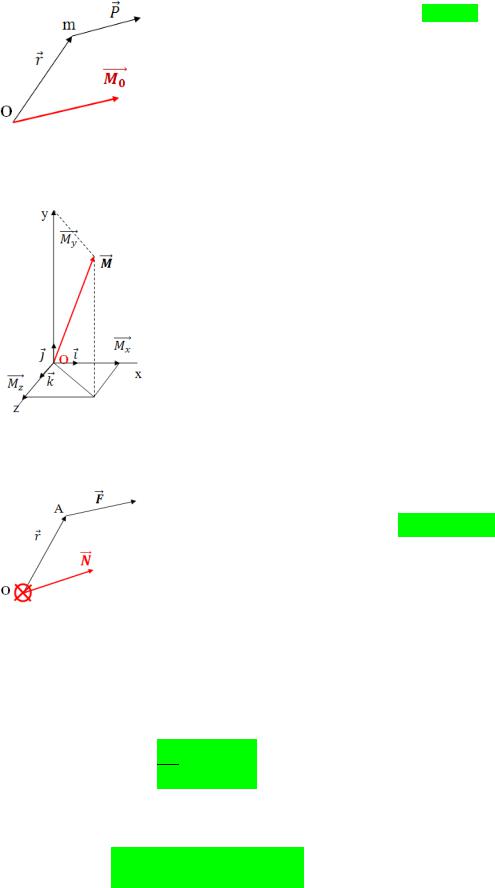
Определение .
[ ]
Векторное произведение радиуса-вектора, проведённого из т. О в материальную точку с импульсом .
Проекции на оси координат. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
( |
|
|
[ ] | |
| |
( |
) |
( |
) |
) |
|
|
|
|
( ̇ |
̇) |
|
|
|
|
|
|
|
|
( |
̇ |
̇) |
|
|
|
|
|
|
( |
̇ |
̇) |
|
|
Понятие момента силы
Определение.
Моментом силы ( ) относительно т. О называется:
( ) 
[ ]
радиус-вектор, проведённый из т. О в точку приложения силы (А). Проекции момента силы на декартовы оси координат с центрами в т. О:
; ;
Теорема об изменении момента импульса
Формулировки: |
В дифференциальной форме. |
|
∑ ( ) |
В интегральной форме.
|
|
∫ |
(∑ ( )) |
Производная по времени от момента импульса системы материальных точек равна сумме моментов внешних сил, приложенных к точкам системы.
Краткое название теоремы – уравнение моментов.
Приращение момента импульса системы равно импульсу суммарного момента внешних сил за соответствующий промежуток времени
Для одной материальной точки
Запишем определение момента импульса |
|
|
|
|
|
|
||
|
|
|
|
|
[ ] |
|||
Продифференцируем по времени |
|
|
|
|
|
|
||
|
|
[ |
|
|
] [ |
|
] |
|
|
|
|
|
|
|
|||
Преобразуем, учитывая, что
по определению скорости
по II закону Ньютона
сумма сил, действующих на выделенную материальную точку со стороны тел, не включённых в
систему.
сума сил, действующих на выделенную точку со стороны других тел, входящих в систему.
|
[ ] |
[ ] |
( ) |
( ) |
|
[ ] |
( ) |
[ ] равно нулю по свойству векторного произведения.
Итак, производная момента импульса материальной точки равна сумме моментов всех сил, приложенных к этой точке.
Для системы
Для каждой точки системы справедливо (1)
|
|
|
( ) |
( ) ( ) |
|
|
|
|
|
||
|
|
|
|
||
Суммируем (2) по всем телам системы |
|||||
∑ |
|
|
∑ ( ) |
∑ ( ) ( ) |
|
|
|||||
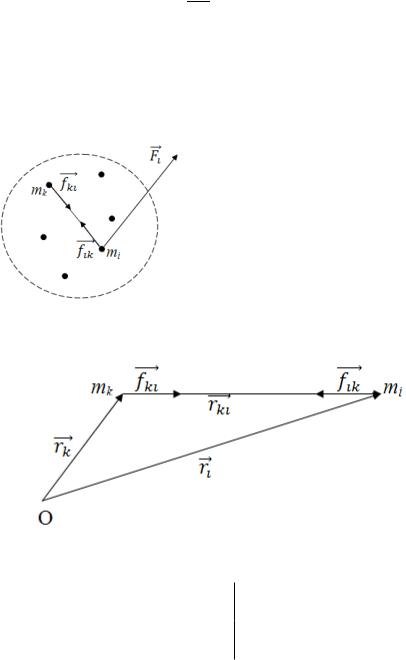
Покажем, что сумма моментов внутренних сил равна нулю.
Для двух точек:
|
∑ ( ) |
[ ] [ ] |
По III з-ну Ньютона |
[ ] |
[ ] |
По правилу сложения векторов |
[( ) ] |
|
|
|
|
[ ] |
|
|
|
|
||
Аналогично для любой другой пары тел системы. |
|
|
|
|||||
Т.о., для момента импульса системы получим |
|
|
|
|||||
|
|
|
|
∑ |
( ) |
( |
) |
|
Интегрируя (4), получаем |
|
|
|
|||||
|
|
|
||||||
|
|
|
|
|
|
|
||
|
|
|
∫ (∑ ( )) |
( ) |
||||
Закон сохранения момента импульса.
Из доказанной теоремы непосредственно следует закон сохранения момента импульса. Момент импульса замкнутой системы остаѐтся
постоянным |
|
|
, если |
Замечание.
Момент импульса может сохраняться и в незамкнутой системе, если внешние силы не создают момента. Характерный пример: движение частицы (тела) в центральном поле сил.
В центральном поле на материальную точку m действует сила , направленная к центру. Момент этой силы относительно центра сил (т.О.) равен [ ] , т.к. и лежат на одной прямой. Из уравнения моментов следует
|
, |
|
|
2,15 Oднородность времени и закон сохранения энергии
Вывод этого утверждения может быть произведѐн, например, на основе лагранжева формализма[1]. Если время однородно, то функция Лагранжа, описывающая систему, не зависит явно от времени, поэтому полная еѐ производная по времени имеет вид:
Здесь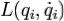 
— функция Лагранжа, 
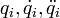— обобщѐнные координаты и их первые и вторые производные
по времени соответственно. Воспользовавшись уравнениями Лагранжа, заменим производные |
на выражение |
:
Перепишем последнее выражение в виде
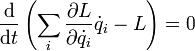
Сумма, стоящая в скобках, по определению называется энергией системы и в силу равенства нулю полной производной от неѐ по времени она является интегралом движения (то есть сохраняется).
Bзотропность пространства и закон сохранения момента импульса
Изотропность — одно из ключевых свойств пространства в классической механике. Пространство называется изотропным, если поворот системы отсчета на произвольный угол не приведет к изменению результатов измерений.
Связь закона сохранения момента импульса с изотропностью пространства. Под изотропностью пространстав понимается эквивалентность различных направлений в пространстве. Это означает, что если имеется некоторая изолированная физическая система, то развитие событий в ней зависитот того, как она ориентирована в пространстве. В применениии к изилированной системе материальных точек отсюда следует, что угловое перемещение системы на δφ не изменит еѐ внутреннего состояния и его внутренних движений. Поэтому полная работа внутренних сил при угловом перемещении должна быть равна нулю. При угловом перемещении δφ материальная точка, характеризуемая радиусом вектором ri , испытывает смещение δri =δφ*ri. Равенство нулю полной работы внутренних сил при угловом перемещении системы на δφ выражается в виде
½*∑∑(δri∙Fji+δri∙Fij)=0. (1)
Следовательно можно написать:
δri∙Fji+δri∙Fij=(δφ´ri)∙Fji+( δφ´ri)∙Fij=δφ∙(ri´Fji)+δφ´(ri´Fij)=δφ∙[(ri-rj)´Fji], (2)
где во внимание известное из векторной алгебры правило о циклической перестановке сомножетелей в смешанном векторном произведении и третий закон Ньютона. Пожставляя (2) в (1), находим ½*∑i∑jδφ∙[(ri-rj)*Fji]=0. Поскольку угловое перемещение δφ произвольно, получаем равенство ∑i∑j(ri- rj)*Fji=0. Можно сказать, что полученное равенство следует из изотропности пространства. А это означает, что закон сохранения момента импульса изолированной системы материальных точек обусловлен фундаментальным свойством пространства в инерциальных система — его изотропностью.