Теория_игр_методичка

Теория игр

и

исследование

операций

Методические указания к выполнению задания студентам экономических специальностей РГСУ

2

1. Построение математических моделей простейших экономических задач.

В самых разных областях экономической и управленческой деятельности приходится решать задачи, суть которых заключается в выборе из многих возможных вариантов. Здравый смысл подсказывает нам, что нужно остановиться на самом наилучшем из всех вариантов. Наилучший или, как обычно говорят, оптимальный вариант отвечает двум требованиям. Во-первых, он является одним из допустимых и, вовторых, обеспечивает максимум или минимум (по смыслу) поставленной цели. Именно эти соображения легли в основу целого ряда исследований в области так называемого

математического программирования.

Совокупность условий деятельности управляемого объекта записывается в виде системы уравнений и неравенств, которая определяет множество допустимых вариантов его поведения и называется системой ограничений. Выбор оптимального варианта осуществляется с помощью так называемой целевой функции (например, максимум прибыли, минимум затрат, минимум времени, максимум произведенной продукции и т.д.). Если сформулирована система ограничений и целевая функция, считается, что задача поставлена (другими словами, построена математическая модель объекта исследования). Для решения подобных задач, как правило, нереально просто перебрать все допустимые варианты и выбрать из них наилучший из-за того, что их число бесконечно или практически необозримо. Методы оптимизации представляют собой алгоритмы для решения определенных классов подобных задач.

Если система ограничений и целевая функция задачи математического программирования линейны, то есть представляют собой уравнения и неравенства первой степени, то мы имеем дело с задачей линейного программирования. Требуется найти максимальное (или минимальное) значение функции

		n
F( x 1 ,x 2 ,...x n ) ci x i			(1)
при ограничениях		i 1
n
aij x i bj ,		j 1,2,...m	(2)
i 1
x i 0	,	i 1,2,...n

Решение, удовлетворяющее (2), при котором функция (1) принимает максимальное (минимальное) значение, называется оптимальным решением.

Пример 1. Задача распределения ресурсов.

Мебельная фабрика изготавливает диваны и шкафы. На изготовление одного дивана требуется 3 кв. метра материи для обивки и 0.08 кубометров деревянных досок. Средние затраты трудовых ресурсов при этом – 0.8 человекодней. Для изготовления одного шкафа же необходимо 4 кв. метра древесностружечной плиты, и 0.1 кубометров деревянных досок. Средние затраты трудовых ресурсов при этом – 0.5 человекодней. В наличии на фабрике имеется 4800 кв. метров древесностружечной плиты, 6000 кв. метров материи и 200 кубометров досок. Можно использовать 2000 человекодней трудовых ресурсов. Сколько нужно изготовить шкафов и диванов для получения наибольшей выручки от их продаж, если диван стоит 1600 руб., а шкаф – 1000 руб.

Составим математическую модель задачи. Пусть x1 – количество изготовленных диванов, а x2 – шкафов. Тогда общая выручка выражается следующей целевой функцией, которая должна принимать максимальное значение в оптимальном варианте:

F( x1 ,x 2 ) 1600x1 1000x 2 ,

(3)

								3
а система ограничений (1.2) принимает вид
4x			2		4800
			1	6000
3x
						1 0.1x 2 200 ,		(4)
0.08x
						0.5x 2	2000
0.8x1
x	1	,x			2	0

Пример 2. Задача составления рациона (задача о диете).

При откорме каждое животное ежедневно должно получить не менее 9 единиц питательного вещества 1-го вида, не менее 8 единиц вещества 2-го вида и не менее 12 единиц вещества 3-го вида. Для составления рациона используют два вида корма. Содержание количества единиц питательных веществ в 1 кг каждого вида корма соответственно равно 3, 1, 1 и 1, 2, 6. Стоимость 1кг корма 1-го вида – 4руб,, а второго

– 6 рублей. Необходимо составить дневной рацион нужной питательности, причем затраты на него должны быть минимальными.

Для составления математической модели задачи обозначим через x1 и x2

соответственно количество килограммов корма-1 и корма-2 в дневном рационе. При составлении рациона нужно добиться того, чтобы затраты были минимальны. Общие затраты выражаются целевой функцией

F( x1 ,x 2 ) 4x1 6x 2 .

(5)

Принимая во внимание, что количество единиц в дневном рационе не должно быть меньше предусмотренного, можно получить систему ограничений:

3x	1 x 2	9
	2x 2	8
x 1			(6)
	6 x 2
x 1		12
	,x 2 0
x 1

Рассматривая приведенные задачи и подобные им, нетрудно заметить, что, если потребовать, чтобы ресурсы использовались полностью, то соответствующее ограничение выражается в виде уравнения, а не неравенства.

2.Графический способ решения задач оптимизации.

Приведенным примерам можно дать адекватную геометрическую интерпретацию. Так, каждое из ограничений типа неравенства представляется множеством точек полуплоскости, лежащей по одну из сторон соответствующей прямой. Пересечение всех полуплоскостей образует некоторую область, называемую многоугольником решений. Совокупность точек полученной области есть совокупность допустимых решений задачи. Если в задаче n 3 , можно говорить о трехмерном многограннике решений и т.д.

Таким образом, геометрически задача линейного программирования представляет собой отыскание такой точки многогранника решений, координаты которой доставляют линейной целевой функции минимальное значение.

Заметим, что область допустимых решений – выпуклое множество точек, оно содержит вместе с любыми двумя точками и соединяющий их отрезок (по определению выпуклости).

В тех случаях, когда в задаче всего лишь две переменные, можно использовать графический метод решения. Данный метод также можно применять в некоторых трехмерных задачах.

				4
Решение типового примера
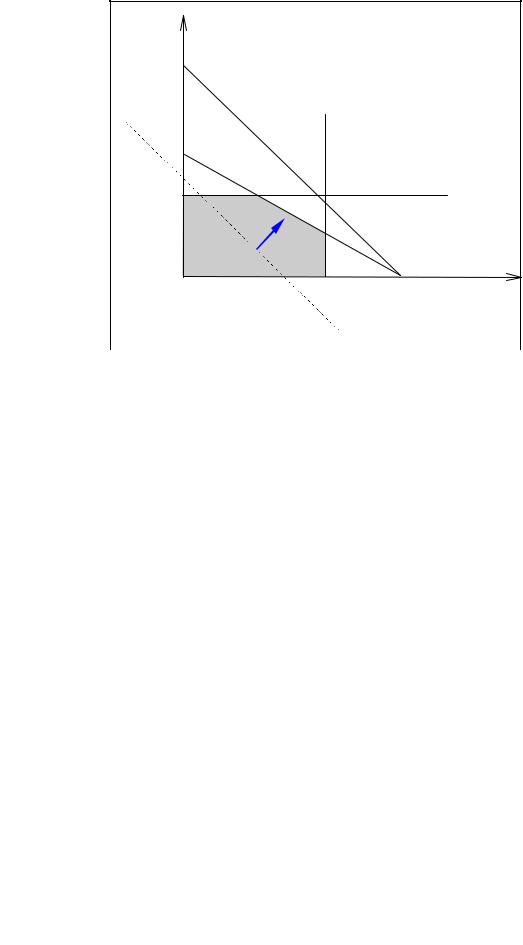
В качестве примера рассмотрим задачу об оптимальном распределении ресурсов из
(3–4). Построим область, удовлетворяющую неравенствам-ограничениям. На рисунке –
				это фигура OABCD.
				Координаты вершин
	x2			области нетрудно найти как
				точки пересечения соответ-
4000				ствующих прямых:
				O( 0;0) , A( 0;1200) ,
				B( 1000;1200) , C( 2000;400) ,
				D( 2000;0) .
2000				Поставленной задаче
	B			линейного программирования
1200				можно дать следующую
A				интерпретацию. Найти точку
	C			многоугольника решений,
				которая лежит на прямой
O		2500		1600x 1 1000x 2 const и
	2000		x1	функция F( x 1 ,x 2 ) в ней
	D
				достигает максимума.
				Построим прямую
				1600x 1 1000x 2 0 . Она
пересекает область допустимых решений в точке O, целевая функция в ней минимальна и
принимает значение, равное нулю. Значения			F( x 1 ,x 2 )	возрастают в направлении вектора
grad F( x 1 ,x 2 ) ( 1600;1000) , поэтому, передвигая построенную прямую в направлении
этого вектора параллельно самой себе, получим, что максимума целевая функция
достигает в точке C. Оптимальным решением, соответственно, будет x 1 2000;x 2 400 .

Замечание 1. Если решается задача на минимум (например, задача о диете), прямую передвигать, очевидно, следует в направлении, противоположном направлению вектора градиента.

Замечание 2. Решение (не обязательно оптимальное), соответствующее одной из вершин многоугольника, задает так называемый опорный план. Процесс решения можно представить как передвижение от одного опорного плана к другому с последовательным “улучшением” значения целевой функции. Оптимальное решение не всегда достигается в одной из вершин многоугольника. Так, если область допустимых решений неограниченна в сторону возрастания целевой функции, решения не существует. Если прямая параллельна той стороне многоугольника, где достигается максимум, существует бесконечное число решений, соответствующим точкам, лежащим на указанном отрезке– стороне многоугольника.

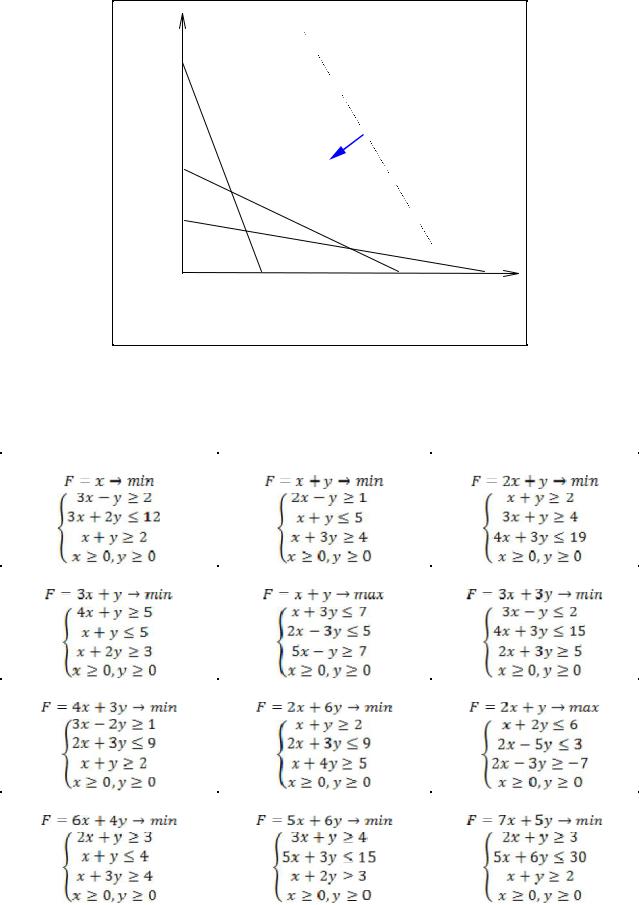
В качестве следующего примера рассмотрим задачу о диете из примера 2 (5–6). Построим область, удовлетворяющую неравенствам-ограничениям. На рисунке – это бесконечная фигура, ограниченная осями координат и ломаной ABCD.

В этом случае целевая функция уменьшается в направлении, противоположном направлению градиента (на рисунке это направление показано стрелкой). Очевидно, что

своего минимума функция достигает в точке B с координатами x1 2; x2 3 .

5

x2

9

A

4

B

2

C

D x1

O	3	8	12

Заданиена самостоятельнуюработу

Решить графически задачу линейного программирования

Вариант 1	Вариант 2	Вариант 3

Вариант 4	Вариант 5	Вариант 6

Вариант 7	Вариант 8	Вариант 9

Вариант 10	Вариант 11	Вариант 12

6

Вариант 13	Вариант 14	Вариант 15

Вариант 16	Вариант 17	Вариант 18

Вариант 19	Вариант 20	Вариант 21

Вариант 22	Вариант 23	Вариант 24

Вариант 25	Вариант 26	Вариант 27

Вариант 28	Вариант 29	Вариант 30

3.Решение задачи линейного программирования симплекс-методом

Таким образом, в любой задаче перебрав все опорные планы, можно выбрать из них оптимальный. Однако при больших m и n это очень трудно. Поэтому необходимо иметь схему, позволяющую за конечное число шагов достичь оптимального решения. Такой схемой является симплекс-метод, изобретенный в 1949 году Данцигом.

Пусть поставлена следующая задача линейного программирования: Найти минимальное значение функции

n
F( x 1 ,x 2 ,...x n ) ci x i	(7)
i 1

при ограничениях типа равенства

			7
n
aij x i	bj ,	j 1,2,...m	(8)
i 1
x i 0	,	i 1,2,...n

Данную задачу всегда можно получить из задачи (1–2) следующим способом:

1.) Если ищется решение, при котором целевая функция F1( x 1 ,x 2 ,...x n ) достигает

максимума, то очевидно, что для задачи на минимум достаточно взять ее с противоположным знаком.

2.) Неравенства в выражениях для ограничений нужно преобразовать в равенства введением неотрицательных дополнительных переменных, если к левой части неравенства типа «меньше или равно» прибавить неотрицательную переменную, а из левой части неравенства типа «больше или равно» вычесть неотрицательную переменную. При этом, конечно, каждый раз при проведении такой операции количество переменных увеличивается на единицу.

Решение типового примера

Рассмотрим задачу (3–4) из примера 1. Прежде всего, преобразуем систему ограничений

(4) к более удобному виду:

x	2	1200
		2000
x	1
			5x 2			10000	(4*)
4x 1
			5x 2			20000
8x 1
x	1	,x		2	0
Далее представим задачу как задачу поиска минимального значения функции
F( x 1 ,x 2 ) 1600x 1 1000x 2 .							(9)
Введем дополнительные переменные						x 3 ,x 4 ,x 5 ,x 6 так, что	система ограничений

представляется в виде

x	2	x 3				1200
		x 4				2000
x	1
			5x 2					x 5				10000
4x 1
			5x 2					x 6				20000
8x 1
x	1	,x		2	,x	3	,x		4	,x	5	,x	6	0

После этого выразим новые переменные через исходные из (10):

x 3		x 2	1200
	x 1		2000
x 4
	4x 1	5x 2	10000
x 5
	8x 1	5x 2	20000
x 6

(10)

(11)

Переменные в левой части этой системы называются базисными переменными, а в правой – свободными переменными. Таким образом, в данной задаче x 3 ,x 4 ,x 5 ,x 6 –

базисные переменные, которые выражаются через x 1 ,x 2 – свободные переменные. Тем самым задан начальный опорный план. Ему соответствуют нулевые значения x 1 ,x 2 и x 3 1200,x 4 2000,x 5 10000,x 6 20000 .

Составим соответствующую начальному опорному плану таблицу:

8

	x 1	x 2	свободные члены
x 3	0	1	1200
x 4	1	0	2000
x 5	4	5	10000
x 6	8	5	20000
F	1600	1000	0

Здесь во втором и третьем столбцах проставляются коэффициенты при свободных переменных в выражениях (1.11) с обратными знаками. Переход к следующему опорному плану осуществляется по такому правилу:

Прежде всего

выбирается ведущий столбец, то есть тот, у которого в последней строке содержится неотрицательный элемент (в нашем примере, допустим, второй столбец – он содержит коэффициенты при x 1 );

выбирается ведущая строка, для этого подсчитываются отношения свободных членов к положительным элементам ведущего столбца. Та строка, в которой это отношение

минимально, объявляется ведущей (в нашем примере это третья строка –

2000	2000,	10000	2500,	20000	2500 );
1		4		8

ведущий элемент, таким образом, находится на пересечении ведущей строки и ведущего столбца (в нашем примере он равен 1 и обведен в кружок);

Затем строится новая симплекс-таблица, у которой

базисная переменная и свободная переменная, находящиеся в ведущей строке и ведущем столбце соответственно, меняются местами;

ведущий элемент заменяется величиной, ему обратной ( 11 1 );

все остальные элементы ведущей строки, включая свободный член, заменяются их отношениями к ведущему элементу ( 01 0, 20001 2000 );

все элементы ведущего столбца, кроме ведущего элемента, заменяются их

отношениями к ведущему элементу, взятыми с обратными знаками

( 01 0, 14 4, 81 8, 16001 1600 );

остальные элементы таблицы заменяются по "правилу 4-х элементов": любой такой элемент умножается на ведущий и из произведения вычитается произведение двух других элементов, составляющих с первыми вершины прямоугольника, после чего

результат делится на ведущий элемент. (В нашем примере

1 1 0 0	1,	1200 1 2000 0	1200,	5 1 4 0	5,	10000 1 4 2000	2000 и так далее...).
1		1		1		1

Таким образом, следующая симплекс-таблица принимает вид:

9

	x4	x 2	свободные члены
x 3	0	1	1200
x1	1	0	2000
x 5	–4	5	2000
x 6	–8	5	4000
F	–1600	1000	–3200000

В графическом методе решения этой задачи (вспомним рисунок) полученный опорный план соответствует точке с координатами x1=2000, x2=0.

Следуя описанному алгоритму, продолжаем строить последовательность симплекстаблиц до тех пор, пока в последней строке не останется положительных элементов. Достижение такой ситуации означает достижение оптимального плана.

	x4	x 5	свободные члены
x 3	4/5	-1/5	800
x1	1	0	2000
x 2	–4/5	1/5	400
x 6	-4	-1	2000
F	-2400	-200	-3600000

Таким образом, мы достигли оптимального решения задачи x 1 2000;x 2 400 , при этом целевая функция принимает значение, равное 3600000.

Замечание 1. Полученное решение допустимо, так как неотрицательны элементы в последнем столбце симплекс-таблицы. Встречаются, однако, задачи, у которых, например, это условие не выполняется для начального опорного плана. Решать описанным симплексметодом подобные задачи нельзя, и используют так называемый двойственный симплекс-метод.

Замечание 2. Так же, как и при графическом методе решения, может не существовать оптимального плана. Если в последней строке (строке коэффициентов целевой функции) есть положительный элемент, но выбрать его ведущим нельзя, так как все его остальные элементы отрицательны. Оптимальное решение в этой задаче никогда не будет достигнуто.

Замечание 3. Так же, как и при графическом методе, оптимальное решение может быть не единственно. Если в последней строке (строке коэффициентов целевой функции) есть нулевой элемент, то это означает существование альтернативного решения. Его можно получить, выбрав ведущим указанный столбец. Такое же значение целевая функция принимает во всех точках отрезка, соединяющего точки, отвечающие найденным двум решениям.

10

Рассмотрим задачу (5–6) из примера 2.

Введем дополнительные переменные x3 , x4 , x5 так, что система ограничений представляется в виде

3x1 x2 x3 9x1 2x2 x4 8

x1 6x2 x5 12

x1 , x2 , x3 , x4 , x5 0

После этого выразим отсюда новые переменные через исходные:

x3x4x5

3x1 x2 9

x1 2x2 8

x1 6x2 12

Таким образом, в данной задаче x3 , x4 , x5 – базисные переменные, которые выражаются через x1 , x2 – свободные переменные. Тем самым задан начальный опорный план. Ему соответствуют нулевые значения x1 , x2 и x3 9, x4 8, x5 12 . Это

означает, что такой план не удовлетворяет условиям неотрицательности переменных, то есть мы находимся вне области допустимых решений.

Составим соответствующую начальному опорному плану таблицу:

	x1	x2	Свободные члены
x3	-3	-1	-9
x4	-1	-2	-8
x5	-1	-6	-12
F	-4	-6	0

В этом случае применим двойственный симплекс-метод, который отличается от описанного выше правилами выбора ведущего элемента. В остальном правила перехода к новому опорному плану и, соответственно, новой симплекс-таблице остаются такими же, как и раньше.

Прежде всего

ведущей строкой объявляется любая из строк с отрицательной базисной переменной;

для выбора ведущего столбца выделим в ведущей строке отрицательные элементы. Ведущим объявляется столбец, в котором абсолютная величина отношения коэффициентов целевой функции к отрицательным элементам ведущей строки является минимальной.

В нашем примере возьмем за ведущую первую строку (можно выбирать любую из трех). Ведущим столбцом объявляется первый, так как 43 16 .

Таким образом, следующая симплекс-таблица принимает вид: