14. Методические указания 2

Индивидуальное задание и его решение

ЛАиАГ). Другая линия – прямая, график которой расположен в полуплоскости положительных значений переменной х. Поэтому изобразим лишь одну ветвь гиперболы.

Фигура D симметрична относительно оси Ох и площадь её равна

2 £ x £ 3

SD = 2SD

=

удвоенной площади фигуры D1

:

£ y

£

x

2

- 4

0

1

3

x2 −4

3

3

= 2∫dx ∫dy = 2∫dx × y

0 x2 −4 = 2∫

x 2 - 4

dx =

2

0

2

2

xdx

u =

x 2 - 4 du =

= 2x

3 -

=

x 2 - 4

x 2 - 4

dv = dx v = x

2

3

x 2 dx

3

(x 2 − 4)+ 4

3

3

dx

− 2∫ x 2 − 4dx −8∫

− 2∫

= 6 5

− 2∫

dx = 6 5

.

2

x 2 − 4

2

x 2 − 4

2

2

x 2 − 4

Следовательно,

3

3

−8 ln(3 +

)+8 ln 2

4∫

x 2 − 4dx = 6

−8ln

x +

x 2 − 4

= 6

5

5

5

2

2

2

SD = 3 5 + 4 ln

» 2,86 .

3 +

5

Решение задачи 6

у

В случае,

когда область D является

частью круга или кольца, чаще всего удобно

перейти к полярной системе координат (см.

лекцию

14

ЛАиАГ).

Связь

между

Оp х декартовыми и полярными координатами

осуществляется согласно формулам

у

x2 − y 2 = 4

(63) (ЛАиАГ).

В данной ситуации

5

область D –

круг радиуса p, и

D

x = 3

намерение

перейти

к

полярным

координатам вызвано значительным

1

упрощением описания этой области

О

2

3

х

системой

неравенств

в

полярных

координатах

по сравнению с

- 5

0 £ j £ 2p

декартовыми:

.

D :

0 £ r £ p

Выразим подынтегральную функцию через полярные координаты:

1 -

y 2

= 1 -

r 2 sin 2 j

= 1 - tg 2j = 2 -

1

.

x2

cos2 j

r 2 cos2 j

118

Индивидуальное задание и его решение

Для вычисления двойного интеграла в полярных координатах воспользуемся формулой (50) (см. также П.47):

y

2

1

2π

π

1

2

2

2 −

2

∫∫ 1 −

x

dxdy = ∫∫ 2 −

cos

rdrdϕ = ∫dϕ∫

rdr =

D

D

ϕ

0

0

cos

ϕ

2π

2

π

π

2

1

r

(2ϕ −tgϕ)

2π

3

= ∫

2 −

dϕ

=

0

= 2π

≈ 62 .

2

0

cos

ϕ

2

0

2

Решение задачи 7

Сделаем чертёж и далее будем действовать как в примере 48.

у

Центр тяжести данной фигуры

определим

по

формулам

(54),

y 2 = 4x + 4

2

y 2 = −2x + 4

которые, в силу того, что плотность

постоянна,

приобретают

вид:

∫∫xdxdy

∫∫ydxdy

-1

О

2

х

=

=

c

D

,

c

D

. Следует

-2

1

∫∫dxdy

2

∫∫dxdy

D

D

также заметить, что полученная

фигура

симметрична

относительно

оси Ох, из чего можно сделать вывод, что c2 = 0 .

Найдём значение c1 . Опишем область D, как область второго типа:

		− 2 ≤ y ≤ 2																																			4−y2
																															2							2							2						4 − y 2								y 2	− 4
D : y 2 − 4				≤ x			≤				4 − y 2						∫∫dxdy = ∫dy																					∫dx = ∫																			−				dy =
																																																			2							4
																			D													−2					y2 −4									−2
		4											2
																																						4
				2					3y				2											y			3					2											8									8
		= ∫			3 −										dy = 3 y						−														=			3 2 −											+ 2 −									= 8		;
										4														12																			12									12
			−2																													−2
																	4 − y 2															(4 − y2 )2														(y2 − 4)2
													2					2						1					2
			∫∫xdxdy = ∫dy															∫xdx =											∫													−												dy =
																								2														4
			D											−2			y	2	−4																																16
																												−2
																		4
1		2	3y		4			3y				2									1					3y				5						y		3									2
		∫				−								+ 3 dy = =																				−					+ 3y												= 3,2 . Согласно
2			16							2											2						80								2
		−2																																													−2
																																						3,2
															формулам (54) c																				=					= 0,4 .
																															1							8

Решение задачи 8

119

Индивидуальное задание и его решение

Одно из приложений двойного интеграла – возможность вычисления объёма тела, боковой поверхностью которого является цилиндрическая поверхность (см. лекцию 15 ЛАиАГ). Например, если образующие этого тела параллельны оси Оz, основание D лежит в плоскости хОу, а сверху тело ограничено поверхностью z = f (x, y), то

искомый объём вычисляется по формуле: V = ∫∫ f (x, y)dxdy .

D

	z
6	y = 5

z = 3x

		О
			1				5 у
2
х					y =1 + x2
		0 ≤ x ≤ 2			. Тогда
D :		+ x2 ≤ y ≤ 5
1

Как следует из чертежа, полученное тело удовлетворяет всем условиям для применения

записанной формулы:				сверху
оно	ограничено		плоскостью
z = 3x ;		боковую	поверхность
образуют		параболический
цилиндр		y =1 + x 2	и плоскость
y = 5	параллельные			оси	Оz;
основание D лежит в плоскости
z = 0 .
	Опишем		область		D
системой			неравенств:

	2			5	2										2
V = ∫∫3xdxdy = ∫3xdx ∫dy = ∫3xdx × y											15+x2				= ∫3x(5 - (1 + x2 ))dx =
D	0	1+x2			0										0
	2		3				2		3x		4			2
	= ∫(12x −3x					6x		−							=12 .
				)dx =					4
	0													0

Решение задачи 9

Данный интеграл принадлежит к классу криволинейных

интегралов 2-го рода,

ориентированная кривая L

парметризована

cost

уравнениями

(t )=

,

а подынтегральная

вектор-функция

r

sin t

- y 2 x

. Применим формулу (41)

для вычисления

имеет вид: F (x, y)=

2

x

y

этого интеграла (см. также П.41), где

120

Индивидуальное задание и его решение

−sin t

π

- sin t

cos t

2

cos t

a = 0 , b =

, F (r (t ))=

,

r ′(t )=

cos t

2

cos t

sin t

2

sin t

(

(t ))×

¢(t )= -sin t

×

−

sin t

+ cos t

×

cos t

=

1

.

cos t

sin t

F

r

r

2 cos t

2 sin t

2

π

π

1

2

1

π ≈ 0,785.

∫x 2 ydy − y 2 xdx =

2

∫dt =

t

=

L

2

0

2

0

4

121

Индивидуальное задание и его решение

ОБРАЗЕЦ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ ПО ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ Задача 1

Решить дифференциальные уравнения:

1) y′e x = y ln 2 y ;

′

=

1 + y 2

2)

xtgydx − (x2 − 2)dy = 0 ;

9) y

1

− x2 ;

yy′′ = (y′)2 ;

′

x + y

10)

=

3)

y

;

y′′ = x

;

y − x

11)

y′

xy′ − y = (x − y)

;

2x

4)

ln(x − y) − ln x

12)

y′′ +

y′ = 2x ;

y

x2 +1

5)

xy′ = xe

+ y ;

x

13)

3xdy = ( y + 6x2 )dx ;

6)

y′cos x = −y sin x + 2x ;

14)

(4xy − 3)y′ + y 2 =1;

7)

x2 y′ − 2xy = 2x5 y ;

15)

x(ln y + 2ln x −1)dy = 2 ydx

8)

x( y′ + y) = e−x ;

(Ввести

замену

z = ln y + 2ln x −1).

Задача 2

Решить линейные однородные дифференциальные уравнения 2-го порядка:

1) y′′ − 3y′ + 2 y = 0 ;						5) y′′ − 3y′ + 8 y = 0 ;
2)	y′′ +16 y = 0 ;					6) y′′ − 3y′ = 0 ,	при
3)	y	′′	+ 7 y	′	= 0 ;	′
						y(1) = 2, y (1) =1;
4)	y′′ − 6 y′ + 9 y = 0 ;					7) y′′ + 2 y′ + 5 y = 0 , при
						′
						y(0) =1, y (0) = 3 .

Задача 3

Решить линейные неоднородные дифференциальные уравнения 2-го порядка:

1) y′′ − 25 y = 6e2 x ;		5) y′′ − 4 y′ = 4x +10 , при
	2	y(0) = 4,	′	= −7 ;
2) y′′ + 5 y′ + 6 y = x + 4 ;			y (2)

122

Индивидуальное задание и его решение

3) y′′ + 4 y = cos 5x ;			6)	y′′ − 2 y′ +1y = e x + sin x ;
4) y′′ + 6 y′ + 9 y = 4e−3x , при			7)	y′′ + 36 y = xe−7 x .
y(1) = 4e	−3	′
		, y (0) = 3 ;

Задача 4

Решить методом вариации произвольной постоянной:

		′′			1
	1) y		− 3y + 2 y = 2		+ e−x	;

2) y′′ − 25 y = 6e2 x

РЕШЕНИЕ ЗАДАЧ Решение задачи 1

1) Решить дифференциальное уравнение: y′e x = y ln 2 y .

2

Преобразуем данное уравнение: y′ = y ln y ; e x

Разделим переменные:

dy

=

y ln2 y

dy

=

dx

∫

dy

= ∫e−x dx .

dx

e

x

y ln

2

y

e

x

y ln

2

y

Вычислим первый интеграл:

∫

dy

=

ln y = t

= ∫

dt

=

∫t −2 dt = −t −1 + C = −

1

+ C ;

1

dy = dt

y ln2 y

t 2

ln y

y

Таким образом, получаем:

1

1

1

= −e−x + C

−x

−

ln y

=

y = e e

−C .

ln y

e

−x − C

2) Решить дифференциальное уравнение: xtgydx − (x2 − 2)dy = 0 .

Разделяя переменные, получим:

dy	=		x	dx ∫ctgy dy = ∫		x	dx .
		(x	2		(x	2
tgy			− 2)			− 2)

Второй интеграл найдем методом подстановки:

123

Индивидуальное задание и его решение

				x						x2 - 2 = t									1			dt	1										1									1
																																				2				2
																																										2
∫			2		dx =					2x dx = dt							=			∫			= ln			t	+ ln C = ln								x		- 2	+ ln C = ln	x		- 2			× C
	(x			- 2)						x dx =					1	dt			2			t	2										2
															2
Получим												общий								интеграл									исходного									уравнения:
														1
ln		sin y					x			2		- 2	2					,	где				C —					произвольная									положительная
					= ln										× C
постоянная.
Из полученного равенства выразим y :
							1																						1
sin y =					x2 - 2						× C										y = arcsin							x	2 - 2			× C				,	где C		—
									2																						2
												1																					1				1

произвольная постоянная.

3) Решить дифференциальное уравнение: y¢ = x + y . y - x

Разделим числитель и знаменатель дроби, стоящей в правой части

1 +

y

уравнения на x . Полученное уравнение имеет вид (4): y¢ =

x

.

y

-1

x

Для решения этого уравнения введем замену:

y

= z, y¢ = z¢x + z .

x

Получаем:

1 + z

1 + 2z − z 2

dz

z 2 − 2z −1

z¢x + z =

z′x =

= −

z -1

z −1

dx

(z −1)x

(z −1)dz

= −

dx

z 2 − 2z −

x

1

В полученном уравнении переменные разделены, поэтому можно брать интегралы от левой и правой частей:

∫		(z −1)dz			= −∫	dx
							.
	z	2	− 2z −1
						x

Вычислим первый интеграл:

124

Индивидуальное задание и его решение

(z −1)dz

(z −

1)dz

(z −1)2 − 2 = t

1

dt

1

1

∫

= ∫

=

2(z −1)dz = dt

=

∫

=

ln

t

+ C =

ln

(z −1)

2

− 2

+

z

2

− 2z −1

(z −1)

2

−

2

2

t

2

2

(z −1)dz =

1

dt

2

Имеем:

1

ln

(z −1)2 − 2

= −ln

x

+ C ln

(z −1)2 − 2

= −2ln

x

+ ln C

2

1

2 − 2

= ln(x

−2C )

(z −1)2 − 2

= x

−2C

ln

(z −1)

1

1

(z −1)

2 − 2 = ±C x−2

,

1

где C1 — произвольная положительная постоянная.

Последнее выражение можно записать одной формулой:

(z −1)2 − 2 = Cx −2 ,

где С — произвольная постоянная.

Таким образом, получаем: z =

Cx −2 + 2

+1.

Общее решение имеет вид: y = x(

+1).

Cx −2 + 2

4)

Решить

дифференциальное

уравнение:

xy′ − y = (x − y)

.

ln(x − y) − ln x

Преобразуем

данное уравнение: y′ −

y

= (1 −

y

)

ln(1 −

y

) — это

x

x

x

однородное д.у. первого порядка (см. (4)).

Как и в предыдущей задаче введем замену:

y

= z,

y

′

′

+ z .

x

= z x

Получаем:

(1 − z)

′

dz

ln(1 − z)

z x + z − z = (1 − z) ln(1 − z)

=

dx

x

dz

=

dx

(1 − z)

ln(1 − z)

x

∫

dz

= ∫

dx

.

(1 − z)

ln(1 − z)

x

125

Индивидуальное задание и его решение

Вычислим интеграл, стоящий в левой части равенства:

dz

ln(1 − z) = t

dt

∫

=

−

1

dz = dt

= −∫

= −2 t = −2

ln(1 − z) .

(1 − z)

ln(1 − z)

t

− z

1

Имеем:

− 2

= ln

x

+ ln C

= −

1

ln C

x

ln(1 − z)

ln(1 − z)

2

ln(1 − z) = ln 2 (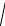C x ) z =1 − eln 2 C x ,

где C — произвольная положительная постоянная.

ln2

C

x

Получаем общее решение исходного д.у.: y = x 1

− e

.

5) Решить дифференциальное уравнение: xy′ = xe−

y

+ y .

x

Разделим обе части уравнения на

x . Исходное уравнение примет

вид (4):

y′ = e−

y

y

+

.

x

x

Введем следующую замену:

y

= z,

y

′

′

+ z .

x

= z x

Тогда получим:

′

−z

′

=

e−z

dz

=

e

−z

z

=

dx

z

= ∫

dx

z x + z = e

+ z z

e

dz

∫e

dz

x

dx

x

x

x

e z = ln

x

+ C z = ln(ln

x

+ C ).

Общее решение имеет вид: y = x ln(ln

x

+ C ).

6) Решить дифференциальное уравнение: y′cos x = −y sin x + 2x .

Преобразуем исходное д.у., разделив обе

его части на

cos x .

Получим

линейное

неоднородное

д.у.

1-го

порядка

(см.

(5)):

y′ + ytgx = 2x . cos x

126

Индивидуальное задание и его решение

Разобьем решение этого уравнения на несколько этапов.

a)

y = uv, y

′

′

′

′

′

+ uvtgx =

2x

= u v + uv

u v + uv

cos x

′

′

+ vtgx]=

2x

.

u v + u[v

cos x

б) v′ + vtgx = 0

dv

= −vtgx

dv

= −tgxdx

∫

dv

= −∫tgxdx

dx

v

v

ln

v

= ln

cos x

v = cos x .

Заметим, что при вычислении v знак модуля мы просто опустили,

так

как согласно общей методике достаточно иметь одну функцию v , обращающую в нуль квадратные скобки.

в) u′cos x =	2x	u′ =	2x			u = 2∫	x			dx .
	cos x		cos	2			cos	2
					x				x

К полученному интегралу применим формулу интегрирования по частям:

x

dv =

dx

u = x

dx =

cos2 x

= x tgx −

tgxdx = x tgx + ln

cos x

+ C .

∫cos2

∫

x

v = tgx

du = dx

Таким образом получаем: u = 2(x tgx + ln

cos x

+ C ).

г) Общее решение имеет вид: y = 2cos x(x tgx + ln

cos x

+ C) .

7) Решить дифференциальное уравнение: x2 y′ − 2xy = 2x5 y .

Приведем данное д.у. к виду (5): y′ −

2 y

= 2x3 y .

x

′

′

′

′

′

2uv

3

а)

y = uv, y

+ uv

−

= 2x

uv

= u v

u v + uv

x

′

′

2v

3

u v + u v

−

=

2x

uv .

x

б) v′ −

2v

= 0

dv

=

2v

dv

=

2dx

∫

dv

= 2∫

dx

ln

v

= 2ln

x

x

dx

x

v

x

v

x

127