14. Методические указания 2

Индивидуальное задание и его решение

ОБРАЗЕЦ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ ПО ЛИНЕЙНОЙ АЛГЕБРЕ

					Задача 1
	3 3		−5			4	1		2	2
Даны матрицы	A = 1	1	2		, B =	5	, C = 0		3	1	.
		−1	7					3	1	4
	2					7

1.Вычислить матрицу 4A+5C+7 CT .

2.Выполняется ли равенство AC=CA?

3.	Вычислить определители																				A	,		C		,		AC		,		CA		и проверить равенство:
		AC		=				CA		=		A		×		C		.
4.	Используя свойства определителей, вычислить определитель
						3			5				7				2
	=					1			2				3				4
						− 2				−3			3				2			.
						1			3				5				4
5.	Решить систему AX=B матричным методом.

Задача 2

1. Решить системы уравнений по формулам Крамера:

5x1 + 2x2					= 4					2x −3x					+ x = −7			x + 2x			+ 3x				=14
							,						1	2			3	1		2				3
										x1			+ 4x2 + 2x3 = −1, x1 + x2 + x3 = 6 .
7x1 + 4x2					= 8								x − 4x			2	= −5		x + x			2	= 3
													1						1
2. Решить систему уравнений методом Гаусса:
x1 −3x2 +5x3 −7x4 =12
	3x −5x			2	+ 7x				3	− x		4	= 0
	1												= 4 .
	5x −7x			2	+ x		3		−3x			4
	1
7x − x		2	+ 3x			3		−5x			4		=16
	1

Задача 3

Построить точки и векторы: A(1;−2), B(2;−8), AB ; C(1;0;2), D(3;−1;0), CD .

39

Индивидуальное задание и его решение

Задача 4

−1

3

Даны

векторы

a

=

, b

=

.

Вычислить

и

изобразить

в системе

2

4

координат следующие линейные комбинации векторов

и

b

:

a

+

,

b

2

+

,

−

a

b

b

a

a

2

Задача 5

−1

1

7

Найти

линейную комбинацию

векторов

2

,

3

,

5

с

a =

b =

0

c =

−3

−1

3

8

0

коэффициентами α = 3,

β = 4,

γ = −2 .

Задача 6

Будут ли векторы линейно зависимы или линейно независимы в случаях:

							− 4			−1
а)			2					; б)
	a	=		,	b =				a	= 1	,
			1				− 2			1

		− 2
b =		2	; в)
		1

			−1			− 2			2
		= 1 , b = 2 ,						=	−1 ?
	a						c
		1			1			3

Задача 7

			2				0				2
Даны три вектора		=	2	,	b =		1	,		=	1	. Доказать, что система {		, b ,				}
	a								c				a				c
		3				1				1

1

образует базис в R3 . Найти разложение вектора d = 0 по этому базису.

4

Задача 8

2

0

Даны два вектора

=

1

и

=

− 2

. Найти

, угол ϕ между векторами

b

a

a

a

0

1

и b , а также прb (2a −b ) .

40

Индивидуальное задание и его решение

Задача 9

			2					−1
При каком значении x вектор		=	− 6		ортогонален вектору b =			3	? При
	a
			x					4

			2					x
каких значениях x и y векторы c =			−6		и d =			y	параллельны?
			1
								−1

Задача 10

Вычислить площадь и высоту треугольника с вершинами A(7;3;4), B(1;0;6) и

C(4;5;7).

				Задача 11
Вершины треугольной пирамиды находятся в точках A1 (4;6;5) ,								A2 (6;9;4) ,
A3 (2;10;10) и	A4 (7;5;9) .	Вычислить:			а)	объем	пирамиды; б)	высоту,
опущенную из вершины A4
				Задача 12
Выяснить, лежат ли точки D(1;0;1), E(0;1;–3) в плоскости ABC, где A(5;–3;0),
B(–4;3;3), C(–4;2;4).
		РЕШЕНИЕ ЗАДАЧ
		Решение задачи 1.1
		1	0	3
	что CT =
Напомним,		2	3	1	—	матрица,	транспонированная к
			1
		2		4

матрице C (см. определение 3 из лекции 1), то есть такая, первый столбец которой совпадает с первой строкой матрицы C; второй столбец — со второй строкой, третий столбец — с третьей строкой. Чтобы умножить матрицу на число, нужно каждый элемент этой матрицы умножить на это число, а чтобы сложить матрицы одинаковых размеров, нужно сложить одноименные

41

																																Индивидуальное задание и его решение
элементы																этих										матриц										(см.							определение												7		из	лекции				3). Поэтому
																			12							12						- 20										5				10					10				7		0	21			24		22	11
4A+5C+7 CT																	=					4							4			8						+					0			15				5			+			14	21	7		=		18	40
																																																																20 .
																						8				- 4						28														5				20							7	28				37	8
																																										15													14									76
																																					Решение задачи 1.2
									Две матрицы можно перемножать, если число элементов в строке первой
матрицы равно числу элементов в столбце второй из перемножаемых матриц
(см. в лекции 3 определение 9 и диаграмму перед ним). Поэтому матрицы AC
и CA можно вычислить:
													3			3 - 5 1 2																		2						3 ×1 + 3 ×0 - 5 ×3															3 × 2 + 3 ×3 - 5 ×1 3 × 2 + 3 ×1 - 5 × 4
																																					=													+ 2 ×3						1× 2 +1×3 + 2 ×1 1×							2 +1×1 + 2 ×
	AC = 1															1			2 0 3															1						1×1 +1× 0																									4
															2	-1 7																										2	×1 -1× 0							+ 7 ×3						2 × 2 -1×3 + 7 ×1 2 ×							2 -1×1 + 7 ×		4
																										3 1								4
	-12														10		-11																																	9		3			13
=						7									7			11								и, аналогично, CA = 5																										2			13 . Значит, AC ¹ CA.
						23									8		31																																			6
																																																	18						15
																																					Решение задачи 1.3
									Используя формулу (4), а затем формулу (3) для вычисления
определителей третьего и второго порядка (см. лекцию 1), получаем:
				=								3			3		- 5				= 3 ×								1			2				- 3 ×					1		2				- 5 ×				1	1			= 3 ×9 - 3 ×3 - 5 × (-3) = 33 ;
	A											1 1					2
																													-1 7												2 7										2 -1
												2			-1		7
					=								1		2	2		= 1×							3 1						- 2			0 1					+ 2						0 3				= 1×11 - 2 ×(-3) + 2 × (-9) = -1;
	C												0 3 1
													3		1	4									1				4					3			4								3	1
									=						-12 10 -11														= -12 ×(217 - 88) -10 × (217 - 253) -11× (56 -161) = -33 ;
	AC														7		7					11
															23		8					31
							=								9	3	13						= 9(30 - 78) - 3(75 - 234) +13(30 - 36) = -33 .
	CA													5		2	13
														18		6	15

Теперь очевидно, что AC = A × C = CA . Иного и не могло быть в силу выполнения свойства 9 определителей (см. лекцию 2).

42

Индивидуальное задание и его решение

Решение задачи 1.4
Вычтем из элементов первой строки определителя	утроенные

элементы второй строки, прибавим к элементам третьей строки удвоенные элементы второй строки и, наконец, вычтем из элементов четвертой строки элементы второй строки. Согласно свойству 7 определителей (см. лекцию 2) величина определителя при этом не изменится, а сам определитель преобразуется к виду:

0	-1	- 2	-10
D = 1	2	3	4 .
0	1	9	10

0 1 2 0

Разложим этот определитель по элементам первого столбца, что возможно вследствие теоремы 1 (см. лекцию 3):

-1 - 2 -10

D = - 1 9 10 .

1 2 0

Прибавив к элементам второй и третьей строк элементы первой строки, получаем:

D = -		-1	- 2	-10		= -70.
		0	7	0
		0	0	-10

Решение задачи 1.5

Так как A ¹ 0 , то обратная матрица существует (теорема 3 из лекции 4). Чтобы найти A−1 , нужно найти все алгебраические дополнения aij* :

a	=	1 2						= 9; a			= -			1 2							= -3; a									=		1 1				= -3;
11		-1 7					12							2				7										13				2		-1
a21 = -						3	- 5			= -16; a22 =										3				- 5			= 31; a23							= -				3			3		= 9;
						-1	7													2				7														2 -1
a	=			3	- 5			=11; a				= -				3		- 5						= -11; a							33		=		3	3				= 0.
31				1	2			32								1		2																	1	1
По формуле (12) из лекции 4 имеем:																														9			-16			11
										A−1 =			1				× ( A )T							1
																								=					- 3 31											-11
													A
																								33					- 3					9		0

(проверить самостоятельно соотношение A−1 × A = I ).

43

Индивидуальное задание и его решение

Система уравнений AX = B имеет единственное решение X = A−1B (см. первую часть доказательства теоремы 4 из лекции 4). Таким образом:

x1x2 =x3

				9 -16		11				4						33				1
X =	1			- 3		-11		×				=	1					=
					31					5						66				2 .
	33												33
				- 3	9	0				7						33				1

Решение задачи 2.1

	2x1 - 3x2 + x3 = -7
Решим систему	x1 + 4x2 + 2x3 = -1					(остальные системы	решаются
		x	- 4x	2	= -5
		1
аналогично).
В соответствие	с правилом				Крамера	(см. теорему 4 из	лекции 4)

вычислим главный и вспомогательные определители данной системы:

D =		2		- 3		1		= 2 ×				4	2		+ 3 ×				1	2		+		1	4		= 16 - 6 - 8 = 2 ¹ 0;
		1		4		2
												- 4 0							1	0				1 - 4
		1		- 4		0
			− 7		−3		1										2			− 7			1						2	−3	− 7
1 =			−1			4 2				= −2;			2 =				1			−1			2		= 2;	3 =			1	4	−1		= −4.
			−5		− 4		0										1			−5 0									1	− 4	−5

В результате получаем:

x =	1	= − 2 = -1; x =		2	=	2	= 1; x =	3	= − 4 = -2.
	D			D				D
1		2	2		2		3		2

Решение задачи 2.2

Метод Гаусса — это приведение системы к треугольному виду с помощью элементарных преобразований, производимых над строками системы. Эти преобразования таковы: перестановка уравнений системы; умножение уравнений системы на число, неравное нулю; сложение уравнений системы. Практически удобнее приводить к треугольному виду не саму систему уравнений, а матрицу из коэффициентов при неизвестных и свободных членов. Переход от одной матрицы к другой будем записывать при помощи знака равносильности ~, а строки будем символически обозначать буквой С с индексами (например, выражение C2 − 3C1 означает,

что мы ко второй строке прибавили первую, умноженную на число –3) . Итак:

44

												Индивидуальное задание и его решение
1 - 3			5 - 7				12					- 3C		1 - 3				5		- 7				12								4
			7 -1					C										- 8 20						-				C			2
3 - 5							0			C	2		1	0 4											36							8 ~
	5 - 7		1 - 3				4					- 5C ~			0 8			- 24 32						-	56				C		3
											3		1																			4
								C			4	- 7C																C			4
	7 -1		3 - 5				16						1		0 20			- 32 44						-	68
1 -3			5 -7		12								1 - 3					5	- 7			12
			-2 5															- 2 5
0 1					-9 C3 -C2								0 1									- 9
0 1			-3 4		-7			C4 -5C2					~	0 0				-1 -1				2			C4 + 2C3 ~
0 5			-8 11		-17									0 0				2 -14				28
1 - 3			5 - 7						12							1		- 3 5 - 7									12
													1)C3
0 1			- 2 5						- 9 (-							0		1 - 2 5									- 9
	0 0		-1 -1						2				(-16)			~	0	0	1	1							- 2			.
											C4
	0 0		0 -16														0	0	0	1							- 2
									32

Таким образом, исходная система привелась к треугольному виду:

x1 - 3x2 + 5x3 - 7x4 = 12
	x2 - 2x3	+ 5x4 = -9
		.
	x3 + x4 = -2
	x4	= -2

Из последнего уравнения получаем x4 = -2 . Подставляя это значение в

предыдущее уравнение, получаем x3 = 0 . Подставляя	x4 = -2	и x3 = 0 во
второе уравнение, имеем: x2 = -9 - 5 × (-2) = 1. И,	наконец,	подставляя
x4 = -2 , x3 = 0 и x2 = 1 в первое уравнение, находим x1 = 1.

Решение задачи 3

Решить эту задачу самостоятельно, опираясь на заключительный раздел лекции 5.

																								Решение задачи 4
								Имеем:
													-1			3		1
2				a	+ b =2×										+		=			= OA;
														2		4		8
												-1			3	- 4
		a	– b =											-	=				= OB ;
												2			4	- 2
													-1			3				1
		a + b										1
										=			×		+			=					= OC.
2
												2 2				4				3

45

Индивидуальное задание и его решение

x2

8 A

3 C

− 4

0

1

x1

− 2

B

Решение задачи 5

							1		-1			7			3			- 4			-14			-15
						2		3			5			6			12				-10			8
3a + 4b - 2c = 3							-1	+ 4	0		- 2	- 3		=	- 3		+	0		+	6		=	3	.
																					0
							3		8			0			9			32						41

Решение задачи 6

а) Воспользуемся критерием линейной независимости двух векторов в

R2 (см формулу (15) из лекции 5). Для этого составим определитель второго порядка из столбцов координат данных векторов:

D = D(a , b ) = 2 - 4 = -4 + 4 = 0 . 1 - 2

Следовательно, векторы a и b линейно зависимы.

б) Проверим, пропорциональны ли соответствующие координаты

векторов a и b : −1 = 1 ¹ 1 . Не пропорциональны! Следовательно, ни один из

- 2 2 1

векторов a и b не может быть выражен через другой. По свойству 1 систем векторов (см. лекцию 5) данные векторы линейно независимы.

в) Согласно критерию линейной независимости трех векторов в R3 (опять см формулу (15) из лекции 5) составим определитель третьего порядка:

46

Индивидуальное задание и его решение

								-1	- 2	2			2	-1		1	-1		1	2
D = D(						)=
		,		,				1	2	-1		= -1			+ 2			+ 2			=
			b
	a				c
								1	1	3			-1	3		1	3		1	1

= -(6 +1) + 2(3 +1) + 2(1 - 2) == -7 + 8 - 2 = -1 ¹ 0.

Следовательно, векторы a, b, c линейно независимы.

Решение задачи 7

													2		0	2
			Вычислим D(			,		,		) =			2		1	1			= 2(1 -1) + 2(2 - 3) = -2 ¹ 0 . Таким образом,
					a		b		c
													3		1	1
данная система векторов образует базис вR3 (см свойство 6 систем векторов
из лекции 5). Следовательно,																	= x1				+ x2		+ x3		. Найдем коэффициенты x1 ,
																d				a		b		c
													1
x		,	x	разложения								=		0			по			этому базису. Для этого перепишем
	2										d
			3
														4

предыдущее равенство в координатной форме

	1			2			0			2
		= x1			+ x2			+ x3
	0			2			1			1 ,
	4			3			1			1
откуда получаем систему:
		2x1 +			2x3 = 1
		2x1 + x2 + x3 = 0 .
		3x1 + x2 + x3 = 4

Решим эту систему по формулам Крамера:

x =	1	=	−8	= 4; x =	2	= -	9	; x =	3	= -	7	.
	D		- 2		D				D
1				2		2		3		2

В результате получаем нужное разложение d = 4a - 9 b - 7 c. 2 2

Решение задачи 8

Используя определения нормы и угла между векторами (см. определение 18 из лекции 6), находим:

a = 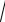22 +12 + 02 = 5 ; b = 0 + (-2)2 +12 = 5 ;

47