
- •Часть 3. Динамика Введение в динамику
- •Глава 1. Динамика мт
- •1.1. Законы (аксиомы) динамики мт Закон инерции
- •Основной закон динамики
- •Закон равенства действия и противодействия
- •Закон независимости действия сил
- •Системы основных единиц
- •1.2. Дифференциальные уравнения движения свободной и несвободной мт
- •1.3. Две основные задачи динамики мт
- •1.3.1. Первая (прямая) задача динамики мт
- •1.3.2. Вторая (обратная) задача динамики мт
- •1.4. Алгоритм решения первой и второй задач динамики мт – схема алгоритма д14 озд с комментариями и примерами
- •Комментарии
- •Пример 1
- •1.5. Колебательное движение мт
- •1.5.1. Уравнение колебательного движения мт
- •1.5.2. Колебательное движение мт в среде без сопротивления при отсутствии возмущающей силы
- •1.5.3. Колебательное движение мт в среде с сопротивлением при отсутствии возмущающей силы
- •1.5.4. Колебательное движение мт в среде без
- •1.5.6. Колебательное движение мт в поле силы тяжести, в среде с сопротивлением под действием возмущающей силы
- •1.6. Общие теоремы динамики мт
- •1.6.1. Теорема об изменении количества движения мт
- •1.6.2. Теорема об изменении момента количества движения мт
- •1.6.3. Теорема об изменении кинетической энергии мт, работа силы
- •1.7. Принцип Даламбера для мт
1.5.2. Колебательное движение мт в среде без сопротивления при отсутствии возмущающей силы
В этом случае n=0, h=0 и общее решение (1.23) примет вид:
![]() ,
(1.24)
,
(1.24)
где а и – постоянные интегрирования, которые находятся из начальных условий.
МТ перемещается по закону синуса (или косинуса). Такое движение носит название простого гармонического колебания, график его представлен на рис. 6.
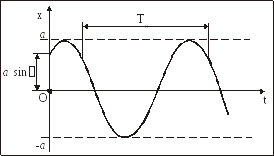
Рис. 6
Скорость этого гармонического колебания МТ будет:
![]() .
(1.25)
.
(1.25)
Так
как ![]() ,
то постоянная а
определяет наибольшее отклонение МТ
от центра колебаний О и называется
амплитудой колебаний МТ. Параметр
,
то постоянная а
определяет наибольшее отклонение МТ
от центра колебаний О и называется
амплитудой колебаний МТ. Параметр
![]() определяет положение МТ и ее скорость
в каждый момент времени и называется
фазой колебаний, а постоянная α –
начальной фазой.
определяет положение МТ и ее скорость
в каждый момент времени и называется
фазой колебаний, а постоянная α –
начальной фазой.
На
основании уравнения (1.24) можно сделать
вывод, что движение МТ является
периодическим. Периодом колебаний
называется промежуток времени Тп,
в течение которого МТ совершает одно
полное колебание, т.е. МТ в момент времени
t
+ Tп
должна прийти в то же положение х и иметь
ту же скорость
![]() ,
что и в момент времениt:
,
что и в момент времениt:
![]() ,
,
![]() .
.
Наименьшее
значение t,
при котором выполняются эти условия,
определяются равенством
![]() ,
откуда
,
откуда
![]() .
.
Величина обратная периоду, определяет число колебаний, совершаемых МТ за одну секунду, и ее называют частотой колебаний:
![]() .
.
Соответственно параметр ω называется круговой частотой колебаний. Необходимо отметить, что частота и период колебаний МТ от начальных условий не зависят.
1.5.3. Колебательное движение мт в среде с сопротивлением при отсутствии возмущающей силы
В этом случае h = 0 и решение может быть представлено формулами (1.18) – (1.20),так как х=х
При малом сопротивлении среды (n < ) в соответствии с формулой (1.18) ;
![]() ,
(1.26)
,
(1.26)
где а и – постоянные интегрирования, которые находятся из начальных условий.
Из
уравнения (1.26) следует, что движение МТ
будет колебательным. Эти колебания
называют затухающими, так как за счет
множителя
![]() размахи колебаний будут убывать, стремясь
с течением времени к нулю. Период
затухающих колебаний
размахи колебаний будут убывать, стремясь
с течением времени к нулю. Период
затухающих колебаний
![]() .
.
Графически затухающие колебания можно иллюстрировать затухающей синусоидой (рис. 7).
Чтобы
установить закон затухания размахов
колебания, отметим, что промежуток
времени между двумя последовательными
максимальными отклонениями МТ
![]() и
и![]() равен периоду Тп,
т.е.
равен периоду Тп,
т.е.
![]() .
С учетом этого найдем:
.
С учетом этого найдем:
![]() .
.
Отсюда
следует, что наибольшие отклонения МТ
убывают с течением времени по закону
геометрической прогрессии, знаменатель
которой
![]() называется декрементом колебаний.
Соответственно величина
называется декрементом колебаний.
Соответственно величина![]() называется логарифмическим декрементом
затухания.
называется логарифмическим декрементом
затухания.
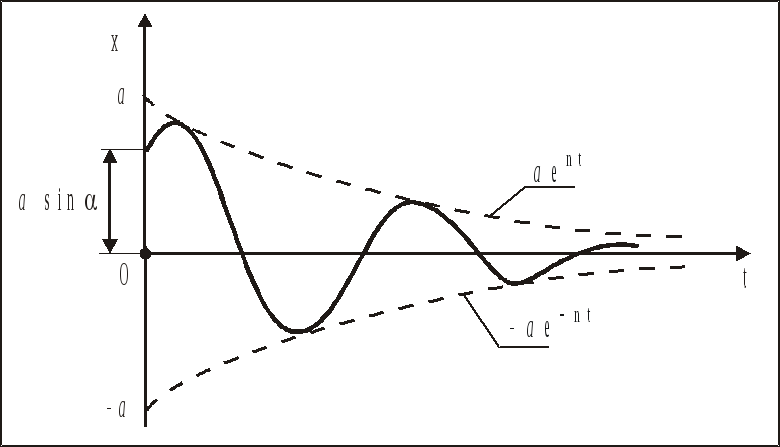
Рис. 7
В случае большого сопротивления среды (n > ) движение МТ будет неколебательным (апериодическим) затухающим – формула (1.19):
![]() ,
,
где
![]() – действительные отрицательные числа,
а С1 и
С2
- постоянные интегрирования, которые
находятся из начальных условий.
– действительные отрицательные числа,
а С1 и
С2
- постоянные интегрирования, которые
находятся из начальных условий.
График
этого движения МТ в зависимости от
величины и знака начального отклонения
х0
и направления начальной скорости
![]() имеет форму одной из кривых, изображенных
на рис. 8 (или им симметричных относительно
оси абсцисс).
имеет форму одной из кривых, изображенных
на рис. 8 (или им симметричных относительно
оси абсцисс).
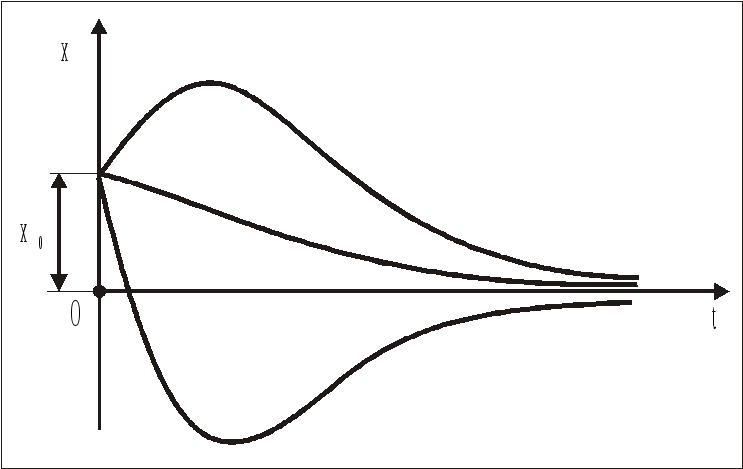
Рис. 8
В предельном случае (n = ) движение МТ также будет неколебательным (апериодическим) затухающим – формула (1.21):
![]() ,
,
где С1 и С2 – постоянные интегрирования, которые находятся из начальных условий.
Картина движения МТ будет качественно такой же, как показанная на рис. 8.
