Математика Шумаев В В

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

5)( ) = ( ) – ассоциативность a a

6)(+) = + - дистрибутивность a a a

7)( a + b ) = a + b

8) 1 = a a

Длина вектора в координатах определяется как расстояние между точками начала А(х1, y1, z1)и конца вектора B(x2, y2, z2):

AB (x2 x1)2 ( y2 y1)2 (z2 z1)2 .

Если точка М(х, у, z) делит отрезок АВ в соотношении , то ко-

ординаты этой точки определяются как:

x

x1 x2

;

y

y1 y2

;

z

z1 z2

.

1

1

1

В частном случае координаты середины отрезка находятся как:

x = (x1 + x2)/2;

y = (y1 + y2)/2;

z = (z1 + z2)/2.

3.2 Скалярное произведение векторов

Скалярным произведением векторов

и

a

b называется число,

равное произведению длин этих сторон на косинус угла между ними.

cos

a

b = a b

Свойства скалярного произведения

1)

2

;

a

a

= a

2)

a

b

= 0, если a

b

или a = 0 или b = 0.

3)

;

a

b

= b a

4)

+ c ) =

a

(b

a

b + a c ;

5) (m a ) b = a (mb ) = m( a

b );

Если рассматривать векторы a(xa , ya , za );

b(xb , yb , zb ) в декар-

товой прямоугольной системе координат, то

a

b = xa xb + ya yb + za zb;

Угол между векторами:

cos

xa xb ya yb za zb

;

a

b

3.3 Векторное произведение векторов

Векторным произведением векторов

,

a и b

называется вектор c

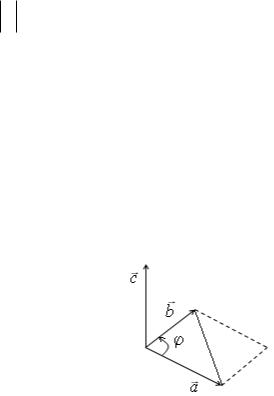
удовлетворяющий следующим условиям:

20

1)

-

угол между векторами

и

c

a

b sin , где

a

b ,

sin 0;	0
2) вектор c			ортогонален векторам a	и b
			образуют правую тройку векторов (правой тройкой
3) a	, b	и c
векторов a ,		b и	c называется система трёх векторов, если поворот
вектора a совмещающий его по кратчайшему пути с вектором b , со-

вершается против часовой стрелки для наблюдателя, глаз которого
помещается на конце вектора c ).
Обозначается: c	a	b	или c	[a, b].

Рисунок 6 – Схема векторного произведения векторов

Свойства векторного произведения векторов

1) b

a

a

b ;

0 ,

2) a

b

a

b ;

3) (m a ) b =

a (mb ) = m( a

b );

4) a

( b

+ с ) = a

b +

a

с ;

5) Если заданы векторы a

(xa, ya, za) и b (xb, yb, zb) в декартовой прямо-

угольной системе координат с единичными векторами i ,

j, k

, то

i

j

k

xa

ya

za

a

b =

xb

yb

zb

6) Геометрическим смыслом векторного произведения векторов явля-
ется площадь параллелограмма, построенного на векторах a и b .
3.4 Смешанное произведение векторов
Смешанным произведением векторов a		, b	и c называется чис-
ло, равное скалярному произведению вектора
			a на вектор, равный
векторному произведению векторов b	и c . Обозначается a			b	c .
21

Смешанное произведение a

b

c по модулю равно объему па-

раллелепипеда, построенного на векторах a , b

и c .

Свойства смешанного произведения.

1)Смешанное произведение равно нулю, если: хоть один из векто-

ров равен нулю; два из векторов коллинеарны; векторы компланарны.

2)

(a

b) c

a

(b

c)

3)

(a

b c) (b

c a) (c

a

b )

(b

a c) (c

b

a) (a

c

b )

4) ( a1

a2

b c) (a1

b c)

(a2

b

c)

,

5) Объем треугольной пирамиды, образованной векторами a

b

, равен

и c

6)Если 1 1 1 , a (x , y , z )

a

6 a b c b (x2 , y2 , z2 ),

			x1	y1
			x2	y2
b	c
			x3	y3

c (x3, y3, z3) , то z1

z2 z3

Рисунок 5 – Схема смешанного произведения векторов

Контрольные вопросы.

1.Что такое вектор, как находятся его координаты и длина, если даны координаты начала и конца?

2.Что такое скалярное произведение векторов?

3.Что такое векторное произведение векторов и как оно записы-

вается?

4.Что такое смешенное произведение векторов и как оно записывается?

5.Перечислите геометрические смыслы произведений векторов.

22

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

4 АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ

Любое уравнение, связывающее координаты x, y, z любой точки поверхности является уравнение поверхности в пространстве.

Плоскостью называется поверхность, все точки которой удовле-

творяют общему уравнению плоскости:

Ax + By + Cz + D = 0,

где А, В, С – координаты вектора N Ai	Bj	Ck - вектор нормали

к плоскости.

Уравнение плоскости, проходящей через три точки:

x x1	y y1	z z1
x2 x1	y2 y1	z2 z1	0
x3 x1	y3 y1	z3 z1

Уравнение плоскости по точке и вектору нормали:

A(x x0 ) B( y y0 ) C(z z0 ) 0

Уравнение плоскости в отрезках:

ax by cz 1

Каждое из чисел a, b, c являются координатой точки пересечения плоскости соответственно с осями х, у, z.

Расстояние от точки М0(х0, у0, z0) до плоскости

Ах+Ву+Сz+D=0 равно:

d		Ax0	By0 Cz0	D			.
			A2 B2 C 2

Уравнение линии в пространстве. В пространстве любая линия может быть определена как совокупность точек, координаты которых в некоторой выбранной в пространстве системе координат удовле-

творяют уравнению линии в пространстве: F(x, y, z) = 0.

Линия в пространстве можно рассматривать как линию пересечения двух поверхностей, каждая из которых задана каким-либо уравнением. Пусть F(x, y, z) = 0 и Ф(x, y, z) = 0 – уравнения поверхностей, пересекающихся по линии L. Тогда пару уравнений

F (x, y, z) 0Ф(x, y, z) 0

23

назовем уравнением линии в пространстве.

Направляющим вектором прямой называется всякий (нулевой)

вектор, лежащий на прямой (или параллельный ей).

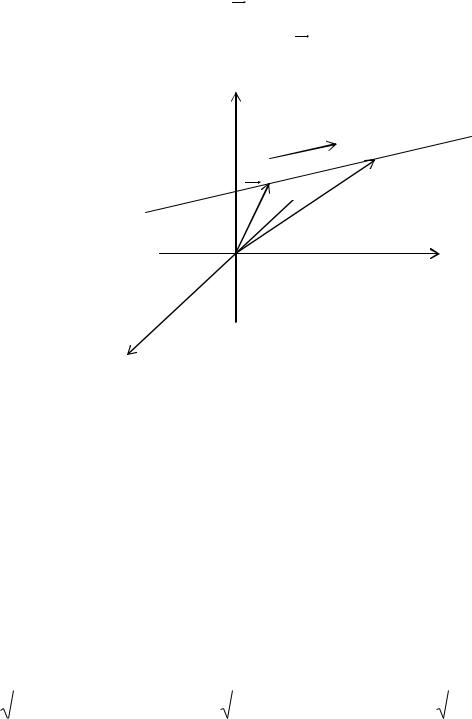
Уравнение прямой в пространстве по точке и направляющему вектору.

		= r0
	r		+ S t.
где S	- направляющий вектор прямой; r0 , r -радиус- векторы произ-

вольных точек М0(x0, y0, z0) и M(x, y, z); t – некоторый параметр. z

S M1

M0

r0 r

0

y

x

Рисунок 6 - Прямая в пространстве

Параметрические уравнения прямой:

x x0 mt

y y0 ntz z0 pt

Канонические уравнения прямой в пространстве:

x x0		y y0		z z0	.
m		n		p

Углы α, β, γ, образуемые прямой с осями координат, находятся из соотношений:

cos		m		; cos		n		; cos		p
		m2 n2 p 2				m2 n2 p2				m2 n2 p2

m : n : p = cos : cos : cos .

Числа m, n, p называются направляющими коэффициентами прямой, а cos , cos , cos - направляющие косинусы прямой.

24

В случае если m, n или p равняются нулю в уравнениях прямой следует приравнять нулю соответствующие числители.

Уравнения прямой в пространстве, проходящей через две точки

M1(x1, y1, z1) и M2(x2, y2, z2):

x x1			y y1				z z1			.
x	x		y	2	y		z	2	z
2	1				1				1

Общие уравнения прямой:

A1x B1 y C1z D1 0A2 x B2 y C2 z D2 0

Направляющий вектор прямой может быть найден как вектор-

ное произведение векторов нормали к заданным плоскостям:

	N1	N2			i
S					A1
					A2

i m jn kp.

j

k

B

C

A

C

A

B

B C

i

1

1

j

1

1

k

1

1

1

1

B2

C2

A2

C2

A2

B2

B2

C2

Угол между плоскостями в пространстве.

Рисунок 7 - Угол между плоскостями Угол между векторами нормали:

cos

N1

N2

.

1

N1

N2

Угол между плоскостями:

cos

A1 A2 B1B2 C1C2

A2

B2

C 2

A2

B2

C 2

1

1

1

2

2

2

25

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Условия параллельности и перпендикулярности плоскостей. Для того, чтобы плоскости были перпендикулярны необходимо и

достаточно, чтобы косинус угла между плоскостями равнялся нулю.

A1 A2 B1B2 C1C2 0 .

Плоскости параллельны,

векторы

нормалей

коллинеарны:

N

N

.Это условие выполняется, если:

A1

B1

C1

.

2

1

A2

B2

C2

Угол между прямыми в пространстве.

cos

S1

S2

m1m2 n1n2 p1 p2

.

S1

S2

m12 n12 p12

m22 n22 p22

Условия параллельности и перпендикулярности прямых в про-

странстве.

Чтобы две прямые были параллельны необходимо и достаточно,

чтобы направляющие векторы этих прямых были коллинеарны:

m1

n1

p1

m2

n2

p2

Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю.

m1m2 n1n2 p1 p2 0

Углом между прямой и плоскостью называется любой угол ме-

жду прямой и ее проекцией на эту плоскость.

Рисунок 8 - Угол между прямой и плоскостью

26

Этот угол может быть найден по формуле: sin cos

N

S

N

S

В координатной форме: sin

Am Bn Cp

A2 B2 C 2

m2 n2 p

2

Условия параллельности и перпендикулярности прямой и плоскости в пространстве.

Для того, чтобы прямая и плоскость были параллельны, необхо-

димо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были перпендикулярны. Для этого необходимо,

чтобы их скалярное произведение было равно нулю.
			0,	sin 0,	Am Bn Cp 0.
N S,		N S

Для того, чтобы прямая и плоскость были перпендикулярны, не-

обходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были коллинеарны. Это условие выполняется, если векторное произведение этих векторов было равно нулю.

N S 0;		A	B		C
		m		n		p

Пример 4.1. Заданы координаты четырех вершин пирамиды

ABCD. А(-2,0,0), B(1,1,-1), С(-1,3,0), D(-1,0,2). Найти: 1) длину АВ; 2)

угол φ между векторами АВ и АС;3) площадь грани AВС; 4) объем пирамиды; 5) длину высоты DH пирамиды, проведенной к плоскости грани АВС. Записать уравнения: 6) прямой АВ; 7) плоскости АВС; 8) высоты пирамиды DH; 9) высоты АК треугольника АВС,

Решение. 1. Вектор AB имеет длину равна:

AB

(x

2

x )2 ( y

2

y )2

(z

2

z )2

1

1

1

(1 2)2

(1 0)2

( 1 0)2

11

Координаты вектора AB определяются

AB (x2

x1)i

( y2 y1) j (z2 z1)k ,

AB (3;1;-1)

2. Угол φ между векторами AB и AC

определяется по формуле

cos

ab

| a || b |

Найдём длину вектора AC : AÑ ( 1 2 )2 ( 3 0 )2 ( 0 0 )2 10

27

Координаты вектора AC – (1;3;0)
Скалярное произведение вычислялось по формуле
a	b = xa xb + ya yb + za zb =3·1+1·3+1·0=3+3+0=6
			cos							AB BC									3									3			0							6
							| AB || BC |														11									10								110
						arccos(												6										) 55
																				110
3. Площадь треугольника АВС
								SΔABC =1/2 | AB AC |.
Вычислим координаты векторов															AB и													AC векторное произведение
AB AC .
												i	j				k
				AB AC												1
												3 1																3i			1 j							8k ;
												1	3	0
										1																			1
			S ABC									32 12 82																		74( åä2 )
									2
																										2
4. Объем пирамиды ABCD
						1			x1			y1		z1							1					3				1					1
V		a	b	c					x2			y2		z2												1				3					0						2.5 êâ.åä
						6															6
									x3			y3		z3												1 0 2

5. Длина высоты DH пирамиды, проведенной из вершины D к грани АВС

DH =	3V			3 2.5					15
	S ABC			1
							74
					74
				2

6. Уравнение прямой АВ будем искать по двум заданным точкам этой прямой А и В.

x xA		y yA		z zA
xB xA		yB yA		zB zA

Подставляя в последнее уравнение координаты точек А и В, получим

(x+2)/3=y=-z

7. Уравнение плоскости АВС можно записать по координатам тpёх точек А,В,С в виде

28

x xA		y yA		z zA
xB xA		yB yA		zB zA			0
xC xA		yC yA		zC zA
x 2
	y	z			1	1			3	1		3	1
3	1	1	(x 2)					y			z
1	3	0			3	0			1	0		1	3

3(x 2) y 8z 3x y 8z 6

Уравнение плоскости АВС: 3x- y+8z+6 =0

8. Уравнение высоты DH пирамиды ищем в виде

x xD y yD z zD
m	n	p

Координаты точки D известны, а направляющий вектор прямой

a (т,п,р) коллинеарен вектору нормали к плоскости АВС и имеет координаты N (3,-1,8). Поэтому уравнение прямой DH имеет вид

x xA

y yA

z zA

m

n

p

x 1

y

z 2

1

3

8

9. Уравнение высоты АК. Направляющий вектор прямой АК,

вектор

N

(3,-1,8)-нормали к

a (m,n,p) перпендикулярен вектору

может быть вычислен

плоскости АВС и вектору ÂC (-2,2,1). Вектор a

i

j

k

a

N ÂC

3

1

8

17i

19 j 4k

2

2

1

x 2

y

z

Уравнениевысоты АК имеет вид

19

17

4

Контрольные вопросы.

1.Что называют уравнением линии в пространстве?

2.Каково параметрическое уравнение линии в пространстве?

3.Каковы условия параллельности и перпендикулярности плоскостей, прямой и плоскости?

4.Как найти угол между двумя прямыми и плоскостями в пространстве?

5.Какими способами может быть задана прямая в пространстве?

29