Математика Шумаев В В

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

интегралов переносятся и на задачу вычисления определенных интегралов.

8.3.2 .Замена переменных в определенном интеграле

b

Пусть задан интеграл f (x)dx , где f(x) – непрерывная функция

a

на отрезке [a, b]. Введем новую переменную в соответствии с форму-

лой x = (t).

Тогда если

1)( ) = а, ( ) = b

2)(t) и (t) непрерывны на отрезке [ , ]

3)f( (t)) определена на отрезке [ , ], то

									b
									f (x)dx f [ (t)] (t)dt
									a
				Тогда
	f [ (t)] (t)dt F[ (t)]												F[ ( )] F[ ( )] F (b) F (a)
																											1
																												1 x2 dx
				Пример 8.1. Вычислить определённый интеграл
																											0
				Решение.
1						x sin t;										/ 2										/ 2		cos2 tdt
		1 x2 dx														1				sin 2 t cos tdt
0						0;						/ 2				0											0
	1			/ 2				1				1						/ 2					1
				0	(1 cos 2t)dt				t					sin 2t											sin		.
	2							2				2						0			4 4					4

При замене переменной в определенном интеграле следует помнить о том, что вводимая функция (в рассмотренном примере это функция sin) должна быть непрерывна на отрезке интегрирования.

8.3.3 Интегрирование по частям

Если функции u(x), v(x) непрерывны вместе со своими производными на [a,b], то

b			b
u dv= uv		ba	- v du
a			a
60

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

												2
		Пример 8.2. Вычислить интеграл x ex dx
												0
		Решение.
	2		u x,				dv exdx				2	2
	x ex dx									xex		ex dx
			du			dx,		v e	x		0
	0											0
					2 2e2 e2 1 e2 1.
	2e2 0 ex
					0

8.4 Приложения определенных интегралов

Вычисление площадей плоских фигур Если криволинейная трапеция ограничена осью Ох, прямыми

х=а, х=b (a<b) и непрерывной кривой y=f(x), то ее площадь

b

S f (x)dx если f (x) 0 на [a;b] или

	a
		b
	S	f (x)dx		если f (x) 0 на [a;b].
		a
Если	криволинейная			трапеция ограничена кривыми
y f1(x),	y f2 (x),	f1(x)		f2 (x) и прямыми х=а, х=b

b

S f1 (x) f2 (x) dx .

a

Вычисление объемов тел вращения Объем тела, полученного от вращения вокруг оси Ох фигуры,

ограниченной непрерывной кривой y=f(x), прямыми х=а, х=b и осью абсцисс, вычисляется по формуле

b

Vx y 2 dx .

a

Объем тела, полученного от вращения вокруг оси Оу фигуры, ограниченной непрерывной кривой х= (у), прямыми у=с, у=d и осью

d

ординат, вычисляется по формуле Vу x2 dy .

с

Пример 8.3. Найти площадь фигуры, ограниченной линиями y = x, y = x2, x = 2.

Решение. Начертим схему.

61

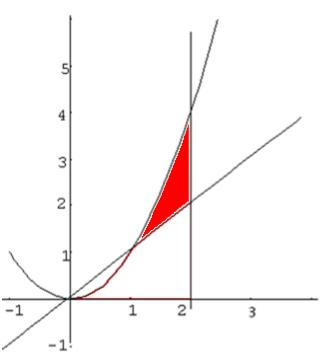
Рисунок 15 – Схема площади фигуры ограниченной линиями y =x, y = x2, x = 2

Искомая площадь (заштрихована на рисунке) может быть найдена по формуле:

			2			2	x3			x2			2			8						4				1				1		5
	S x2 dx xdx																																(ед2)
			1			1		3		2			1			3 2 3 2 6
Пример 8.4. Найти объем тела, образованного вращением фигу-
ры y 2	16	,		x 1, x 6 вокруг оси Ох.
	x2
Решение.						По формуле (1),				учитывая,													что a 1, b 6,											y 2	16
																																			x2
получим
6			16				6							1					6				40
Vx						dx 16 x 2dx 16																				(куб. ед.).
					2																				3
1				x			1							x					1
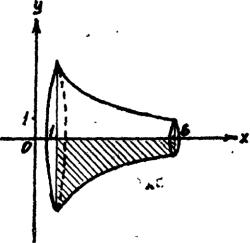
Пример 8.5. Вычислить объем тела,																					образованного вращением

вокруг оси Оу фигуры, ограниченной параболой x2 4 y и прямыми y 1, y 4, x 0 .

Решение. Учитывая, что c 1, d 4, x2 4 y , получим

62

4	y2				4
Vy 4 ydy 4						2 (16 1) 30 (куб. ед.).
		2
1					1

Рисунок 16 – Схема к определению объёма тела

Контрольные вопросы.

1.Дайте определение определённого интеграла.

2.Сформулируйте теорему НьютонаЛейбница.

3.Перечислите методы интегрирования определённого интеграла.

4.Перечислите свойства определённого интеграла.

5.Запишите формулу для нахождения площади поверхности вращения.

6.Запишите формулу для нахождения площади криволинейной трапеции.

7.Запишите формулу для нахождения площади криволинейного сектора.

8.Запишите формулу для нахождения объема тела вращения.

9.Напишите формулу интегрирования по частям в определённом интеграле.

10.Каково геометрическое приложение определённого интеграла.

63

9 НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

b

Если существует конечный предел lim f (x)dx , то этот предел

b a

называется несобственным интегралом от функции f(x) на полуинтервале [a, ).

	b
Обозначение: lim	f (x)dx f (x)dx
b a		a

Таблица 4 - Виды несобственных интегралов и их предельный переход

			Вид интеграла	Дополнительная		Предельный пе-
					операция	реход
			b				b
рода			f (x)dx			lim	f (x)dx
						a a
первого							b
			f (x)dx			lim	f (x)dx
			a			b a
Интегралы				c			с
						+ lim			f (x)dx
				f (x)dx f (x)dx		lim		f (x)dx +
						a	a
			f (x)dx		c
								b
				с – произвольная
					точка	b с
	b
	f (x)dx					lim	b
	a						f (x)dx
рода	а – точка разрыва функ-					e 0 a e
	ции		f (x)
второго
	b					lim	f (x)dx
	f (x)dx
						b e
	a
Интегралы	b – точка разрыва функ-			с	b	e 0	a
			f (x)			e 0
	ции
	b					c e
		f (x)dx				lim		f (x)dx +
	a			f (x)dx f (x)dx		a
	с (а<с<b)– точка разрыва						b
				a	с
	функции f (x)					+ lim			f (x)dx
						e 0
							c e
				64

Несобственным интегралом первого рода функции f (x) на промежутке [a, ) называют предел

		b
f (x) dx	lim	f (x) dx .
a	b a

Если этот предел существует и конечен, то несобственный интеграл называют сходящимся, в противном случае – расходящимся.

Несобственным интегралом второго рода функции f (x) на промежутке [a,b] называют предел (а – точко разрыва функции f (x) )

b		b
f ( x )dx lim		f ( x )dx .
a	e 0	a e

Если этот предел существует и конечен, то несобственный интеграл называют сходящимся, в противном случае – расходящимся.

Пример 9.1. Вычислить cos xdx

0

Решение.

b

b

cos xdx lim

cos xdx lim

sin x

lim (sin b sin 0) lim sin b

- не

0

b

0

b

0

b

b

существует. Несобственный интеграл расходится.

1

dx

Пример 9.2. Вычислить

x2

Решение.

1

dx

1dx

1

1

1

lim

lim

lim

1

1

- несобственный ин-

2

2

x

b b x

b

x

b

b

b

теграл сходится.

Контрольные вопросы.

1.Что называется несобственным интегралом?

2.Дайте определение несобственного интеграла первого рода.

3.Дайте определение несобственного интеграла второго рода.

4.Что такое сходящийся и расходящийся несобственный интеграл.

5.Какой несобственный интеграл называют абсолютно сходя-

щимся?

6.Напишите формулу интегрирования по частям.

7.Перечислите виды предельных переходов.

65

ЗАДАНИЕ К РАСЧЁТНО-ГРАФИЧЕСКОЙ РАБОТЕ №1

1.В задачах решить систему уравнений:

1)по формулам Крамера;

2)методом Гаусса;

3)матричным методом.

1.	2x 3y z 6			2.	4x 2 y z 1
	x 2 y z 5				3x y z 1
			6 y 3z 1
	x				x 4 y 5z 8
3.	2x y z 10			4.	5x 2 y z 10
						3y 2z	7
	3x 2 y z 14				4x
	x 3y 2z 6				x 6 y 5z 2
5.	2x 2 y 5z 12			6.	x 2 y z 5
			3y 7z 2				0
	x				3x 4 y 2z
	x 5 y z 6				2x 5 y z 7
7.	x 3y 6			8.	4x y 3z 5
	3x 5y z 3				x 2 y 4z 0
	2x y 3z 11				3x 3y 5z 11
9.		x 3y z 2		10.	5x 4 y z 5
	5x 2z 18				3x 6 y 2z 5
							21
	3x y 6z 7				2x 3y 4z
11.	x y z 1			12.	x y z 0
			2 y z 2			3y 4z	0
	x				2x
			y 2z 0			11y 10z 0
	x				4x
13.	2x 2 y 3z 0			14.	x y 2z 9
			2 y z 6			3y 2z	4
	x				4x
	x 4 y 4z 6				9x 2 y 4z 5
15.	2x 5 y 4z 8			16.	2x 2 y 5z 12
	3x 15 y 9z 5				x 3y 7z 2
	5x 5 y 7z 27				x 5 y z 6
				66

17.x 3y z 52x y 3z 53x y z 5

19.2x 3y z 0x y 2z 3

3x 2 y 3z 3

21.2x 3y z 0x y 2z 3x 2 y z 3

23.2x 3y 2z 3x 2 y z 1

2x y z 2

25.x 2 y z 1x 3y 2z 0x 4 y 3z 7

18. x 3y 63x 5y z 3

2x y 3z 11 20. x 3y z 2

5x 2z 18

3x y 6z 7

22.4x 2 y z 13x y z 1x 4 y 5z 8

24.5x 2 y z 104x 3y 2z 7

x 6 y 5z 2

2. В задачах даны координаты вершины треугольника АВС (таб-

лица 5): А(х1;у1); В(х2;у2); С(х3;у3). Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внут-

ренний угол А в радианах с точностью до 0,01; 4) уравнение высоты СD и ее длину; 5) уравнение окружности, для которой высота СD есть диаметр.

Таблица 5 – Данные к заданию 2.

№ зада-	А	В	С		№ зада-	А	В	С
ния					ния
1	(1;-6)	(3;4)	(-3;3)		14	(0;2)	(-7;-4)	(3;2)
2	(-4;2)	(8;-6)	(2;6)		15	(7;0)	(1;4)	(-8;-4)
3	(-5;2)	(0;-4)	(5;7)		16	(1;-3)	(0;7)	(-2;4)
4	(4;-4)	(6;2)	(-1;8)		17	(-5;1)	(8;-2)	(1;4)
5	(-3;8)	(-6;2)	(0;-5)		18	(2;5)	(-3;1)	(0;4)
6	(-2;-3)	(1;6)	(6;1)		19	(-1;-4)	(9;6)	(-5;4)
7	(-4;2)	(-6;6)	(6;2)		20	(10;-2)	(4;-5)	(-3;1)
				67

Продолжение таблицы 5

8	(4;-3)	(7;3)	(1;10)	21	(1;2)	(-7;4)	(-1;2)
9	(4;-4)	(8;2)	(3;8)	22	(7;3)	(5;4)	(-1;-5)
10	(-3;-3)	(5;-7)	(7;7)	23	(-1;-2)	(4;7)	(-2;3)
11	(-3;-1)	(-4;-5)	(8;1)	24	(-2;2)	(4;-2)	(2;5)
12	(-2;-6)	(-3;5)	(4;0)	25	(1;4)	(-8;3)	(1;2)
13	(-7;-2)	(3;-8)	(-4;6)

3. Определить вид кривой второго порядка и построить её (таблица 3).

1.x2 y2 10x 5y 951 0

2.4x2 25y2 16x 125y 234 0

3.9x2 27x 6 y 54 0

4.36y2 4x 72y 98 0

5.16x2 4y2 64x 40y 124 0

6.25x2 9y2 75x 180y 149 0

7.36x2 25y2 72x 400y 452 0

8.4 y2 9x 16 y 45 0

9.25x2 9y2 50x 27 y 65 0

10.x2 x 49 y 65 0

11.49x2 4y2 98x 44y 95 0

12.16x2 16y2 32x 48y 54 0

13.49x2 36y2 147x 72y 651 0

14.4x2 81y2 80x 324y 562 0

15.9x2 4y2 81x 160y 52 0

16.25x2 36y2 75x 72y 68 0

17.16x2 25y2 32x 150y 72 0

18.9x2 49y2 90x 98y 100 0

19.x2 4y2 8x 12y 48 0

20.49x2 4y2 196x 120y 94 0

21.16x2 4y2 64x 40y 124 0

68

22.25x2 9y2 75x 180y 149 0

23.36x2 25y2 72x 400y 452 0

24.4y2 3x 16y 45 0

25.25x2 9y2 100x 270y 65 0

4.В задачах даны координаты вершин пирамиды АВСD (таблица 6). Найти: 1) длину АВ; 2) угол φ между векторами АВ и АС;3) площадь грани AВС; 4) объем пирамиды; 5) длину высоты DH пирамиды, проведенной к плоскости грани АВС. Записать уравнения: 6) прямой АВ; 7) плоскости АВС; 8) высоты пирамиды DH; 9) высоты АК треугольника АВС,

Таблица 6 – Данные к заданию 4.

№ задания	А	В	С	D
1	(-2;3;-2)	(2;-3;2)	(2;2;0)	(1;5;5)
2	(1;0;8)	(-2;4;5)	(0;3;8)	(1;2;-5)
3	(4;-3;-2)	(2;2;3)	(2;-2;-3)	(-1;-2;13)
4	(5;1;0)	(7;0;1)	(2;1;4)	(5;5;3)
5	(4;2;-1)	(3;0;4)	(0;0;4)	(5;-1;-3)
6	(0;0;2)	(2;0;5)	(1;1;0)	(4;1;2)
7	(-1;2;3)	(3;0;5)	(2;-1;4)	(7;3;0)
8	(1;2;0)	(4;1;2)	(0;0;2)	(3;0;5)
9	(4;1;2)	(1;1;0)	(3;0;5)	(0;0;2)
10	(0;2;3)	(-1;4;2)	(7;3;7)	(2;5;0)
11	(1;5;5)	(-4;3;-2)	(2;-3;2)	(2;2;0)
12	(1;3;3)	(1;-1;1)	(0;2;4)	(4;2;-3)
13	(1;-1;2)	(2;1;1)	(1;1;4)	(3;6;4)
14	(1;-3;2)	(5;1;-4)	(2;0;3)	(1;-5;2)
15	(4;2;-1)	(3;0;4)	(0;0;4)	(5;-1;3)
16	(-1;3;-1)	(3;-2;3)	(3;3;-3)	(2;0;4)
17	(1;-2;4)	(6;-1;4)	(4;3;8)	(3;-4;10)
18	(2;-3;2)	(-2;3;-2)	(-2;-2;0)	(-1;-5;-5)
19	(-3;3;3)	(6;-1;4)	(0;8;7)	(-1;1;9)
20	(-4;-2;1)	(-3;0;-4)	(0;0;-4)	(-5;1;3)
		69